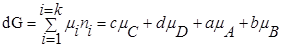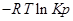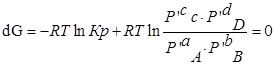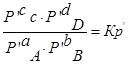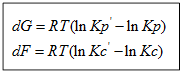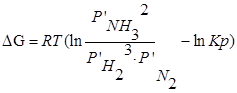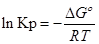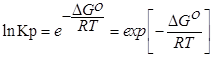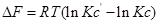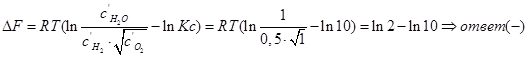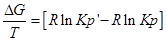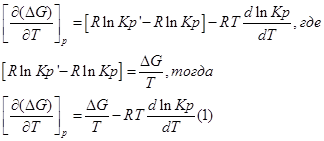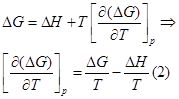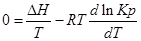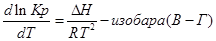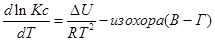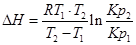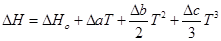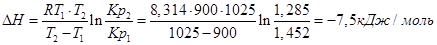Уравнение изобары вант гоффа зависимость

Константа равновесия определяют условия равновесия, когда концентрация (парциальные давления) является равновесными. В каком направлении пойдёт химическая реакция, если парциальное давление исходных веществ и продуктов реакции отличаются от равновесных? Ответить на этот вопрос поможет уравнение изотермы химической реакции.

Рассмотрим уравнение реакции: aA + bB ↔ cC + dD

Для изобарно-изотермического процесса изменение Гиббса равно:

P’- неравновесное, парциальное давление компонентов.

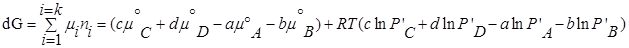
где =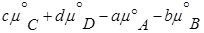

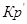
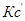
— по форме записи напоминает константу равновесия, но отличается тем, что вместо равновесных давлений в него входят величины давления в данный момент времени.

( ) — это выражение, куда входят величины концентраций в данный момент времени.

АНАЛИЗ ИЗОТЕРМЫ ВАНТ-ГОФФА

1. Главное значение изотермы реакции состоит в том, что она позволяет рассчитать ∆Gили ∆Fобратимый реакции для заданного состава реакционной смеси и определить, в каком направлении, и до какого предела протекает реакция при известных условиях.

а) Если Кр˃Кр’, то lnКр˃lnКр’; ∆G˂0- реакция идет самопроизвольно в прямом направлении.

б) Если Кр˂Кр’, то lnКр˂lnКр’; ∆G˃0- реакция протекает самопроизвольно в обратном направлении, в сторону образования продуктов.

в) Если Кр=Кр’, то lnКр=lnКр’; ∆G=0- равновесие.

Если парциальное давление всех участников реакции в данный момент времени равны атмосферному давлению

Пусть P_A’=P_B’=P_C’=P_D’=1( 1,013*10 5 Па), тоKp’=1; Тогда логарифм этого выражения будет равен нулю (lnKp’=0), а уравнение изотермы Вант – Гоффа примет вид:

∆G⁰=RTlnKp-стандартная энергия Гиббса

Выразм константу равновесия из последнего уравнения и получим:

Пример решения задачи:

В объеме 10л, взяли: 320(г) О₂ , 10(г) Н₂ и 180(г) паров воды . Определите, в какую направлении пойдёт химическая реакция: 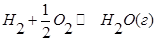, если при температуре Т

(Кс=10). Процесс изохорный.

;

;

;

;

;

;

˂0 — реакция идет в прямом направлении.

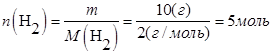
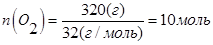
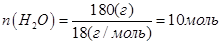
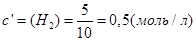
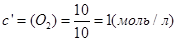
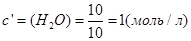
ВЛИЯНИЕ ВНЕШНИХ УСЛОВИЙ НА КОНСТАНТУ

РАВНОВЕСИЯ. УРАВНЕНИЕ ИЗОБАРЫ И ИЗОХОРЫ ВАНТ-ГОФФА (В-Г)

Константы равновесия — это величины постоянные при данной температуре. При изменении температуры константа равновесия изменяется, и довольно существенно.

Изменение константы равновесия и направления химической реакции в зависимости от температуры количественно характеризует уравнение изобары изохоры химической реакции.

ВЫВОД УРАВНЕНИЯ ИЗОБАРЫ И ИЗОХОРЫ

Разделим уравнение изотермы Вант- Гоффа на температуру:

Продифференцируем его по Т и перепишем:

Представим уравнение Гиббса – Гельмгольца в виде:

Из уравнения (1) вычтем уравнение (2):

Эти уравнения показывают влияния температуры на константу равновесия, где определяющим фактором является тепловой эффект химической реакции.

Влияние температуры на константу равновесия определяется типом реакци.

1. Если тепловой эффект реакци ∆H(∆U)˃0(эндотермическая, поглощение), то 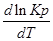˃0, тогда при увеличении температуры (Т↑) константа равновесия Кр увеличивается.

В обратном — Т↓,Кр↓.

2. Если ∆H(∆U)˂0 (экзотермическая, выделение), то 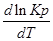˂0, тогда при повышении температуры константа равновесия Кр уменьшается или Кр увеличивается при понижении температуры.

В обратном — Т↑,Кр↓.

3. Если ∆H(∆U)=0 , тов этом случае константа равновесия не зависит от температуры Кp ≠ f(T).

ИНТЕГРИРОВАНИЕ ИЗОБАРЫ В-Г

1. Приближенное интегрирование ∆Н ≠ f(Т),

тогда ;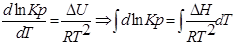

;

;

;

;

.

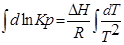
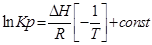
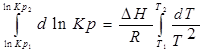
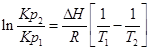
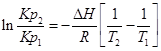
С помощью этого уравнения можно найти:

1. ∆Н (тепловой эффект реакции), если известны равновесия при двух различных температурах (Кр₁(Т₁) и Кр₂(Т₂))

2. Кр₂(Т₂) – константу равновесия при температуре Т_2, если известна константа равновесия при другой температуре и тепловой эффект реакции (Кр₁(Т₁) и ∆Н).

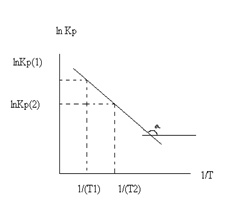
Так как после интегрирования мы получили уравнение прямой, то эта зависимость может быть представлена на графике: lnKp(1) lnKp(2)

Тангенс угла наклона прямой реакции, исходя из уравнения прямой:

;.

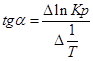
Зависимость теплового эффекта от температуры выражается уравнением:

Подставим это уравнение в уравнение изобары Вант- Гоффа:

;

при Т=0(К)

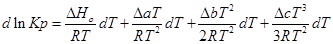
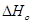
Проинтегрируем это уравнение и получим:

;

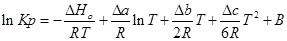
где В — постоянная интегрирования, для нахождения необходимо знать значения константы равновесия Кр при любой фиксированной температуре.

Однако проводить расчеты с использованием данного уравнения довольно сложно и используется довольно редко.

Пример. Определим изменение эффекта реакции Fe+H₂O+FeO+H₂, если для Т₁=900К, Кр₁=1,452, а для Т₂=1025К Кр₂=1,285.

Используем уравнение:

При повышении температуры от 900 до 1025К выделится дополнительно 7,5 кДж/моль теплоты.

Дата добавления: 2016-02-02 ; просмотров: 9755 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Решение задач на тему: "Правило Вант-Гоффа". 1 часть. 10 класс.Скачать

Уравнение изобары вант гоффа зависимость

ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ

Конспект лекций для студентов биофака ЮФУ (РГУ)

1.7 ХИМИЧЕСКОЕ РАВНОВЕСИЕ

Как было показано выше, протекание самопроизвольного процесса в термодинамической системе сопровождается уменьшением свободной энергии системы (dG 2 Y > 0. Таким образом, условием термодинамического равновесия в закрытой системе является минимальное значение соответствующего термодинамического потенциала :

Изобарно-изотермические (P = const, T = const):

Изохорно-изотермические (V = const, T = const):

Состояние системы с минимальной свободной энергией есть состояние термодинамического равновесия:

Термодинамическим равновесием называется такое термодинамическое состояние системы, которое при постоянстве внешних условий не изменяется во времени, причем эта неизменяемость не обусловлена каким-либо внешним процессом.

Учение о равновесных состояниях – один из разделов термодинамики. Далее мы будем рассматривать частный случай термодинамического равновесного состояния – химическое равновесие. Как известно, многие химические реакции являются обратимыми, т.е. могут одновременно протекать в обоих направлениях – прямом и обратном. Если проводить обратимую реакцию в закрытой системе, то через некоторое время система придет в состояние химического равновесия – концентрации всех реагирующих веществ перестанут изменяться во времени. Необходимо отметить, что достижение системой состояния равновесия не означает прекращения процесса; химическое равновесие является динамическим, т.е. соответствует одновременному протеканию процесса в противоположных направлениях с одинаковой скоростью. Химическое равновесие является подвижным – всякое бесконечно малое внешнее воздействие на равновесную систему вызывает бесконечно малое изменение состояния системы; по прекращении внешнего воздействия система возвращается в исходное состояние. Ещё одним важным свойством химического равновесия является то, что система может самопроизвольно прийти в состояние равновесия с двух противоположных сторон. Иначе говоря, любое состояние, смежное с равновесным, является менее устойчивым, и переход в него из состояния равновесия всегда связан с необходимостью затраты работы извне.

Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации С, парциальные давления P или мольные доли X реагирующих веществ. Для некоторой реакции

соответствующие константы равновесия выражаются следующим образом:

(I.78) (I.79)

(I.80)

Константа равновесия есть характерная величина для каждой обратимой химической реакции; величина константы равновесия зависит только от природы реагирующих веществ и температуры. Выражение для константы равновесия для элементарной обратимой реакции может быть выведено из кинетических представлений.

Рассмотрим процесс установления равновесия в системе, в которой в начальный момент времени присутствуют только исходные вещества А и В. Скорость прямой реакции V₁ в этот момент максимальна, а скорость обратной V₂ равна нулю:

(I.81)

(I.82)

По мере уменьшения концентрации исходных веществ растет концентрация продуктов реакции; соответственно, скорость прямой реакции уменьшается, скорость обратной реакции увеличивается. Очевидно, что через некоторое время скорости прямой и обратной реакции сравняются, после чего концентрации реагирующих веществ перестанут изменяться, т.е. установится химическое равновесие.

Приняв, что V₁ = V₂, можно записать:

(I.83)

(I.84)

Т.о., константа равновесия есть отношение констант скорости прямой и обратной реакции. Отсюда вытекает физический смысл константы равновесия: она показывает, во сколько раз скорость прямой реакции больше скорости обратной при данной температуре и концентрациях всех реагирующих веществ, равных 1 моль/л.

Теперь рассмотрим (с некоторыми упрощениями) более строгий термодинамический вывод выражения для константы равновесия. Для этого необходимо ввести понятие химический потенциал . Очевидно, что величина свободной энергии системы будет зависеть как от внешних условий (T, P или V), так и от природы и количества веществ, составляющих систему. В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы. Введем в некоторую систему бесконечно малое количество dn_i молей i-го компонента; это вызовет бесконечно малое изменение термодинамического потенциала системы. Отношение бесконечно малого изменения величины свободной энергии системы к бесконечно малому количеству компонента, внесенному в систему, есть химический потенциал μ _i данного компонента в системе:

(I.85)

(I.86)

Химический потенциал компонента связан с его парциальным давлением или концентрацией следующими соотношениями:

(I.87)

(I.88)

Здесь μ°_i – стандартный химический потенциал компонента (P_i = 1 атм., С_i = 1 моль/л.). Очевидно, что изменение свободной энергии системы можно связать с изменением состава системы следующим образом:

(I.89)

(I.90)

Поскольку условием равновесия является минимум свободной энергии системы (dG = 0, dF = 0), можно записать:

(I.91)

В закрытой системе изменение числа молей одного компонента сопровождается эквивалентным изменением числа молей остальных компонентов; т.е., для приведенной выше химической реакции имеет место соотношение:

(I.92)

Отсюда можно получить следующее условие химического равновесия в закрытой системе:

(I.93)

В общем виде условие химического равновесия можно записать следующим образом:

(I.94)

Выражение (I.94) носит название уравнения Гиббса – Дюгема. Подставив в него зависимость химического потенциала от концентрации, получаем:

(I.95)

(I.96)

Для изобарно-изотермического процесса аналогичным образом можно получить:

(I.97)

Полученные нами выражения I.96 – I.97 есть изотерма химической реакции . Если система находится в состоянии химического равновесия, то изменение термодинамического потенциала равно нулю; получаем:

(I.98)

(I.99)

Здесь с_i и р_i – равновесные концентрации и парциальные давления исходных веществ и продуктов реакции (в отличие от неравновесных С_i и Р_i в уравнениях I.96 – I.97).

Поскольку для каждой химической реакции стандартное изменение термодинамического потенциала ΔF° и ΔG° есть строго определенная величина, то произведение равновесных парциальных давлений (концентраций), возведенных в степень, равную стехиометрическому коэффициенту при данном веществе в уравнении химической реакции (стехиометрические коэффициенты при исходных веществах принято считать отрицательными) есть некоторая константа, называемая константой равновесия. Уравнения (I.98, I.99) показывают связь константы равновесия со стандартным изменением свободной энергии в ходе реакции. Уравнение изотермы химической реакции связывает величины реальных концентраций (давлений) реагентов в системе, стандартного изменения термодинамического потенциала в ходе реакции и изменения термодинамического потенциала при переходе из данного состояния системы в равновесное. Знак ΔG (ΔF) определяет возможность самопроизвольного протекания процесса в системе. При этом ΔG° (ΔF°) равно изменению свободной энергии системы при переходе из стандартного состояния (P_i = 1 атм., С_i = 1 моль/л) в равновесное. Уравнение изотермы химической реакции позволяет рассчитать величину ΔG (ΔF) при переходе из любого состояния системы в равновесное, т.е. ответить на вопрос, будет ли химическая реакция протекать самопроизвольно при данных концентрациях С_i (давлениях Р_i) реагентов:

(I.100)

(I.101)

Если изменение термодинамического потенциала меньше нуля, процесс в данных условиях будет протекать самопроизвольно.

1.7.1 Влияние внешних условий на химическое равновесие

При постоянстве внешних условий система может находиться в состоянии равновесия сколь угодно долго. Если изменить эти условия (т.е. оказать на систему какое-либо внешнее воздействие), равновесие нарушается; в системе возникает самопроизвольный процесс, который продолжается до тех пор, пока система опять не достигнет состояния равновесия (уже при новых условиях). Рассмотрим, как влияют на положение равновесия некоторые факторы.

1.7.2 Влияние давления и концентрации

Рассмотрим несколько возможных случаев смещения равновесия.

1. В систему добавлено исходное вещество. В этом случае

; ;

По уравнению изотермы химической реакции (I.100 – I.101) получаем: ΔF 0; ΔG > 0. Химическое равновесие будет смещено влево (в сторону расходования продуктов реакции и образования исходных веществ).

3. Изменено общее давление (для реакций в газовой фазе).

Парциальные давления всех компонентов Р_i в этом случае изменяются в одинаковой степени; направление смещения равновесия будет определяться суммой стехиометрических коэффициентов Δn.

Учитывая, что парциальное давление газа в смеси равно общему давлению, умноженному на мольную долю компонента в смеси (Р_i = РХ_i), изотерму реакции можно переписать в следующем виде (здесь Δn = Σ(n_i) _прод – Σ(n_i) _исх):

(I.102)

(I.103)

Примем, что Р₂ > Р₁. В этом случае, если Δn > 0 (реакция идет с увеличением числа молей газообразных веществ), то ΔG > 0; равновесие смещается влево. Если реакция идет с уменьшением числа молей газообразных веществ (Δn изобару Вант-Гоффа :

(I.06)

Рассуждая аналогичным образом, для процесса, проходящего в изохорных условиях, можно получить изохору Вант-Гоффа :

(I.107)

Изобара и изохора Вант-Гоффа связывают изменение константы химического равновесия с тепловым эффектом реакции в изобарных и изохорных условиях соответственно. Очевидно, что чем больше по абсолютной величине тепловой эффект химической реакции, тем сильнее влияет температура на величину константы равновесия. Если реакция не сопровождается тепловым эффектом, то константа равновесия не зависит от температуры.

Экзотермические реакции: ΔH° 0 (ΔU° > 0). В этом случае температурный коэффициент логарифма константы равновесия положителен; повышение температуры увеличивает величину константы равновесия (смещает равновесие вправо).

Графики зависимостей константы равновесия от температуры для экзотермических и эндотермических реакций приведены на рис. I.4.

Рис. 1.4 Зависимость константы равновесия от температуры.

Действие рассмотренных нами факторов (давления, концентрации и температуры), равно как и любых других, на систему, находящуюся в состоянии равновесия, обобщает принцип смещения равновесия , называемый также принципом Ле Шателье – Брауна :

Если на систему, находящуюся в состоянии истинного равновесия, оказывается внешнее воздействие, то в системе возникает самопроизвольный процесс, компенсирующий данное воздействие.

Принцип Ле Шателье – Брауна является одним из следствий второго начала термодинамики и применим к любым макроскопическим системам, находящимся в состоянии истинного равновесия.

Copyright © С. И. Левченков, 1996 — 2005.

Видео:Химическое равновесие. Закон действующих масс.Скачать

Уравнение изобары вант гоффа зависимость

Химическим равновесием называется такое состояние обратимой химической реакции

при котором с течением времени не происходит изменения концентраций реагирующих веществ в реакционной смеси. Состояние химического равновесия характеризуется константой химического равновесия:

, (9.1)

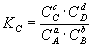
где C_i – концентрации компонентов в равновесной идеальной смеси.

Константа равновесия может быть выражена также через равновесные мольные доли X_i компонентов:

. (9.2)

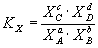
Для реакций, протекающих в газовой фазе, константу равновесия удобно выражать через равновесные парциальные давления P_i компонентов:

. (9.3)

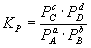
Константа равновесия связана с _rG o химической реакции:

(9.5)

(9.6)

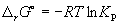
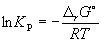
Изменение _rG или _rF в химической реакции при заданных (не обязательно равновесных) парциальных давлениях P_i или концентрациях C_i компонентов можно рассчитать по уравнению изотермы химической реакции (изотермы Вант-Гоффа):

. (9.7)

. (9.8)

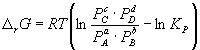
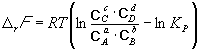
Согласно принципу Ле Шателье, если на систему, находящуюся в равновесии, оказать внешнее воздействие, то равновесие сместится так, чтобы уменьшить эффект внешнего воздействия. Так, повышение давления сдвигает равновесие в сторону уменьшения количества молекул газа. Добавление в равновесную смесь какого-либо компонента реакции сдвигает равновесие в сторону уменьшения количества этого компонента. Повышение (или понижение) температуры сдвигает равновесие в сторону реакции, протекающей с поглощением (выделением) теплоты.

Количественно зависимость константы равновесия от температуры описывается уравнением изобары химической реакции (изобары Вант-Гоффа)

(9.9)

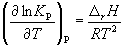
и изохоры химической реакции (изохоры Вант-Гоффа)

. (9.10)

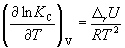
Интегрирование уравнения (9.9) в предположении, что _rH реакции не зависит от температуры (что справедливо в узких интервалах температур), дает:

(9.11)

(9.12)

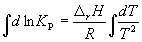
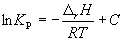
где C – константа интегрирования. Таким образом, зависимость ln K_P от 1/Т должна быть линейной, а наклон прямой равен – _rH /R.

(9.13)

(9.14)

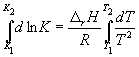
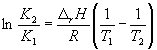
По этому уравнению, зная константы равновесия при двух разных температурах, можно рассчитать _rH реакции. Соответственно, зная _rH реакции и константу равновесия при одной температуре, можно рассчитать константу равновесия при другой температуре.

ПРИМЕРЫ

Пример 9-1. Рассчитать константу равновесия для реакции

при 500 K. _fG o для CO(г) и CH₃OH(г) при 500 К равны –155.41 кДж . моль –1 и –134.20 кДж . моль –1 соответственно.

Решение. G o реакции:

_rG o = _fG o (CH₃OH) – _fG o (CO) = –134.20 – (–155.41) = 21.21 кДж . моль –1 .

= 6.09 10 –3 .

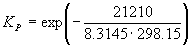
Пример 9-2. Константа равновесия реакции

равна K_P = 1.64 10 –4 при 400 o C. Какое общее давление необходимо приложить к эквимолярной смеси N₂ и H₂, чтобы 10% N₂ превратилось в NH₃? Газы считать идеальными.

Решение. Пусть прореагировало моль N₂. Тогда

0

N2(г)	+	3H2(г)	=	2NH3(г)
Исходное количество	1	1
Равновесное количество	1–	1–3	2 (Всего: 2–2 )
Равновесная мольная доля: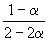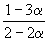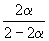

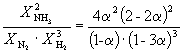
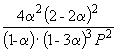
Следовательно, K_X = и K_P = K_{X .} P –2 = .

Подставляя = 0.1 в полученную формулу, имеем

1.64 10 –4 =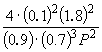, откуда P = 51.2 атм.

Пример 9-3. Константа равновесия реакции

при 500 K равна K_P = 6.09 10 –3 . Реакционная смесь, состоящая из 1 моль CO, 2 моль H₂ и 1 моль инертного газа (N₂) нагрета до 500 K и общего давления 100 атм. Рассчитать состав равновесной смеси.

Решение. Пусть прореагировало моль CO. Тогда

CO(г)	+	2H2(г)	=	CH3OH(г)
Исходное количество:	1	2	0
Равновесное количество:	1–	2–2
Всего в равновесной смеси:	3–2 моль компонентов + 1 моль N2 = 4–2 моль
Равновесная мольная доля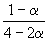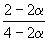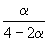

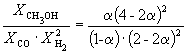
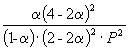
Следовательно, K_X = и K_P = K_{X .} P –2 = .

Таким образом, 6.09 10 –3 = .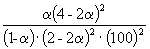

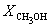
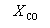
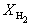
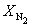
Решая это уравнение, получаем = 0.732. Соответственно, мольные доли веществ в равновесной смеси равны: = 0.288, = 0.106, = 0.212 и = 0.394.

Пример 9-4. Для реакции

при 298 К K_P = 6.0 10 5 , а _fH o (NH₃) = –46.1 кДж . моль –1 . Оценить значение константы равновесия при 500 К.

Решение. Стандартная мольная энтальпия реакции равна

_rH o = 2 _fH o (NH₃) = –92.2 кДж . моль –1 .

Согласно уравнению (9.14), =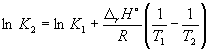

= ln (6.0 10 5 ) + 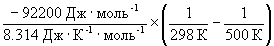= –1.73, откуда K₂ = 0.18.

Отметим, что константа равновесия экзотермической реакции уменьшается с ростом температуры, что соответствует принципу Ле Шателье.

ЗАДАЧИ

Указание: во всех задачах считать газы идеальными.

При 1273 К и общем давлении 30 атм в равновесной смеси

содержится 17% (по объему) CO₂. Сколько процентов CO₂ будет содержаться в газе при общем давлении 20 атм? При каком давлении в газе будет содержаться 25% CO₂?

При 2000 o C и общем давлении 1 атм 2% воды диссоциировано на водород и кислород. Рассчитать константу равновесия реакции

Константа равновесия реакции

при 500 o C равна K_p = 5.5. Смесь, состоящая из 1 моль CO и 5 моль H₂O, нагрели до этой температуры. Рассчитать мольную долю H₂O в равновесной смеси.

Константа равновесия реакции

при 25 o C равна K_p = 0.143. Рассчитать давление, которое установится в сосуде объемом 1 л, в который поместили 1 г N₂O₄ при этой температуре.

Сосуд объемом 3 л, содержащий 1.79 10 –2 моль I₂, нагрели до 973 K. Давление в сосуде при равновесии оказалось равно 0.49 атм. Считая газы идеальными, рассчитать константу равновесия при 973 K для реакции

при 250 o C _rG o = –2508 Дж . моль –1 . При каком общем давлении степень превращения PCl₅ в PCl₃ и Cl₂ при 250 o C составит 30%?

константа равновесия K_P = 1.83 10 –2 при 698.6 К. Сколько граммов HI образуется при нагревании до этой температуры 10 г I₂ и 0.2 г H₂ в трехлитровом сосуде? Чему равны парциальные давления H₂, I₂ и HI?

Сосуд объемом 1 л, содержащий 0.341 моль PCl₅ и 0.233 моль N₂, нагрели до 250 o C. Общее давление в сосуде при равновесии оказалось равно 29.33 атм. Считая все газы идеальными, рассчитать константу равновесия при 250 o C для протекающей в сосуде реакции

Константа равновесия реакции

при 500 K равна K_P = 6.09 10 –3 . Рассчитать общее давление, необходимое для получения метанола с 90% выходом, если CO и H₂ взяты в соотношении 1: 2.

ln K = –1.04 –1088 /T +1.51 10 5 /T 2 .

Рассчитать _rG o , _rH o и _rS o реакции при 400 К.

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

📺 Видео

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Задачи на правило Вант-Гоффа. Зависимость скорости реакции от температуры.Скачать

Использование правила Вант-Гоффа для решения зада. Химия для поступающих.Скачать

Правило Вант-Гоффа для ЕНТ по химии 2023 | Химия ЕНТ УмскулСкачать

Химическое равновесие. Константа равновесия. 10 класс.Скачать

Закон Вант-ГОФФАСкачать

Влияние температуры на скорость реакцииСкачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Осмос и осмотическое давлениеСкачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать

124. Правило Вант-Гоффа. Решение задач.Скачать

83. Химическое равновесиеСкачать

Свободная энергия Гиббса. 10 класс.Скачать

Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать

Влияние температуры на скорость химических реакцийСкачать

Вывод уравнения неразрывности - Лекция 1Скачать

Закон разбавления ОствальдаСкачать

задачи на коллигативные свойстваСкачать