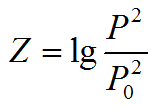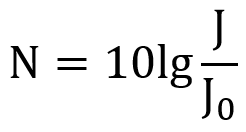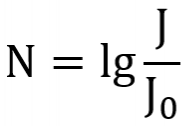Звуковым полем называется пространство, в котором распространяется звуковая волна.
Основный характеристикой звукового поля является звуковое давление Р, интенсивность звука J (сила звука).
Интенсивность звука измеряется в (вт/м 2 ).
Связь между силой звука и звуковым давлением вычисляется по формуле:
Интенсивность звука находится по формуле:
Р — звуковое давление, Па;
с —скорость распространения звука в среде, м/с;
ρ0 — плотность среды распространения звука, кг/м 3 .
Уровень звукового давления вычисляется по формуле:
P — звуковое давление в точке измерения, Па;
P0 — звуковое давление на пороге слышимости и равна 2·10 -5 , Па;
Уровень интенсивности звука N в децибелах определяется по формуле (используется десятичный логарифм):
J — интенсивность звука в точке измерения (уровень вычисляется), Вт/м;
J0 — интенсивность звука при частоте 1000 Гц (порог слышимости), примерно равен 1·10 -12 вт/м.
Уровень интенсивности звука измеряется в децибелах (дц).
Логарифмическая шкала выражает частоты от 0 до 140 дц.
Как видно, выражение подчинено логарифмическому закону, то есть, если интенсивность звука увеличить в сто раз, то ощущение громкости увеличится всего лишь в 2 раза.
Уровень интенсивности звука в неперах вычисляется по формуле (используется натуральный логарифм):
Здесь, интенсивность звука измеряется в неперах, 1 непер равен 8,7 дб.
Видео:Давление звукового излученияСкачать

Уровни звукового давления и интенсивности.
Поскольку человеческий слух различает огромный диапазон изменения звукового давления (разница между самым тихим звуком 2∙10 -5 Па и самым громким звуком 20 Па составляет 10 6 ), то использовать при измерениях такую большую шкалу чрезвычайно неудобно, поэтому во всех измерительных приборах (шумомерах, измерительных компьютерных станциях и др.) используется логарифмическая шкала, которая позволяет сжать масштаб измерения звукового давления.
Для этого используется уровень звукового давления, который определяется как:
Уровень звукового давления измеряется в децибелах (дБ).
Например, если звуковое давление равно 2 Па, то уровень звукового давления равен:
Lp = 20 lg p/p0 = 20 lg (2 Па / (2∙10 -5 ) Па) = 20 lg (1 ∙ 10 +5 ) = 20∙5 = 100 дБ.
Обратный пример: если задан уровень звукового давления Lp = 80 дБ, то звуковое давление определяется следующим образом:
Lp = 20 lg p/p0, отсюда 80 дБ = 20 lg p / (2∙10 -5 ), значит, lg p/(2∙10 -5 ) = 4. Следовательно, 10 4 = p/(2∙10 -5 ), отсюда значение звукового давления будет равно p = 0,2 Па.
Увеличение звукового давления в два раза соответствует изменению уровня звукового давления на 6 дБ. Например, звуковое давление 2 Па соответствует уровню звукового давления 100 дБ, а звуковое давление 1 Па соответствует уровню 94 дБ, звуковое давление 4 Па – уровню 106 дБ и т.д.
Кроме того, следует обратить внимание на то, что уровни звукового давления нескольких одновременно работающих различных источников никогда не складываются. Для определения суммарного уровня необходимо рассчитать значения звукового давления, соответствующего каждому уровню: p1 и p2. Затем определить суммарное звуковое давление 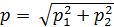
Например, если играют скрипка с уровнем 80 дБ и рояль с уровнем 86 дБ, то их суммарный уровень звукового давления определяется следующим образом. Уровню 80 дБ соответствует звуковое давление 0,2 дБ, уровню 86 дБ – звуковое давление 0,4 Па. Суммарное давление равно: p = 0,447 Па, отсюда скрипка и рояль вместе создают уровень звукового давления 86,98 дБ.
При оценке слухового восприятия звуковых колебаний, кроме звукового давления, часто используют и другую величину — интенсивность или силузвука. Громкость звука зависит от его интенсивности, которая, в свою очередь, зависит от звукового давления, создаваемого источником звука в точке прослушивания.
Интенсивность I и звуковое давление р связаны соотношением:
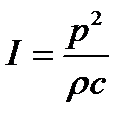
где ρ – плотность воздуха, равная 1,2 кГ/м 3 ;
с – скорость распространения звуковых колебаний в воздухе, равная при температуре 20°С 343 м/с.
Из практики хорошо известно, что чем больший уровень звукового давления создаёт источник звука, тем громче он звучит. Однако одного только уровня звукового давления для характеристики громкости звучания недостаточно, поскольку чувствительность человеческого слуха различна для различных частот. По этой причине для его определения пользуются графиком, который наглядно показывает, как изменяется минимальное значение звукового давления, воспринимаемого человеческими органами слуха как звук, в зависимости от частоты акустических колебаний. Такой график называется кривой абсолютного порога слышимости (рис. 13.2). Определяется он в полосе частот от 20 до 20000 Гц – именно в этом диапазоне человеческий слух способен воспринимать акустические колебания как звук. Однако следует иметь в виду, что такая широкая полоса слышимых частот скорее физиологический предел возможностей человеческого слуха – в действительности подавляющее большинство людей даже в молодом возрасте (18-25 лет), когда острота слуха наивысшая, способно слышать звуки только в диапазоне 30-35…16000-18000 Гц. Тем не менее, есть данные, что отдельные люди способны слышать звуки даже с частотой 22000 Гц.
Порог слышимости – это минимальное значение звукового давления, при котором еще наблюдается слуховое ощущение. Он характеризует чувствительность слуха к интенсивности звуковой энергии.
| 31,5 Гц |
| 63 Гц |
| 125 Гц |
| 250 Гц |
| 500 Гц |
| 1 кГц |
| 2 кГц |
| 4 кГц |
| 8 кГц |
| 16 кГц |
| f |
| -20 |
| Lp, дБ |
| Рис. 13.2. Кривая абсолютного порога слышимости, построенная по результатам измерений в условиях свободного поля |
Абсолютный порог слышимости принято выражать в децибелах по отношению к некоторой стандартной величине звукового давления р1 = 2×10 -5 Па (10 -12 Вт/м 2 ), которая условно принята за точку отсчета (0 дБ) при таких оценках. Как видно из рис. 13.2, наибольшей чувствительностью человеческий слух обладает на средних частотах — в диапазоне от 2000 до 5000 Гц. Здесь абсолютный порог слышимости даже меньше 2×10 -5 Па (
Если создать три тональных звуковых сигнала с одним и тем же уровнем звукового давления p = 40 дБ – один с частотой 50 Гц, другой с частотой 100 Гц, третий с частотой 4 кГц и попытаться сравнить их громкости, то окажется, что сигнал с частотой 4 кГц будет звучать достаточно громко, сигнал с частотой 100 Гц – едва слышно, а вот сигнала с частотой 50 Гц не удастся услышать вовсе. Если обратиться к рис. 13.2, то причина будет ясна – сигнал с частотой 50 Гц при уровне звукового давления 40 дБ будет находиться ниже кривой абсолютного порога слышимости, сигнал с частотой 100 Гц лишь немного выше нее, и только сигнал с частотой 4 кГц будет более чем на 40 дБ превышать абсолютный порог слышимости. Этот эксперимент доказывает, что громкость зависит не только от интенсивности звука, но и от его частоты. На краях диапазона слышимых частот можно сформировать звуковые сигналы очень высокой интенсивности, но никакого ощущения громкости при этом не возникнет, хотя слуховая система при этом может быть даже повреждена.
Построение шкалы звуков по громкости и исследование влияния на нее основных параметров звукового сигнала было выполнено, прежде всего, на тональных сигналах различной интенсивности, частоты и длительности. Для того чтобы устранить зависимость субъективно воспринимаемой громкости звука от частоты и обеспечить возможность количественной ее оценки, используют метод сравнения громкости исследуемого звука с громкостью некоторого эталонного звука. Для того чтобы такие оценки можно было сравнивать между собой, на международном уровне договорились использовать в качестве эталона громкость звукового сигнала с частотой 1000 Гц.
Определяется громкость следующим образом. На эталонной частоте 1000 Гц устанавливается некоторый вполне определенный уровень звукового давления, например 40 дБ. После этого эксперту предлагается прослушать сигнал на какой-то другой частоте, например 63 Гц, и отрегулировать его уровень таким образом, чтобы он казался равногромким эталонному. Значение уровня звукового давления эталонного сигнала в децибелах при этом квалифицируется как уровень громкости исследуемого сигнала и оценивается в специальных единицах, которые называются фонами.
Видео:Что такое ДЕЦИБЕЛ #5. Звук. Громкость звука. Давление звука. Сила звука.Скачать

Звуковое давление и его уровни (spl)
В настоящее статье поговорим о том, что такое звуковое давление, рассмотрим понятие (импеданс) — удельное акустическое сопротивление среды. Также поговорим об уровнях звукового давления и интенсивности звука.
Чтобы лучше понимать о чём сегодня пойдёт речь, советую прочитать предыдущую статью по этой теме ( звуковые волны, виды, длина волны и скорость звука ).
Видео:Сила звукового давления ● 1Скачать

Звуковое давление
Звуковая волна, как мы уже рассматривали в прошлой статье, распространяется в среде в виде волн сжатия и разряжения плотности.
В газах (в том числе и воздухе) плотность и давление связаны между собой:
p = RTp
А поскольку у волны имеются области сжатия и разряжения, то в первой области давление будут выше статического атмосферного. А в случае разряжения – ниже.
Вот как это выглядит:
Разность между мгновенным значением давления в данной точке среды и атмосферным давлением называется звуковым давлением.
Звуковое давление измеряется в паскалях (Па): 1 Па = 1 Н/м².
Наша слуховая система может определять очень большой диапазон разностей между мгновенным значением звукового давления и атмосферным.
На рисунке ниже представлено, различное звуковое давление от звуковых источников в децибелах (про децибелы подробнее читай далее):
Видео:Диск РэлеяСкачать

Импеданс
Рассматривая звук, в прошлой статье ( читать ) мы выяснили, что звуковая волна зависит от частоты и амплитуды звукового давления. Если тело оказывает большое сопротивление приложенному звуковому давлению, то частицы приобретают малую скорость.
Поэтому импеданс – это удельное акустическое сопротивление среды. Представляет из себя отношение звукового давления к скорости колебаний частиц среды:
Z = p/v
Измеряется в (Па · с)/м или кг/(с · м²).
Удельное акустическое сопротивление для воздуха составляет (при температуре 20 С°) 413 кг/(с · м²). В металле, к примеру, оно составляет 47,7 × 10 кг/(с · м²). Так как в воздухе импеданс достаточно мал, то и излучаемая полезная энергия также мала.
Если рассматривать КПД (коэффициент полезного действия) музыкальных инструментов, голосового аппарата, громкоговорителей и т. п., то оно в воздухе находится в пределах 0,2-1%.
Энергетические параметры
Звуковая волна переносит энергию механических колебаний, значит она имеет энергетические параметры. Среди которых: акустическая энергия P (Дж); мощность W – энергия, переносимая в единицу времени (Вт); интенсивность I – количество энергии, проходящее в единицу времени через единицу площади, перпендикулярной к направлению распространения волны (Вт/м²); плотность – количество звуковой энергии в единице объёма (Дж/м²).
Уровни звукового давления (анг. SPL, sound pressure level)
Восприятие громкости человеком происходит не по линейному закону, пропорционально амплитуде колебаний, а по логарифмическому. Поэтому для определения параметров звука применяют логарифмические шкалы.
Человек различает огромный диапазон изменения звукового давления от тихого 2 × 10 ⁻⁵ Па до очень громкого 20 Па. Разница составляет 10⁶.
Использовать такую школу очень неудобно. Поэтому в измерительных приборах пользуются логарифмическими единицами – децибелами (дБ). Эта единица происходит от другой – бел, который равен десятикратному изменению интенсивности звука. Однако бел – единица крупная и неудобная для измерений. Поэтому применяется её десятая часть – децибел.
Уровень звукового давления определяется как:
L = 20 lg p/p₀
Например, если звуковое давление p = 2 Па, то уровень звукового давления равен: L = 20 lg (2 Па/(2 × 10 ⁻⁵) Па) = 20 lg (1 × 10⁺⁵) = 20 × 5 = 100 дБ.
Один децибел – примерно та наименьшая разница в громкости, которую человеческое ухо может почувствовать.
Полезно запомнить следующее. Изменение громкости в 3 дБ равно отношению 2:1. Поэтому если мы берем два одинаковых источника звука, т. е. удваиваем мощность, то громкость увеличиться на 3 дБ. Например, если к голосу присоединяется ещё один, равный по громкости, то уровень звука увеличится на 3 дБ. Если нужно ещё увеличить на 3 дБ, потребуется вдвое увеличить имеющийся состав.
Также можно обратиться к следующей таблице (в ней показано на сколько дБ нужно убавить, чтобы получить звучание в 2 раза тише, в 3 и т. д.):
| 1% | 10% | 25% | 33% | 50% | 100% |
| 1/100 (в 100 раз тише) | 1/10 (в 10 раз тише) | 1/4 (в 4 раза тише) | 1/3 (в 3 раза тише) | 1/2 (в 2 раза тише) | 1/1 |
| -40дБ | -20дБ | -12 дБ | -10 дБ | — 6 дБ | 0 дБ |
Для определения суммарного уровня давления нескольких инструментов их никогда не складывают. Вначале необходимо рассчитать значение звукового давления каждого инструмента. Допустим играют две скрипки. Одна с уровнем 80 дБ, другая 86 дБ. У первой звуковое давление равно — 0,2 Па, второй — 0,4 Па.
Рассчитывается так: L = 20 lg p/p₀, значит 80 дБ = 20 lg p / (2 × 10 ⁻⁵), далее lg p / (2 × 10 ⁻⁵) = 4. Следовательно 10⁴ = p / (2 × 10 ⁻⁵), отсюда значение звукового давления будет p = 0,2 Па.
После этого определяется суммарное звуковое давление
В нашем случае суммарное давление равно p = 0, 447 Па. Затем определяется суммарный уровень звукового давления. Который равен 86,98 дБ.
Уровень интенсивности звука
Уровень интенсивности звука также измеряется в децибелах по формуле:
L₁ = 10 lg I/I₀
I₀ – нулевой уровень, равный 10⁻¹² Вт/м².
Мощность, напряжение, ток
Перечисленные электрические характеристики также часто приводятся в децибелах и имеют свои специальные обозначения. Приведём несколько примеров:
L dBm = 10 lg WВт/ 1мВт – уровень мощности отнесённый к 1 мВт
L dBv = 20 lg UB/1B – уровень напряжения, отнесённый к 1 В (Америка)
L dBv = 20 lg UB/0,775 B – уровень напряжения, отнесённый к 0,775 В (Европа)
Спасибо, что читаете New Style Sound ( подписаться на новости )
🌟 Видео
Что такое ДЕЦИБЕЛЫ на самом деле?Скачать

Уровень звукового давления в реальном миреСкачать

Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать

КАК устроен ЗВУК: Децибелы, Ватты и ЧастотыСкачать

Урок 96 (осн). Характеристики звука: высота, громкость, тембрСкачать

Урок 377. Звук и его характеристикиСкачать

Громкость звукаСкачать

Звук, характеристики звука, акустический резонанс, эхо. Практическая часть - решение задачи.9 класс.Скачать

Урок 95 (осн). Механические волны. ЗвукСкачать

Сила звукового давления ● 2Скачать

Закон БернуллиСкачать

Физические основы акустики, Центрнаучфильм, 1980Скачать

Сила звукового давления ● 3Скачать

Распространение звука. Звуковые волны | Физика 9 класс #32 | ИнфоурокСкачать

Высота, тембр и громкость звука | Физика 9 класс #31 | ИнфоурокСкачать

Амплитуда, период, частота и длина волны периодических волнСкачать