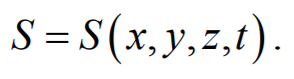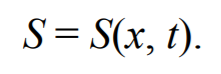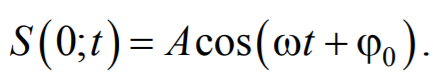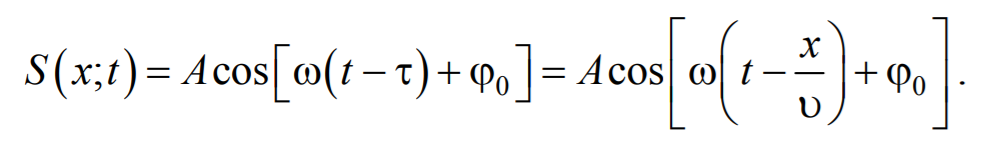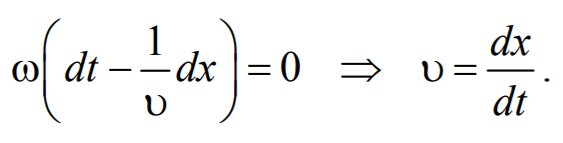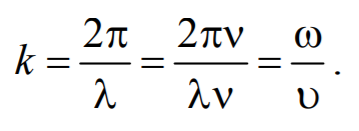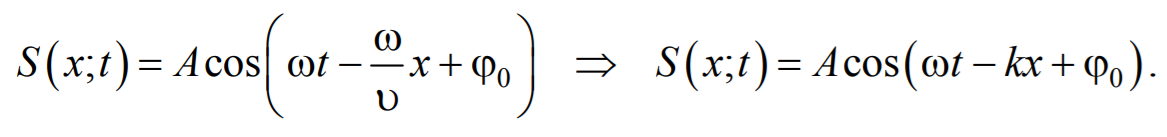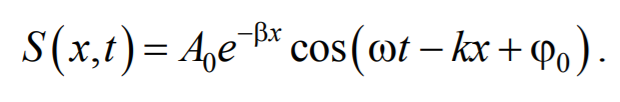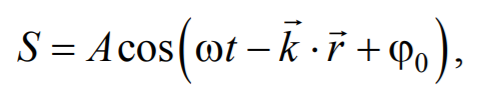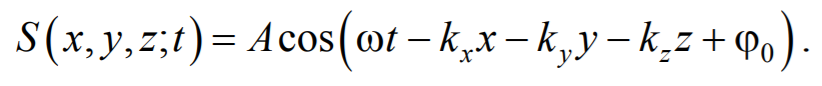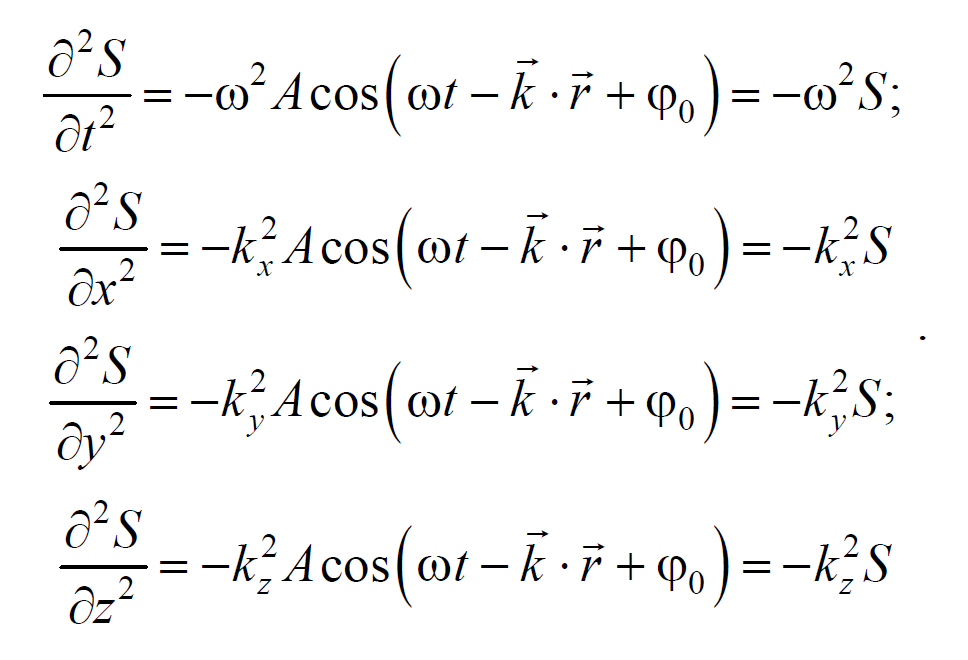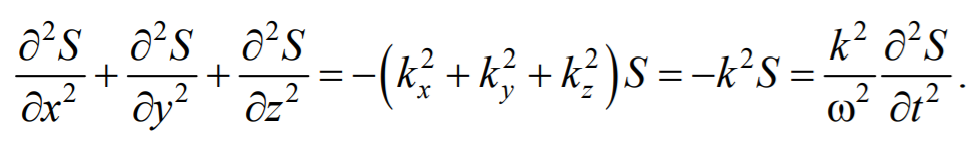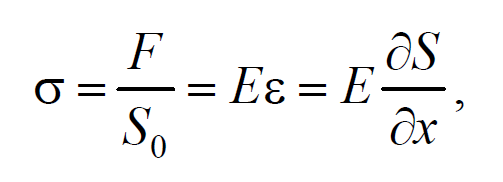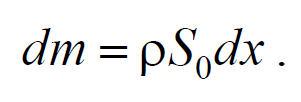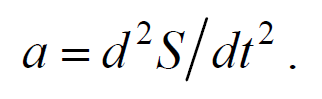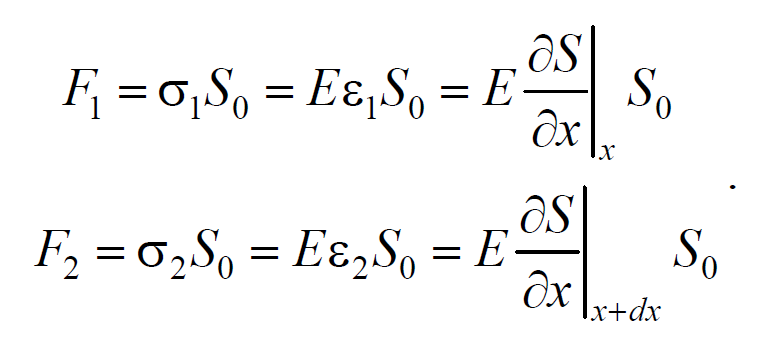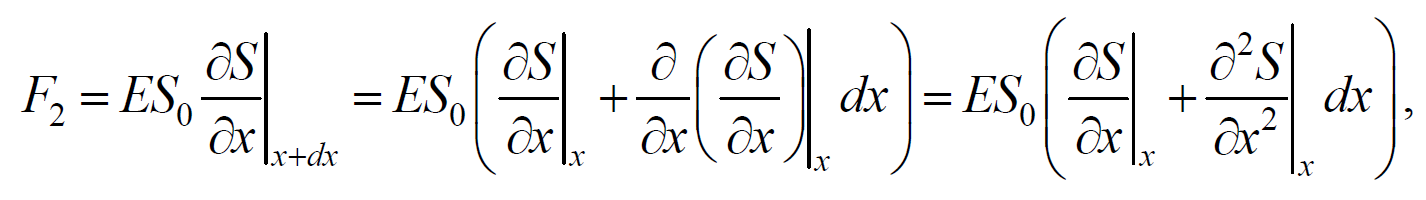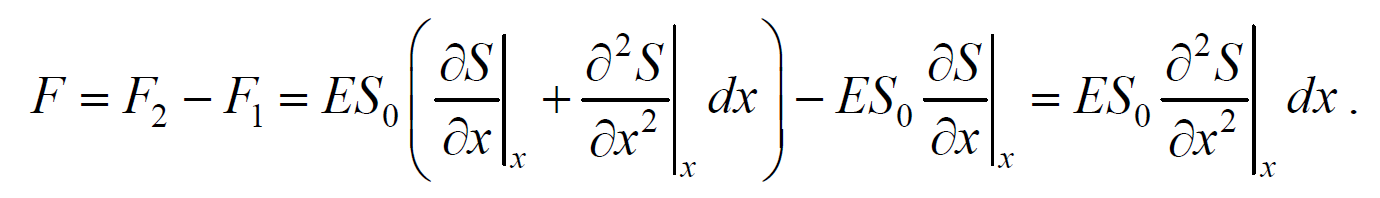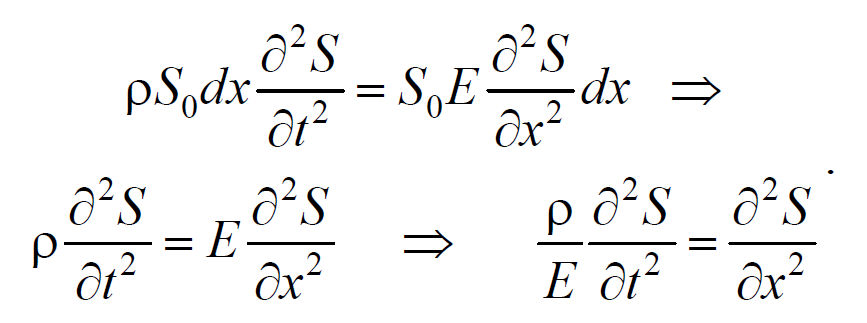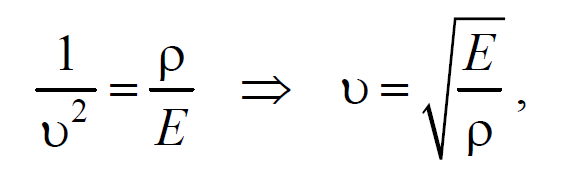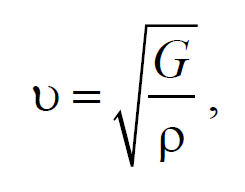Уравнение и график плоской волны (2 видео)

Уравнение и график плоской волны

отстоящие друг от друга на расстоянии λ, колеблются одинаковым образом.

Уравнение плоской волны

Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер.

Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0)

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е.

— это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой.

Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z.

В общем виде уравнение плоской волны записывается так:

Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде.

Введем волновое число k = 2π/λ, или в векторной форме

где k — волновой вектор; n — нормаль к волновой поверхности.

Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k.

Тогда уравнение плоской волны запишется так:

Содержание

Лекция №9. Механические волны
6.1. Распространение колебаний в упругой среде
6.2. Уравнение плоской волны
6.3. Волновое уравнение
6.4. Скорость распространения волн в различных средах
Уравнение и график плоской волны
📹 Видео

Видео:Получение уравнения плоской бегущей волны.Скачать

Лекция №9. Механические волны

6.1. Распространение колебаний в упругой среде

Механические колебания, распространяющиеся в упругой среде (твердой, жидкой или газообразной), называются механическими или упругими волнами .

Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение. Они лишь совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества .

В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.

Упругая волна называется продольной , если колебания частиц среды происходят в направлении распространения волны. Продольные волны связаны с объемной деформацией растяжения − сжатия среды, поэтому они могут распространяться как в твердых телах, так и в жидкостях и газообразных средах.

Упругая волна называется поперечной , если колебания частиц среды происходят в плоскостях, перпендикулярных к направлению распространения волны Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела.

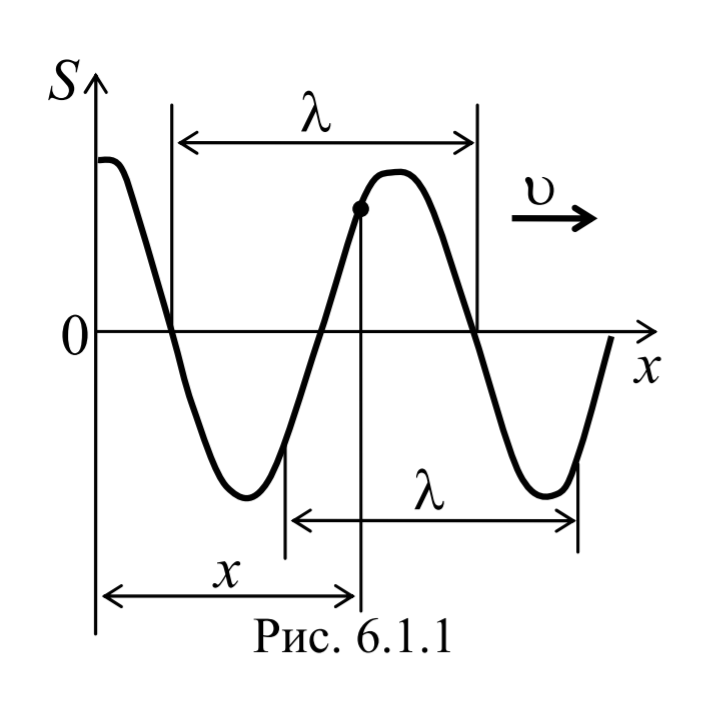
На рис. 6.1.1 представлена гармоническая поперечная волна, распространяющаяся вдоль оси 0х . График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны также равна тому расстоянию, на которое распространяется определенная фаза колебания за период колебаний

Колеблются не только частицы, расположенные вдоль оси 0х , а совокупность частиц, заключенных в некотором объеме. Геометрическое место точек, до которых доходят колебания к моменту времени t , называется фронтом волны . Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, а в сферической − множество концентрических сфер.

6.2. Уравнение плоской волны

Уравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x , y , z и времени t

Эта функция должна быть периодической как относительно времени t , так и относительно координат x , y , z . Периодичность по времени вытекает из того, что смещение S описывает колебания частицы с координатами x , y , z , а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.

Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t

Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х . Пусть колебания точек, лежащих в плоскости х = 0 имеют вид

Найдем вид колебания точек в плоскости, соответствующей произвольному значению х . Для того, чтобы пройти путь от плоскости х = 0 до плоскости х , волне требуется время τ = x/υ . Следовательно, колебания частиц, лежащих в плоскости х , будут отставать по времени на τ от колебаний частиц в плоскости х = 0 и описываться уравнением

где А − амплитуда волны; ϕ₀ − начальная фаза волны (определяется выбором начал отсчета х и t ).

Зафиксируем какое-либо значение фазы ω(t-x/υ)+ϕ₀=const. Это выражение определяет связь между временем t и тем местом х , в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим

Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью .

При υ > 0 волна распространяется в сторону возрастания х . Волна, распространяющаяся в противоположном направлении, описывается уравнением

Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину $$k = $$ , которая называется волновым числом , которое можно представить в виде

Тогда уравнение плоской волны будет иметь вид

Мы предполагали, что амплитуда колебаний не зависит от х . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону A=A₀e −βx . Тогда уравнение плоской волны для поглощающей среды имеет вид

6.3. Волновое уравнение

Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид

где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности

Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.

Перейдем от радиус-вектора точки к ее координатам x , y , z 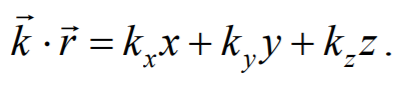Тогда уравнение (6.3.2) примет вид

Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)

Сложив производные по координатам, и с учетом производной по времени, получим

6.4. Скорость распространения волн в различных средах

Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х . Выделим в среде цилиндрический объем с площадью основания S₀ и высотой d_x . Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S , то смещение основания с координатой x+dx будет S+dS . Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию ε=∂S/∂x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения σ , которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия

где Е − модуль Юнга среды.

Из зависимости смещения от координаты x видно, что относительная деформация ∂S/∂x , а также, и напряжение σ в фиксированный момент времени зависят от х . В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.

Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема

где ρ − плотность недеформированной среды.

Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным

Тогда этот участок объема будет растянут под влиянием сил F₁ и F₂ , приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно

После разложения силы F₂ в ряд, получим

и результирующая F₁ , F₂ сил, действующая на элемент объема равна

Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим

Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) $$=$$ , получим

где Е − модуль Юнга.

Полученное уравнение определяет фазовую скорость продольных упругих волн.

Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид

Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Уравнение и график плоской волны

В общем случае процесс распространения волны в среде описывается дифференциальным уравнением второго порядка в частных производных – т.н. волновым уравнением. Данное уравнение устанавливает в дифференциальной форме зависимость между смещением s точки, ее координатой x и временем t при условии, что волны распространяются вдоль оси OX без затухания так, что амплитуды колебаний всех точек одинаковы и равны А.

Одномерное волновое уравнение имеет вид:

(4.7),

где V – скорость распространения волны.

Решение этого дифференциального уравнения позволяет получить зависимость, называемую уравнением плоской волны, смещения s колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения x и времени t, т.е. s=f(x,t)

(4.8)

График волны внешне похож на график гармонического колебания, но по существу они различны. График колебания представляет зависимость смещения данной частицы от времени, т.е. s=f(t) при x=const.

График волны представляет зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени т.е.s=f(x) при t=const. Он является как бы «моментальной фотографией» волны.

Эффект Доплера.

Эффектом Доплера называется изменение частоты колебания (или длины волны), воспринимаемой наблюдателем, при движении источника колебаний и наблюдателя друг относительно друга. Допустим, наблюдатель движется по направлению к источнику, испускающему импульсы (волны) с постоянной частотой n. Однако благодаря сложению направленных навстречу друг другу скоростей испущенных волн V_и и наблюдателя V_н, с точки зрения этого наблюдателя соседние волны будут разделены меньшим промежутком времени. Поэтому ему будет казаться, что волны имеют большую частоту (или меньшую длину волны), чем в действительности. И наоборот, если наблюдатель будет удаляться от источника волн, то частота с точки зрения наблюдателя будет меньше, а длина волны – больше. Запишем общую формулу для величины воспринимаемой частоты n ¢:

(4.9)

В этой формуле верхние знаки относятся к случаю сближения источника и наблюдателя, и нижние – к случаю их взаимного удаления.

Применительно к звуковым частотам эффект Доплера хорошо заметен для человеческого восприятия: звук сирены быстро приближающегося автомобиля или локомотива кажется нам более высоким (высокочастотным), когда же источник звука проследовал мимо нас и начал удаляться, звук кажется нам заметно более басовым, низким (низкочастотным).

Эффект Доплера используется для определения скорости движения тела в среде, в том числе в медицинских исследованиях – например, для определения скорости движения клапанов и стенок сердца (доплеровская эхокардиография), других органов, скорости кровотока. Если источник ультразвука излучает волны с частотой n_и в неподвижную среду, в которой со скоростью V₀ движется исследуемый объект, то этим объектом (как наблюдателем) частота этих волн воспринимается измененной вследствие эффекта Доплера. Затем волна отражается объектом в направлении неподвижного приемника, который также воспринимает уже другую частоту – таким образом, получается разница частот, называемая доплеровским сдвигом частоты

(4.10)

где V – скорость движения ультразвука в данной среде. В исследованиях, проводимых в медицине, эта скорость значительно выше скорости движения исследуемых объектов, что позволяет использовать следующую формулу:

(4.11)

Аналогичным образом этот метод можно применять для обнаружения движения грудной клетки зародыша, дистанционного контроля за сердцебиением плода. Следует заметить, что эффект Доплера лежит в основе метода обнаружения с помощью радара превышения скорости автомобилями (в этом случае используются радиоволны, а не механические волны). Эффект Доплера характерен для волн любой природы.

Глава 5. Акустика.

Вопросы

Основные понятия акустики.

Физические характеристики звука.

Характеристики слухового ощущения.

Звуковые методы исследования в медицине.

Ультразвук, инфразвук. Применение в медицине.

Основные понятия акустики.

Акустика –область физики, изучающая колебания и волны в упругойсреде. Часто под акустикой понимают учение о звуке. При изучении звука можно выделить три основных аспекта: должен существовать источник звука, причем, как и для любой механической волны, источником звуковой волны являются колебания тела; энергия переносится от источника звука в виде продольных звуковых волн;звук регистрируется (воспринимается) нашим ухом или прибором.

Звук – это упругие колебания и волны с частотами от 16 до 20000 Гц

(20 кГц), которые воспринимаются органами слуха человека. С возрастом диапазон слышимости сужается, пожилые люди начинают хуже слышать высокие частоты, верхний предел их диапазона слышимости может понизиться до 10 кГц и даже ниже. Колебания с частотой ниже 16 Гц называются инфразвуком, с частотой больше 20 кГц–ультразвуком. В обоих случаях такие волны не воспринимаются человеком как слышимый звук, но они способны оказывать влияние на организм. Многие животные могут воспринимать ультразвуковые частоты, собаки могут слышать звуки частотой до 50 кГц, кошки и дельфины – до 100 кГц, летучие мыши – до 150 кГц.

По виду акустического спектра (акустическим спектром называют набор частот с указанием их относительной интенсивности) различают:

1) Музыкальные звуки, или тоны – звуки, являющиеся периодическими процессами. К ним относятся, например, гласные звуки речи. Если этот процесс – гармонический, то тон называется простым, или чистым. Основной характеристикой простого тона является частота. Если колебания негармонические (ангармонические), то тон называется сложным. Сложный тон может быть разложен на простые; наименьшая частота такого разложения называется частотой основного тона, остальные гармоники (обертоны) имеют частоты, кратные этой величине. Тон самой низкой частоты определяет общую высоту звука, обертоны определяют «окраску» (тембр) звука.

2) Шумы – звуки, отличающиеся сложной временной зависимостью; представляют собой сумму сложных тонов с беспорядочно изменяющимися амплитудами и частотами. К ним относятся согласные звуки речи, шум моря, множество техногенных звуков (образующихся при работе механизмов).

Для нормальной жизнедеятельности человека шум не должен превышать определенного порога. Так, для нормального сна и умственной деятельности шум не должен превышать 30 дБ; во многих учреждениях допускается шум до 55 дБ. Эти данные положены в основу санитарно-гигиенических акустических норм. Вредное воздействие производят лишь шумы, уровень интенсивности которых превосходит определенный предел. Слабые шумы природного происхождения не только не вредны, но даже благотворно влияют на психику человека.

Интенсивный шум прежде всего отрицательно сказывается на работе кортиева органа, приводя к повреждениям волосковых клеток. Причем первыми выходят из строя клетки, реагирующие на высокие частоты. Даже при кратковременном действии шума в 110 дБ временно снижается порог слуховой чувствительности на 10-15%. При длительном действии шума повреждения волосковых клеток становятся необратимыми. Однако действие шума не ограничивается нарушением работы слухового аппарата, поскольку слуховой анализатор через кору головного мозга влияет на работу других органов и систем, особенно на состояние нервной системы. Интенсивный шум вызывает изменения в циркуляции крови, возрастание СОЭ, нарушение работы органов внутренней секреции, сердечно-сосудистые заболевания.

3) Звуковые удары – кратковременные звуковые воздействия, например, в результате взрыва.

Звук по своей природе является механической волной. Фазовая скорость этих волн (называемая скоростью звука) зависит (при достаточно малых амплитудах) только от механических свойств среды и не зависит от частоты. Звуки распространяются в газах, жидкостях и твердых телах. Акустические волны в твердых телах могут быть поперечными и продольными; в жидкостях и газах, в которых отсутствуют деформации сдвига, возможны только продольные волны, представляющие собой чередующиеся области сгущений и разрежений.

Скорость продольных звуковых волн в твердом теле зависит от его плотности r и модуля упругости (модуля Юнга) E:

(5.1)

Скорость звука в жидкости зависит от плотности жидкости rи коэффициента сжимаемости жидкости K:

(5.2)

Скорость звука в твердых телах и жидкостях зависит также и от температуры, т.к. от температуры зависит плотность вещества.

Чередование процессов сжатия и разрежения в определенном объеме газа происходит столь быстро, что эти процессы можно считать адиабатическими.

Скорость звука в газах зависит в широких пределах от температуры и не зависит от давления газа:

(5.3)

где c — показатель адиабаты, R –универсальная газовая постоянная, Т—абсолютнаятемпература газа, М – молярная масса.

Скорость звука в воздухе при данной температуре с достаточной степенью точности можно определить по формуле:

где c₀ – скорость звука в воздухе при температуре 0 0 С, (c₀=331,6 м/с);t – температура воздуха (в градусах Цельсия). При повышении температуры на 1 0 С скорость звука в воздухе увеличивается примерно на 0,5 м/с. В твердых и жидких средах скорость звука значительно выше, например, в воде около 1500м/с. Эта скорость звука может быть принята как средняя и для мягких тканей тела человека.

При прохождении звуков через границу двух сред они могут отражаться и преломляться; законы отражения и преломления звука идентичны соответствующим законам для световых волн.

Важнейшей характеристикой среды, определяющей условия отражения и преломления, является волновое сопротивление z (удельный акустический импеданс), величина, равная произведению плотности среды r на скорость волны в среде:

Доля звуковой энергии, перешедшей из одной среды в другую, зависит от соотношения между величинами акустических сопротивлений обеих сред.

Коэффициентом отражения r называют отношение интенсивностей отраженной и падающей волн.

(5.6)

Коэффициентом проникновениязвуковой волны b через границу двух сред называют отношение интенсивностей прошедшей волны и падающей перпендикулярно на границу раздела сред:

(5.7)

Звуковая волна (при нормальном падении) пройдет границу раздела двух сред без отражения при равенстве волновых сопротивлений двух сред (b=1, r=0, если z₁=z₂,т.е. r₁ c₁ = r₂ c₂).Напротив, чем больше различаются между собой волновые сопротивления, тем меньшая доля звуковой энергии проникает через границу раздела. Можно подсчитать, что из воздуха в воду переходит всего 0,12% интенсивности падающего звука, а 99,88% отражается от границы раздела, т.е. происходит практически полное отражение.

При распространении звука (ультразвука) в среде его энергия убывает, т.е. происходит затухание волны, которое обусловлено не только поглощением, но и отражением звука от границы раздела, а также рассеянием на элементах микроструктуры вещества. Эти факторы особенно существенны при распространении звука в биологических объектах. При затухании звука, обусловленном рассеянием и поглощением, интенсивность звука убывает по экспоненциальному закону:

где I₀иI –соответственно интенсивности звука (ультразвука) на поверхности вещества и на расстоянии x от поверхности,d – коэффициент затухания, который в однородной среде равен:

В данной формуле l–длина волны звука; с – скорость звука в веществе; h –коэффициент вязкости и r – плотность вещества.

Как видно из формулы, коэффициент затухания уменьшается при увеличении длины волны. Поэтому звуки высокой частоты не распространяются в воздухе на далекие расстояния.

Если происходит только поглощение звука, то можно применить формулу

где m – коэффициент поглощения.

Ультразвук, имеющий малую длину волны, сильно поглощается в воздухе и меньше в жидкостях (плотность которых значительно больше плотности воздуха). В жидкостях с большой вязкостью поглощение ультразвука возрастает (что следует из формулы (5.9)). Существенно уменьшается интенсивность ультразвука при распространении его в биологических тканях, выполняющих в организме поддерживающую и опорную функции, из-за многочисленных отражений на волокнистых соединительных структурах. Этот факт иллюстрируют приведенные в таблице значения коэффициента затухания ультразвука частотой 1 МГц в различных тканях организма человека.