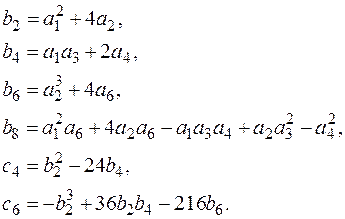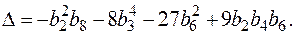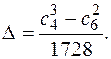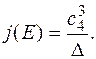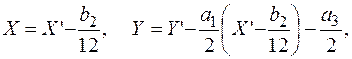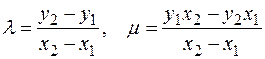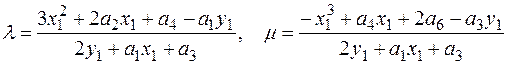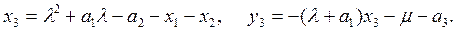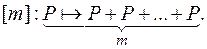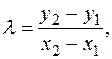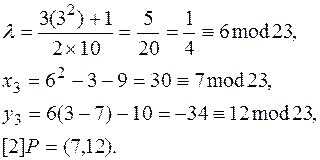Уравнение и график эллиптической кривой (8 видео)

Эллиптические кривые.

Проективная плоскость P 2 (K) над полем K определяется как множество троек (X, Y, Z) не равных одновременно нулю элементов X, Y, Z Î K, на котором введено отношение эквивалентности:

Так, например, две точки (4, 1, 1) и (5, 3, 3) эквивалентны в P 2 (F₇).

Класс эквивалентности троек называется проективной точкой.

Эллиптической кривой E называется множество точек проективной плоскости, удовлетворяющих однородному уравнению Вейерштрасса

Это уравнение называют также длинной формой Вейерштрасса. Кривая должна быть неособой в том смысле, что частные производные 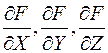не должны обращаться в нуль одновременно ни в одной ее точке.

Множество K-рациональных точек кривой E (то есть точек, удовлетворяющих уравнению кривой) обозначается через E(K).

Кривая имеет только одну точку, чья координата Z = 0, а именно (0, 1, 0). Ее принято называть бесконечно удаленной точкой (или точкой на бесконечности) и обозначать символом O.Для удобства часто пользуются аффинной версией уравнения Вейерштрасса:

K-рациональные точки в аффинном случае – это решения уравнения в K 2 и бесконечно удаленная точка O.

Переход от аффинных к проективным координатам:

— точка на бесконечности всегда переходит в бесконечно удаленную точку, как при переходе от аффинных координат к проективным, так и наоборот;

— проективная точка (X, Y, Z) кривой, отличная от бесконечно удаленной (Z ¹ 0), переходит в аффинную точку с координатами (X/Z, Y/Z);

— чтобы найти проективные координаты аффинной точки (X, Y), не лежащей на бесконечности, достаточно выбрать произвольное значение Z Î K * и вычислить (X·Z, Y·Z, Z).

Иногда удобнее пользоваться модифицированной формой проективной плоскости, когда проективные координаты (X, Y, Z) представляют аффинную точку (X/Z 2 , Y/Z 3 ).

Для эллиптической кривой вводятся следующие константы:

Дискриминант кривой E определяется по формуле

Если char K ¹ 2, 3, то дискриминант можно вычислить и так:

Деление на 1728 = 2 6 3 3 имеет смысл только в тех полях, чья характеристика отлична от 2 и от 3. Кривая E неособа тогда и только тогда, когда 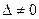. Далее рассматриваются только неособые кривые.

Для неособых кривых вводится j-инвариант

он тесно связан с понятием изоморфизма эллиптических кривых.

Говорят, что кривая E с координатами X и Y изоморфна над полем K кривой E’ с координатами X’, Y’ (обе заданы уравнением Вейерштрасса), если найдутся такие константы r, s, t Î K и u Î K * , что при замене переменных

кривая E перейдет в кривую E’. Отметим, что изоморфизм кривых определен относительно поля K. Изоморфизм эллиптических кривых является отношением эквивалентности.

Лемма. Изоморфные над полем K кривые имеют один и тот же j-инвариант. С другой стороны, любые кривые с совпадающими j-инвариантами изоморфны над алгебраическим замыканием 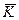поля K. То есть j-инвариант разделяет классы эквивалентности отношения изоморфизма над алгебраическим замыканием поля K.

Групповой закон

Рассмотрим для char K ¹ 2, 3 замену переменных

переводящую кривую заданную длинной формой Вейерштрасса в изоморфную ей кривую, определяемую короткой формой Вейерштрасса E: Y 2 = X 3 + aX + b при некоторых a, b Î K. На таких представителях классов изоморфных эллиптических кривых можно наглядно ввести групповой закон методом хорд и касательных.

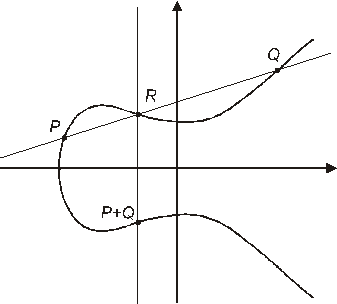
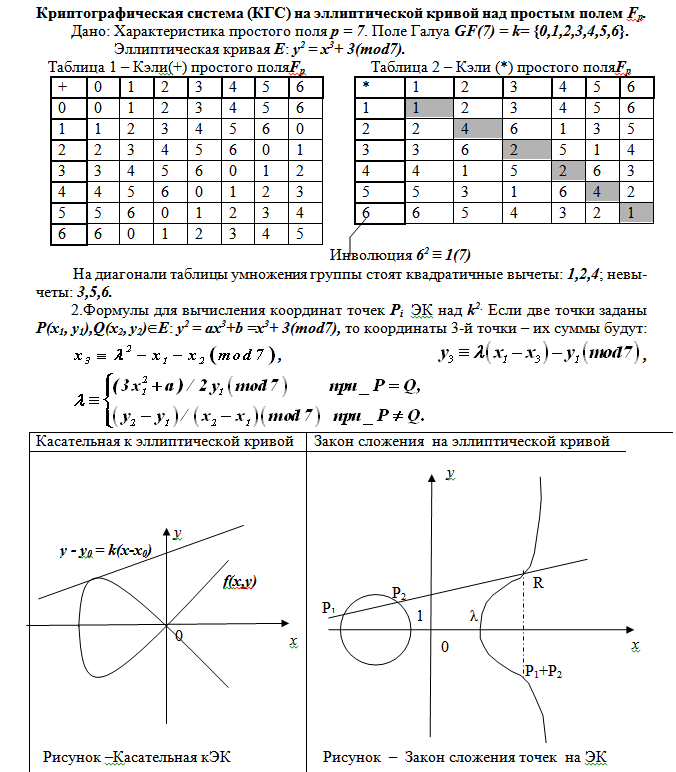
Сложение точек определяется с помощью хорд. Пусть P и Q – две точи кривой. Соединим их прямой линией. Она обязательно пересечет кривую в какой-то третьей точке R поскольку мы пересекаем кубическую кривую прямой. Точка R будет определена над тем же полем, что сама кривая и исходные точки P и Q. Отразим затем точку R относительно горизонтальной оси координат и получим точку, определяемую над основным полем. Последняя точка и будет суммой P + Q.

Рис.38. Групповой закон. Сложение точек.

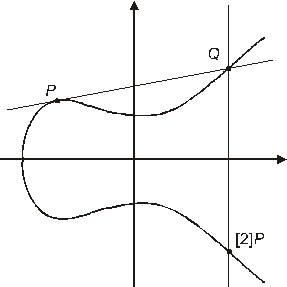
Касательные служат для удвоения точек (используя хорду нельзя сложить точку с собой). Пусть P – произвольная точка эллиптической кривой. Проведем касательную к кривой в точке P. Она пересечет кривую в какой-то третьей точке R (кубическая кривая пересекается по трем точкам с учетом кратности пересечения). Отразив R относительно горизонтальной оси, мы получим точку [2]P = P + P. Вертикальная касательная в точке P «пересекает» кривую в бесконечно удаленной точке. В этой ситуации P + P = O и говорят, что P – точка порядка 2.

Рис.39. Групповой закон. Удвоение точек.

Метод хорд и касательных наделяет эллиптическую кривую структурой абелевой группы с бесконечно удаленной точкой в качестве нейтрального (единичного) элемента, то есть нуля. Определение операций можно легко перенести на случай общей эллиптической кривой, заданной длинной формой Вейерштрасса (в частности характеристика поля может быть любой). Необходимо только заменить отражение относительно оси абсцисс на симметрию относительно прямой

Алгебраические формулы, реализующие сложение точек по методу хорд и касательных.

Лемма. Пусть E – эллиптическая кривая, определяемая уравнением

Фиксируем натуральное число m и обозначим через [m] отображение кривой на себя, сопоставляющее каждой точке P ее кратное [m]P, то есть

Это отображение – основа криптографических систем, опирающихся на эллиптическую кривую, поскольку его можно легко вычислить, но крайне сложно обратить, то есть по данным координатам P(x, y) и [m]P(x’, y’) найти m очень трудно. (Конечно сложность обращения предполагает специальный выбор эллиптической кривой и соблюдения других условий).

Дата добавления: 2016-02-13 ; просмотров: 2894 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Эллиптические кривые над конечными полями.
Факторизация и эллиптическая кривая. Часть III
Предварительные сведения из высшей алгебры
Элементы теории эллиптической кривой
Построение группы точек ЭК
Суммирование точек ЭК — групповая операция
Порядок группы и элемента группы
Метод факторизации числа, использующий эллиптическую кривую
Получение мультипликативного обратного элемента в кольце вычетов
Простая криптографическая система на эллиптических кривых
Заключение
💥 Видео

Видео:Как устроена эллиптическая криптография? Душкин объяснитСкачать

Эллиптические кривые над конечными полями.

Количество F_q-рациональных точек над эллиптической кривой конечно. Обозначим его #E(F_q). Ожидаемое число точек кривой близко к q + 1 и можно положить

где «дефект» t называется следом отображения Фробениуса в q.

Теорема Хассе. След отображения Фробениуса удовлетворяет неравенству

Есть два частных случая криптографически непригодных эллиптических кривых:

— Кривая E(F_q) называется аномальной, если ее след Фробениуса равен 1, тот есть

#E(F_q) = q. Эта кривая особенно неудобна, когда q – простое число.

— Кривая E(F_q) называется суперсингулярной, если характеристика p поля F_p делит след отображения Фробениуса t. Таких кривых также следует избегать в криптографии.

Выбирая кривую для шифрования, нужно стремиться к тому, чтобы число ее точек делилось на достаточно большое простое число. В связи с этим необходимо научиться вычислять порядок группы. Порядок произвольной группы E(F_q) над любым полем вычисляется за полиномиальное время.

Информация о порядке группы также существенна для оценки стойкости протокола, основанного на соответствующей кривой.

Одним из достоинств эллиптических кривых является то, что они доставляют большое число возможных групп. Можно менять как основное поле, так и коэффициенты уравнения кривой. Отыскать эллиптическую кривую с хорошими криптографическими свойствами для создания безопасного протокола достаточно легко.

Как правило реализация криптографичеких систем, основанных на эллиптической кривой, базируется на поле , чья характеристика равна 2, или на поле F_p с большим простым числом p.

Проективные координаты.

Одна из проблем, возникающих при использовании формул группового закона как при большой, так и при четной характеристике поля, связана с необходимостью деления. Деление в конечном поле считается дорогой операцией, так как включает в себя некий вариант расширенного алгоритма Евклида, который хотя и имеет приблизительно ту же сложность, что и умножение, однако обычно не может быть реализован достаточно эффективно.

Во избежание операции деления применяют проективные координаты. При этом уравнение кривой записывается через три координаты (X, Y, Z) вместо двух (X, Y). Однако вместо стандартного варианта уравнения кривой используется уравнение вида

Точка на бесконечности здесь также имеет координаты (0, 1, 0), но переход от аффинных координат к проективным осуществляется по правилу

выбор таких координат обусловлен стремлением сделать арифметические операции более эффективными.

Сжатие точек.

Во многих криптографических протоколах возникает необходимость хранить в памяти или передавать по сети отдельные точки эллиптической кривой. В аффинных координатах это можно сделать при помощи двух элементов поля: координат x и y. Однако экономнее применять так называемую технику сжатия точек.

Метод сжатия точек работает благодаря тому, что уравнение кривой в аффинных координатах при фиксированном значении x превращается в квадратно уравнение относительно координаты y. Значит, вместо двух координат для идентификации точки кривой можно хранить в памяти компьютера только координату x и еще некий двоичный параметр b, сообщающий о том, какое именно значение координаты y нужно брать.

Кривые над полем характеристикиp > 3

Пусть основное поле K = F_q с q = p n , где p > 3 – простое число и .

Уравнение кривой над таким полем можно представить в виде короткой формы Вейерштрасса

Ее дискриминант равен Δ = – 16(4a 3 + 27b 2 ), а j-инвариант – j(E) = – 1728(4a) 3 / Δ.

В проективных координатах формулы сложения точек эллиптической кривой, заданной уравнением

над полем характеристики p > 3 выглядят как

где тройка координат вычисляется последовательно по правилу:

здесь нет ни одной операции деления, кроме деления на 2, которое легко заменяется умножением на заранее вычисленное число 2 –1 (mod p).

Удвоение точек упрощается с помощью формул

Сжатие точек эллиптической кривой над полем характеристики p > 3.

Если p > 2, то квадратные корни ± β из элемента α Î F_p представляются натуральными числами разной четности из промежутка 1, …, p – 1, поскольку

Таким образом в качестве параметра b можно выбрать четность y координаты соответствующей точки. Полная информация о координатах точки по паре (x, b) осуществляется следующим образом. Сначала вычисляется

а затем переменной y присваивают значение β, если четность β совпадает с четностью b, и p – β, когда четности разные. Если же оказывается, что β = 0, то, не обращая внимания на параметр b, можно положить y = 0.

Не путать параметр четности b с коэффициентом кривой b.

Эллиптические группы.

Эллиптическая группа по модулю p определяется следующим образом. Выбираются два неотрицательных числа a и b, которые меньше p и удовлетворяют условию

4a 3 + 27b 2 (mod p) ¹ 0 (кривая не аномальная и не суперсингулярная).

Тогда E_p(a, b) обозначает эллиптическую группу по модулю p, элементами которой (x, y) являются пары неотрицательных целых чисел, которые меньше p и удовлетворяют условию

вместе с точкой в бесконечности O.

Пример.

p = 23. Рассмотрим эллиптическую кривую y 2 = x 3 + x + 1. В этом случае a = b = 1 и мы имеем 4 ´ 1 3 + 27 ´ 1 2 (mod 23) = 8 ¹ 0, что удовлетворяет условиям эллиптической группы по модулю 23.

Для эллиптической группы рассматриваются только целые значения от (0, 0) до (p, p) в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю p.

В общем случае список таких точек (см. табл.) составляется по следующим правилам.

1. Для каждого такого значения x, что , вычисляется x 3 + ax + b (mod p).

2. Для каждого из полученных на предыдущем шаге значений выясняется, имеет ли это значение квадратный корень по модулю p (вычисляется символ Лежандра). Если нет, то в E_p(a, b) нет точек с этим значением x. Если же корень существует, имеется два значения y, соответствующих операции извлечения квадратного корня (исключением является случай, когда единственным таким значением оказывается y = 0). Эти значения (x, y) и будут точками E_p(a, b).

Таблица 15. Точки на эллиптической кривой E₂₃(1, 1)

(0, 1)	(1, 7)	(3, 10)	(4, 0)	(5, 4)	(6, 4)	(7, 11)
(0, 22)	(1, 16)	(3, 13)	O	(5, 19)	(6, 19)	(7, 12)
(9, 7)	(11, 3)	(12, 4)	(13, 7)	(17, 3)	(18, 3)	(19, 5)
(9, 16)	(11, 20)	(12, 19)	(13, 16)	(17, 20)	(18, 20)	(19, 18)

Пример. Сложение и удвоение точек данной группы. P = (3, 10), Q = (9, 7).

Умножение определяется как повторное применение операции сложения

Видео:Эллиптическая криптография - Денис КовалевСкачать

Факторизация и эллиптическая кривая. Часть III

Использование эллиптических кривых (ЭК) для решения разнообразных задач криптологии коснулось каким-то боком и факторизации чисел . Здесь будем рассматривать вопрос, касающийся ЭК и не только в связи с проблемой факторизации составного нечетного натурального числа (СННЧ), но несколько шире.

Если пройтись по Интернету и по статьям об ЭК на Хабре, то после этого возникает мысль, что существует определенный пробел всех без исключения публикаций, включая и объемные бумажные книги. Авторы почему-то считают само-собой разумеющимся понимание природы ЭК и ее аддитивной группы, ее появление. На самом деле ЭК и ее группа (мое мнение) — это чудо!

Группа точек плоскости, множество которых замкнуто по операции сложения, оказалась каким-то образом встроена в ЭК и мы об этом до сего дня не знали бы, не располагая теорией групп, и даже при наличии теории групп, без гения Эйлера и Пуанкаре, которые нам эту группу открыли. В свое время Иоганн Кеплер открыл человеку законы движения Планет и качественно описал их траектории, но только гений Ньютона смог объяснить природу этих законов.

Правда для этого ему пришлось открыть свои законы движения/тяготения и изобрести дифференциальное и интегральное исчисления. Задача взятие двукратного интеграла от второго закона Ньютона, в котором ускорение — вторая производная пути, решением имеет плоскую кривую второго (не третьего, не путать эллипсы — траектории планет, спутников и эллиптические кривые в криптологии) порядка, что до И. Ньютона было открыто И.Кеплером.

Объект математики эллиптические кривые давно изучается геометрией(сама кривая, точки, касательные, ЭК, которая может быть изображена геометрическим рисунком, и др.) и алгеброй (уравнение ЭК, коэффициенты и корни уравнения, дискриминант, инварианты и др.). Но только в наш информационный век нашли важное практическое применение такому объекту.

Это применение связано с решением триединой задачи информационной безопасности. С обеспечением конфиденциальности, доступности и с контролем целостности. Такому важному применению способствовало открытие для рациональных (целых) точек ЭК свойства аддитивности (суммируемости), которое присуще и некоторым другим кривым, но в ЭК это свойство точек преобразует их множество в другой объект–алгебраическую аддитивную группу.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Предварительные сведения из высшей алгебры

Удобно теоретическое изложение материала построить в сопровождении конечного числового примера и детальных отступлений и комментариев, что позволит, не перескакивать по разным частям работы, и успешней вникать в существо излагаемого материала.

Вначале приведем кратко математические основы , без уяснения структур (группа, подгруппа, поле, подполе, кольцо, идеал, подкольцо) которых затруднено восприятие текста. Понятно, что задача не из простых (это передний край науки о числах) и требует от читателя определенной предварительной подготовки, но такова специфика «Хабра» — наличие читателей разного уровня подготовки.

Дадим несколько необходимых определений высшей алгебры.
Определение. Алгебраической (конечной) группой называется множество элементов (чисел, многочленов, матриц и др.) над которыми задана одна операция. В зависимости от природы элементов (матрицы, подстановки, вычеты по модулю N) операции могут различаться, но названия их, как правило, всегда одинаковы: сложение либо умножение. В случае групп вычетов по модулю N множество элементов группы может быть целыми или даже натуральными пополненными нулем числами от 0 до N — 1. Элементы группы отождествляются с номерами строк и столбцов таблицы Кели.

Эта единственная операция группы по назначению может быть сложением (+), и тогда группа называется аддитивной, или умножением (•), и группа — мультипликативная. Обеим операциям групп присущи близкие свойства (описываемые развернуто в учебной литературе): ассоциативность, замкнутость, наличие нейтрального и противоположного (обратного) элементов, а при сохранении результата операции в случае смены операндов местами — коммутативность.

Пример G.
Таблица Кели — Аддитивная группа вычетов по модулю N=23 (23 порядка)

В клетках таблицы суммы номеров строки и столбца по модулю N, пересекающихся в ней.

Таблица Кели — Мультипликативная группа вычетов по модулю N=23 (23 порядка)

В этой группе отсутствует нулевой элемент. Обратный мультипликативный элемент находят по этой таблице: вход номер строки и движемся по строке пока в некоторой позиции не встретим единицу; номер столбца клетки с единицей — обратный элемент к номеру строки. Например, для элемента 19 (строка 19) перемещаемся по строке до 17-го столбца, т.е. до клетки с 1. Номер столбца 17 и есть обратный элемент для 19-го. Действительно, их произведение по mod23 дает 19∙17(mod 23) =323(mod23) =1 единицу.

Поясним также свойство замкнутости операции в группе. Множество элементов, образующих конечную группу, конечно и постоянно. Результатами операции всегда являются элементы из исходного множества. Среди элементов группы только один-нейтральный элемент (1) или (0), и каждый элемент имеет себе обратный (а -1 ) (или противоположный (-а)). Операция над элементами не выводит результат за пределы исходного множества элементов группы.

Дело в том, что в группах вычетов по модулю N операции сложение или умножение не обычные, а модулярные, т. е. для группы задается число N, называемое модулем группы, и на него делятся все получаемые результаты. Такое деление, как правило, выполняется с остатком (придумано Гауссом) и именно остаток принимается за окончательный результат операции.

Определение. Алгебраическим числовым конечным простым полем вычетов по простому модулю N называется и обозначается множество (k, GF(p), Fp) элементов (чисел от 0 до N — 1), над которыми заданы две операции сложение (+) и умножение (•). Модуль N, по которому формируются элементы поля, должен быть обязательно простым числом.

Среди элементов обязательно имеются противоположные (-а) к каждому элементу и один нейтральный (0) по сложению, обратные (а -1 ) к каждому элементу и один нейтральный (1) по умножению. Поле образовано в соответствии с операциями допустимыми в нем (+) и (•) двумя соответствующими мультипликативной Fр* порядка р-1 и порядка р аддитивной группами.

Кроме конечных числовых простых полей в различных теориях (кодирования, криптографии, алгебре, геометрии и т. п.) используются расширенные поля многочленов степеней не выше n-1 по модулю неприводимого многочлена степени n.
Такие поля GF(p n ) появляются как результат расширения определенной степени n простых полей GF(p).

Определение. Расширенное поле К-поле GF(p n ), содержащее заданное поле GF(p) в качестве подполя, что записывают так К/k, где k = GF(p) — простое поле, К=GF(p n ) -расширение поля k. Элементами поля расширения K являются все элементы (числа) простого поля k и все многочлены степени не превышающей n-1. Иллюстрацией групп поля и результатов обеих операций в группах для примера поля GF(7) сложения и умножения являются числовые таблицы 1 и 2 помещенные в примерах ниже.

Пример P. Пусть задано конечное поле вычетов по модулю два — двоичное поле GF(2) = . Построим поле расширения степени, например, n = 6, что обозначается так GF(2 6 ). Это поле образуют числа 0, 1 и все возможные многочлены степени, не превышающей 5. Когда выполняются действия с многочленами в мультипликативной группе поля, то степень результата (произведения многочленов) degd(x) может превышать показатель степени n = 5.

При этом условие замкнутости множества элементов мультипликативной группы нарушается. Чтобы вернуть результат в поле — сделать его элементом поля, результат произведения делят на специально выбираемый многочлен (например, f(х) = х 6 + х + 1) степени равной степени расширения, т.е. n = 6. Окончательным результатом операции считается остаток от деления.

Такой многочлен в сущности формирует поле и не должен иметь корней в простом поле, он называется неприводимым многочленом, т. е. он не раскладывается на сомножители в поле. Действительно, при f(0) =0+0+1≠0 и f(1) =1+1+1(mod2) =1≠0, т.е. элементы 0 и 1 из GF(2) не являются корнями f(x). Говорят результаты операций расширенного поля приводятся по модулю неприводимого многочлена. Кроме того, все коэффициенты многочленов в этом поле принадлежат простому полю и приводятся по модулю простого поля (простого числа).

Таким образом, результаты операций в поле приводятся по двойному модулю, что иногда обозначается так d(х)(moddp,f(x)), где р — простое число, формирующее простое поле, а f(x) — неприводимый многочлен степени равной степени расширения простого поля.

). Неприводимый полином P(x) = x^6 + x +1 = 1000011, α = 2

Первая колонка таблицы поля Галуа GF(

) — степени примитивного элемента α=2, пробегающие все элементы поля, которые упорядочены по этим степеням. Вторая колонка — многочлены поля. Третья — векторное (двоичным числом ) представление элементов расширенного поля. Далее представление (

) десятичным числом, порядок (е) элемента, обратный вектор, степень обратного, обратный в десятичном представлении, вес элемента. Располагая такой таблицей поля, таблицы Кели не нужны.

Определение. Алгебраическим числовым конечным кольцом вычетов по составному модулю N (обозначается Z_N) называется множество элементов (чисел от 0 до N — 1), над которыми заданы две операции сложение (+) и умножение (•). Модуль N, по которому формируются элементы кольца должен быть составным (не простым) числом.

Если модуль сделать простым числом ( неприводимым многочленом ), то кольцо преобразуется в простое поле (поле многочленов ). Среди элементов кольца обязательно имеются противоположные (-а) к каждому элементу и нейтральный (0) по сложению, но обратный элемент (а -1 ) существует не для каждого элемента и нейтральный элемент (1) по умножению в кольце может отсутствовать.

Если модулем приведения является приводимый многочлен степени n, то возникает кольцо многочленов, элементами которого являются фактически те же самые элементы, что и в поле многочленов, но операции над многочленами выполняются уже не так как в поле расширения.

Аналогичная ситуация с элементами возникает и для векторных пространств — они там такие же как в поле и в кольце. Операции же существенно различны. Результаты операции умножения элементов поля и тех же элементов кольца или векторного пространства будут различаться. Для нашего изложения существенно то, что не все элементы имеют обратные в мультипликативной группе кольца.

Видео:ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ «НА ПАЛЬЦАХ»Скачать

Элементы теории эллиптической кривой

Моделирование многих явлений действительности, в частности, математических удобно выполнять с привлечением алгебраических структур: групп, полей, колец, алгебр и др. Те свойства, которые уже хорошо изучены для определенных структур, наследуются объектами, которые моделируются с использованием таких структур. Тем самым экономятся время и силы, а также и другие ресурсы.

Одним из примеров использования известных свойств конечных аддитивных групп является разработка алгоритмов решения задачи факторизации больших чисел (ЗФБЧ), другими алгоритмы цифровой подписи и/или шифрования документов (сообщений), в которых привлекаются не совсем обычные группы. В алгоритмах используются точки алгебраической кривой, заданной над конечными структурами (поле, кольцо), редуцированной (вычисления приводятся по модулю N) и называемой эллиптическая кривая в форме Вейерштрасса (1815-1897).

Целочисленные (рациональные) точки ЭК образуют аддитивную группу, т. е. их можно суммировать в любом порядке, получая при этом новые точки из этой группы. При определенных условиях, накладываемых на кривую, множество таких точек замкнуто и конечно, хотя порядок группы может быть очень большим.

Сама кривая плоская ее коэффициенты а и b; точки ЭК (х, у) описываются через две х и у переменные, значения которых принадлежат конечному простому полю Галуа GF(p) (но могут принадлежать и расширенному полю GF(p n ), как в некоторых стандартах электронной цифровой подписи (ЭЦП)), таким образом, в алгоритмах используется декартово произведение поля GF(p)×GF(p).

Операция сложения точек ЭК — это специальная операция (+), заключительный шаг которой взятие результата по модулю N простому или (для кольца) составному. При составном модуле ЭК задана не над полем, а над кольцом, что существенно изменяет свойства рассматриваемых объектов, сохраняя основные из них и существенные для целевой задачи.

Рассмотрим самые начальные сведения из теории и арифметики эллиптических кривых. Необходимо уяснить ряд моментов. Задание ЭК, смысловое значение параметров ЭК, множество целых точек и возможность их сложения между собой. Операция сложения точек. Эти сведения и их понимание необходимы для доступного изложения алгоритма факторизации натуральных (целых) чисел, который давно известен специалистам-криптологам по публикациям Х. Ленстра от 1987 г и более поздним усовершенствованиям Р. Монтгомери 1992 [2, 4, 5, 6, 7,10 ].

Для задания эллиптической кривой Е_a,b(F_р) над полем вначале задается поле характеристикой конечного поля — простым числом N или p>3. Для задания коэффициентов а и b эллиптической кривой Е (а, b), определенной над конечным простым полем Fр, можно воспользоваться подходом из отечественного стандарта ( см. ГОСТ ).

Определение. Эллиптической кривой Е_a,b(F_р) называется множество пар целых чисел, элементов поля х, у∊Fр, удовлетворяющих соотношению

После преобразований сравнения получается более простой вид

.
У Е_a,b(F_р) дискриминант многочлена правой части равен -4а 3 + 27b 2 ≢ 0(modp) и не сравним с нулем по модулю р и многочлен не имеет кратных корней Правильнее сказать так называется группа точек ЭК, а не сама кривая.

Но такая замена понятий в чем-то упрощает изложение. Коэффициенты ЭК а, b определяются соотношениями а ≡ 3k(modp); b ≡ 2k(modp); где
k ≡ J(E)(1728 — J(E)) -1 (modp); J(E)≡1728∙4а 3 (4а 3 +27b 2 ) -1 (modp) инвариант ЭК; J(E) ≠ 0∨1728.

Пары чисел (х, у), удовлетворяющие уравнению ЭК, называются ее точками, обозначаемыми Q(х, у), а х и у — координатами точки. В группу точек ЭК в качестве нейтрального элемента включается специальная точка (О) — точка, удаленная в бесконечность (∞), ее координаты обычно не вычисляются. Порядок группы #E(Fq). На множестве всех целых точек ЭК вводится операция сложения. Для двух произвольных точек Q₁(х₁, у₁) и Q₂(х₂, у₂) кривой Е(а,b) суммирование выполняется по различающимся формулам в зависимости от соотношения координат точек.

Построение группы точек ЭК

Пример ЭК. (Формирование группы точек ЭК и построение таблицы Кели). Доопределим ЭК, задав ее коэффициенты (а, b) и поле, над которым будем ее рассматривать. Желательно построить мультипликативную группу поля, так как она потребуется в ходе вычислений, но для индивидуального задания можно ограничиться списком значений обратных элементов мультипликативной группы поля Fр.

получает вид. Эта кривая задана над простым полем Fр с характеристикой р = 23 – простое число. Кривая редуцирована, т.е. приведена по модулю р.

Решение. В заданном поле 23 элемента, но каждая точка кривой имеет две координаты, т.е. кривая задана над плоскостью, образуемой декартовым произведением множества элементов поля

. Группа этой кривой циклическая с генерирующей точкой Р(0, 1). Покажу в деталях, как возникает аддитивная группа ЭК над полем для тех, кто не изучал теорию групп и для тех кто изучал, но возможно плохо ее помнит.

Это возможно первый встречающийся нам случай, когда группа создана не человеком, не природой, например в кристаллах, а математикой, которая есть выдумка людей. Этот случай группы открыт людьми недавно, хотя существовал всегда. Он человеком специально не создавался.

Построим таблицу для левой и отдельно для правой частей ЭК при пробегании переменными х и у по всем элементам поля

. Точками группы ЭК будут те, для которых правая и левая части ЭК совпадают своими значениями (их отыскиваем в таблицах П1, П2). Например, первое совпадение получаем при у = 1 и х = 0, вычеты левой и правой части равны 1=1

Таблица П1–Значения вычетов левых и правых частей ЭК

Таблица П2 – упорядоченные вычеты правой части (по х)

Далее в этой таблице П1 будем находить одинаковые значения вычетов правой и левой частей ЭК по модулю 23 (выделены заливкой). Всем вычетам соответствуют значения х из 2-й строки таблицы П1. Так как в левой части выписан квадрат переменной у, следовательно, при равных значениях вычетов частей одному х будут соответствовать два значения ± у. Но отрицательные значения модулярная арифметика позволяет легко перевести в положительные, т.е. для (– у1) имеем р – у1 = у2.

Значению элемента поля 0 соответствует в правой части 1 и у =± 1, т.е. у1=1,
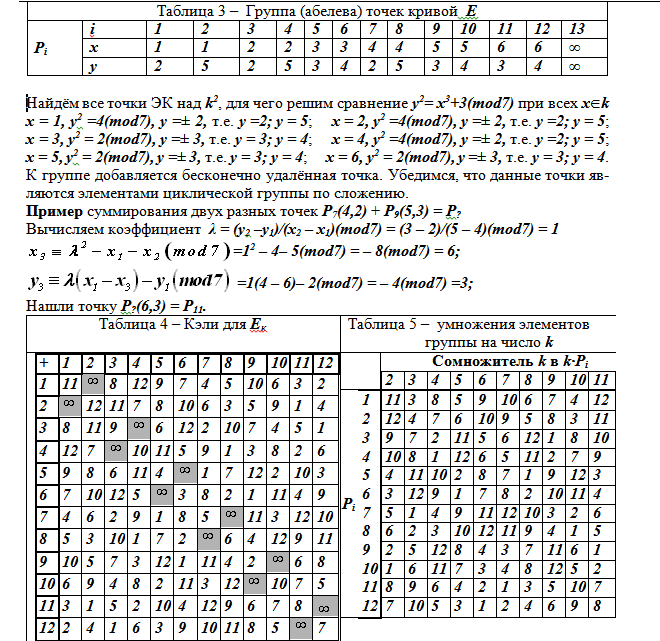
у2 = 23 –1 = 22. Теперь выпишем в таблицу П3 группы точек ЭК координатные пары (х, у) и порядки точек:

(mod p), а = 1, b = 1, дополнительно в группу включается ∞-удаленная точка (28-я по номеру, обозначена ∞).

Это очень важная точка О – нейтральный элемент группы, она не имеет координат. Точке (27-й) с координатой х = 4 пары нет, она сама к себе противоположная. Удвоение этой точки (

) равно ∞-удаленной точке.

В последней строке таблицы 3 вписан порядок (ord) точки.
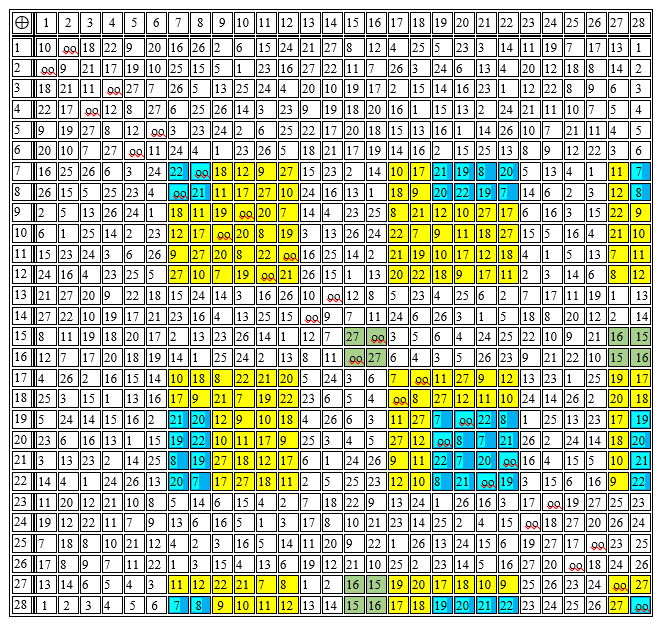
Математик Кэли предложил характеризовать множество результатов таких операций таблицами, которые получили его имя (таблицы Кэли), таблицей сложения для аддитивной группы и таблицей умножения — для мультипликативной. При построении таблицы П4 (таблицы Кели) группы точек и наличии таблицы П3 можно использовать не координаты точек, а их порядковые номера, что более удобно. Номера точек требуют меньше места для записи, чем координаты.

Таблица П4 – Сумма пар точек группы эллиптической кривой

над простым полем GF(23).

В таблице группы ЭК (таблица П4) показаны заливкой разного цвета выявленные подгруппы разного порядка.

Суммирование точек ЭК — групповая операция

Таблица П4 суммы точек группы ЭК получена путем сложения пар (Q1 =(x1, y1); Q2 =(x2, y2)) точек по специальным формулам, а результатом будет третья точка Q3 =(x3, y3).
При равенстве обеих координат у точек х₁= х₂, у₁= у₂≠ 0 имеем удвоение или сумму одной точки с собой. Результирующая точка Q₃(х₃, у₃) получает координаты, вычисляемые по формулам, где λ — коэффициент или тангенс угла наклона прямой (касательной или секущей), соединяющей точки Q1, Q2:
λ ≡ (3х₁ 2 + а)(2у₁) -1 (modp);
х₃ ≡ λ 2 -2х₁(modp);
у₃ ≡ λ(х₁-х₃)-у₁(modp).

При х₁= х₂, у₂= -у₁(modp), точки лежат на вертикальной прямой, пересекающей в них ЭК. Эта прямая пересекает и третью точку (О) ЭК, которая удалена в бесконечности. Сумма двух точек Q₁(х₁, у₁) и Q₂(х₂, у₂) называется нейтральным элементом (нулевой точкой O) группы, координаты которой не определяются.

Суммирование с этой точкой любой другой точки не изменяет эту другую и дает результат Q + О = О + Q = Q +O = Q.
Точка Q имеет кратность k или называется просто кратной точкой Е(а, b), если для некоторой точки Р∊Е(а, b) выполнено равенство Q = Р + Р + …+ Р = kP.

Порядок группы и элемента группы

Определение. Порядок группы — число ее элементов. Каждый отдельный элемент в группе также характеризуется его порядком.

Определение. Порядок (ord, период) элемента в группе — это наименьшее положительное число (кратность k элемента) в операции, при котором результат операции обращается в нейтральный элемент.
а + а +…+ а = ka = 0 в аддитивной или
a∙a∙a∙…∙a = a k = 1 в мультипликативной группе.
Период элемента кратен порядку группы, т.е. делит нацело порядок группы.

Подгруппы точек разных порядков: 27, 28; 2 – порядка (она входит в п/группу 14 порядка),
15, 16, 27, 28; 4 – порядка,
7, 8, 19, 20, 21, 22, 28; 7 – порядка,
7,8,9,10, 11,12, 17,18,19,20,21, 22,27, 28; 14-го порядка,

Пример П1. Все 28 элементов образуют циклическую группу ЭК, но генератором может быть только элемент 28 порядка, например, Р (0, 1). Многократно суммируя этот элемент с собой сумма проходит через все элементы группы.

Порядок каждого из элементов (точек) группы находится многократным суммированием по таблице П4 пока сумма не станет нейтральным элементом. Например,

Кратные элементов образуют подгруппы (циклические):

образуют циклическую подгруппу 4-го порядка.
Это нормальная подгруппа и по ней можно разложить исходную группу в смежные классы. В свою очередь эти смежные классы рассматриваются как элементы факторгруппы, т.е. они образуют группу 7-го порядка по числу смежных классов.

Операция суммирования всех целых точек Е(а,b) вместе с нулевой точкой О (нейтральный элемент) порождает конечную (коммутативную) аддитивную (абелеву) группу порядка q, где q ≠ p. Для этого порядка справедливо установленное Хассе соотношение р + 1 — 2√р

циклическая группа порядка n. Одно из свойств – односторонность зависимостей кратных базовой точке других точек группы – нашло применение с учетом использования модулярной арифметики в двухключевой криптографии, а в ней для шифрования и цифровой подписи.
Пример П2. Вычисление порядка группы ЭК

над простым полем GF(23). Пусть генератор группы с порядком 28 Q =(0, 1).Тогда имеем полный список кратных генератору точек:

1Q =(0, 1); 2Q =( 6,-4); 3Q = (3,-10); 4Q =(-10,-7); 5Q =(-5, 3); 6Q =(7,11); 7Q =(11,3);
8Q =(5,-4); 9Q =(-4,-5); 10Q=(12,14); 11Q =( 1, -7); 12Q=(-6,-3); 13Q=(9,-7); 14Q =( 4,10);
15Q=(9,7); 16Q=(-6, 3); 17Q= ( 1, 7); 18Q =(12,-4); 19Q=(-4, 5); 20Q=(5, 4); 21Q=(11,-3);
22Q=(7,-11); 23Q=(-5,-3); 24Q= (10,7); 25Q = (3,10); 26Q=( 6, 4); 27Q=(0,-1); 28Q=(∞);

Пример S. Суммирование кратных точек группы ЭК. При наличии полного списка кратных точек группы упрощается вычисление комбинаций таких кратных точек. Пусть требуется вычислить сумму 3Q =(3,-10) и 7Q =(11,3).
Решение. Очевидно должно быть 3Q +7Q =10Q. Убедимся в этом, будем считать, что суммируются две какие-то точки из группы: Q1 =3Q и Q2 =7Q их координаты заданы.

Обрабатывается результирующая точка Q₃(х₃, у₃), она получает координаты, вычисляемые по формулам:
λ ≡(у2-у1)/(x2-x1)(mod23)=(3-(-10)/(11-3)(mod23)=13/8(mod23); Так как 8 -1 ≡3(mod23), то λ≡13/8 ≡13•3(mod23)=16;
х₃ ≡ λ 2 -2х₁(modp)=λλ -x1 -x2≡(16•16-3-11)(mod23)=12;
у₃ ≡ λ(х₁-х₃)-у₁(modp)≡λ(x1-x3)-y1(mod23)≡(16-12-(-10))(mod23)=14.
Ответ х3=12; у3 =14 или Q3 = (12, 14)=10Q.

Отсюда следует, что для понимания проблемы применимости ЭК в криптографии первой решаемой задачей должна быть задача установления и последующий анализ группы G точек конкретной ЭК. С этого важного положения мы и начнем рассмотрение и установление группы G точек ЭК над фиксированным конечным простым полем F(р), элементы которого оказываются координатами обнаруживаемых точек кривой. Здесь же определим порядок каждой найденной точки, порядок самой группы G, перечислим подгруппы, входящие в состав основной группы G.

Покажем, как основная группа G раскладывается в смежные классы по каждой подгруппе, как после этого возникают факторгруппы. Построим таблицы Кели для группы G и для факторгруппы. В криптологических публикациях принято, если приводится числовой пример, то желательно уже известный, знакомый по другим публикациям.Это обеспечивает сопоставимость результатов и более быстрое вникание в существо вопроса. Придерживаюсь этого правила и я.

Проблема факторизации составных натуральных чисел многие столетия удерживает внимание специалистов в различных теоретических (научных) и прикладных областях таких как числовые системы, вычислительная математика и техника, теория чисел, информационная безопасность, криптография, и др., и вынуждает их прикладывать немалые усилия к ее положительному и успешному решению.

Тем не менее, проблема и сегодня далека от ее закрытия, завершения. Автор предлагает к рассмотрению и стремится дать читателю понятие о существующих подходах к решению проблемы, ставших уже своеобразной классикой, привести критику и выразить одобрение замечательным находкам.

В работе излагается один из известных подходов к решению задачи факторизации больших чисел (ЗФБЧ), использующий математику эллиптических кривых (ЭК). Об этой математике, а точнее о технике вычислений приведу цитату авторов из [ 1 ]

«Техника, используемая в настоящее время при изучении ЭК, является одной из самых изощренных во всей математике. Мы надеемся, что элементарный подход настоящей работы побудит читателя к дальнейшему изучению этой живой и пленительной ветви теории чисел. Есть много того, что следует изучить, и много работы, которую еще надо проделать»

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Метод факторизации числа, использующий эллиптическую кривую

Алгоритм факторизации числа

В этом вероятностном алгоритме отображены основные черты его изложения в работах [3, 7, 9].
1. Выбираются числа M и N и числа 1 2 — х 3 — ах(modN). После чего для ЭК у 2 ≡ х 3 + ах + b(moN), где а, b, х, у ∊ Fр выбираем точку Р = (х, у);
3. Находим d = НОД(N, 4а 3 + 27b 2 ), если 1 d2 3 d3 5 d5 …r dr . Здесь 2, 3, 5, …, r несколько первых простых чисел, а d2, d3, d5,…dr -малые положительные числа. После этого вычисляется а k -1 по модулю N и затем (N, а k -1), что требует для вычисления 2ℓog₂ (2kN) операций. При этом даже если k и N имеют в записи по тысяче знаков время расчетов оказывается вполне приемлемым.

Если (N, а k -1) ≠ N, то получаем нетривиальный делитель числа N. При этом N раскладывается на два множителя и, если они составные, то к каждому из них применяется эта же процедура. При (N, а k -1) = N, переходим к новому выбору параметра а. Если же (N, а k -1) = 1, то переход к новому значению k большему предыдущего. В работе [3] приводится средняя оценка сложности:
е ((2 + о(1))ℓogpℓogℓogp) 1/2 ℓog 2 N для этого алгоритма, здесь р — минимальный простой делитель N.
Конкретный числовой пример факторизации числа приводится ниже с пояснениями отдельных вычислительных элементов.

Пример Ф. Этот пример показывает возможность решения задачи факторизации числа (составного модуля числового кольца вычетов) с использованием ЭК. В основу алгоритма положено многократное суммирование точки ЭК с собой, т.е. вычисление аддитивного порядка точки ЭК. Этот порядок делит порядок группы точек ЭК.

При этом возможно, что решение задачи факторизации появляется раньше, чем будет найден порядок точки в процессе вычисления кратных точек. Нахождение суммы двух точек требует вычисления коэффициента λ, для чего привлекается расширенный алгоритм НОД(N, х₂-х₁) Евклида.

Если значение d = НОД >1, и d ≠ N, то делитель N найден и факторизация выполнена. В примере все вычисления проводятся в конечном числовом кольце вычетов с модулем
N = 455839 = 599∙761. Выбрана ЭК Е: у 2 ≡ х 3 + 5х-5(modN), где
а = b = 5 ∊ ZN и дискриминант Е(а, b) равный -4а 3 + 27b 2 ≢ 0(modN) не сравним с нулем по модулю N. Задана также рациональная точка Р=(1,1) на ЭК. Будем многократно суммировать эту точку с собой. Рано или поздно такое суммирование приведет к результату-нейтральному элементу-точке (0), так как каждый элемент алгебраической структуры имеет период.

Конечно, это суммирование очень длительный процесс, но алгоритм, оказывается, может приводить к решению часто и на промежуточном шаге вычислений. Поэтому при больших числах сначала будем находить небольшую сумму точек, например,
10! Р = 2 8 ∙3 4 ∙5 2 ∙7Р = 3628800∙Р и при их недостатке увеличивать число.

Начнем с удвоенной точки Р₂ = P + P=2! Р =1∙2∙Р.
Обрабатывается точка Р₂ = 2Р. Находим для Р₂ значение коэффициента λ и затем координаты точки Р₂
λ≡(3х₁ 2 + а)(2у₁) -1 (modN) = (3∙1 2 + 5)/(2∙1)≡4(modN);
х₂ ≡ λ 2 -2х₁(modN)= 4 2 -2∙1(modN) =14;
у₂ ≡ λ(х₁-х₂)-у₁(modN)=4(1-14)-1(modN)=-53(modN)=>-53(modN)=455839-53=455786.

При фиксированном х₂, х₂ ≠ 0, на ЭК имеется две точки с разными координатами у₂, дополняющими друг друга до модуля. Легко убедиться подстановкой координат в уравнение ЭК, что полученная точка Р₂ = ( х₂, у₂) = (14, -53) лежит на ЭК.
у₂ 2 = (-53) 2 = 2809 = 14 3 + 5∙14-5 = 2744+70-5 = 2809(modN), Р₂ ∊ Е. Левая часть уравнения равна правой.

Вычисление λ в формуле содержит деление на 2у, но в операции деления в алгебраических структурах нет. Деление заменяется умножением на обратный элемент, получаемый через НОД.
Далее вычисляем точку 2Р₂ = 4Р и к ней приплюсуем точку Р₂ = 2Р.

Обрабатывается точка 2Р₂ = 4Р. Находим для 2Р₂ значение коэффициента λ и координаты 2Р₂
λ ≡ (3х₂ 2 +а)(2у₂) -1 (modN) =(3∙196 + 5)/(2(-53))=-593/106 = 322522(mod455839);
х₂ ≡ λ 2 -2х₁(modN) =322522 2 -2∙14(modN)=104020440484-28(455839) =259851;
у₂≡λ(х₁-х₂)-у₁(modN)=116255(mod455839).

Проверка принадлежности точки Р= (259851, 116255) эллиптической кривой:
Е: у 2 ≡ х 3 + 5х-5(modN); 116255 2 (mod455839)=54514;
259851 3 + 5∙259851 -5 =17545800113472051+1299255-5(mod455839) = 54514.

При вычислениях коэффициента λ = 322522 используется арифметика поля, кольца и ЭК. Дело в том, что в алгебраических структурах отсутствует операция деления на число. Когда она появляется в формулах, ее необходимо исключить, что делается путем умножения на элемент обратный, стоящему в знаменателе формулы.

Получение мультипликативного обратного элемента в кольце вычетов

Пример ОБ.Определение обратного элемента возможно, если элемент обратим (в конечном кольце вычетов не все элементы имеют обратные). Для выражения λ=-593/106(mod455839) имеем как раз такой случай, т.е. для элемента 106 необходимо определить обратный к нему элемент в конечном кольце по модулю N.

Покажем как это делается в нашем примере; привлекается расширенный алгоритм Евклида поиска наибольшего общего делителя двух чисел: модуля 455839 и знаменателя λ числа 106:
455839 = 4300∙106 + 39;
106 = 2∙39 + 28;
39 = 1∙28 + 11;
28 = 2∙11 + 6;
11 = 1∙6 + 5;
6 = 1∙5 + 1.

Получили, что НОД(455839, 106) = 1. После этого обратным ходом находим обратный элемент для числа 106;
1= 6-5 = 2∙6-11 = 2∙28-5∙11 = 7∙28-5∙39 = 81707∙106-19∙455839 => 81707∙106-19∙455839 ≡ 1(mod455839) =>81707∙106 ≡ 1(mod455839) и, окончательно, 1/106 ≡ 81707(mod455839).

Тогда λ =-593/106(mod455839) => λ =-593∙81707(mod455839) = 322522.
Для получения точки Р₃ надо суммировать две разные ранее найденные точки 2Р и 4Р. Вычисляется коэффициент λ (по другим формулам) для этого случая и координаты точки.

Далее вычисляем точку Р₃ = 3! Р = 1∙2∙3∙Р = 6Р = 2Р + 4Р. Нашли уже ранее значение 2Р₂ = 4Р, которое получали суммированием точки 2Р с собой. Для 2P + 2P = 2Р₂ определяем значение коэффициента. Используем те же формулы.

Обрабатывается точка 3Р₂ =3! Р= 6Р. Находим для 3Р₂ значение коэффициента λ и ее координаты
λ ≡ (у₂-у₁)(х₂-х₁) -1 (mod455839);
х₃ ≡ λ 2 -х₁-х₂(modN) = 195045(mod455839);
у₃ ≡ λ(х₁-х₃)-у₂(modN) = 123227(mod455839).

Продолжая вычисления тем же порядком для точек Р₄ = 4! Р, Р₅ = 5! Р… Р₈ = 8! Р, для которой знаменатель в формуле для λ получает значение равное 599, в процессе вычисления
d= НОД(455839, 599) получаем d = 599, т.е. это делитель N, что и завершает задачу факторизации. Другой делитель получаем делением на первый N/599 = 761. Оба делителя простые числа.

Еще одно применение ЭК в криптологии — это построение криптографической системы (КГС).

Простая криптографическая система на эллиптических кривых

В сети обмена данными для всех абонентов задается общая редуцированная эллиптическая кривая Е_a,b(F_р) над полем F_р и порождающая точка
Р = (х, у) на ней.

Каждый абонент, используя точки аддитивной группы этой ЭК формирует свои открытый и закрытый ключи. Ниже в примере 2 рассматривается простой вариант криптографической системы (КГС) с возможностью шифрования/расшифрования сообщений элементами группы точек ЭК. Понимание основ теории эллиптических кривых и смежных вопросов открывает возможности использование богатого арсенала их средств в целях повышения уровня безопасности информационных систем и предотвращения возможных нападений на них.

Основные правила протокола. Отправитель шифрует свое сообщение открытым ключом получателя, получатель использует личный ключ для расшифрования получаемых шифрованных сообщений. Открытые ключи всех абонентов доступны всем, закрытые (личные) ключи хранятся в тайне от всех.

Шифрование: Пусть отправитель В посылает получателю А сообщение в виде исходного текста (ИТ) одного трехбуквенного слова «ДОМ»
Эти символы необходимо преобразовать в цифровую (двоичную) форму, например, ASCII кодом.
ИТ =

Для посимвольного шифрования сообщения абоненту В требуется открытый ключ абонента А. Этот ключ абонент А формирует и публикует как общедоступный в сети связи.
Открытый ключ А: точка генератор группы ЭК Q=P5=(3,3). Выбор этой точки достаточно произволен.

Далее А вырабатывает случайное число а = 3 которое для абонента А является личным (иногда называют секретным ключом) ключом. Точка Q умножается на личный ключ. Получается точка N =аQ =3Q =3P5 = P11 =(6,3). окончательно открытый ключ имеет вид: Q,N.

Отправитель В вырабатывает свое случайное число b=2 и умножает обе точки ЭК открытого ключа Q и N на b=2: получает точки R=bQ =P4 = (2,5); S =bN = baQ = P8 = (4, 5).

Далее координаты точки S = (4, 5) преобразуются к двоичному представлению S = P8 = (4, 5) = (0000 0100, 0000 0101). Символы сообщения и координата хs преобразуются после этого в шифрованный текст (ШТ). Простейший вариант преобразования текста сообщения операцией ЕХОR
ШТ =.

Отправитель В посылает получателю А точку ЭК R и шифрованное сообщение ШТ.
Расшифрование: выполняет сторона А — получатель сообщения. Точка R кривой умножается на личный (секретный) ключ (а) абонента А: аR =аbQ = S = 3P4 = P8 = (4,5), что также дает точку S = P8 = (4,5). После этого абонент А выполняет расшифрование, получая исходный текст ИТ.

Здесь изложен весьма упрощенный вариант обмена шифрованными сообщениями, когда оба абонента используют один общий ключ. В действительности каждый символ исходного текста может представляться точкой ЭК или координатой такой точки. В последнем случае для преобразования используется групповая операция суммирования точек ЭК по модулю.

k — число слагаемых равных точке Рi соответствующей строки. В ячейках таблиц 4 и 5 помещены номера i точек Pi из таблицы 3, где представлены все 13 точек конечной аддитивной группы эллиптической кривой у 2 ≡ х 3 + 3(mod7)

Заключение

Детально рассмотрены вопросы построения ЭК, группы ее точек, подгруппы, порядки подгрупп и элементов. Приводятся поясняющие числовые примеры.
Арифметика ЭК (сложение точек, вычисление кратных точек, обратного элемента в группе ) все иллюстрируется числовыми примерами.
Формулируется задача факторизации составного числа в терминах теории ЭК.
Приводится пошаговый алгоритм вычисления сомножителей фактризуемого составного числа.
Пример использования ЭК для построения криптографической системы защиты сообщений.