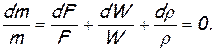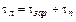Дозвуковое и сверхзвуковое течения газов (основы газодинамики)
1. Адиабатически установившееся течение газа.
2. Уравнение Гюгонио. Сопло Лаваля.
3. Уравнение состояния.
4. Удельные теплоемкости газа.
5. Первый закон термодинамики. Энтальпия. Энтропия.
6. Характеристики заторможенного потока. Газодинамические
Видео:Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

Рекомендуемые файлы
7. Волна разрежения.
8. Скачок уплотнения.
9. Гиперзвуковые течения. Формула Ньютона.
При скоростях движения жидкости сравнимых со скоростью звука или их превышающих, на первый план выдвигаются эффекты, связанные с сжимаемостью жидкости. Такое движение на практике наблюдается в газах. Поэтому о гидродинамике больших скоростей говорят обычно как о газодинамике.
Чаще всего в газодинамике приходится иметь дело с очень высокими значениями чисел Рейнольдса. За исключением отдельных случаев ( наиболее ярким из которых является отрыв сверхзвукового потока ) при высоких значениях числа Рейнольдса вязкость оказывается не существенной для движения газа практически во всем пространстве. Поэтому в газодинамике часто газ рассматривают как идеальную жидкость.
Движение газа имеет существенно различный характер в зависимости от того, является оно дозвуковым или сверхзвуковым.
С изучением сверхзвуковых течений связано решение ряда практических проблем, возникающих при создании самолетов, ракет, турбин, снарядов, аэродинамических труб для получения потоков со сверхзвуковыми скоростями.
12.1. Адиабатическое установившееся течение газа
Изучение движения газов с высокими скоростями, достигающими скорости звука, является предметом газовой динамики. Одной из фундаментальных задач последней является исследование течений без учёта сопротивлений и в отсутствие теплообмена (т.е.) адиабатических. В этих условиях уравнение баланса удельной энергии имеет вид

Уравнение адиабаты идеального газа представим в виде

Будем отмечать в дальнейшем индексом «0» величины, характеризующие газ, находящийся в покое, или, как говорят в газодинамике, в заторможенном состоянии, подставим в уравнение неразрывности
и после интегрирования

При установившемся течении весовой расход газа во всех сечениях по длине газопровода одинаков в течение всего процесса движения.
Следовательно, при установившемся течении

что является выражением условия неразрывности при движении газа (и также сжимаемых жидкостей). В трубопроводе постоянного сечения одинаковой по длине трубопровода будет также весовая скорость

Изменение в удельном весе (плотности) идеального газа при изменении давления и температуры выражаются законом Клайперона-Менделеева

где Т — абсолютная температура газа, R — газовая постоянная.
В технике имеют особое значение изотермическое и адиабатическое течения газа. При изотермическом (Т=const) течении идеального газа зависимость между давлением и плотностью имеет вид


где 
Имея в виду последнее соотношение, можно записать


Имея в виду, что v = 0 при p=p0 (состояние покоя), найдём:



12.2. Уравнение Гюгонио. Сопло Лаваля
Запишем уравнение Бернулли в дифференциальной форме

Преобразуем уравнение Бернулли для газа так, чтобы можно было ввести число Маха. Имеем

квадрат скорости звука 

Поделим на a 2 , получим

или в окончательном виде

где M — число Маха.
Другим уравнением, необходимым для анализа течений газа в трубе переменного сечения, является уравнение неразрывности, или сохранения массы.
Будем рассматривать одномерное установившееся течение газа вдоль трубы переменного сечения, при этом предположим, что параметры потока газа, такие, как скорость потока, давление и плотность, одинаковы во всех точках каждого из конечных сечений, перпендикулярных к оси трубы.
Это предположение довольно хорошо соответствует действительности для элементарной трубки тока, но его применяют и для труб конечных размеров, используя средние величины по сечениям трубы.
Через каждое поперечное сечение трубы в случае одномерного течения проходит за 1 с масса газа m=Svr, где S — площадь поперечного сечения трубы, v — скорость течения газа, r — плотность газа. При установившемся течении через все поперечные сечения должна пройти одна и та же масса газа, т.е.

Прологарифмируем это уравнение сохранения массы. Получим

Считая переменными величины S, v, r, возьмём полные дифференциалы от обеих частей. Имеем

Это и есть уравнение неразрывности для установившегося одномерного течения идеального газа в трубе переменного сечения.

Из уравнения неразрывности и уравнения Бернулли исключим величину

Это уравнение носит название уравнения Гюгонио.
Используя уравнение Гюгонио, проанализируем характер возможных течений газа в трубе переменного сечения.
Из уравнений следует:
1) при M 1, знаки dS и dv одинаковы, т.е. сверхзвуковой поток расширяется противоположно дозвуковому. Чтобы увеличить его скорость, трубу следуeт расширить,
3) при M = 1 имеем dS = 0, т.е. в этом случае S достигает максимума или минимума. Можно показать, что M = 1 может быть только в самом узком сечении трубы, где S=Smin.
Выводы о характере течений газа в трубах переменного сечения нашли применение в конструкциях сопел современных ракетных двигателей и аэродинамических трубах больших скоростей. Для получения больших сверхзвуковых скоростей выходящего из сопла газа следует сначала сопло сужать, чтобы получить звуковую скорость газа в узком сечении сопла, а затем сопло надо расширять для дальнейшего увеличения скорости выходящего из него газа.

Наибольшая скорость, которая может быть получена на выходе из сопла, зависит от площади выходного сечения и должна обеспечиваться необходимым для данной скорости давлением на входе в сопло ( рис. 58 ).
Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Геометрическое воздействие. Уравнение Гюгонио
На практике мы наиболее часто сталкиваемся с геометрическим воздействием на течение жидкости, когда имеет место только изменение площади проходного сечения канала по длине. Это прежде всего сопла и диффузоры реактивных двигателей, компрессоров и турбин. Изучение этих течений как одномерных при условии отсутствия других воздействий является наиболее простым для анализа.
Продифференцировав уравнение неразрывности (расхода) для изолированного одномерного течения (для элементарной струйки)
где m – массовый расход, ρ – плотность, W – скорость жидкости, а F – площадь проходного сечения канала;
и разделив почленно на m=ρWF, получим дифференциальное уравнение неразрывности
Исключим из этого уравнения член, учитывающий изменение плотности. С этой целью преобразуем уравнение Бернулли для изолированного течения (для элементарной струйки):

с учетом выражения для скорости звука

Подставив последнее выражение для плотности в дифференциальное уравнение неразрывности, получим частный случай уравнения обращения воздействия для случая геометрического воздействия на течение жидкости – уравнение Гюгонио:
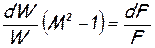
которое показывает, что
дозвуковой поток (при M 0 ) в сужающихся каналах ( dF 0),
а сверхзвуковой поток (при M>1) наоборот
— ускоряется (dW>0 ) в расширяющихся каналах ( dF>0)
и тормозится (dW
Видео:Горицкий А. Ю. - Уравнения математической физики - Условие Ранкина-ГюгониоСкачать

Для ударных волн. Адиабата Гюгонио
Преобразуем полученные уравнения. Уравнение (1) можно представить в виде
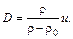
Так как при сжатии газа 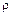
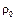
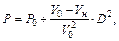
проходящую через начальную точку 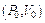
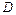
Уравнение Гюгонио принимает следующий вид:
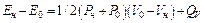
где 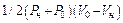
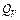
Рисунок 14 – Кривая Гюгонио для детонационной волны
Кривая Гюгонио для детонационной волны (АС) построена для конечных продуктов реакции, обладающих повышенным содержанием энергии и поэтому лежит выше кривой Гюгонио для ударной волны.
Для процессов детонации реальное значение имеет лишь ветвь (CH) на кривой Гюгонио, так как вдоль этой ветви, как следует из уравнения (1) и (2) 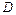
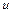
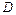
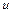
Проведем из точки A 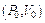
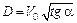
Чепмен и Жуге обосновали следующее:
«Процессу детонации отвечает лишь одно единственное состояние продуктов взрыва, характеризуемое точной энтальпией, в которой прямая Михельсона касается адиабаты Гюгонио для продуктов детонации. В этой точке 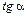
2.4 Механизм распространения детонации по
конденсированным взрывчатым веществам
Гидродинамическая теория детонации для газов применима и к конденсированным ВВ. Фронт детонационной волны также представляет собой ударную волну, в которой ВВ сжимается. При сжатии поглощается энергия, которая компенсируется энергией, выделяющейся в результате химической реакции. Таким образом, интенсивность ударной волны поддерживается, и её должно быть достаточно, чтобы вызвать детонацию в соседнем слое. Однако, ввиду малой сжимаемости конденсированных ВВ разогрев достаточный для достижения скорости реакции, может возникнуть только при скорости детонации порядка
В случае ВВ, детонирующих с меньшей скоростью, разогрев за счет гомогенного сжатия становится недостаточным для того, чтобы реакция разложения имела большую скорость.
По А.Я. Апину детонация порошкообразных ВВ представляет собой своеобразное «взрывное горение» отдельных частиц ВВ. Эти частицы воспламеняются в результате адиабатного сжатия газовых включений или струями горячих продуктов взрыва. Нагрев и воспламенение могут осуществляться также при трении частиц друг о друга при сжатии их во фронте детонационной волны.
2.5 Опытное определение скорости детонации
2.5.1 Метод Дотриша
Скорость детонации определяют с помощью специальных приборов – хронографов, причем существует несколько различных методов. Наиболее точным из них является метод детонирующего шнура (метод Дотриша).
Сущность метода в том, что неизвестная скорость детонации заряда сравнивается с известной скоростью детонации детонирующего шнура.
 |
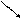 |
 |
 |
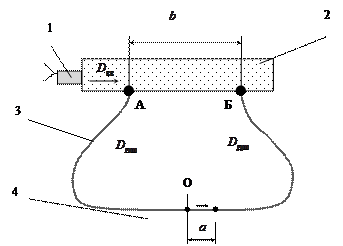
1 – электродетонатор (или капсюль-детонатор); 2 – заряд ВВ;
3 – отрезок детонирующего шнура; 4 – свинцовая пластина
О – середина отрезка шнура; В – метка на пластинке после взрыва
Рисунок 15 – Схема определения скорости детонации по Дотришу
Расстояние между концами шнура является базой для определения скорости детонации и должно быть точно измерено. В левом конце шнура детонация начинается раньше, чем в правом, поэтому место столкновения волн сдвинется вправо и будет находится в точке В, где находится метка от взрыва. В точке О середина шнура. Расстояние между точками О и В обозначим через 
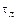
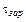
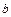
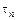
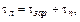
где 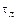
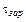
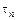
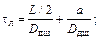
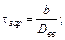
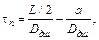

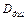
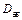

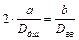
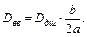
Для этого метода достаточно знать 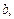
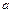
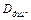
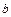
2.5.2 Фотографический метод
Для фотографирования применяются приборы, называемые фоторегистрами. Существует два типа фоторегистров:
🎬 Видео
Адиабатный процесс. 10 класс.Скачать

§21 Каноническое уравнение гиперболыСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Уравнения Гамильтона (динамика)Скачать

Уравнивание реакций горения углеводородовСкачать

Шрёдингер и его уравнение — Дэвид Клэри / ПостНаукаСкачать

Урок 455. Уравнение ШрёдингераСкачать

Гальванические элементы. 1 часть. 10 класс.Скачать

Закон БернуллиСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать