Видео:§29 Эксцентриситет гиперболыСкачать
Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:
,
где a и b — длины полуосей, действительной и мнимой.
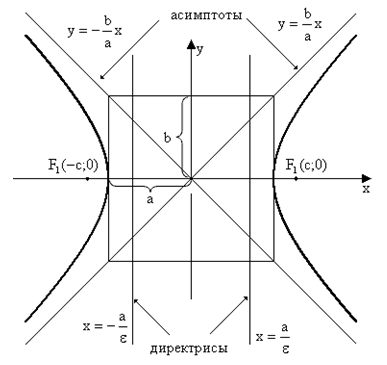
На чертеже ниже фокусы обозначены как 
и 
.
На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:
.
Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 
и 
, где
,
называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:
.
Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
.
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:
.
Результат — каноническое уравнение гиперболы:
Если 
— произвольная точка левой ветви гиперболы (
) и 
— расстояния до этой точки от фокусов 
, то формулы для расстояний — следующие:
.
Если 
— произвольная точка правой ветви гиперболы (
) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы
,
где 
— расстояние от левого фокуса до точки любой ветви гиперболы, 
— расстояние от правого фокуса до точки любой ветви гиперболы и 
и 
— расстояния этой точки до директрис 
и 
.
Пример 4. Дана гипербола 
. Составить уравнение её директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 
. Вычисляем:
.
Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями
.
На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:
, где 
.
В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 
и координаты точки 
, лежащей на гиперболе. Составить уравнение гиперболы.
Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 
. Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.
.
Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Видео:Видеоурок "Гипербола"Скачать
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы 
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать
Калькулятор онлайн.
Построение графика
дробно-линейной функции (гиперболы).
Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.
Эта математическая программа для построения графика дробно-линейной функции (гиперболы) сначала делает преобразование вида
$$ y= frac ; rightarrow ; y= frac +q $$
а затем последовательно строит графики функций:
$$ y= frac $$
$$ y= frac $$
$$ y= frac +q $$
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода дробно-линейной функции, рекомендуем с ними ознакомиться.
В качестве переменной можно использовать только x
Все остальные буквы недопустимы.
При вводе можно использовать только целые числа.
Видео:Задание №868 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать
Каноническое уравнение гиперболы по двум точкам
| Две точки с координатами |
| Первая координата |
| Вторая координата |
| Каноническое уравнение гиперболы | ||||||||||||
| Большая полуось гиперболы | ||||||||||||
| Малая/мнимая полуось гиперболы | ||||||||||||
| Эксцентриситет гиперболы | ||||||||||||
| Фокальный параметр | ||||||||||||
| Фокальное расстояние | ||||||||||||
| Перицентрическое расстояние | ||||||||||||
Уравнение гиперболы в каноническом виде имеет вот такой вид. Так же как и при расчете уравнения эллипса по двум точкам, мы можем по двум точкам однозначно построить гиперболу, выраженную через вышеуказанную формулу. Используя универсальный калькулятор расчет кривой второго порядка на плоскости по точкам, мы легко определим значения и
Кроме этого, зная эти параметры можно рассчитать следующее: Большая полуось — расстояние от центра гиперболы, до одной из вершин Фокальное расстояние — расстояние от центра гиперболы до одного из фокусов Мнимая полуось — расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат Связь между тремя параметрами выражена в одной формуле Эксцентриситет — коэффициент, численно равный, отношению фокусного расстояния к большой полуоси гиперболы Перицентрическое расстояние — расстояние от фокуса до ближайшей вершины гиперболы Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать  Примеры задачCоставить каноническое уравнение гиперболы по двум точкам Вводим данные в поля ввода. Можем писать как выражение, учитвая что квадратный корень обозначается sqrt, а можем сначала получить численные значения и подставить уже окончательные результаты. В результате получим
|
