Уравнение гиперболы и параболы изображенных на рисунках

Алгебра | 5 — 9 классы

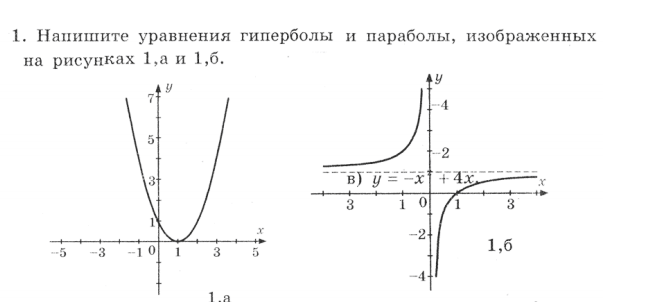
Напишите уравнение гиперболы и параболы!

(на рисунке все есть).

Видео:Как легко составить уравнение параболы из графикаСкачать

Что такое парабола и что такое гипербола?

Что такое парабола и что такое гипербола?

Покажите на схеме и напишите четко для чего они нужны и как ими пользуются.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Как найти точки пересечения параболы и гиперболы?

Как найти точки пересечения параболы и гиперболы?

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Напишите уравнение касательной к параболе : н в точке с ординатой 6?

Напишите уравнение касательной к параболе : н в точке с ординатой 6.

Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Парабола, изображенная на рисунке?

Парабола, изображенная на рисунке.

Видео:Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Напишите уравнение оси симметрии параболы у = х ^ 2 + 6х — 3?

Напишите уравнение оси симметрии параболы у = х ^ 2 + 6х — 3.

Видео:Задание 10 Квадратичная функция Знаки коэффициентов а и сСкачать

Напишите уравнение параболы если известно что парабола проходит через точку ( — 1, 6) , а её вершиной яв — ся точка (1, 2)?

Напишите уравнение параболы если известно что парабола проходит через точку ( — 1, 6) , а её вершиной яв — ся точка (1, 2).

Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Напишите уравнения параболы y = kx в кубе пересикающий через точку К( — 2 : — 20)?

Напишите уравнения параболы y = kx в кубе пересикающий через точку К( — 2 : — 20).

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

График функции : либо через параболу решается либо через гиперболу?

График функции : либо через параболу решается либо через гиперболу.

X во второй + 4х + 3 = 0.

Видео:✓ Четыре способа решить новую задачу из ЕГЭ | Задание 10. Демоверсия ЕГЭ-2023 | Борис ТрушинСкачать

Графиком уравнения x2 + y2 + 26x = 0 является : 1?

Графиком уравнения x2 + y2 + 26x = 0 является : 1.

Гипербола, которая пересекает ось х 2.

Парабола с вершиной 3.

Парабола, которая пересекает ось у 4.

Окружность с центром В точке с координатами ( — — ; — — ).

Видео:Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Какая это элементарная функция(парабола, гипербола, прямая и тд)?

Какая это элементарная функция(парабола, гипербола, прямая и тд)?

Если вам необходимо получить ответ на вопрос Напишите уравнение гиперболы и параболы?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Алгебра вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Дана функцияy = — 2x² — x + 3. График её — парабола ветвями вниз. Находим координаты её вершины. Хо = — в / 2а = 1 / (2 * ( — 2)) = — 1 / 4. Уо = — 2 * (1 / 16) + (1 / 4) + 3 = 50 / 16 = 3, 125. Находим точки пересеченияграфикомоси Ох (при этом ..

1) x + 2≥ 0 2) x² — 2≠ 0 x≥ — 2 x² ≠ 2 x≠√2 и x≠ — √2 _______₀___________________₀___________ — 2 — √2 √2 |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| x∈ [ — 2 ; — √2)∪ ( — √2 ; √2)∪ (√2 , + ∞).

Если sinx + sin2x = 1 sinx + 2 sinx cosx = 1 sinx×(1 + 2cosx) = 1 sinx = 1 или 1 + 2соsx = 1 x = π÷2 + 2πk 2cosx = 0 2x = π÷2 + πk x = π÷4 + πk÷2.

2сos²x + 3sin2x — 8sin²x = 0 8sin²x — 3sin2x — 2cos²x = 0 8sin²x — 6sinxcosx — 2cos²x = 0 | : 2cos²x, cosx≠ 0 4tg²x — 3tgx — 1 = 0 Пусть t = tgx. 4t² — 3t — 1 = 0 D = 9 + 4·4 = 25 = 5² t₁ = (3 + 5) / 8 = 8 / 8 = 1 t₂ = (3 — 5) / 8 = — 2 / 8 = — 1 / ..

Газы : расстояние между молекулами превышает размеры самих молекул, взаимодействие молекул слабое, движение хаотическое. Газы облатают летучестью, не сохраняют форму и объём. Жидкости : молекулы расположены вплотную друг к другу, могут совершать ко..

Это решала под д не знаю не получается ну первое правельно там нет решешения.

Это двадцать знаков.

(y — 4)(y + 2) — (y — 2) ^ 2 = y ^ 2 + 2y — 4y — 8 — y ^ 2 + 4y — 4 = 2y — 12.

Скачай photomath можно простотчерез камеру навести на вопрос и вжух ответ.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Видео:Новая задача №9 на гиперболу из ЕГЭ 2022 по математикеСкачать

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Видео:ПАРАБОЛЫ И ГИПЕРБОЛЫ НА ИЗИСкачать

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Видео:ОГЭ. Задание 11. Графики.Скачать

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:ОГЭ Задание 10 Найти коэффициент a по графику квдратичной функцииСкачать

Уравнение гиперболы и параболы изображенных на рисунках

Вопрос по математике:

Напишите уравнения гиперболы и параболы изображённых на рисунках

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

📹 Видео

Как определить уравнение параболы по графику?Скачать

10 задание. Все графики ЕГЭ по математике 2023Скачать

Задание 5 ОГЭ по математикеСкачать

ОГЭ по математике. Задание 5. Уравнение параболы. Коэффициент c.Скачать

ОГЭ. Задание 11. ГрафикиСкачать