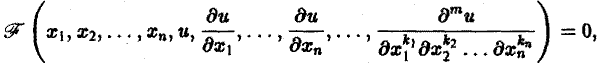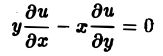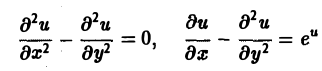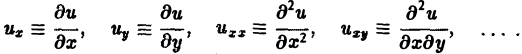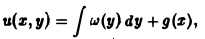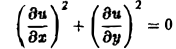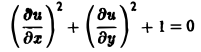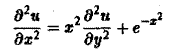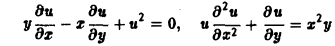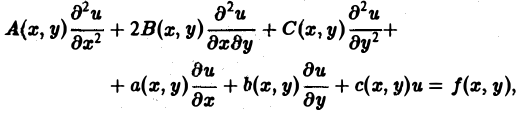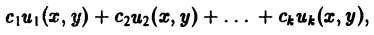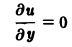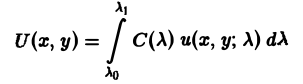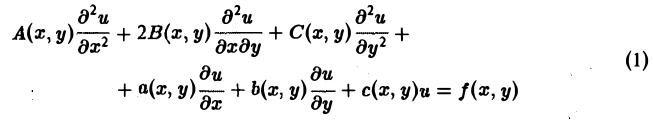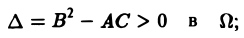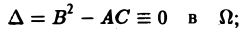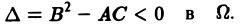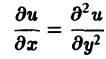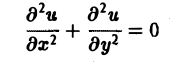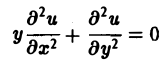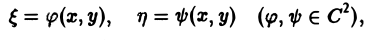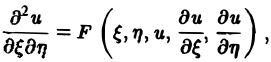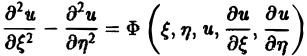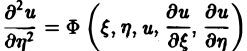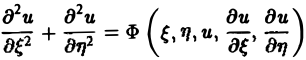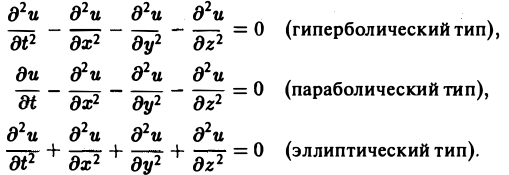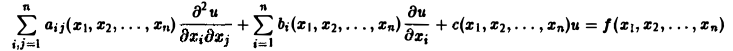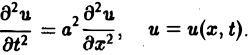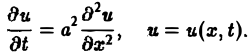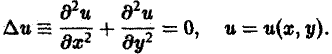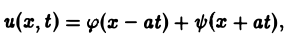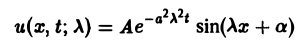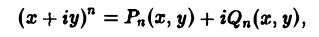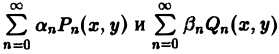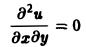Введение в теорию дифференциальных уравнений с частными производными (4 видео)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Содержание

Классификация уравнений с частными производными
Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения
Линейные дифференциальные уравнения с частными производными. Свойства их решений
Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными
Постановка основных задач для линейных дифференциальных уравнений второго порядка
Дифференциальные уравнения в частных производных, Масленникова В.Н., 1997
🔥 Видео

Видео:1.1. Введение в теорию дифференциальных уравненийСкачать

Классификация уравнений с частными производными

Задачи механики сплошной среды описываются системами дифференциальных уравнении с частными производными, для которых ставятся граничные и начальные условия — формулируются краевые задачи. Даже для уравнений, весьма схожих по форме записи, свойства решения могут существенно различаться. Поэтому особое внимание в теории уравнений с частными производными уделяется классификации — объединению их в типы или классы, внутри которых свойства решения и особенности постановки краевых задач являются сходными.

Рассмотрим классификацию на примере уравнения второго порядка с двумя независимыми переменными. Уравнения такого вида стали изучаться при математическом описании ряда физических задач, и этот раздел математики стал называться математической физикой, а линейные уравнения второго порядка с частными производными — уравнениями математической физики. Отметим, что лишь в частных случаях задачи движения газа или жидкости или задачи теплопроводности приводятся к уравнению подобного вида. Однако даже на этом простейшем примере проявляются практически все особенности, присущие и более сложным задачам.

Итак, рассмотрим дифференциальное уравнение с частными производными второго порядка (порядок дифференциального уравнения определяется порядком входящей в него старшей производной) с двумя независимыми переменными:

Если А, В, С — функции только х и у, а / — линейная функция своих аргументов и, ди/дх, ди/ду, то уравнение (1.1) является линейным. Для линейных уравнений развиты математические теории, позволяющие как делать общие качественные заключения о решении, так и строить методы решения. Во многих практических случаях оправданная система предположений и допущений позволяет привести математическую модель процесса к линейной системе или линейном>’ уравнению. В частности, линейным уравнением вида (1.1) описываются потенциальное течение жидкости, стационарное двумерное температурное поле, распространение волны в упругой среде и многие другие физические задачи, и оно изучено наиболее подробно. Но в большинстве случаев практические задачи описываются нелинейными уравнениями, общая теория которых еще не создана.

Если нелинейность уравнения состоит лишь в том, что коэффициенты А, В, С зависят от неизвестного решения и и (или) его младших производных (в данном случае — первых производных), то такая нелинейность локально не слишком сильно сказывается на решении по сравнению с линейным случаем. Уравнения с нелинейностями такого вида называются квазилинейными. Часто для анализа квазилинейных уравнений применяют метод «замораживания» коэффициентов, сводящий задачу к линейному случаю. Такой подход используется как для качественного анализа решения, так и для построения численных алгоритмов решения. Заметим, что задачи аэрогазодинамики описываются системой квазилинейных уравнений.

Уравнение (1.1) можно привести к эквивалентной системе дифференциальных уравнений первого порядка. Для этого введем обозначения для первых производных от искомой функции по независимым переменным р = ди/дх и q = ди/ду и запишем рассматриваемое уравнение, используя эти обозначения. В результате придем к системе трех уравнений первого порядка для трех неизвестных функций ц, р и q:

Заметим, что обратное действие (приведение системы уравнений первого порядка к одному уравнению) выполнимо нс всегда.

Одним из важнейших понятий в теории дифференциальных уравнений с частными производными является понятие о характеристиках. Впервые оно появилось в работах Г. Монжа при изучении уравнений, описывающих форму поверхностей.

Рис. 1.1. Задача Коши для уравнения второго порядка’

Для упрощения последующих выкладок введем следующие обозначения для вторых производных функции и :

Определим теперь задачу Коши для уравнения второго порядка. Пусть на линии у = у(х) заданы значения искомой функции и ее первых производных:

где а — естественная координата кривой. Поставим теперь следующую задачу: можно ли, зная значения функции и ее первых производных на кривой у(х), установить значения функции в точках, соседних с этой кривой? Поставленная задача называется задачей Коши для уравнения (1.1).

Для получения решения в точке Л/, соседней с кривой, можно воспользоваться разложением решения в ряд около некоторой точки О, лежащей на кривой задания начальных данных у(х). Такое разложение имеет вид

Заметим, что в этом разложении нельзя ограничиваться только линейными членами — обязательно присутствие вторых производных. Это связано с тем, что исходное дифференциальное уравнение накладывает связи именно на вторые производные. Если мы опустим их в разложении (1.2), то будет потеряно все физическое содержание рассматриваемого явления, в котором именно взаимосвязь вторых производных (своего рода «кривизн») определяет сущность описываемого процесса.

Использование данного выражения для получения решения в точке М связано с возможностью определения производных, в него входящих. Первые производные известны из начальных условий, заданных на кривой начальных данных. Вторые же необходимо каким- либо способом определить, после чего выражение (1.2) может быть использовано для получения решения в точке М. Можно показать, что после определения вторых производных высшие производные также могут быть вычислены, и таким образом будет решен вопрос о повышении точности выражения (1.2) за счет увеличения количества членов разложения.

Для определения вторых производных мы можем использовать данные, заданные на кривой. Приращения первых производных вдоль кривой запишутся следующим образом:

Заметим, что в этих выражениях dx и dy являются взаимосвязанными и их отношение определяется угловым коэффициентом кривой dy/dx = у'(х).

К этим двум выражениям, связывающим три неизвестные вторые производные, необходимо добавить исходное дифференциальное уравнение, что позволит получить линейную систему для значений вторых производных в точке М кривой у(х):

Вопрос об определении вторых производных и, тем самым, о восстановлении решения в точках, прилежащих к кривой начальных данных, связан с возможностью решения линейной системы (1.3). Если определитель этой системы не равен нулю, то она имеет единственное решение, производные г, s, t и выражение (1.2) может использоваться для прогноза решения в точках области, лежащих вне линии начальных данных у = у(х).

В том же случае, когда определитель системы (1.3) обращается в ноль:

система линейных уравнений становится вырожденной, не допускающей определения вторых производных. Если решение найти не удастся, то принципиально нельзя будет сместиться от кривой начальных данных в соседние точки области.

Раскрывая определитель (1.4), получим условие обращения его в ноль:

которое можно записать в виде дифференциального уравнения в разрешенном относительно производной dy/dx виде:

Из этого соотношения видно, что исходная задача становится неразрешимой, если угловой коэффициент кривой принимает некоторое особое значение, выражаемое через коэффициенты исходного дифференциального уравнения. Это особое направление называется характеристическим, а кривая, касательная к которой в каждой точке принимает характеристическое направление, — характеристикой дифференциального уравнения с частными производными. Как видим, обыкновенное дифференциальное уравнение (1.5) определяет поле характеристических направлений, а его интеграл определяет характеристические линии.

Если эти кривые используются как линии задания начальных данных, то решение не может быть продолжено в соседние точки области, поэтому такие кривые имеют огромное значение при анализе свойств дифференциальных уравнений и при построении расчетных алгоритмов их решения.

В основу классификации уравнения (1.1) положено наличие у него характеристик. Как видно из (1.5), исходное уравнение в каждой точке области своего определения может иметь либо два характеристических направления, либо одно, либо вообще не иметь характеристик. Определяющим в этом вопросе является знак дискриминанта уравнения — подкоренного выражения В 2 — АС.

Если В 2 — АС 2 — АС = О, то имеется одно семейство характеристик. В этом случае говорят, что уравнение (1.1) является параболическим. или принадлежит к параболическому типу.

Если В 2 — АС > 0, то имеются два различных семейства характеристик и уравнение (1.1) является гиперболическим или принадлежит к гиперболическому типу.

Так как тип уравнения связан со значениями коэффициентов дифференциального уравнения, то уравнение с переменными коэффициентами в разных частях области определения может принадлежать к различным типам. Такие уравнения называют уравнениями смешанного типа.

На первый взгляд представляется странным, почему для определения типа дифференциального уравнения используется терминология, относящаяся к коническим сечениям — алгебраическим кривым второго порядка: эллипсу, параболе и гиперболе. Связь состоит в том, что фундаментальную роль в теории уравнений вида (1.1) играет особым образом построенное алгебраическое выражение квадратичная форма, коэффициентами которой являются коэффициенты исходного уравнения. Для уравнения (1.1) она имеет вид Ах 2 +2Вху+Су 2 и может быть приведена к канонической форме, которая будет, в зависимости от значений коэффициентов, принимать вид эллипса, параболы или гиперболы, что и объясняет используемую терминологию.

Заметим, что для классификации мы использовали линейное уравнение второго порядка, однако характеристический анализ применяется и к другим уравнениям и системам.

Аналогичные соображения закладываются в основу классификации систем дифференциальных уравнений, которая строится на основе характеристических свойств — начПичия полного набора характеристик (гиперболические системы) или отсутствия действительных характеристик (эллиптические системы). Тип уравнения определяет общий характер его решения, зависимость решения от входных данных и, как следствие этого, методы получения численных решений краевых задач. В нашем курсе мы неоднократно будем возвращаться к анализу характеристических свойств изучаемых математических моделей механики сплошной среды.

Сделаем несколько замечаний, на которые мы не обращали внимание ранее.

Замечание 1. Инвариантность характеристических направлений. Можно доказать, что характеристики остаются инвариантными при преобразованиях независимых переменных. То есть характеристические направления не зависят от выбора системы координат, в которой мы записываем исходное уравнение, и от различных преобразований независимых переменных. Эти направления определяются только свойствами самого изучаемого явления, которое описывается своей математической моделью дифференциальным уравнением. В этом смысле характеристики определяют некоторые особые направления в пространстве — «собственные» направления данной задачи. Особо отметим, что определить характеристические направления удалось из анализа дифференциального уравнения. Поэтому получение характеристических направлений связано с записью математической модели в форме дифференциального уравнения (в дальнейшем мы увидим, что существуют и другие формы записи математических моделей, например в форме интегральных соотношений).

Замечание 2. Определение старших производных. В построенном нами примере для продолжения решения в точки, соседние с линией задания начальных данных, использовались производные до второго порядка включительно. Покажем, что если в качестве линии начальных данных используется нехарактеристическая кривая, го точность соотношения можно сколь угодно повышать, вычисляя старшие производные решения и таким образом продолжая ряд.

Для начала рассмотрим вопрос об определении третьих производных, которые обозначим соответственно Q = u_xxx, R = u_xxy, S = = и_хуу, Т = и_ууу. Так как, по условию, кривая не является характеристикой, то на основе предыдущего анализа на кривой начальных данных у(х) в дополнение к заданным из начальных условий значениям м, р, q вычислены и вторые производные г, .s, t. Поэтому для третьих производных можно выписать систему соотношений, определяющих их из дифференциалов вторых производных вдоль линии у(х) :

Добавив к этой системе исходное уравнение (1.1), продифференцированное по х, получим линейную систему

Легко убедиться, что она имеет то же условие невырожденности, что и система линейных уравнений при анализе характеристик.

Для этого при вычислении определителя матрицы проведем его разложение но элементам последнего столбца. Определитель третьего порядка, стоящий при единственном ненулевом элементе, будет совпадать с определителем матрицы в задаче анализа характеристик.

Таким образом, для любой нехарактеристической кривой третьи производные решения находятся из данных, заданных на этой кривой. Продолжая таким образом, можно находить следующие старшие члены разложения и тем самым повышать порядок точности представления решения.

Замечание 3. Условия совместности на характеристиках. В

том случае если для уравнения (1.1) определена характеристика, то на приращения производных от решения р, q вдоль кривой накладываются дополнительные условия. Действительно, равенство нулю определителя (1.4) означает линейную зависимость уравнений, входящих в (1.3). Из линейной алгебры известно, что для разрешимости вырожденной системы необходимо, чтобы ранг системы был равен рангу ее расширенной матрицы. Другими словами, требуется, чтобы все определители третьего порядка расширенной матрицы

были равны нулю. Нетрудно показать, что эго условие, совместно с полученным ранее соотношением для характеристик (1-5), приводит к следующим двум условиям, которые должны выполняться вдоль характеристик:

Эти условия называются условиями на характеристиках или условиями coeAiecmnocmu. Они играют большую роль как при изучении качественных свойств решения, так и при построении алгоритмов численного решения задач.

1 1асто гиперболическую задачу удобно формулировать через набор ее характеристик и дифференциальные соотношения совместности, справедливые на этих характеристиках. Заметим, что в случае двух независимых переменных задача трансформируется в систему обыкновенных уравнений, определяющих характеристические кривые, и обыкновенных дифференциальных уравнений, соответствующих условиям совместности.

Замечание 4. Физический смысл характеристик. В уравнениях, в которых в качестве независимых выступают пространственные переменные, характеристики определяют область влияния точек. Известные из газодинамики сверхзвуковых стационарных течений конус Маха и линия Маха относятся к такому кругу понятий.

Если в качестве одной из независимых переменных — переменной гиперболичности — выступает время, характеристики выражают конечность скорости распространения сигнала и управляют таким образом причинно-следственными отношениями в рассматриваемой системе. С характеристиками в этом случае тесно связана возможность распространения волн с конечной скоростью.

Приведем примеры дифференциальных уравнений различных типов.

Пр и м е р 1. Уравнение Пуассона>:

Если / = 0, то это уравнение называют уравнением Лапласа. Здесь А = С = 1, В = О, В 2 — АС = —1, т.е. это уравнение эллиптического типа, часто встречающееся в физических приложениях. Им описываются задачи потенциального движения жидкости, фильтрации в пористых телах, задачи магнито- и электростатики, стационарное распределение температур в теле, распределение напряжений в некоторых задачах линейной теории упругости и т. д.

Уравнению Лапласа эквивалентна следующая простейшая эллиптическая система Даламбера Эйлера (иногда эти уравнения называют уравнениями Коши Римана):

Уравнение Лапласа может быть распространено на случай трех (или более) независимых переменных:

1 Пуассон Симеон Дени (Poisson S.D., 1781-1840) — французский математик, физик и механик. Его работы сыграли важную роль в становлении современной науки: в теории вероятностей, математической физике, теории упругости и гидромеханике. Упомянутое уравнение было выведено Пуассоном при исследовании ряда задач теории гравитационного притяжения (мемуар «О притяжении сфероидов», 1835).

Дифференциальный оператор Д = д 2 /дх 2 + д 2 /ду 2 + д 2 /дг 2 называют оператором Лапласа.

Пример 2. Уравнение теплопроводности. Одномерное нестационарное температурное поле в среде с постоянными теплофизическими характеристиками описывается уравнением

в котором коэффициент температуропроводности а должен удовлетворять условию а > 0.

Здесь вместо переменной у введена переменная t — время, соответствующая физическому содержанию описываемых уравнением задач. Коэффициенты, входящие в уравнение, равны: А = 1, В = 0, С = 0, В 2 — АС = 0, т.е. эго уравнение параболического типа. Такими уравнениями описываются нестационарное распределение температур в задачах теплопроводности, диффузия инертной примеси, распространение электромагнитных волн в проводящих средах, движение вязкой жидкости в пограничном слое тела и т. д.

II р и м е р 3. Волновое уравнение. Распространение плоской волны с постоянной скоростью со в изотропной среде описывается линейным одномерным волновым уравнением

в котором ось х соответствует направлению распространения волны.

Здесь А = Cq, С = 1, В = 0, это уравнение гиперболического типа. Примером простейшей гиперболической системы является эквивалентная (1.11) система

Уравнения такого типа описывают распространение колебаний в сплошных средах, электромагнитные колебания, сверхзвуковое течение идеального газа.

Приведенные выше примеры демонстрируют три основных типа уравнений математической физики. Различие в них связано с различием описываемых ими физических процессов. Уравнения параболического и гиперболического типов описывают неустановившийся процесс. Это означает, что на решение в момент времени t влияет состояние в предыдущие моменты времени, но никак не могут влиять последующие события. Уравнения гиперболического типа могут описывать и установившиеся процессы, в этом случае краевое условие влияет па решение только в одну сторону (по отношению к переменной, являющейся аналогом времени), а одна из пространственных координат является аналогом времени. Примером такой гиперболической задачи может служить сверхзвуковое, установившееся движение газа. Таким образом, параболические и гиперболические уравнения связаны с областями, «открытыми»в одном направлении, а соответствующая этому направлению независимая переменная является аналогом времени.

В случае же эллиптических задач на решение в некоторой точке области влияют краевые условия, заданные на всей замкнутой границе области.

Видео:Линейные дифференциальные уравнения в частных производныхСкачать

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

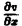
где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Видео:Введение в теорию гамильтоновых уравнений в частных производных 1Скачать

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 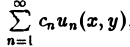, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 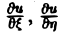и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 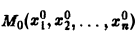и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 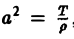где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 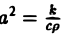где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

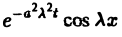
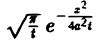
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения в частных производных, Масленникова В.Н., 1997

Дифференциальные уравнения в частных производных, Масленникова В.Н., 1997.

Учебник написан на основе лекций, читаемых автором на факультете физико-математических и естественных наук Российского университета дружбы народов.

В книге отражены следующие темы: выводы основных уравнений математической физики и гидродинамики; общая теория дифференциальных уравнений в частных производных, включая теорему Ковалевской, характеристики, классификацию уравнений и систем; даны основы теории обобщенных функций и пространств Соболева, с использованием которых изучены задачи Коши, краевые и начально-краевые задачи, в том числе задача на собственные значения для эллиптического уравнения второго порядка с переменными коэффициентами. Изложены приближенный метод Галеркина и свойства гармонических функций.

ОГЛАВЛЕНИЕ
Введение
ГЛАВА I. ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Введение. Основные определения
1. Суть предмета
2. Основные определения в теории уравнении с частными производными
3. Примеры уравнений в частных производных
4. Из истории предмета
§ 2. Некоторые математические модели физических процессов
1. Вывод уравнения теплопроводности; граничные и начальные условия
2. Вывод уравнения равновесия мембраны и граничных условий
3. Вывод уравнения колебаний мембраны. Начальные и граничные условия
4. Частная и полная производные вектора и скаляра. Вывод уравнения неразрывности сплошной среды
5. Уравнения движения сплошной среды
6. Вывод уравнения звуковых волн (волнового уравнения)
§ 3. О постановке краевых задач математической физики
ГЛАВА II. НЕКОТОРЫЕ ВОПРОСЫ ОБЩЕЙ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Задача Коши. Теорема Ковалевской
1. Определение системы типа Ковалевской. Примеры. Постановка задачи Копта для общей нелинейной системы уравнений в частных производных типа Ковалевской
2. Определение аналитической функции многих действительных переменных. Формулировка теоремы Ковалевской о единственности и локальной разрешимости задачи Коши в классе аналитических функций для нелинейных систем типа Ковалевской
3. Доказательство теоремы Ковалевской для линейных систем первого порядка
а. Доказательство единственности аналитического решения
б. Мажоранты аналитической функции и их построение
в. Доказательство существования аналитического решения; неравенства между коэффициентами данной и мажорирующей систем; построение явного решения мажорирующей системы
4. Некоторые замечания к теореме Ковалевской
г. Об области существования аналитического решения
д. Пример уравнения теплопроводности, для которого не существует аналитического решения задачи Коши в окрестности точки .
е. Примеры локально неразрешимых уравнений.
§ 2. Задача Коши с начальными данными на произвольной поверхности. Возмоишость ее сведения к задаче Коши с начальными данными на гиперплоскости
§ 3. Характеристики и характеристические направления. Особенности постановки задачи Коши с начальными данными на характеристиках
1. Определение характеристической поверхности (характеристики) для уравнения в частных производных.
Примеры
2. Особенности постановки задачи Коши с начальными данными на характеристиках
3. Характеристические направления. Определение характеристик с помощью характеристических направлений. Примеры
4. Характеристики и характеристические направления для линейных систем произвольного порядка .
§ 4. Классификация уравнений и систем уравнений в частных производных. Определение эллиптических, гиперболических и параболических по Петровскому линейных уравнений и систем произвольного порядка. Системы эллиптические по Дугласу — Ниренбергу. Примеры .
§ 5. Приведение уравнения второго порядка от многих независимых переменных к каноническому виду в фиксированной точке. Классификация .
§ 6. Приведение уравнения второго порядка на плоскости к каноническому виду. Еще раз о типах уравнений
§ 7. Преобразования Фурье и Лапласа.
Определение пространства S. Преобразование Фурье функций из S .
§ 8. Определение корректности постановки задачи Коши
§ 9. Условие некорректной постановки задачи Кохпи в терминах корней характеристического многочлена. Лемма об экспоненциальном решении. Определение обобщенно однородного многочлена. Основная теорема. Примеры .
ГЛАВА III. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ. ОБОБЩЕННЫЕ ФУНКЦИИ И ИХ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ РЕШЕНИЯ
§ 1. Решение задачи Кошн для уравнения теплопроводности методом преобразования Фурье с начальными данными из S.
Преобразование Фурье на L(R ) и на L2(-Rn)
§ 2. Понятие обобщенной функции, ее физический смысл. Определение ^-функции Дирака. Пространство основных функций V и пространство обобщенных функций V
§ 3. Определение пространства обобщенных функций 5′. Преобразование Фурье обобщенных функций из 5′ .
§ 4. Свертка двух функций: ><х) € 5, д(х) € С*. Теорема о свертке .
§ 5. Применение теоремы о свертке к решению задачи Кошн для уравнения теплопроводности. Вычисление ядра Пуассона
§ 6. Свойства ядра Пуассона .
§ 7. Решение задачи Кошн для уравнения теплопроводности с непрерывной ограниченной начальной функцией .
§ 8. Задача Кошн для неоднородного уравнения теплопроводности. Принцип Дюамеля
§ 9. Принцип максимума для решения уравнения теплопроводности .
1. Принцип максимума для ограниченной области. Следствия: единственность решения первой начально-краевой задачи и непрерывная зависимость его от краевых и начальных значений
2. Принцип максимума для полосы.
Следствия: единственность решения задачи Коти и непрерывная зависимость его от начальных данных. Корректность постановки задачи Коши для уравнения теплопроводности .
ГЛАВА IV. ЗАДАЧА КОШИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ. ПРИМЕНЕНИЕ ОБОБЩЕННЫХ ФУНКЦИИ К ИССЛЕДОВАНИЮ РЕШЕНИЯ
§ 1. Вывод энергетического неравенства для волнового уравнения. Следствия: теорема единственности решения задачи Коши и непрерывная зависимость его от начальных данных; область единственности .
§ 2. Решение задачи Коши для волнового уравнения при начальных данных, принадлежащих пространству S
§ 3. Функция, сосредоточенная на сфере. Преобразование Фурье ^-функции, сосредоточенной на сфере. Теорема о свертке обобщенной функции из 5′ с компактным носителем и функции из S .
§ 4. Вывод формулы Кирхгофа для решения задачи Коши для волнового уравнения в случае трех пространственных переменных
§ 5. Вывод формулы Пуассона для решения задачи Коши для волнового уравнения в случае двух пространственных переменных. Метод спуска.
Формула Даламбера для уравнения колебания струны .
§ 6. Корректность постановки задачи Коши для волнового уравнения.
§ 7. Решение задачи Коши для неоднородного волнового уравнения .
§ 8. Фундаментальное решение (функция Грина) задачи Коши для волнового уравнения .
§ 9. Качественные свойства решения задачи Коши для волнового уравнения. Распространение волн .
1. Область зависимости решения задачи Коши. Конечность скорости распространения возмущений. Область влияния
2. Распространение волн в случае трех пространственных переменных. Принцип Гюйгенса.
3. Распространение волн на плоскости и в случае одного пространственного переменного. Диффузия волн
ГЛАВА V. ОСНОВНЫЕ НАЧАЛЬНО-КРАЕВЫЕ ЗАДАЧИ ДЛЯ НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ (предварительные рассмотрения)
Введение.
§ 1. Начально-краевые задачи для гиперболического уравнения второго
порядка. Энергетические оценки. Интеграл энергии. Теоремы единственности и непрерывной зависимости
§ 2. Метод разделения переменных (метод Фурье) для уравнения колебания струны. Сходимость рядов, определяющих классическое решение
§ 3. Начально-краевые задачи для параболического уравнения второго порядка. Энергетическая оценка. Теоремы единственности и непрерывной зависимости
§ 4. Метод разделения переменных для решения первой начально-краевой задачи для уравнения теплопроводности; сходимость рядов, определяющих классическое решение
§ 5. Метод Фурье для уравнении с переменными коэффициентами. Предварительные рассмотрения .
§ 6. О линейных ограниченных и неограниченных опраторах в гильбертовом пространстве .
ГЛАВА VI. ОБОБЩЕННЫЕ ПРОИЗВОДНЫЕ, ПРОСТРАНСТВА СОБОЛЕВА, ОБОБЩЕННЫЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Обобщенные решения дифференциальных уравнений. Два способа введения обобщенного решения
§ 2. Обобщенные производные в смысле
Соболева и их основные свойства ,
§ 3. Пространство Соболева W<Q) и его полнота.
§ 4. Пространство Соболева W'(J?).
§ 5. Пространство Соболева W<ft) и его эквивалентная норшгровка. Неравенство Фридрихса.
§ 6. Средние функции, их свойства: бесконечная дифференцируемость, сходимость в норме L перестановочность операций дифференцирования и усреднения. Ядро усреднения и его свойства
§ 7. Граничные свойства функций из пространств Соболева W(Q) в W><f2). Формула интегрирования по частям
§ 8. Основные понятия о продолжения функций из пространств Соболева на более широкую область с сохранением класса
§ 9. Неравенство Пуанкаре
§ 10. Компактность вложения ограниченного множества из W% (Л) в Li(Q)
§ 11. Обобщенные решения основных краевых задач для эллиптического уравнения второго порядка
ГЛАВА VII. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ И МЕТОД ФУРЬЕ (продолжение) В ПРОСТРАНСТВАХ СОБОЛЕВА
§ 1. Задачи на собственные значения для эллиптического уравнения. Обобщенные собственные функции задач Дирихле, Неймана и третьей краевой задачи. Сведение задач на собственные значения к операторному уравнению с самосопряженным вполне непрерывным оператором .
§ 2. Свойства собственных значений и обобщенных собственных функций для эллиптического оператора. Основная теорема
§ 3. Вариационный принцип собственных значений и собственных функций. О точной постоянной в неравенстве Фридрихса
§ 4. Обоснование метода Фурье для гиперболического уравнения в пространстве Соболева
ГЛАВА VIII. МЕТОД ГАЛЕРКИНА ДЛЯ НАХОЖДЕНИЯ ПРИБЛИЖЕННЫХ РЕШЕНИЙ
§ 1. Метод Галеркина для приближенного обобщенного решения задачи Дирихле для уравнения Пуассона
§ 2. Метод Галеркина для приближенного решения первой начально-краевой задачи для уравнения теплопроводности. Теорема единственности обобщенного решения .
ГЛАВА IX. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ФУНКЦИЯ ГРИНА
§ 1. Определение фундаментального решения для произвольного линейного дифференциального уравнения и его построение методом преобразования Фурье. Фундаментальное решение для оператора Лапласа
§ 2. Решение дифференциальных уравнений с постоянными коэффициентами во всем пространстве в виде свертки с помощью фундаментального решения
§ 3. Формула Грина для оператора Лапласа .
§ 4. Функция Грина в задаче Дирихле для
оператора Лапласа. Представление решения задачи Дирихле для уравнения Пуассона через функцию Грина. Ньютонов потенциал, потенциалы простого и двойного слоя. Свойства функции Грина
ГЛАВА X. ГАРМОНИЧЕСКИЕ ФУНКЦИИ И ИХ СВОЙСТВА
§ 1. Примеры и физический смысл
гармонических функций .
§ 2. Слабый принцип максимума для гармонических функций и его следствия
§ 3. Лемма Жиро (о знаке производной в граничной точке для гармонической в шаре функции)
§ 4. Строгий принцип максимума для гармонических функций и его следствия
§ 5. Теорема о знаке производной в граничной точке гармонической в области функции и ее следствия (теоремы единственности) .
§ 6. Дальнейшие свойства гармонических функций: теорема о потоке тепла, необходимое условие разрешимости задачи Неймана для уравнения Лапласа и Пуассона, теоремы о среднем по сфере и шару, бесконечная дифференцируемость гармонических функций внутри области
§ 7. Вывод формулы Пуассона для решения задачи Дирихле для уравнения Лапласа в шаре с непрерывной граничной функцией .
§ 8. Свойства гармонических функций: теорема Гарнака о равномерно сходящейся последовательности гармонических функций, неравенства Гарнака, теорема Лиувилля и теорема об устранимой особенности
§ 9. Внешние краевые задачи для уравнения Лапласа
1. Постановка внешней задачи Дирихле в случае п > 3, теорема единственности .
2. Постановка внешней задачи Дирихле в плоском случае .
3. Сведение решения внешней задачи Дирихле к решению задачи Дирихле для ограниченной области. Преобразование Кельвина ,
4. Внешняя задача Неймана
ГЛАВА XI. ДОПОЛНЕНИЕ. ОБЩИЕ ТЕОРЕМЫ ВЛОЖЕНИЯ ДЛЯ КЛАССОВ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
§ 1. Основные определения и формулировка основных теорем вложения .
§ 2. Вспомогательные теоремы о продолжении функций с J на все А и о плотности
финитных функций С°°(ДП) в WfrRn) .
§ 3. Теоремы Вложения для дифференцируемых функций, заданных во всем пространстве R .
1. Формулировка теорем вложения
2. Бесселевы потенциалы
3. Доказательство теорем вложения для функции многих переменных, заданных во всем пространстве
§ 4. Доказательство теорем вложения для
функций, заданных в области .
Литература.
Предметный указатель

Классификация уравнений и систем уравнений в частных производных.Определение эллиптических, гиперболических и параболических по Петровскому линейных уравнений и систем произвольного порядка. Системы, эллиптичесикие по Дуглису — Ниренбергу.
Основные результаты по классификации уравнений высокого порядка и систем уравнений в частных производных принадлежит И.Г.Петровскому.
Классификация имеет большое значение для теории уравнений в частных производных, так как принадлежность уравнения к тому этого уравнения и постановке для него краевых задач.
Отметим, однако, что при классификации выделяются только три наиболее важных типа уравнений и систем: эллиптические, гиперболические и параболические. В то же время значительно большая часть уравнении и систем уравнений в частных производных не принадлежат ни к одному из этих трех типов. Таковыми, например, являются очень важные в приложениях системы гидродинамики, приведенные нами в § 2 главы I.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Дифференциальные уравнения в частных производных, Масленникова В.Н., 1997 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу