Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Видео:ГМТ // ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКСкачать
Геометрическое место точек
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Понятие ГМТ часто используют при решении задач на построение.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Уравнение геометрического места точек равноудаленных от точки и плоскости
| Учебный курс | Решаем задачи по геометрии |
Видео:найти уравнение геометрического места точекСкачать  Геометрическое место точек. Метод геометрических местОпределение: Геометрическим местом точек называется геометрическая фигура на плоскости, каждая точка которой обладает одним и тем же определенным свойством. Метод геометрических мест применяется чаще всего при построениях. Например, серединный перпендикуляр к отрезку можно определить как геометрическое место точек, равноудаленных от точек концов отрезков; окружность можно определить как геометрическое место точек, равноудаленных от данной точки. Теорема (о геометрическом месте точек). Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная отрезку, соединяющему эти точки, и проходящая через его середину.
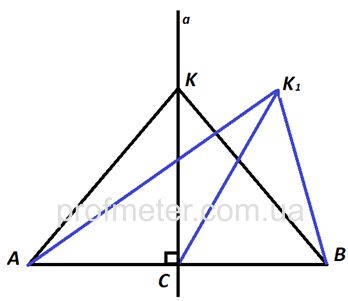
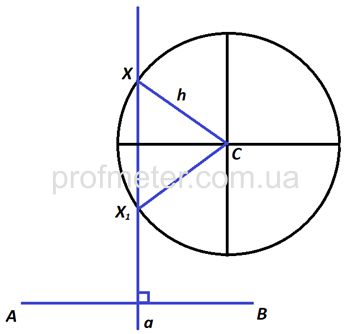
Доказательство. Пусть даны точки А и В, а точка С – середина отрезка АВ. Нужно найти геометрическое место точек, равноудаленных от точек А и В. Доказательство основано на свойстве серединного перпендикуляра к отрезку. Серединный перпендикуляр СК, принадлежащий прямой а, как и любая точка этой прямой, — есть геометрическое место точек, равноудаленных от А и В, так как СКꓕАВ. Допустим, что есть еще точка К1, расстояние до которой от А и В одинаково. Рассмотрим ∆АК1В, он разбит отрезком К1С на два треугольника: ∆АК1С и ∆К1СВ. Если эти треугольники равны, то точка К1 тоже удалена на одинаковое расстояние от А и В. Через точку С проходят две прямые СК и СК1. На основании теоремы 16 (о единственности перпендикуляра из точки к прямой), если СКꓕАВ по построению, то СК1 не может быть перпендикулярна АВ. Метод геометрических местПостроить точку Х, равноудаленную от А и В и находящуюся на расстоянии h от точки С.
1.Построим геометрическое место точек, удовлетворяющее первому условию: это будет серединный перпендикуляр к отрезку АВ. Прямая а, которая содержит серединный перпендикуляр к отрезку АВ, удовлетворяет полностью первому условию. 2.На перпендикуляре (прямая а) должна находится точка Х, которая удовлетворяла бы второму условию (расстояние от нее до С должно составлять h). Если из точки С радиусом h провести окружность, то все точки окружности будут расположены от С на одинаковом расстоянии h (построили второе геометрическое место точек, равноудаленных от С). 3.Пересечение первого геометрического места точек (прямая а) и второго (окружности с центром в точке С) будет удовлетворять обоим условиям задачи. Точки пересечения окружности и прямой (Х1 и Х) и будут теми искомыми точками, которые равноудалены от точек А и В и находятся от С на расстоянии h. 📹 ВидеоУравнение плоскости. 11 класс.Скачать  Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать  ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЕННЫХ ОТ КОНЦОВ ОТРЕЗКА. Задачи на ГМТ | ГЕОМЕТРИЯ 7 классСкачать  Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать  Уравнения стороны треугольника и медианыСкачать  Вышнепольский В.И. "Геометрические места точек, равноудаленных от плоскости и сферы"Скачать  №949. На оси абсцисс найдите точку, равноудаленную от точек: а) А (1; 2)Скачать  ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЕННЫХ ОТ ТРЕХ ДАННЫХ ТОЧЕК. Задачи. Метод ГМТ. ГЕОМЕТРИЯ 7 классСкачать  Составляем уравнение прямой по точкамСкачать  PRO геометрические места точекСкачать  Точка, равноудаленная от всех сторон многоугольникаСкачать  Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать  9 класс, 7 урок, Уравнение прямойСкачать  №948. На оси ординат найдите точку, равноудаленную от точек: а) А (-3; 5)Скачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЕННЫХ ОТ СТОРОН УГЛА. Задачи на ГМТ | ГЕОМЕТРИЯ 7 классСкачать  |
