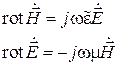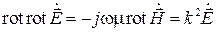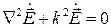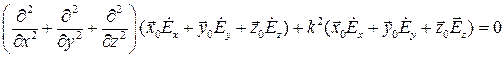Уравнение гельмгольца для электромагнитного поля (3 видео)

Содержание

Уравнения Гельмгольца. Волновой характер электромагнитного поля
Уравнения Гельмгольца электромагнитных волн в гиперболически намагниченных гиротпропных эллиптических волноводах Текст научной статьи по специальности « Физика»
Аннотация научной статьи по физике, автор научной работы — Итигилов Гарма Борисович, Ширапов Дашадондок Шагдарович, Сажин Виктор Иванович
Похожие темы научных работ по физике , автор научной работы — Итигилов Гарма Борисович, Ширапов Дашадондок Шагдарович, Сажин Виктор Иванович
Helmholtz equations of electromagnetic waves in hyperbolic the magnetized gyrotropic elliptic wave guides
Текст научной работы на тему «Уравнения Гельмгольца электромагнитных волн в гиперболически намагниченных гиротпропных эллиптических волноводах»
📸 Видео

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Уравнения Гельмгольца. Волновой характер электромагнитного поля

Одним из важнейших результатов, полученных Максвеллом, явилось доказательство волновой природы электромагнитного поля. Уже упоминалось о том, что изменение во времени электрического поля приводит к возникновению магнитного поля, неоднородного в пространстве, и наоборот. Физическая картина здесь напоминает процесс обмена энергией между электрическим и магнитным полем в обычном колебательном контуре. Поэтому можно ожидать, что электромагнитный процесс в самом общем случае представляет собой также некоторые колебания. Принципиальная разница здесь заключается в том, что колебания электромагнитного поля должны рассматриваться одновременно во всех точках пространства. В физике колебательное движение непрерывной среды принято называть волновым процессом.

Докажем волновой характер электромагнитного поля математически, сведя уравнения Максвелла к другим уравнениям, которые заведомо описывают волновой процесс.

Рассмотрим электромагнитное поле в некоторой области пространства, где плотность зарядов отсутствует, т.е. 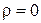. Плотность сторонних электрических токов также предполагается равной нулю.

Выпишем первые два уравнения из общей системы уравнений Максвелла для комплексных амплитуд в виде:

Эти два уравнения могут быть сведены к одному. Для этого применим операцию rot к левой и правой частям второго уравнения, а затем выразим полученную правую часть через второе уравнение:

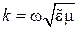
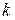
Здесь − в общем случае комплексное число, являющееся, как будет показано, постоянной распространения электромагнитной волны. В литературе для величины можно встретить также названия фазовая постоянная или волновое число.

Дальнейшее преобразование формулы можно осуществить, если воспользоваться известным тождеством векторного анализа:

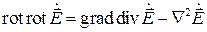
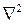
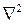
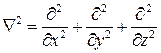
Здесь (набла квадрат) − векторный дифференциальный оператор второго порядка, конкретная форма которого полностью определяется той координатной системой, в которой производятся вычисления. Для декартовой системы координат действие оператора сводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа

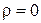
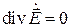
Если воспользоваться законом Гаусса, который в соответствии с принятым условием обеспечивает , то уравнение может быть переписано в следующем простом виде:

Пользуясь симметрией уравнений Максвелла, совершенно аналогично получаем также уравнение относительно векторного поля :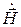

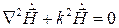
Эти два уравнения в математической физике носят название уравнений Гельмгольца. Математически можно показать, что эти уравнения описывают стационарные волновые процессы, т.е., распространение в пространстве волн с некоторой постоянной частотой.

Таким образом, получен фундаментальный вывод теории Максвелла − переменность во времени электрических или магнитных полей приводит к распространению в пространстве электромагнитных волн.

В координатной форме уравнения Гельмгольца записываются следующим образом

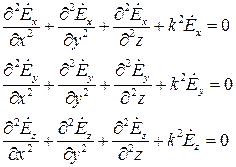
Решение такой системы значительно упрощается в тех частных случаях, когда поле не имеет каких-либо составляющих, например, 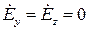, а также тогда, когда поле постоянно в каких-либо плоскостях, например .

Дата добавления: 2015-10-19 ; просмотров: 1857 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Уравнения Гельмгольца электромагнитных волн в гиперболически намагниченных гиротпропных эллиптических волноводах Текст научной статьи по специальности « Физика»

Видео:4.1 Однородные волновые уравнения ГельмгольцаСкачать

Аннотация научной статьи по физике, автор научной работы — Итигилов Гарма Борисович, Ширапов Дашадондок Шагдарович, Сажин Виктор Иванович

Получены обобщенные уравнения Гельмгольца электромагнитных волн в регулярных волноводах с ортогональными формами поперечного сечения, заполненных намагниченным ферритом (гиротропной средой). Рассматривается один из двух случаев поперечного намагничивания феррита, когда направление распространение электромагнитной волны и направление внешнего намагничивающего постоянного магнитного поля перпендикулярны, а именно нормальное намагничивание. Математической основой является модифицированный метод инвариантных преобразований, позволяющий легко осуществить переход к любому регулярному волноводу с прямолинейной и криволинейной ортогональной формой поперечного сечения: прямоугольному, круглому, эллиптическому. На базе полученных выражений впервые выведены уравнения Гельмгольца для наименее исследованных гиротропных эллиптических волноводов при нормальном (гиперболическом) намагничивании. Представленные уравнения Гельмгольца позволяют поставить и решить краевую задачу эллиптического волновода при гиперболическом намагничивании с дальнейшим получением дисперсионного уравнения.

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Helmholtz equations of electromagnetic waves in hyperbolic the magnetized gyrotropic elliptic wave guides

The generalized equations of Helmholtz of electromagnetic waves in the regular wave guides with orthogonal forms of a transverse section filled with the magnetized ferrite (the gyrotropic environment) are received. One of two cases of cross magnetization of ferrite when the direction distribution of electromagnetic wave and the direction of the outside magnetizing constant magnetic field are perpendicular is considered, namely normal magnetization. A mathematical basis is the modified method of invariant conversions allowing to realize easily transition to any regular wave guide with the rectilinear and curvilinear orthogonal form of a transverse section: rectangular, round, elliptic. On the basis of the received expressions Helmholtz equations for the least probed gyrotropic elliptic wave guides for the first time are removed in case of normal (hyperbolic) magnetization. The provided Helmholtz equations allow to deliver and solve a boundary value problem of an elliptic wave guide in case of hyperbolic magnetization with further receiving the dispersing equation.

Видео:Билет №34 "Электромагнитные волны"Скачать

Текст научной работы на тему «Уравнения Гельмгольца электромагнитных волн в гиперболически намагниченных гиротпропных эллиптических волноводах»

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ОБРАБОТКА ДАННЫХ

О Г. Б. Итигилов, Д. Ш. Ширапов, В. И. Сажин

Уравнения Гельмгольца электромагнитных волн в гиперболически намагниченных гиротпропных эллиптических волноводах

Получены обобщенные уравнения Гельмгольца электромагнитных волн в регулярных волноводах с ортогональными формами поперечного сечения, заполненных намагниченным ферритом (гиротропной средой). Рассматривается один из двух случаев поперечного намагничивания феррита, когда направление распространение электромагнитной волны и направление внешнего намагничивающего постоянного магнитного поля перпендикулярны, а именно — нормальное намагничивание. Математической основой является модифицированный метод инвариантных преобразований, позволяющий легко осуществить переход к любому регулярному волноводу с прямолинейной и криволинейной ортогональной формой поперечного сечения: прямоугольному, круглому, эллиптическому. На базе полученных выражений впервые выведены уравнения Гельмгольца для наименее исследованных гиротропных эллиптических волноводов при нормальном (гиперболическом) намагничивании. Представленные уравнения Гельмгольца позволяют поставить и решить краевую задачу эллиптического волновода при гиперболическом намагничивании с дальнейшим получением дисперсионного уравнения.

Ключевые слова: произвольное намагничивание, тензор магнитной проницаемости феррита, поперечные компоненты электромагнитной волны, коэффициенты Ламэ, символы Кристоффеля.

О G. B.Itigilov, D. Sh. Shirapov, V. I. Sazhin

Helmholtz equations of electromagnetic waves in hyperbolic the magnetized gyrotropic elliptic wave guides

On the basis of the received expressions Helmholtz equations for the least probed gyrotropic elliptic wave guides for the first time are removed in case of normal (hyperbolic) magnetization. The provided Helmholtz equations allow to deliver and solve a boundary value problem of an elliptic wave guide in case of hyperbolic magnetization with further receiving the dispersing equation.

Keywords: the arbitrary magnetization, tensor of magnetic conductivity of ferrite, cross components of an electromagnetic wave, coefficients of Lame, symbols of Christoffel.

При разработке различных приборов сверхвысокочастотного диапазона (гираторы, циркуляторы, фазовращатели, ослабители и другие) широко применяются намагниченные ферриты [1, 2]. Феррит при этом может быть намагничен продольно, когда направления распространения электромагнитной волны и намагниченности феррита совпадают, или поперечно, когда они перпендикулярны. В большинстве случаев рассматриваются гиротропные волноводы с круглой и прямоугольной формой поперечного сечения 2. В указанных и в других работах анализ гиротроп-ных эллиптических волноводах носит фрагментарный характер или ограничиваются изотропным случаем.

Целью настоящей работы является получение уравнений Гельмгольца НЕ и ЕН волн гиротропного волновода с ортогональной формой поперечного сечения при нормальном намагничивании и на их основе переход к гиротропному эллиптическому волноводу при гиперболическом (нормальном) намагничивании.

1. Уравнения Гельмгольца НЕ-волн

В [4] было получено общее выражение, позволяющие вывести уравнения Гельмгольца НЕ-волны для гиротропного волновода с ортогональной формой поперечного сечения при произвольном намагничивании: