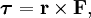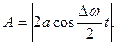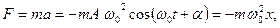Взяв за основу ту же модель, добавим в нее силу вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:
Проводя аналогичные действия, получаем дифференциальное уравнение, описывающее затухающий осциллятор:
Здесь введено обозначение: 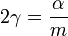
Решение же распадается на три случая.
- При малом трении (γ − γt
- При сильном же трении γ > ω0 решение выглядит следующим образом:
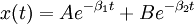
Критическое затухание примечательно тем, что именно при критическом затухании осциллятор быстрее всего стремится в положение равновесия. Если трение меньше критического, он дойдет до положения равновесия быстрее, однако «проскочит» его по инерции, и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.
Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы прочитать его показания можно было максимально быстро.
Затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой Q. По определению, добротность равна:
Чем больше добротность, тем медленнее затухают колебания осциллятора.
У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; со временем он пересечёт положение равновесия неограниченное количество раз. Добротность меньше или равная 0,5 соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.
Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной амплитуда колебаний оказывается примерно в Q раз больше, чем при возбуждении на низкой частоте.
Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в e раз, умноженному на π.
В случае колебательного движения затухание еще характеризуют такими параметрами, как:
- Время жизни колебаний, оно же время затухания, оно же время релаксации. τ — время, за которое амплитуда колебаний уменьшится в e раз.
Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя формально свободные колебания продолжаются бесконечно долго).
- Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону.
. Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.
Коэффициент затухания
величина, характеризующая скорость затухания колебаний
Закон сохранения энергии — основной закон природы, заключающийся в том, что энергия изолированной (замкнутой) системы сохраняется во времени. Другими словами, энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую. Закон сохранения энергии встречается в различных разделах физики и проявляется в сохранении различных видов энергии. Например, в классической механике закон проявляется в ]] закон сохранения энергии называется первым началом термодинамики и говорит
Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то правильнее называть его не законом, а принципом сохранения энергии.
Добро́тность — характеристика колебательной системы, определяющая остроту резонанса и показывающая, во сколько раз запасы энергии в реактивных элементах контура больше, чем потери энергии на активных за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии в течение каждого периода. Колебания в системе с высокой добротностью затухают медленно
Общая формула для добротности любой колебательной системы:
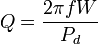
- f — частота колебаний
- W — энергия, запасённая в колебательной системе
- Pd — рассеиваемая мощность.
Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.
Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.
Обратимые процессы дают наибольшую работу. Большую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.
Следует отметить, что термодинамическая обратимость процесса отличается от химической обратимости. Химическая обратимость характеризует направление процесса, а термодинамическая — способ его проведения.
понятие равновесного состояния и обратимого процесса играют большую роль в термодинамике. Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам.
Вынужденные колебания — колебания, происходящие под действием внешней силы, меняющейся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 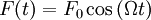
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
теплова́я маши́на
машина (тепловой двигатель, тепловой насос и др.), в которой осуществляется преобразование теплоты в работу или работы в теплоту. В основе действия тепловой машины лежит круговой процесс (цикл термодинамический), совершаемый рабочим телом (газом, водяным паром и др.). Если при осуществлении цикла на одних его участках теплота подводится к рабочему телу, а на других отводится (при более низкой температуре), то рабочее тело совершает работу, равную (для идеальной тепловой машины) разности количеств подведённой и отведённой теплоты.
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадает соответственно с максимальной и минимальной температурами цикла Карно.
КПД тепловой машины Карно
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
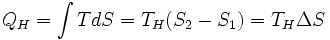
Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику
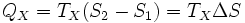
Отсюда коэффициент полезного действия тепловой машины Карно равен
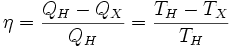
Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Можно показать, что КПД любой тепловой машины, работающей по циклу, отличному от цикла Карно, будет меньше КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где 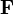
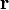
Теплоемкость идеального газа — это отношение тепла, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
Видео:Урок 327. Гармонические колебанияСкачать

Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний
КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА
КОЛЕБАНИЯ
Лекция 1
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний
Колебание – один из самых распространённых процессов в природе и технике. Колебания – это процессы, повторяющиеся во времени. Колеблются высотные здания и высоковольтные провода под действием ветра, маятник заведённых часов и автомобиль на рессорах во время движения, уровень реки в течение года и температура человеческого тела при болезни. Звук – это колебания давления воздуха, радиоволны – периодические изменения напряжённости электрического и магнитного поля, свет – это тоже электромагнитные колебания. Землетрясения – колебания почвы, приливы и отливы – изменение уровней морей и океанов, вызываемые притяжением луны и т.д.
Колебания бывают механические, электромагнитные, химические, термодинамические и др. Несмотря на такое многообразие, все колебания описываются одними и теми же дифференциальными уравнениями.
Первыми учёными, изучавшими колебания, были Галилео Галилей и Христиан Гюйгенс. Галилей установил независимость периода колебаний от амплитуды. Гюйгенс изобрёл часы с маятником.
Любая система, которая, будучи слегка выведена из положения равновесия, совершает устойчивые колебания, называется гармоническим осциллятором. В классической физике такими системами являются математический маятник в пределах малых углов отклонения, груз в пределах малых амплитуд колебаний, электрический контур, состоящий из линейных элементов ёмкости и индуктивности.
Гармонический осциллятор можно считать линейным, если смещение от положения равновесия прямо пропорционально возмущающей силе. Частота колебаний гармонического осциллятора не зависит от амплитуды. Для осциллятора выполняется принцип суперпозиции — если действуют несколько возмущающих сил, то эффект их суммарного действия может быть получен как результат сложения эффектов от действующих сил в отдельности.


где х -смещение колеблющейся величины от положения равновесия, А – амплитуда колебаний, равная величине максимального смещения, 



Время одного полного колебания называется периодом, 


Частота колебаний 


Скорость колеблющейся материальной точки


Таким образом, скорость и ускорение гармонического осциллятора также изменяются по гармоническому закону с амплитудами 






Это дифференциальное уравнение второго порядка называется уравнением гармонического осциллятора. Его решение содержит два постоянные а и 
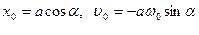
Отсюда 
Если периодически повторяющийся процесс описывается уравнениями, не совпадающими с (1.1.1), он н6азывается ангармоническим. Система, совершающая ангармонические колебания, называется ангармоническим осциллятором.
1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний
В природе очень распространены малые колебания, которые система совершает вблизи своего положения равновесия. Если система, выведенная из положения равновесия, предоставлена себе, то есть на неё не действуют внешние силы, то такая система будет совершать свободные незатухающие колебания. Рассмотрим систему с одной степенью свободы.
Устойчивому равновесию соответствует такое положение системы, в котором её потенциальная энергия 


Будем отсчитывать потенциальную энергию от минимального значения 



где 

С учётом выражения (1.1.4) для силы, действующей на систему, получаем:
Согласно второму закону Ньютона, уравнение движения системы имеет вид: 

Выражений (1.1.5) совпадает с уравнением (1.1.3) свободных гармонических колебаний при условии, что

и имеет два независимых решения: 



где
Из формулы (1.1.6) следует, что частота определяется только собственными свойствами механической системы и не зависит от амплитуды и от начальных условий движения.
Зависимость координаты колеблющейся системы от времени можно определить в виде вещественной части комплексного выражения 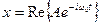
1.1.3. Примеры колебательных движений различной физической природы
Колебания груза на пружине
Рассмотрим колебания груза на пружине, при условии, что пружина не деформирована за пределы упругости. Покажем, что такой груз будет совершать гармонические колебания относительно положения равновесия (рис.1.1.3). Действительно, согласно закону Гука, сжатая или растянутая пружина создаёт гармоническую силу:
где 



Поместим начало отсчета координаты в положение равновесия системы. В этом случае 



Это уравнение совпадает по виду с уравнением движения (1.1.3) системы, совершающей гармонические колебания, его решение будем искать в виде:
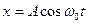
Подставим (1.17) в (1.1.6), имеем: 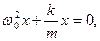
Если в начальный момент времени положение груза было произвольным, то уравнение движения примет вид:

Рассмотрим, как меняется энергия груза, совершающего гармонические колебания в отсутствие внешних сил (рис.1.14). Если в момент времени t=0 грузу сообщить смещение х=А, то его полная энергия станет равной потенциальной энергии деформированной пружины 


В момент времени 

За счёт запаса кинетической энергии груз совершает работу против упругой силы – 

Маятники
Под маятником понимают твёрдое тело, которое совершает под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятники.
Математический маятник – это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной материальной точке.

Отклонение маятника от положения равновесия характеризуется углом φ, который образует нить с вертикалью (рис.1.15). При отклонении маятника от положения равновесия возникает момент внешних сил (силы тяжести) 


Этот момент стремится вернуть маятник в положение равновесия (аналогично квазиупругой силе) и направлен противоположно смещению φ, поэтому в формуле стоит знак «минус».
Уравнение динамики вращательного движения для маятника имеет вид: Iε= 

Будем рассматривать случай малых колебаний, поэтому sin φ ≈φ, обозначим 
имеем: 


Это уравнение гармонических колебаний, его решение:

Частота колебаний математического маятника определяется только его длиной и ускорением силы тяжести, и не зависит от массы маятника. Период равен:

Если колеблющееся тело нельзя представить, как материальную точку, то маятник называют физическим (рис.1.1.6). Уравнение его движения запишем в виде:


В случае малых колебаний 
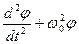

Обозначим 

Математический маятник, который качается с таким же периодом, как и рассматриваемый физический, называется изохронным данному физическому маятнику.

Сложение одинаково направленных колебаний можно производить методом векторных диаграмм. Любое гармоническое колебание можно представить в виде вектора следующим образом. Выберем ось х с началом отсчета в точке О (рис.1.1.7)
Из точки О построим вектор 



то есть она совершает гармонические колебания с амплитудой а.





результирующий вектор 


Проведем сложение взаимно перпендикулярных колебаний. Пусть материальная точка совершает два взаимно перпендикулярных колебания частотой 



Сама материальная точка при этом будет двигаться по некоторой криволинейной траектории.
Из уравнения движения следует: 
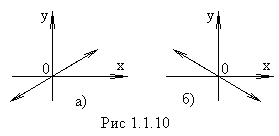

Из уравнения (1.1.9) можно получить уравнение эллипса (рис.1.1.9):
Рассмотрим частные случаи этого уравнения:






2. Если разность фаз 



3. Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112).
Рассмотрим сложение колебаний одного направления, частоты которых мало отличаются друг от друга. В этом случае результирующее движение можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.
Пусть частота одного колебания 

Сложим эти выражения:





Частота изменения амплитуды – частота биений – равна разности частот складываемых колебаний 
Энергия колебаний
Смещение колеблющейся точки от положения равновесия, описывается уравнением:


— то есть сила пропорциональна смещению х и направлена против смещения к положению равновесия. Эта сила называется возвращающей силой. В случае груза на пружине возвращающей силой является сила упругости, в случае математического маятника – составляющая силы тяжести.
Возвращающая сила по характеру подчиняется закону Гука F= -kx, где
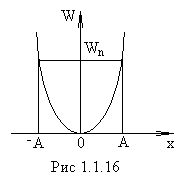
– коэффициент возвращающей силы. Тогда потенциальная энергия колеблющейся точки равна:
(постоянную интегрирования выбирают равной нулю, чтобы при х=0 энергия Wn=0).
где 



Таким образом, полная механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия (х=0) потенциальная энергия переходит в кинетическую:
В промежуточных точках полная энергия равна
а скорость


Средние за период значения кинетической и потенциальной энергии одинаковы и равны 

АНГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Видео:Гармонический осциллятор. Груз на пружине. 3 метода решения.Скачать

Обыкновенные дифференциальные уравнения
Дифференциальные уравнения – это язык физики
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дифференциальные уравнения второго порядка
ДУ второго порядка часто встречаются в физике: закон Ньютона, уравнение Шредингера, диффузия.
- restart:
- E2:=diff(y(t),t$2)=-g;
- S2:=dsolve(,y(t));
Это очевидный результат.
Заметьте несколько деталей.
Для ввода начальных условий для производной от y применена D(y) , что означает dy/dt ( D – это общий символ производной для Maple), затем добавили (0) , чтобы сказать, что производная вычислена при t=0 . Это означает, что diff и D – это производные, но между ними есть тонкое различие, которое надо понимать. Оно обсуждено в разделе о производных (см. D и diff ). Поэтому или запоминайте синтаксис команды dsolve (выше), или запомните, где его легко найти. Кроме того, учтите, что применяемая в пакете Physics команда diff может давать другой результат – см. описание команд пакета Physics.
Это второе знаменитое ДУ второго порядка.
Maple решает его в общем виде с произвольными константами:
Предупреждение: эта форма решения опасна, поскольку нет гарантии, что при каждом запуске рабочего листа с командой dsolve в таком виде получим на выходе _C1 с синусом и _C2 с косинусом. В Maple есть собственная логика такого выбора, которая даже для более простых ДУ кажется случайной. Поэтому не давайте Maple выбирать, делайте это сами. Для этого скопируйте решение мышкой в новую строку и выберите неизвестные коэффициенты, например избавьтесь от неудобного y(t)= , заменив его естественным присвоением:
Теперь каждый раз расчет величин A и B будет срабатывать одинаково, потому что «насильственно» установлено, что A – с синусом, а B – с косинусом.
Если константы определяются начальными условиями, есть форма команды dsolve , которая будет определять их автоматически. Например, нужно решить ДУ E3 с начальными условиями y(0) = 1 и dy/dt(0) = 2. Тогда пишем:
Применим assign , чтобы Maple дал выражение для y(t) :
Теперь построим график решения:
Не работает. Рамка есть, но нет функции. И нет догадок, что не так. Для отладки надо бы подставить несколько значений t в y(t) . Но вспомним, что y(t) выглядит как выражение, но не совсем им является, и что подстановка значений для t запустит его. Рассмотрим y(t) с этой точки зрения и прикинем, можно ли увидеть, что не так:
Команда plot даст численные значения t , но ведь 

OК, теперь сделаем так:
Решение этой задачи было достаточно легким. Но так же легко Maple решает и более сложные задачи.
Усложним условия и рассмотрим
Поставим в гармонический осциллятор затухание (демпфер), для чего добавим силу затухания в виде 
и мы получаем общее решение:
Где же тогда появятся синусы и косинусы? Проблема в том, что Maple не знает, насколько велики 


OK, Maple согласен с интуицией.
Теперь изменим затухание и представим, что произойдет, если нагреть масло или использовать вместо него WD-40 (жидкая смазка) или, может быть, воздух. Маятник начнет колебаться с малым затуханием. Например, если τ = 20, то Maple дает:
Теперь он колеблется дольше и медленно затухает. Но какое чудо в решении превратило экспоненту в синусы и косинусы? Вспомним формулу Эйлера: 
т. е. в экспоненте константы стали комплексными, поэтому решение перешло от распада к колебаниям.
Это поднимает вопрос о величине τ, при которой происходит переход от чистого затухания к затухающим колебаниям. Посмотрите на общий вид решения и увидите, что в экспонентах есть квадратный корень 

Пусть Maple решит задачу о гармоническом осцилляторе с затуханием для случая критического затухания при 
Примените Maple, чтобы получить общие решения ДУ второго порядка:
(a) 
(b) 
(c) 
🎦 Видео
Консультация к устному экзамену. Механика. Часть 6: "Колебания"Скачать

Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

70. Затухающие колебанияСкачать

Урок 343. Затухающие колебания (часть 1)Скачать

Микролекция: Гармонический осцилляторСкачать

Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

71. Вынужденные колебанияСкачать

Билеты №43,44 "Параметры колебательных контуров"Скачать

основы теорий колебаний и волн. Задачи.Скачать

Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Затухающие колебанияСкачать

Классические уравнения | квантовый гармонический осциллятор | 1Скачать

Лекция №11 "Колебания" (Булыгин В.С.)Скачать

Затухающие колебанияСкачать

Затухающие колебанияСкачать

Урок 344. Затухающие колебания (часть 2)Скачать

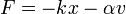
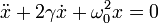
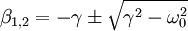
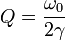
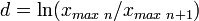 . Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.
. Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.