Уравнение затухающих колебаний через синус

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r — коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

Если затухания выражены слабо (β→0), то . Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А₀ и φ₀ — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

τ — время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D :

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынуж­денных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механи­ческой системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.

Затухающие колебания в контуре и их уравнение

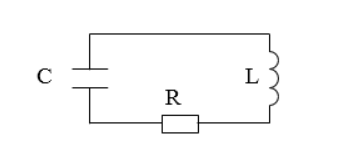
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.

Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

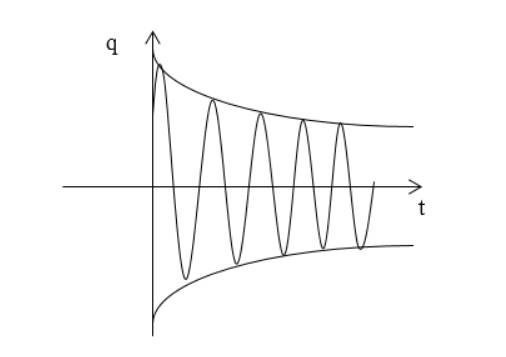
Функция изображается аналогично рисунку 2 .

Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

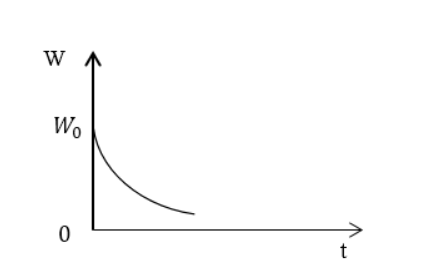
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.

Решение

Если колебания в контуре затухают медленно, то:

Очевидно, выражение энергии, запасенной в контуре, вычислим из

W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .

Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.

Затухающие колебания

Определение затухающих колебаний

Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.

Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.

Уравнение колебаний пружинного маятника с затуханием

Иногда, если тело движется в веществе, силу сопротивления ($<overline>_

$), которая действует на рассматриваемое тело, при маленьких скоростях его движения, считают прямо пропорциональной скорости ($overline$):

[<overline>_

=-beta overlineleft(1right),]

где $beta $ — коэффициент сопротивления.

Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:

где $dot=v_x.$ Принимая во внимание равенства:

(где $_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $gamma $=0) той же колебательной системы; $gamma $ — коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:

Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания . ) описывают при помощи уравнения формы (4).

Уравнение затухающих колебаний имеет точное решение:

где $omega =sqrt<^2_0-^2>$; $A_0$ — начальная амплитуда колебаний, задаваемая начальными условиями; $varphi $ — постоянная из начальных условий. При $gamma ll _0$, $omega approx _0$, параметр $A_0e^$ можно считать медленно изменяющейся во времени амплитудой колебаний.

Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.

Диссипация энергии при затухающих колебаниях

Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.

Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:

[frac

=-fracleftlangle E_krightrangle left(6right),]

где $frac

$ — скорость изменения энергии колебаний; $leftlangle E_krightrangle $ — средняя величина кинетической энергии за период колебаний. Уравнение (6) не применяют для промежутков времени, которые меньше периода колебаний.

Так как мы считаем затухание малым, то $leftlangle E_krightrangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:

[leftlangle E_krightrangle =fracleft(7right).]

В таком случае уравнение (6) можно записать в виде:

Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:

где $E_0$ — величина энергии колебательной системы в начальный момент времени.

Так как энергия колебаний пропорциональна квадрату амплитуды ($Esim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:

$A_0$ — начальная амплитуда колебаний.

Видео:ЧК_МИФ РЕШЕНИЕ УРАВНЕНИЯ ДЛЯ ЗАТУХАЮЩИХ КОЛЕБАНИЙ В СЛУЧАЕ МАЛЫХ ЭНЕРГЕТИЧЕСКИХ ПОТЕРЬСкачать

Время жизни колебаний. Период затухающих колебаний. Декремент затухания

Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $tau =frac$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($tau gg T$). За время жизни происходит много колебательных движений.

Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.

Период затухающих колебаний считают равным:

Пусть $Aleft(tright) и A(t+T)$ — амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:

называют декрементом затухания. Натуральный логарифм декремента затухания ($theta $):

называют логарифмическим декрементом затухания. Для колебательной системы $theta $ постоянная величина.

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Примеры задач с решением

Задание. Каков коэффициент затухания маятника ($gamma $), если за $Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?

Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:

По условию задачи имеем:

С другой стороны:

где $t_2-t_1=Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:

Выразим $gamma $ из (1.3) учтем, что $frac=n$:

Ответ. $gamma =frac<>$

Задание. Что представляет собой фазовая траектория затухающего колебания?

Решение. Фазовой траекторией называют траекторию движения в плоскости $left(x;;vright).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $left(x,vright),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:

Фазовая траектория затухающего колебания, если

[<overline>_

=-beta overlineleft(2.2right),]

представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.

🌟 Видео

Затухающие колебания. Вынужденные колебания. Физика 11 классСкачать

Затухающие колебания на экране осциллографа.Скачать

5.4 Уравнение гармонических колебанийСкачать

Затухающие колебания, Киевнаучфильм, 1978Скачать

Урок 327. Гармонические колебанияСкачать

Честный вывод уравнения колебанийСкачать

Затухающие колебания Лекция 11-1Скачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

71. Вынужденные колебанияСкачать

Якута А. А. - Механика - Гармонические колебания. Собственные затухающие колебанияСкачать

Урок 344. Затухающие колебания (часть 2)Скачать