- Ваш ответ
- решение вопроса
- Похожие вопросы
- При гармонических колебаниях вдоль оси OX координаты тела изменяются по закону x = 0, 9sin ( 3t ) м?
- Напишете закон гармонических колебаний тела, если амплитуда колебаний его = 2м а период 4 с?
- Зная, что тело совершает гармонические колебания по закону х = 0, 05 cos(π / 6 * t + π / 6)?
- При гармонических колебаниях вдоль оси ох координата тела изменяется по закону х = 0, 02cos20 пt ( м)?
- При гармонических колебаниях вдоль оси Ох координата тела изменяется по закону х = 0, 9sin 3t (м)?
- Тело совершает гармоническое колебание по закону x = 20sinПt?
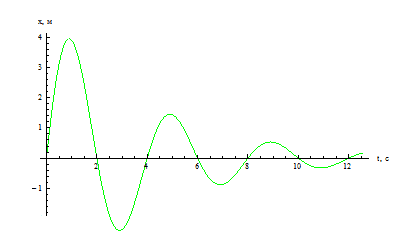
- Как по графику гармонических колебаний определить амплитуду, период и частоту колебаний тела?
- Тело совершает гармонические колебания по закону х = 0, 2sin (4πt) Определите частоту колебаний?
- СРОЧНО?
- ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО1)какая сила приводит к тому?
- Период колебаний тела 10 — 2 с?
- Гармонические колебания
- теория по физике 🧲 колебания и волны
- Уравнение движения гармонических колебаний
- Период и частота гармонических колебаний
- Зависимость частоты и периода свободных колебаний от свойств системы
- Фаза колебаний
- Превращение энергии при гармонических колебаниях
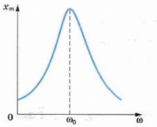
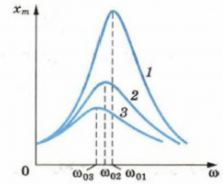
- Резонанс
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Ваш ответ
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

решение вопроса
Видео:Урок 327. Гармонические колебанияСкачать

Похожие вопросы
- Все категории
- экономические 43,415
- гуманитарные 33,633
- юридические 17,906
- школьный раздел 608,066
- разное 16,856
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:10 класс, 19 урок, График гармонического колебанияСкачать

При гармонических колебаниях вдоль оси OX координаты тела изменяются по закону x = 0, 9sin ( 3t ) м?
Физика | 5 — 9 классы
При гармонических колебаниях вдоль оси OX координаты тела изменяются по закону x = 0, 9sin ( 3t ) м.
Чему равна частота колебаний тела?
Асельдер Абдулкеримов Нижний Новгород.
Циклическая частотаω = 3 с⁻¹
частотаν = ω / 2π, ν = 3 / 2π = 0, 48 Гц.
Видео:Выполнялка 53.Гармонические колебания.Скачать

Напишете закон гармонических колебаний тела, если амплитуда колебаний его = 2м а период 4 с?
Напишете закон гармонических колебаний тела, если амплитуда колебаний его = 2м а период 4 с.
Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Зная, что тело совершает гармонические колебания по закону х = 0, 05 cos(π / 6 * t + π / 6)?
Зная, что тело совершает гармонические колебания по закону х = 0, 05 cos(π / 6 * t + π / 6).
А) Определите амплитуду, циклическую частоту и начальную фазу колебаний тела.
Б) Вычислите период и частоту колебаний тела.
В) Найдите фазу колебаний и координату тела через 1 с после начала отсчета времени.
Видео:Урок 329. Задачи на гармонические колебания - 1Скачать

При гармонических колебаниях вдоль оси ох координата тела изменяется по закону х = 0, 02cos20 пt ( м)?
При гармонических колебаниях вдоль оси ох координата тела изменяется по закону х = 0, 02cos20 пt ( м).
Чему равна частота колебаний ускорения тела?
Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

При гармонических колебаниях вдоль оси Ох координата тела изменяется по закону х = 0, 9sin 3t (м)?
При гармонических колебаниях вдоль оси Ох координата тела изменяется по закону х = 0, 9sin 3t (м).
Чему равна амплитуда колебаний ускорения?
А)0, 1 м / с2 В)0, 9м / с2 Б)0, 3 м / с2 Г)2, 7м / с2 Д)8, 1м / с2.
Видео:5.4 Уравнение гармонических колебанийСкачать

Тело совершает гармоническое колебание по закону x = 20sinПt?
Тело совершает гармоническое колебание по закону x = 20sinПt.
Определите амплитуду, период колебаний и частоту.
Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Как по графику гармонических колебаний определить амплитуду, период и частоту колебаний тела?
Как по графику гармонических колебаний определить амплитуду, период и частоту колебаний тела?
Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Тело совершает гармонические колебания по закону х = 0, 2sin (4πt) Определите частоту колебаний?
Тело совершает гармонические колебания по закону х = 0, 2sin (4πt) Определите частоту колебаний.
Видео:Урок 335. Анализ графика гармонических колебанийСкачать

СРОЧНО?
Координата колеблющегося тела изменяется по закону х = cos2Пt 3.
Чему равна амплитуда, циклическая частота, собственная частота, и период колебаний, если в формуле все величины выражены в единицах СИ?
Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО1)какая сила приводит к тому?
ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО
1)какая сила приводит к тому.
Что колебания груза на пружине постепенно прекращаются?
2)девочка, качающаяся на качелях, проходит положения равновесия 30 раз в минуту.
Определите частоту колебания качелей с девочкой
3)при гармонческих колебаниях вдоль оси ОХ координата тела изменяется по закону x = 0.
Чему равна циклическоя частота колебаний тела?
Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Период колебаний тела 10 — 2 с?
Период колебаний тела 10 — 2 с.
Чему равна частота колебаний?
На этой странице вы найдете ответ на вопрос При гармонических колебаниях вдоль оси OX координаты тела изменяются по закону x = 0, 9sin ( 3t ) м?. Вопрос соответствует категории Физика и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.
Чтоб вычислить цену деления , надо взять 2 ближайшие прономерованные точки , и от большего из них отнят меньшее , и разделить на число разделенных частей между этими ближайшими точками. И так , (24 — 0) : 8 = 3 , и получим ответ 3.
1 : сначала нагреваем лед. По формуле стандартной Q1 = cm(t2 — t1). T2 = 0, t1 = — 20. Дальше плавим по формуле Q2 = qm. Дальше нагреваем до температуры кипения. Q3 = cm(t3 — t2), t3 = 100. Испаряем) Q4 = (лямбда) m. Q = Q1 + Q2 + Q3 + Q4 2 : ..
Vo = 36 / 3. 6 = 10 м / с v = 0 t = 10 c a = ? = = = a = (v — vo) / t = (0 — 10) / 10 = — 1 м / с² = = = = = = = = = = = = = = = = = = = = = = = = =.
Тепловое равновесие — состояние термодинамической систем, в которое она самопроизвольно переходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды.
2ч + 3ч = 5ч 100км + 80км = 180км 180км / 5ч = 36 км.
1. найти температуру плавления металла, который дан, подставь в формулу и посчитай 2. Сравни два металла = если температура плавления больше , чем 950, то они находятся в жидком состоянии Если меньше 950 , то в твердом 3. 10 тонн = 10000 кг Q = лям..
Скоріш за все для риби тому шо вона менша.
А можешь на русском написать.
M — масса V — объём n — мощность t — время e — энергия.
X₀ = 0м x₁ = 400м x₂ = 0м S = l начальная координата — конечная | S = | x₀ — x2 | S = | 0 — 0 | = 0м (перемещение) S = ( | Конечная точка — начальная | ) * 2 (умножаем на 2, т. К. он прошел это расстояние два раза) S = (400 — 0) * 2 = 800м (путь).
Видео:Физика 9 класс Уравнение и график гармонических колебаний Пример решения задачиСкачать

Гармонические колебания
теория по физике 🧲 колебания и волны
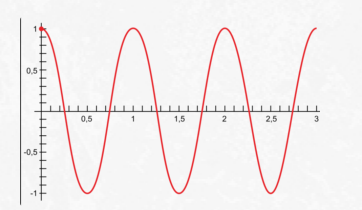
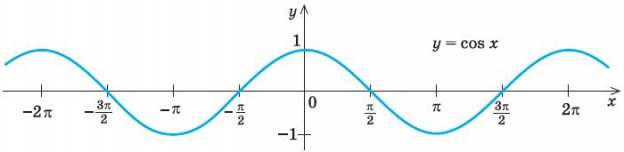
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Уравнение движения гармонических колебаний
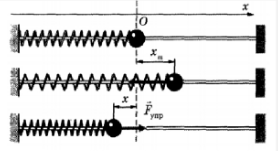
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x″ = − x m a x cos . t = − x
Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x = x m a x cos . √ k m . . t
Тогда первая производная примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x′ = − √ k m . . x m a x sin . √ k m . . t
Вторая производная примет вид:
x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x = x m a x sin . √ k m . . t
x = x m a x cos . √ k m . . t
Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω0:
x = x m a x sin . ω 0 t
x = x m a x cos . ω 0 t
Само уравнение движения, описывающего свободные колебания, примет вид:
Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω 0 = 2 π T . . = 2 π ν
Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Видео:КОЛЕБАНИЯ физика 9 класс решение задачСкачать

Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω 0 = √ k m . . = 2 π T . . = 2 π ν
Отсюда период и частота колебаний соответственно равны:
T = 2 π ω 0 . . = 2 π √ m k . .
ν = 1 2 π . . √ k m . .
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:
Отсюда период и частота колебаний математического маятника соответственно равны:
T = 2 π ω 0 . . = 2 π √ l g . .
ν = 1 2 π . . √ g l . .
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
Искомое число колебаний равно отношению времени к периоду колебаний:
Период колебаний для математического маятника определяется формулой:
N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68
Видео:Гармонические колебанияСкачать

Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:
ϕ = ω 0 t = 2 π t T . .
t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 |
| Фаза, ϕ (рад) | 0 |