Математическая модель, описывающая процессы, подобные развитию эпидемии называется уравнением Ферхюльста, или логистическим уравнением. Уравнение описывает увеличение некоторой популяции в присутствии ограничения ее максимума. Популяция (например, количество заболевших) в начале эпидемии увеличивается экспоненциально, но количество заболевших ограничено численностью населения и постепенно рост замедляется. Кривая, иллюстрирующая этот процесс называется логистической.
К сожалению, статистические данные о заболеваемости и смертности неоднородны и не всегда достоверны. Это связано с разным развитием медицины по странам и отсутствием общих стандартов в том, кто является заболевшим и, даже, причины смерти. Например, в Италии, если скончался зараженный человек, то в статистике определяется смерть от коронавируса. А в Германии (и в России) чаще диагностируют смерть от обострившегося хронического заболевания. Поэтому в Италии смертность (4032/47021) = 8.6%, а в Германии всего (45/18323) = 0.25% от количества заболевших. В каких-то странах проводят массовое тестирование жителей и включают в статистику даже бессимптомных вирусоносителей, в других странах диагностируют только тяжелых больных, да и то не всегда.
Графики официальной статистики по странам можно изучить на сайтах https://observablehq.com/@elaval/coronavirus-worldwide-evolution
http://shinyapps.org/apps/corona/
Хорошую статистику дает паром Diamond Princess.
3500 человек на борту (большинство — пенсионеры).
712 заразившихся, из них 362 бессимптомно.
7 смертных случаев.
Почему 80% не заразилось, неизвестно. Возможно, некоторые люди этой инфекцией совсем не заражаются, но это не точно…
Из выступления Генерального директора ВОЗ от 17.02.2020.
«У более 80% пациентов болезнь протекает в легкой форме и заканчивается полным выздоровлением.
Примерно в 14% случаев течение болезни тяжелое и сопровождается, в частности, пневмонией и одышкой.
И, наконец, у порядка 5% пациентов развивается опасное для жизни заболевание, сопровождающееся такими проявлениями, как респираторная недостаточность, септический шок и полиорганная недостаточность.
В 2% случаев заражение вирусом приводит к смерти, причем этот риск возрастает пропорционально возрасту пациента. „
Возможно, что Гендиректор ВОЗ совсем не учел бессимптомных инфицированных, поэтому делим все пополам.
Итак, на 100% инфицированных:
90% бессимптомно, или в легкой форме;
10% — требуется госпитализация, из них:
2.5% — тяжелые, требуется реанимация (наверное, искусственная вентиляция легких?);
1% — смертность.
Точное решение логистического уравнения:
N=M*EXP(r*t)/(1+EXP(r*t)); где
N — размер популяции в момент t;
M — максимальный размер популяции;
r — скорость роста популяции, увеличение за день (проценты/100);
t — текущее время в днях, отсчитывается от середины логистической кривой.
Для определения времени:
t=(1/r)*LN(N/(M-N));
Простота использования логистического уравнения заключается в том, что для его решения нужно всего 2 параметра — максимальный размер популяции и скорость ее роста.
Для примера посчитаем смертность в Италии. Население Италии — 60 млн. человек. Будем считать, что вирусом заразятся половина населения, 30 млн. Увы, 1%, 300 тыс. из них могут погибнуть. В настоящее время умерло 4032 человека, скорость роста процесса — 15% в день. Число заболевших в Италии в начале эпидемии увеличивалось на 25% в день, сейчас, при карантине, 13%. Смертность отстает от количества заболевших, умирают через 11 дней после заражения, так что считаем, что и смертность упадет до 13%.
r=0.13; N=4032; M=300000.
Ответ пугает. t=33. Через 33 дня в Италии могут умереть от вируса 150 тысяч человек. В это время будут умирать до 9700 человек в день.
Если бы карантина не было, скорость распространения осталась бы 25%, максимум был бы достигнут на 17 день, ежедневная смертность в максимуме — 18650 человек. Карантин сдвигает процесс и уменьшает максимум. Справится ли итальянская медицина?
Но вместо закрытия промышленности, вместо полного карантина есть более элегантное решение.
По данным Высшего института здоровья Италии почти 90% умерших в Италии старше 70 лет. 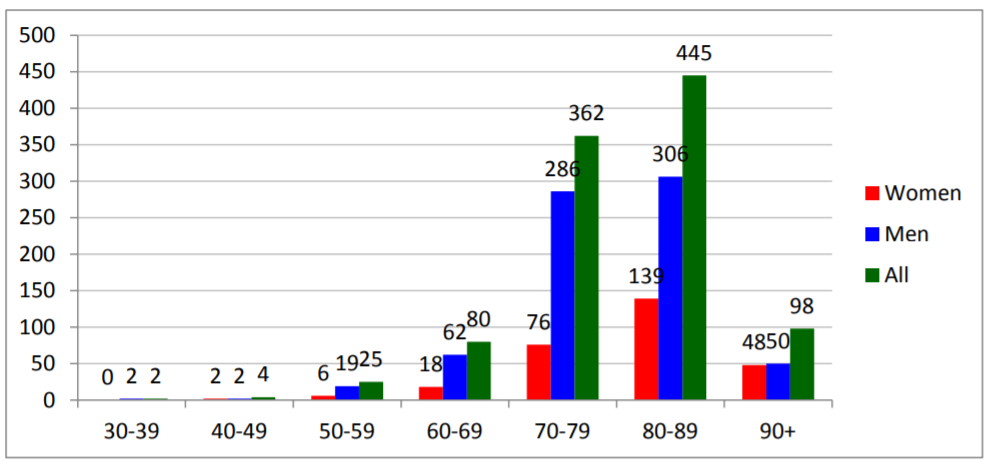
При r=0.2; M=30000, максимум будет достигнут через 28 дней. Максимальное количество новых смертей в день — 1495. 
Если также изолировать и более молодых с опасными заболеваниями, количество смертей можно еще уменьшить. Наиболее распространенные хронические патологии у умерших:
ишемическая кардиопатия — 37,3%
мерцательная аритмия — 26.5%
перенесенный инсульт — 8,2%
артериальная гипертензия — 76,5%
сахарный диабет — 37,3%
деменция — 4,5%
хроническая обструктивная болезнь легких — 9,7%
рак, активный в течение последних 5 лет — 19,4%
хроническая гепатопатия — 7%
хроническая почечная недостаточность — 17,5%
Количество заболевших коронавирусом в России увеличивается более чем на 25% ежедневно. Это означает в 10 раз за 10 дней, в 1000 раз за месяц. С такими темпами через месяц у нас будут сотни тысяч больных. Самые строгие карантинные мероприятия смогут снизить темпы ежедневного роста заболеваемости вдвое, до 13% (на примере Италии). Карантинные меры обрушивают экономику и не достигают поставленной задачи — снизить нагрузку на медицину до приемлемого уровня.
Между тем, имеется эффективное решение проблемы.
90% тяжелых больных и смертельных исходов наблюдается у лиц, старше 70 лет. Строгий карантин для пожилых людей и хронических больных. Для этого надо задействовать пансионаты и дома отдыха. Установить строгий режим, персонал не должен быть местным и также не должен покидать карантин. Карантины должны охраняться Росгвардией. Первые две недели карантины должны быть индивидуальными.
Для остальных жителей России карантин может быть снят, или ослаблен.
Таблица прогноза сроков и максимального количества тяжелых больных.
| Дней до максимума эпидемии | Максимально тяжелых случаев за этот день | |
| Существующее положение | 39 | 108800 |
| Карантин | 65 | 65500 |
| Изоляция пожилых без общего карантина | 37 | 8700 |

Времени нет. Если оставить все как есть, к началу мая мы будем иметь сотни тысяч только тяжелых больных, нуждающихся в реанимации.Ежедневно будет поступать 100000 новых. Общий карантин растянет эти сроки вдвое и вдвое снизит приток больных.
Изоляция группы риска снизит количество тяжелых больных и смертей в 10 раз.
Хотелось бы донести эту информацию до властей.
- Модели роста популяций: модель Ферхюльста (логистический рост), модель с наименьшей критической численностью.
- Дифференциальные модели в экономике, биологии и медицине
- п.1. Экономика. Равновесная цена в модели Вальраса
- п.2. Биология. Логистическое уравнение Ферхюльста для роста популяции
- п.3. Медицина. Модель развития эпидемии SIR
- 📹 Видео
Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать
![Уравнение, которое меняет взгляд на мир [Veritasium]](https://i.ytimg.com/vi/DH1cv0Rdf2w/0.jpg)
Модели роста популяций: модель Ферхюльста (логистический рост), модель с наименьшей критической численностью.
- Геннадий Букреев 4 лет назад Просмотров:
1 СЕМИНАР Модели роста популяций: модель Ферхюльста (логистический рост), модель с наименьшей критической численностью. ЛОГИСТИЧЕСКИЙ РОСТ (УРАВНЕНИЕ ФЕРХЮЛЬСТА) Частым явлением в природе является ограниченность ресурсов (пищевых, территориальных) и, как следствие, внутривидовая конкуренция. Как правило, если численность популяции очень мала, то конкуренция не влияет на удельную скорость роста популяции r. Когда же численность возрастает и приближается к некоторому предельному значению, удельная скорость роста падает до нуля. Предельное значение называется емкостью экологической ниши популяции. Величина К соответствует такой численности популяции, при которой фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может только восстанавливать в каждом поколении свою численность. В этот момент количество родившихся особей уравновешивается количеством погибших. Предположим, что зависимость удельной скорости роста популяции от ее численности линейна (рис. ). Получим уравнение dx() r = r x() (.) d x или dx() r = x() r x(). (. * ) d
2 Семинар. Модели роста популяций Рис. Простейшая линейная зависимость, иллюстрирующая снижение удельной скорости роста в связи с увеличением плотности популяции. Уравнение (. * ) получило название «уравнение логистического роста» или «уравнение Ферхюльста». Слагаемые в правой части уравнения (. * ) можно интерпретировать следующим образом. Удельная (средняя) скорость рождаемости есть некоторая положительная постоянная, не зависящая от времени и размера популяции x() (положительное слагаемое r). А удельная (средняя) смертность пропорциональна размеру популяции (отрицательное слагаемое x() r ). Увеличение смертности с ростом популяции может происходить благодаря эффектам скученности или усиливающейся конкуренции за доступные пищевые ресурсы. dx r Раскроем скобки в уравнении (. * ): = x r x. d Первое слагаемое будет нам давать информацию о неограниченном росте популяции. Второе о влиянии внутривидовой конкуренции (отрицательном влиянии взаи-
3 Учебное пособие «Математические модели в биологии» r модействия двух особей одного вида: x ) на скорость роста популяции. Исследуем уравнение логистического роста (уравнение Ферхюльста,. * ). Сначала находим стационарные значения численности популяции: r r x r x = x = или r x =. Получаем два стационарных значения x = и, x =. Будут ли эти стационарные состояния устойчивыми? Воспользуемся аналитическим методом Ляпунова. Согласно ему для определения устойчивости необходимо определить знак производной функции f ( x ), стоящей в правой части дифференциального уравнения, в точках x (подробный вывод см. в разделе Семинар ). Производная функция равна: r = = r f ( x) x r x r x Подставляем стационарные значения: r f ( x ) = r x = r. Показатель удельной скорости x= x = роста r есть положительная константа ( r > ), что означает неустойчивость стационарного состояния x =. Производная функции в точке x :. r f ( x) = r x = r. x= x = Величина r отрицательная, т.е. стационарное состояние x = является устойчивым.
4 Семинар. Модели роста популяций По какому закону будет изменяться во времени численность популяции x()? Для ответа на этот вопрос решим дифференциальное уравнение (.) методом разделения переменных. dx rd x ( x ) = (для сокращения записи вместо x() будем писать x, подразумевая, что численность x есть функция от времени); + dx = r d ; x ( x) ( ln ln( )) x x = r+ C (численность x есть положительная величина, поэтому при интегрировании знак модуля в выражении ln( x ) опускаем, C произвольная ‘ константа); x ln = r + C ; x x x x x = Ce r = Ce, C = e r. C ; Пусть в начальный момент времени численность равнялась x() = x. Определим величину константы C: x x = C. Получим окончательную формулу зависимости численности популяции от времени: x () x = x() x e r или r xe x () =. (.) r x + x e 3
5 Учебное пособие «Математические модели в биологии» Знак модуля можно опустить, поскольку величины x и x() всегда одного знака (см. дальнейшее исследование). Построим график полученной зависимости (.) в области положительных значений времени. В начальный момент времени имеем x() = x. При + численность популяции стремится к величине емкости экологической ниши: x e x x = = = = r lim x( ) lim lim + + r x x + xe + + x x r e x (так как lim = ). + r e На графике существование этого предела отражается в наличии горизонтальной асимптоты x() =. r Знаменатель функции x() равен x + xe. Если r начальное значение x , знаменатель в ноль не обращается. При x > знаменатель обращается в ноль, когда as = ln. Аргумент лога- x r x рифма x x данном случае меньше, поэтому значение as меньше нуля. Таким образом, в случае x > в области отрицательных значений будет иметь место вертикальная асимптота as = ln x r x. 4
6 Семинар. Модели роста популяций Теперь исследуем первую и вторую производную функции (.), чтобы определить, есть ли у кривой, задаваемой этой функцией, экстремумы или перегибы: x () ( ) r ( x + xe ) ( ) r ( ) rxe x + xe xe rxe r r r r r xe = r = = x + x e x + x e rx e x = r. Производная x () > в случае x производная x () функция x() монотонно убывает и асимптотически стремится к величине. r rxe ( x ) x () = = r ( x+ xe ) ( ) ( ) ( ) ( ) ( ) r r r r r xe x x + xe rxe x x + xe = = r ( x + x e ) r ( )( + ) r 4 ( ) r ( x + x e ) r r x e x x x e r = x + xe xe = ( ) = r rxe x 3 r ( x + xe ) r ( x xe ). 4 5
7 Учебное пособие «Математические модели в биологии» В случае x > вторая производная в ноль не обращается, функция x() перегибов не имеет. Рассмотрим случай x , т.е. x , то p 8 Семинар. Модели роста популяций растать, пока численность не достигнет значения, а затем начнет снижаться, стремясь к нулю. Если начальная численность популяции составляет более половины емкости экологической ниши, то размер популяции будет увеличиваться, стремясь к значению, а скорость ее роста будет неуклонно снижаться. Изменение характера развития популяции (переход от возрастания скорости роста к снижению в точке x () = ) про- изошло до того, как исследователь начал за ней наблюдать (т.е. до момента времени = ). Если же размер популяции в начальный момент времени больше предельно возможного значения, то численность популяции будет снижаться (рис..). x() x x x p p Рис. График решения логистического уравнения. 7
9 Учебное пособие «Математические модели в биологии» МОДЕЛЬ ПОПУЛЯЦИИ С НАИМЕНЬШЕЙ КРИТИЧЕСКОЙ ЧИСЛЕННОСТЬЮ В рассмотренной модели прирост численности популяции представлен линейным членом rx(). Строго говоря, это применимо лишь к тем видам, размножение которых происходит путем деления или самооплодотворения. Если же размножение предполагает скрещивание разнополых особей, то прирост будет тем выше, чем больше количество встреч между особями. Тогда для разнополой популяции прирост численности должен выражаться квадратичным членом rx (). При большой численности в популяции лимитирующим фактором становится количество половозрелых самок в популяции. Кроме того, важно учесть время, в течение которого может состояться оплодотворение. Если это время больше времени, в течение которого особь способна к размножению, то популяция вымирает. Уравнение, учитывающее фактор разнополости и количество самок, готовых к оплодотворению, имеет вид dx() β[ x()] = α. Учитывая смертность, пропорциональd β + τ x() cp Пусть Т среднее время между двумя последующими оплодотворениями, τ среднее время вынашивания плода, постоянное для каждого вида, cp среднее время, в течение которого может состояться оплодотворение: cp = T τ. Вероятность встречи, ведущей к оплодотворению, тем больше, чем больше соотношение cp T. Тогда коэффициент размножения для разнополых популяций r, можно представить в виде: cp cp r = α = α T + τ, где α коэффициент пропорциональности; cp величина, уменьшающаяся при возрастании плотности популяции: β = cons. Тогда, dx() cp x() x β β = α = α x = α x d + τ β x() + τ β + τx() cp cp β =, x() [ ( )] [ ( )] [ ( )]. 8
10 Семинар. Модели роста популяций ную численности популяции с коэффициентом γ, получаем уравнение: dx() [ x()] x() d = β α γ β + τx(). (.3) Уравнение (.3) имеет два стационарных значения: x = и x = γβ L αβ γτ = (значения параметров модели задаются такими, чтобы величина L была положительной). Исследуем устойчивость стационарных состояний графическим методом. Для этого необходимо определить знак β x x функции f( x) = α γx= (( αβ γτ) x γβ). Знаменатель функции положителен при положительных значе- β + τx β + τx ниях x, меняет знак при прохождении через значение β x =. Числитель меняет знак при прохождении через τ стационарные точки x,. В результате имеем f( x ) > при dx x > x = L, в области 11 Учебное пособие «Математические модели в биологии» численность (плотность). Она индивидуальна для каждого вида. График зависимости численности популяции, описываемой моделью (.3) от времени представлен на рис..3 б. fx ( )= dx d а x() б L x = x =L x Рис..3. Модель популяции с наименьшей критической численностью. Зависимость скорости роста популяции от ее размера (а) и динамика численности популяции (б). Учтем в модели (.3) важный фактор внутривидовой конкуренции. В этом случае получим общий закон, описывающий динамику разнополой популяции в условии ограничения ресурсов: dx() [ x()] x x d = β α γ δ β + τx() () [ ()]. Уравнение имеет три стационарных значения: (.4) βx x = α γx δx = ( αβx γ( β+ τx) δx( β+ τx) ) = β+ τx β+ τx x = ( δτ x + x( αβ γτ βδ ) γβ ). β+ τx Это нулевое решение x =, а также два значения, обращающих в ноль квадратный трехчлен: x ˆ = L и x ˆ 3 =. Значения численности ˆL и ˆ являются критическими: 3
12 Семинар. Модели роста популяций x ˆ = L минимально возможная численность, x ˆ 3 = максимально возможная (параметры модели α, β, τ, γ, δ выбирают такими, чтобы величины ˆL и ˆ были положительными). Устойчивость стационарных состояний проверим, аналогично предыдущему случаю, графическим dx x методом. Функция f ( x) = ( x Lˆ)( x ˆ) d = β + τx модели (.4) в положительной области значений переменной x меняет знак с «плюса» на «минус» при переходе через x = (это стационарное значение устойчиво), затем с «минуса» на «плюс» в точке x ˆ = L (неустойчивое стационарное значение) и, наконец, опять с «плюса» на «минус» в точке x ˆ 3 = (устойчивое стационарное значение) (рис..4 а). График зависимости численности популяции, описываемой моделью (.4) от времени представлен на рис..4 б. fx ( )= dx d а ˆ x() б ˆ L ˆ x = x =L x 3 = x ˆ Рис..4. Модель популяции с нижней и верхней критическими границами численности. Зависимость скорости роста популяции от ее размера (а) и динамика численности популяции (б). 3
13 Учебное пособие «Математические модели в биологии» ЗАДАЧИ К СЕМИНАРУ.. График функции, задающей скорость изменения численности микробной популяции, имеет вид: а б ) Какое выражение будет описывать динамику роста культуры, если в начальный момент времени ее размер равен 5. ) Какова будет численность культуры через час, если ее размер в начальный момент времени равна 7. Рост популяции описывается уравнением Ферхюльста. Емкость экологической ниши для нее равна. Постройте график динамики численности популяции, если известно, что начальная численность равна: а) ; б) 7; в). Скорость роста r равна.5. Укажите координаты точки перегиба и асимптоты..3. Рост популяции описывается уравнением, учитывающим нижнюю границу численности и внутривидовую dx x конкуренцию: = dx px. Определите величины d + x верхней и нижней границы численности, если известно, что коэффициент смертности равен., а внутривидовой конкуренции равен.4. Постройте графики динамики численности популяций для начальных значений меньших нижней критической границы, лежащих в пределах между нижней и верхней границей, и превышающих верхнюю границу. 3
14 СЕМИНАР 3 Дискретные модели популяций с неперекрывающимися поколениями. Дискретное логистическое уравнение. Лестница Ламерея. Модели, основанные на аппарате дифференциальных уравнений, применимы для описания динамики достаточно многочисленных популяций (например, микробных), у которых процессы рождения и гибели особей можно считать непрерывными, или у которых нет ярко выраженной сезонности периодов размножения. Если же мы имеем дело с организмами, для которых сезонность важная характеристика их жизненного цикла, то для описания динамики популяций таких видов более адекватным является аппарат конечно-разностных уравнений. Пусть численность некоторого вида в начальный момент времени равна N, по окончании одного периода времени N, по окончании двух N и.т.д. Развитие популяции во времени тогда описывается последовательностью чисел N, N, N, N, N +,. Разностным уравнением называется уравнение, которое связывает между собой значения N при различных значениях индекса. В общем виде численность популяции в определенный период времени зависит от численности на определенном предшествующем отрезке времени. В этом случае разностное уравнение имеет вид (. ) N = F N N N. (3.) n 33
15 Учебное пособие «Математические модели в биологии» + Параметры функции F в общем случае могут зависеть от конкретного периода времени. В простейшем случае, параметры среды обитания остаются неизменными, и мы приходим к уравнению с постоянными коэффициентами в правой части уравнения. Рассмотрим простую модель роста популяции, когда скорость роста в любой период времени пропорциональна размеру популяции в начале этого периода. Пусть N размер популяции в конце -го периода времени. Тогда величина N+ N выражает прирост популяции за следующий период времени, т.е. скорость роста, или рост в единицу времени, на ( + ) -м интервале времени. Эта величина должна быть пропорциональна численности N. Пусть коэффициент пропорциональности есть некоторая константа r, тогда получим разностное уравнение: N N = + rn или N+ = N( r+ ). Заметим, что это уравнение можно получить, исходя из исследованного ранее дифференциального уравнения модели экспоненциального роста (см. Семинар ) dn = rn. Скорость dn есть отношение приращения численности к приращению времени (только в отличие от не- d d прерывного случая приращение не является бесконечно Δ N N+ N N+ N малой величиной): = =. Приходим к Δ ( + ) дискретному аналогу уравнения экспоненциального роста: N + N = rn или N = ( r+ ) N, где r коэффициент вос- производства популяции. В рассмотренном примере численность популяции в конце каждого периода времени зависит лишь от ее величины по окончании предыдущего периода и не зависит от более ранних значений. В общем виде, подобный вид взаимосвязи (каждое значение в последовательности за- 34
16 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея висит только от значения на предыдущем шаге) можно описать формулой (сравните с формулой (3.)): N = или N F( N ) F( N ) =. (3.). + С помощью уравнения вида (3.) можно описывать популяции с неперекрывающимися поколениями. Например, для многих видов насекомых характерна непродолжительная жизнь взрослых особей. Взрослые особи откладывают яйца и погибают. К моменту выхода нового поколения, предыдущее поколение прекращает свое существование. К разностным уравнениям применимы понятия, используемые в теории дифференциальных уравнений. Решением (траекторией) дискретного уравнения называется любая последовательность значений ( =. ), удовлетворяющая данному дискретному уравнению при каждом значении времени, на котором уравнение определено. Различным начальным условиям соответствуют разные решения. Устойчивость решений определяется аналогично устойчивости решения дифференциального уравнения. * Равновесием называют решение вида N = cons = N, удовлетворяющее соотношению N = F( N ). (3.3) * * Устойчивость точки равновесия так же можно определить по методу Ляпунова: если при достаточно малом начальном отклонении от положения равновесия система никогда не уходит от положения равновесия, то такое положение равновесия называют устойчивым, оно соответствует устойчивому стационарному режиму функционирования системы. 35
17 Учебное пособие «Математические модели в биологии» Как и в случае с дифференциальным уравнением, для исследования устойчивости решения дискретного уравнения применим линейный анализ. * Положим N = N + x, где x отклонение от положения равновесия. Линеаризуем уравнение (3.), разлагая правую часть дискретного уравнения в ряд по степеням x в окрестности положения равновесия: df N = N + x = F N + x + o( x ). ( ) * * + + dn * N = N Учитывая определение равновесия (3.3) и отбрасывая члены порядка x и выше, получаем закон, по которому будет развиваться заданное отклонение: x + df = x. (3.4) dn * N = N Соотношение (3.4) между величинами отклонения от точки равновесия x и x + представляет собой геометрическую df прогрессию, где знаменатель прогрессии. Из dn * N = N условий сходимости геометрической прогрессии следует, что x при, если df dn * N = N , то заданное отклонение бу- 36
18 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея дет неограниченно расти: x при, и в этом случае положение равновесия будет неустойчивым. Случаи df dn * N = N = или требуют дополнительных исследований. df dn * N = N = Зная величину знаменателя геометрической прогрессии (3.4), можно сделать выводы о характере поведения траектории дискретного уравнения вблизи положения равновесия. Так, при положительных значениях знаменателя, все члены последовательности будут иметь оди- df наковый знак. Если монотонное удаление от него. При отрицательных значениях знаменателя, члены геометрической прогрессии становятся знакочередующимися. Если df 19 Учебное пособие «Математические модели в биологии» dn d ДИСКРЕТНОЕ ЛОГИСТИЧЕСКОЕ УРАВНЕНИЕ Формальная замена бесконечно малых приращений в дифференциальном уравнении логистического роста Δ N N N N N = = Δ ( + ) + + на Δ N N N rn N + = = Δ или дает следующий результат: N N+ = N + r. (3.5) N ( + r) Однако множитель + r при N > r становится отрицательным, уравнение (3.5) приводит к отрицательным значениям численности, что является с биологической точки зрения некорректным. Заметим, что в дифференциальном уравнении такого рода проблема отсутствует: множитель правой части N становится отрицательным при N >, но это дает отрицательную скорость размножения популяции (снижение размера популяции), а не отрицательную численность. Таким образом, необходимо модифицировать множитель правой части уравнения (3.5), сохранив следующие свойства: при малых значениях численности популяция растет и скорость роста не зависит от размера популяции; с течением времени численность популяции увеличивается, стремясь * к равновесному значению N =, а скорость роста стремится к нулю, оставаясь положительной. Таким свойст- r вом обладает выражение. Итак, получаем дискретный аналог логистического уравнения: e N 38
20 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея N r N N e + =. (3.6) Проведем исследование уравнения (3.6). Найдем положение равновесия: * * * N N e r N * * * * N = F( N ), т.е. =. Тогда N =, N Исследуем их устойчивость. В соответствии с аналитическим методом определения устойчивости необходимо определить знак и сравнить с величину производной правой части уравнения в точках равновесия. Производная функции равна: df dn N r = N e = N N r r r = e N e + = Nr N r = e. Подставляем значение df dn N = * N = : r r r = e = e >. =. Таким образом, при r >, состояние равновесия * N = неустойчиво, поведение траекторий в его окрестности монотонно. Подставляем значение df dn N = * N = : r r = e = r. 39
21 Учебное пособие «Математические модели в биологии» Условие df dn * N = N решение уравнения (3.6) неустойчиво. При этом, если r >, то решение немонотонно. Исследование модели логистического роста показало, что, в отличие от решения дифференциального уравнения, траектории, задаваемые его дискретным аналогом, при определенных значениях скорости прироста r обладают цикличностью, а также могут описывать различные хаотические режимы (так называемые вспышки численности). За ходом решения дискретного логистического уравнения можно проследить с помощью диаграммы (или лестницы) Ламерея. 4
22 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея ЛЕСТНИЦА ЛАМЕРЕЯ На рис. 3.. представлена зависимость численности популяции N + от численности на предыдущем шаге N, задаваемая логистическим уравнением (3.6): N r e ( ) N = N = + F N. Рис. 3.. График функции, задающей дискретное уравнение логистического роста (3.6). Пояснения в тексте. 4
23 Учебное пособие «Математические модели в биологии» N + Пунктирной линией представлена биссектриса = N. В точках пересечения графика функции F( N ) с биссектрисой выполняется равенство: N = N = + F( N), т.е. выполняется определение точки равновесия. Таким образом, точки пересечения графиков N (с координата- * ми (,)) и N (с координатами (К,К)) являются точками равновесия (см. предыдущий подраздел). * ШАГ. Пусть известна некоторая начальная численность популяции N. Какую последовательность следующих значений численностей задает логистическое уравнение? Значение N определяется равенством N = F( N), т.е. пара значений ( N, N ) является координатами соответствующей точки на графике функции F( N ) (рис. 3. а). Отложим на координатной плоскости ( N, ) точки (, N ) и (, N ) (рис. 3. б). ШАГ. Следующее значение численности N определяется из соотношения N = F( N) (рис. 3. в). На графике, величина N из значения функции должна стать значением аргумента: проводим перпендикуляр от точки (, N ) до пересечения с биссектрисой, затем опускаем перпендикуляр до оси абсцисс N. ШАГ 3. Повторяем шаг. Теперь наша начальная точка точка N, значение численности N есть ордината точки на графике функции F( N ): ( N, F( N ) ) (рис а, б). 4
24 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея ШАГ 4. Повторяем шаг. Значение N переносим на ось абсцисс с помощью отражения от биссектрисы (рис. 3.3 в). ШАГ 5. Повторяем шаг. Следующее значение численности N 3 определяем как ординату точки на графике функции F: (, ( )) N F N (рис. 3.4 а, б). Продолжая повторять шаги построения лестницы Ламерея, получим последовательность значений численности популяции в разные моменты времени. В рассмотренном примере мы получили, что со временем численность в виде затухающих колебаний сходится к равновесному значению (рис , 3.7 в). Характер последовательности значений численности популяции, полученной при помощи лестницы Ламерея, может быть монотонным, циклическим, колебательным и хаотическим. Каким он будет, в каждом конкретном случае определяется формой кривой F( N ). В свою очередь, форму кривой определяют значения параметров функции F( N ) (скорость прироста r и емкость экологической ниши ). 43
25 Учебное пособие «Математические модели в биологии» а а б б в в Рис. 3.. Построение лестницы Ламерея. Рис Построение лестницы Ламерея. Продолжение. 44
26 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея а а б б в в Рис Построение лестницы Ламерея. Продолжение. Рис Построение лестницы Ламерея. Продолжение. 45
27 Учебное пособие «Математические модели в биологии» а а б б в в Рис Построение лестницы Ламерея. Продолжение. Рис Построение лестницы Ламерея. Окончание. 46
28 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея ЗАДАЧИ К СЕМИНАРУ С помощью диаграммы Ламерея построить график динамики численности популяции, если зависимость N+ = f( N) имеет вид: а б в г 47
Видео:Аллюзии трейдинга 5. Размножение кроликов или Уравнение Ферхюльста.Скачать

Дифференциальные модели в экономике, биологии и медицине
В этом параграфе мы разберем несколько классических моделей, предложенных за последние 200 лет в различных областях науки: экономике, биологии и медицине. Общим при построении этих моделей является использование дифференциальных уравнений с разделяющимися переменными, которые несложно решить, прочитав §59 данного справочника.
п.1. Экономика. Равновесная цена в модели Вальраса
Начальные сведения о модели рыночного равновесия, кривых спроса и предложения – см. §18 справочника для 9 класса.
Рассмотрим поведение рыночной цены при небольшом отклонении от точки равновесия по методу, предложенному Леоном Вальрасом (1874 г.)
Пусть p — цена товара, D(p) — спрос на него, S(p) — предложение.
Пусть спрос и предложение на рынке уравновешены, равновесная цена равна (p_0).
Если спрос начнет немного превышать предложение, то цена начнет расти: $$ frac
=0, D(p_0)-S(p_0)=0 $$ Разложим каждую из функций с помощью дифференциала (см. §52 данного справочника) с точностью до линейного множителя: begin D(p)approx D(p_0)+D'(p_0)(p-p_0)\ S(p)approx S(p_0)+S'(p_0)(p-p_0) end Тогда разность спроса и предложения: begin D(p)-S(p)approx D(p_0)+D'(p_0)(p-p_0)-S(p_0)-S'(p_0)(p-p_0)=\ =underbrace_+left(D'(p_0)-S'(p_0)right)(p-p_0)=left(D'(p_0)-S'(p_0)right)(p-p_0) end Получаем уравнение с разделяющимися переменными: begin frac
Например:
Пусть (D(p)=9-frac
, S(p)=frac
)
(sqrt=y’x) — ДУ первого порядка первой степени
Тогда равновесная цена (9-frac
=frac
Rightarrow frac
=9Rightarrow p_0^2=36Rightarrow p_0=6)
Значения производных: begin D'(p)=0-frac=-frac p3, D'(p_0)=-2\ S'(p)=frac, S'(p_0)=1 end Изменение цены со временем в этом случае: $$ p(t)=6+(p(0)-6)e^=6+(p(0)-6)e^ $$ Построим графики для трех различных цен в начальный момент времени: $$ p(0)=left $$ (p(0)=5: p(t)=6-e^)
(p(0)=7: p(t)=6+e^)
(p(0)=9: p(t)=6+3e^)
Все три кривые постепенно сходятся к равновесной цене (p_0=6).
Устойчивое схождение к (p_0) будет наблюдаться только при условии: $$ D'(p_0)-S'(p_0)lt 0 $$ Т.е кривая спроса должна быть более крутой в своем спуске, чем кривая предложения на подъеме. Говорят, что эластичность спроса по цене в точке равновесия должна быть выше, чем эластичность предложения по цене.
Если степень при экспоненте будет положительной, (D'(p_0)-S'(p_0)gt 0) решение уходит на бесконечность. Говорят, что такое решение неустойчиво.
Если степень при экспоненте будет равна нулю, (D'(p_0)-S'(p_0)=0), цена не будет меняться и останется неравновесной.
п.2. Биология. Логистическое уравнение Ферхюльста для роста популяции
Пусть (P(t)) – численность популяции. Построим модель её изменения со временем.
Логично предположить, что прирост потомства в популяции пропорционален количеству особей, из чего получаем:
| Закон Мальтуса (1798 г.): $$ frac |
Решением этого уравнения будет (P(t)=P_0e^
| Закон Ферхюльста (1838 г.): $$ frac (K)- максимальный размер популяции в условиях ограниченных ресурсов. |
| Решение уравнения Ферхюльста (логистическая кривая): $$ P(t)=frac<KP_0e^ |
Например:
Пусть популяция растет со скоростью (r=0,1) тыс/год
Начальное количество особей (P_0=1) тыс
Максимальное количество, которое способна прокормить данная территория, (K=10) тыс
Модель показывает, что через 70 лет популяция займет всю нишу, и её рост фактически прекратится.
На начальном этапе преобладает r-стратегия: бурное размножение и короткая продолжительность жизни.
Исчерпание ресурсов заставляет переходить на K-стратегию: низкий темп размножения и долгую жизнь.
Экспериментально рост популяции по кривой Ферхюльста был подтвержден в лабораторных условиях для мух-дрозофил. В естественных условиях для животных – и тем более, в рамках социума для людей – закономерность нарушается.
п.3. Медицина. Модель развития эпидемии SIR
Традиционной моделью, описывающей процесс развития эпидемии, является модель SIR (Susceptible/Infected/Recovered), предложенная У. Кермаком и А. Маккендриком в 1927 г.
Вся популяция в модели делится на три группы:
- (S(t))— восприимчивые к инфекции, здоровые на момент времени (t);
- (I(t))— уже инфицированные;
- (R(t))— выздоровевшие, больше невосприимчивые к инфекции.
Популяция считается постоянной, т.е. (N=S(t)+I(t)+R(t)=const).
Рождаемость и смертность не учитывается.
Получаем следующую систему дифференциальных уравнений: $$ begin frac
Начальные условия в момент времени (t=0): $$ S(0)=S_0geq 0, I(0)=I_0geq 0, R(0)=R_0geq 0 $$ Переход из одной группы в другую можно изобразить линейной схемой:

| № | Переход одного человека из одной группы в другую | Скорость перехода |
| 1 | $$ (S;I)rightarrow (S-1; I+1) $$ | $$ betafrac $$ |
| 2 | $$ (I;R)rightarrow (I-1; R+1) $$ | $$ gamma I $$ |
Полученная система уравнений не является линейной и не имеет точного аналитического решения. Но её можно решить с использованием численных методов.
$$ begin frac=-betafrac\ frac=betafrac-gamma I(t)\ frac=gamma I(t) end $$ Считаем (triangle t=1) – следующий шаг итерации. Тогда: $$ begin S_-S_i=-betafrac\ I_-I_i=betafrac<S_I_i>-gamma I_i\ R_-R_i=gamma I_ end $$ Получаем следующий итеративный процесс: $$ begin S_=left(1-betafracright)S_i\ I_=left(1+betafrac<S_>-gamma right)I_i\ R_=gamma I_+R_i end $$ Знаний по информатике вам должно хватить, чтобы написать небольшой скрипт с циклом для этих уравнений и построить график.
Например:
Пусть общее количество населения N=10 тыс.чел.
В начальный момент инфицирован 1% населения: $$ S(0)=0,99N, I(0)=0,01N, R(0)=0 $$ Параметры: (beta=0,128; gamma=0,096) в расчете на день (эти параметры были рассчитаны по фактическим данным для лихорадки Эбола в Сьерра-Леоне).
Результат моделирования в MATLAB:
Красная кривая – это количество болеющих в данный момент. Как мы видим, к концу года она стремится к 0. Пик приходится на 70-80 дней с начала эпидемии и составляет 413 чел. или 4,13% населения.
Зеленая кривая – количество переболевших, к концу года выходит на асимптоту в 4700 чел. или 47,0% населения.
Синяя кривая – количество так и не заболевших, к концу года спускается на асимптоту в 5300 чел. или 53,0% населения.
Чем больше больных у вас будет в начале эпидемии и чем больше параметр (beta), тем выше будет пик (I_) для болеющих. Также, количество переболевших в конце эпидемии будет больше количества не заболевших.
Модель SIR – это начальный этап для исследований. На практике для моделирования эпидемий могут использоваться модели с десятками переходов и параметров, с постепенным усложнением по мере накопления данных.
📹 Видео
Обучение Трейдингу - Выпуск 3. Логистическая криваяСкачать

Геометрический смысл производной. Уравнение касательнойСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Linear Regression vs. Logistic Regression [in 60 sec.] #shortsСкачать
![Linear Regression vs. Logistic Regression [in 60 sec.] #shorts](https://i.ytimg.com/vi/FLmfPbP0Bac/0.jpg)
Откуда появляются дифференциальные уравнения и как их решатьСкачать

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Дифференциальные уравнения, Ремизов А. О., лекция 1, 01.09.2023Скачать

Logistic MapСкачать

Can we use Mean square error as a cost function in logistic regression#datascienceinterviewquestionsСкачать

Logistic Curve Method | S-Curve | Population Forecasting | Environment Engineering | Quick RevisionСкачать

Жизнь, смерть и дифференциальные уравненияСкачать

№9. Элементы вариационного исчисления. Уравнения Лагранжа-Эйлера.Скачать

Динамика биологических популяций 1Скачать

Модели роста популяцийСкачать

What are the assumptions of logistic regression? #datascienceinterviewquestions #machinelearningСкачать

Logistic Regression CLASSIFIER has REGRESSION in its name? #InterviewQuestions #AVshortsСкачать





