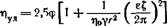Уравнение эйнштейна для вязкости условия (3 видео)

Вязкость дисперсных систем

Важной характеристикой структурно-механических свойств является течение. Течение бывает ламинарным и турбулентным.

Ламинарное течение – движение жидкости в виде параллельных слоев, имеющих различную скорость и не смещающихся между собой. Возникает при низкой скорости течения и малом перепаде давления.

Турбулентное течение – течение, сопровождающееся вихреобразованием.

В соответствие с уравнением Ньютона сила сопротивления при течении F прямо пропорциональна градиенту скорости du и площади поверхности потока S:

— уравнение Ньютона

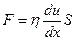
где η – коэффициент пропорциональости или вязкость, зависит от природы жидкости Единицей измерения вязкости является пуаз (пз), 1 пз = Па∙с= Н∙с/м 2 . Единица измерения вязкости названа в честь франц. учёного Пуазейля, который впервые изучал движение жидкости в капиллярах.

Ламинарное течение по трубкам или скорость течения жидкости из капилляра описывается уравнением Пуазейля (1842г.), которое было найдено экспериментальным путём:

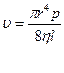
где u — объемная скорость течения;

r – радиус капилляра трубки;

Δp – перепад давления или разность давления на обоих концах трубки;

Η – вязкость жидкости;

l – длина капилляра.

Величина, обратная вязкости называется текучестью – характеризует подвижность жидкости под влиянием внешних воздействий.

Жидкости, у которых отсутствует зависимость вязкости от характера взаимодействия частиц, подчиняются законам Ньютона и Пуазейля и называются ньютонскими жидкостями. Уравнение Ньютона и Пуазейля соблюдается, если жидкость движется ламинарно.

Вязкость дисперсных систем всегда превышает вязкость чистой дисперсионной среды. Зависимость вязкости коллоидной системы от концентрации дисперсной фазы выражается уравнением Эйнштейна (1906г.):

— уравнение Эйнштейна,

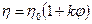
где η – вязкость коллоидной системы;

η₀ – вязкость чистого растворителя (дисперсионной среды);

φ – объемная доля частиц дисперсной фазы;

k – коэффициент, характеризующий форму частицы. Для сферической формы k = 2,5.

Для структурированных систем законы Ньютона не выполняются.

Содержание

Лако-красочные материалы — производство
Технологии и оборудование для изготовления красок, ЛКМ
ЗАВИСИМОСТЬ ВЯЗКОСТИ КОЛЛОИДНЫХ СИСТЕМ ОТ КОНЦЕНТРАЦИИ ДИСПЕРСНОЙ ФАЗЫ
4.1.2. Вязкость разбавленных дисперсных систем
🎦 Видео

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Лако-красочные материалы — производство

Видео:Относительность 19 - Уравнение ЭйнштейнаСкачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

ЗАВИСИМОСТЬ ВЯЗКОСТИ КОЛЛОИДНЫХ СИСТЕМ ОТ КОНЦЕНТРАЦИИ ДИСПЕРСНОЙ ФАЗЫ

Вязкость коллоидных систем всегда выше вязкости чистой дисперсионной среды. Эйнштейн в 1906 г., исходя из чисто гидродинамических представлений, вывел уравнение, устанавливающее связь между вязкостью системы rj. и концентрацией дисперсной фазы:

11 = т1о(1 +2,5Ф) (X, 17)

Где Т]0 — вязкость дисперсионной среды; ф — объемная концентрация дисперсной фазы.

Уравнение (X,17) пригодно только при условии, что взвешенные в жидкости частицы являются твердыми шарообразными телами, концентрация дисперсной^ фазы сравнительно невелика и между частицами отсутствуют взаимодействия. Кроме того, для

Соблюдения уравнения Эйнштейна необходимо, чтобы система была несжимаема, течение жидкости носило ламинарный характер, между частицами и жидкостью отсутствовало скольжение и, наконец, чтобы частицы были велики по сравнению со свободным пробегом молекул среды, но малы по сравнению с пространством, в котором происходит течение.

Значение численного коэффициента в уравнении (X, 17) зависит от формы частиц. Поэтому в общем виде уравнение Эйнштейна можно записать так:

Где а — множитель, зависящий от формы частиц.

Уравнение Эйнштейна часто пишут также следующим образом:

(тіЛіо) — 1 = (ті — чіо)/тіо = a

Где ti/tjo — отношение вязкости системы к вязкости среды (относительная вязкость) ; п — общее число частиц в системе; о — объем одной частицы дисперсной фазы; V — объем системы, мл. ‘

Величину (т] — Ло)/»По. характеризующую относительное увеличение вязкости дисперсионной среды при введении в нее определенного количества дисперсной фазы, не совсем правильно называют удельной вязкостью. Ее обычно обозначают символом т]уд. Из предыдущего следует, ЧТО

Из всего сказанного следует, что, по Эйнштейну, между вязкостью системы и содержанием в ней дисперсной фазы должна су-» ществовать прямолинейная зависимость. Весьма существенно также, что, согласно Эйнштейну, вязкость не зависит от дисперсности суспензии.

Экспериментальную проверку уравнения Эйнштейна проводили Банселен на суспензиях гуммигута, Оден на золях серы и наиболее обстоятельно Эйрих на суспензиях мельчайших стеклянных шариков, шарообразных спор грибов и дрожжевых клеток. Во всех этих исследованиях при сферической форме частиц и малых концентрациях дисперсной фазы численный коэффициент при (р имел значение, близкое к 2,5. Отклонения наблюдались, когда частицы не были шарообразны, концентрация дисперсной фазы в суспензии была значительной и между частицами существовали электрические или другие силы взаимодействия.

Влияние анизодиаметричности частиц. При палочкообразной, эллипсоидной или пластинчатой форме частиц суспензии вязкость системы всегда больше, чем должна быть согласно уравнению Эйнштейна. Причина этого заключается в том, что жидкость, попадающая в объем (эллипсоид вращения), образующийся вокруг нешарообразных частиц, находящихся в интенсивном броуновском движении, становится как бы связанной с частицей. В результате

Этого возникает кажущееся увеличение объемной доли дириерсной фазы в системе, что и приводит к повышению вязкости.

Экспериментально показано, что вязкость суспензии С малыми анизодиамет — рическими частицами, находящимися обычно в интенсивном броуновском движении, повышается пропорционально квадрату отношения большой и малой осей эллипсоида вращения, а вязкость суспензии с достаточно большими нешарообразными частицами, совершающими медленное броуновское движение, возрастает лишь прямо пропорционально отношению осей.

Теоретические вычисления, проведенные Куном, Симха и другими исследователями с использованием в качестве моделей частиц самой разнообразной формы, весьма сложны и не всегда убедительны. Поэтому до сих пор еще иет общей теории зависимости вязкости коллоидных систем от формы частиц.

Вязкость систем, содержащих анизодиаметрические частицы, как мы видели, зависит от скорости течения. Вытянуты^ частицы ориентируются в потоке, вращательное движение их затрудняется и в результате этого вязкость системы с увеличением скорости течения снижается. Подобное явление можно наблюдать, например, при измерении вязкости золя V2O5, частицы которого сильно ани- зодиаметричны.

Влияние истинной концентрации дисперсной фазы и сольватации. Отличие вязкости концентрированной дисперсной системы от значений вязкости, вычисленной по уравнению Эйнштейна, объясняется тем, что в жидкости около частиц возникают взаимовозму — щающие микропотоки, затрудняющие движение системы. Дебройн считает, что при этом, помимо гидродинамических взаимодействий, необходимо учитывать также и механические (столкновения частиц, образование пар и т. д.).

При очень малых концентрациях суспензии поток, возникающий вокруг одной частицы, очень мало влияет на потоки, возникающие около других частиц, и на скорость движения всего потока жидкости в целом. Однако с увеличением концентрации дисперсной фазы это влияние все увеличивается и приводит к отклонению от закона Эйнштейна.

Другое объяснение отклрнения вязкости дисперсных систем от значений, найденных с помощью уравнения Эйнштейна, заключается в сольватации частиц. Явление сольватации может объяснить и часто наблюдающуюся зависимость вязкости от дисперсности системы при одинаковой объемной концентрации дисперсной фазы.

Влияние сольватации можно представить следующим образом. Если к поверхности шарообразной частицы радиусом г прилип слой дисперсионной среды толщиной H, то влияющий на вязкость эффективный объем частицы (объем самой частицы вместе с объемом сольватного слоя) составляет 4/зя(г + /г)3. Для значений H, малых по сравнению с г, будем иметь 4/зЯ(г3 + 3/»2/г). Соответственно этому при вычислении эффективной объемной концентрации дисперсной фазы ф за объем дисперсной фазы следует принять не величину 4/3 nr3v, а 4/зя(г3+3r2ft)v (где v — численная концентрация). Если принять истинный объем дисперсной фазы ф0 = 4/злг, то для ф получаем:

Следовательно, .величина ф окажется больше объема дисперсной фазы фо, и эта величина будет тем больше, чем меньше частицы. Иными словами, вязкость возрастает с уменьшением размера частиц зеля. Подобное возрастание иязкости при повышении степени дисперсности золя серы наблюдал Свен Оден.

Фикенчер и Марк для учета влияния сольватации предложили модифицировать уравнение Эйнштейна, введя в него соответствующую поправку. Согласно этим авторам, в уравнении Эйнштейна, так же как и в уравнении Ван-дер-Ваальса, вместо общего объема системы следует ввести эффективный объем, т. е. объем системы за вычетом объема частиц. Так как частицы в системе находятся в сольватированном состоянии и, кроме того, совершают броуновское движение, описывая некие тела вращения, то объем дисперсионной среды, энергетически и стерически связанной с частицами, также следует причислить к объему дисперсной фазы. Тогда уравнение (X, 18) примет вид:

Где о’ — объем частицы имеете с энергетически и стерически связанной с ней средой.

Уравнение Фикенчера и Марка хорошо объясняет, почему в некоторых случаях вязкость возрастает с увеличением концентрации дисперсной фазы быстрее, чем это должно быть в соответствии с прямолинейной зависимостью. Действительно, с увеличением концентрации дисперсной фазы в растворе возрастает пропорциональная ей величина п в числителе и одновременно уменьшается величина (V — Nv‘) в знаменателе, что и приводит к более быстрому возрастанию вязкости, чем концентрации.

Влияние взаимодействия между частицами. Причина неприменимости в некоторых случаях уравнения Эйнштейна к дисперсным системам может заключаться в проявлении сил притяжения между коллоидными частицами. При этом в системе образуются более или менее рыхлые структуры, которые включают значительные объемы дисперсионной среды. Подобная иммобилизация, т. е. уменьшение подвижности растворителя, приводит к тому, что вязкость системы оказывается гораздо больше той, которая может быть вычислена по уравнению Эйнштейна. Вязкость в таких системах сильно зависит от скорости течения, так как представляет собой структурную вязкость, обусловленную наличием в системе рыхлых пространственных сеток.

. С другой стороны, непрйменимость уравнения Эйнштейна к коллоидным системам может быть связана и с проявлением сил отталкивания между частицами, несущими одноименный электрический заряд. Согласно Смолуховскому, вязкость золей с заряженными частицами выше вязкости золей с незаряженными частицами. Повышение вязкости в результате наличия на поверхности частиц двойного электрического слоя называется электровязкостным Эф* Фектом.

Смолуховский вывел следующее уравнение, связывающее удельную вязкость золя с электрокинетическим ^-потенциалом двойного электрического слоя частиц:

Где т]о — вязкость дисперсионной среды; у — удельная электропроводность; г — радиус частиц; е — диэлектрическая проницаемость

Поправочный член в уравнении (X, 22) может иметь весьма большое значение. Подсчеты показывают, что для золей, радиус частиц которых равен 10_6 см, а электропроводность у = — Ю-4 Ом-1-см-1, поправочный член может быть в 10 раз больше основного.

Согласно уравнению Смолуховского, вязкость коллоидных систем при введении электролитов должна уменьшаться как вследствие снижения ^-потенциала, так и в результате увеличения электропроводности межмицеллярной жидкости. В изоэлектрическом состоянии золя (при % = 0) уравнение Смолуховского переходит в уравнение Эйнштейна. Следует, однако, отметить, что при астабилизации коллоидной системы введением в нее электролита (вследствие уменьшения сил отталкивания между частицами в золе) возможны явления агрегации частиц, приводящие к образованию структур и появлению структурной вязкости, что не предусмотрено уравнением Смолуховского. В результате этого понижение ^-потенциала частиц золя в определенных условиях может не только не вызывать понижения вязкости золя, но и обусловить ее повышение.

Буутс в 1948 г. вывел уравнение для электровязкостного эффекта, существенно отличающееся от уравнения Смолуховского. Согласно Буутсу, величина электровязкостного эффекта значительно меньше, чем об этом можно судить по уравнению Смолуховского, и независимо от значения ^-потенциала становится ничтожной, когда толіЦииа двойного электрического слоя очень мала по сравнению с радиусом частиц.

Видео:Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

4.1.2. Вязкость разбавленных дисперсных систем

Если в разбавленных дисперсных системах (при отсутствии взаимодействия между диспергированными частицами) размер частиц оказывается значительно большим, чем размер молекул жидкости, но намного меньшим, чем радиус капилляров, по которым такая жидкость течет, то макроскопическая вязкость, измеренная каким-либо методом, будет отличаться от вязкости чистой жидкости, хотя течение такой системы может быть описано законом Ньютона. Происходит это потому, что частица, по своим размерам намного превосходящая молекулы жидкости, искажает картину течения слоев жидкости.

Для сферических частиц расчет вязкого сопротивления потока жидкости, в котором находятся сферические частицы, был проведен Стоксом.

Для несжимаемых гладких сферических частиц, движущихся вдали от стенок капилляра так, что плоскость разрыва между частицей и жидкой фазой проходит в жидкости, сила, уравновешивающая силу потока на неподвижную частицу, составит

где r – радиус частиц, U₀ – скорость движения частицы относительно жидкости, h – вязкость жидкости.

Сила трения и коэффициент вязкого сопротивления движению асимметричных частиц зависит от ориентации таких частиц в потоке жидкости. Существует ряд уравнений для расчета коэффициента трения В для частиц различной формы.

Влияние частиц дисперсной фазы на вязкое течение жидкостей будет состоять в том, что те слои, которые прилегают непосредственно к частицам, могут перемещаться только с той же скоростью, что и частицы. Этот эффект был рассчитан Эйнштейном (1906 г.) для сферических частиц. Принимая, что на достаточном удалении от поверхности частицы поток имеет постоянную скорость, а сама частица перемещается вместе с потоком, Эйнштейн получил уравнение для вязкости дисперсной системы

где h – вязкость дисперсной среды; j – объемная доля частиц дисперсной фазы; 2,5 – коэффициент формы сферических частиц; h_отн= h/h₀– относительная вязкость.

Симха распространил метод Эйнштейна на дисперсии с частицами, имеющими форму, отличающуюся от сферической при низких градиентах скорости течения, когда частицы ориентированы длинной осью параллельно течению, получил уравнение

гдеu – коэффициент формы частиц; для асимметричных частиц всегда больше 2,5.

При больших градиентах скорости течения частицы могут располагаться беспорядочно, в том числе и поперек течения, что приводит к образованию локальных турбулентных областей, для таких дисперсий характерно неньютоновское течение.

Уравнение (2.4.16), известное как уравнение Симха-Эйштейна, общее как для сферических, так и для несферических частиц, часто записывают в форме

где h_уд– удельная вязкость – безразмерная величина, показывающая приращение вязкости относительно вязкости дисперсионной среды, приходящееся на дисперсную фазу.

Можно отметить, что удельная вязкость зависит только от общего объема, занятого дисперсной фазой и не зависит от размера частиц и их распределения по размерам.

Для разбавленных эмульсий, в которых сферические капли жидкости имеют вязкость h’, Тейлор получил уравнение

. (2.4.18)

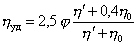
Для дисперсных систем, где возможно парное взаимодействие частиц, приводящее к образованию ориентированных вдоль потока временных агрегатов частиц, Симха предложил уравнение, описывающее вязкость систем со сферическими частицами, в котором взаимодействие между частицами и возможные их столкновения при течении дисперсии учитываются дополнительным членом:

h_уд = 2,5j + 12,6j 2 . (2.4.19)

Более точным считается теоретическое уравнение Ванда, полученное для дисперсий, в которых образуются агрегаты из двух частиц. В нем не учитывается рассеивание энергии, возможное при столкновении частиц в потоке,

h_уд = 2,5j + 7,34j 2 . (2.4.20)

Это уравнение нашло экспериментальное подтверждение при изучении поведения стеклянных сфер в водно-глицериновой среде с высокой вязкостью. В водной среде был найден коэффициент для второго члена уравнения (2.4.19), равный от 9 до 13, что согласуется как с уравнением Ванда, так и с уравнением Симха.

В общем виде можно записать уравнение зависимости вязкости дисперсии от объемной концентрации дисперсной фазы в виде

h/h₀=1 + aj + bj 2 + cj 3 +.

h_уд=aj + bj 2 + cj 3 +. (2.4.21)

Это уравнение позволяет учесть все виды взаимодействий, возникающих при течении дисперсных систем. Можно отметить, что при концентрации дисперсной фазы менее 1% при расчете второго члена уравнения (2.4.21) относительная вязкость даже при наибольшем значении постоянной b вносит поправку не более 0,1% от найденной относительной вязкости, что находится в пределах экспериментальной погрешности. Естественно, что при более высокой концентрации дисперсной фазы необходимо учитывать второй член уравнения, а при необходимости высокой точности определения вязкости дисперсий — и третий.

Уравнение (2.4.21) можно использовать и для расчета вязкости несферических частиц в зависимости от концентрации.

Для таких систем уравнение зависимости вязкости от концентрации принимает вид

где а – параметр, зависящий от формы частиц; K₁, K₂, K₃. – безразмерные постоянные.

Постоянная а рассчитывается как отношение длинной оси несферических частиц к короткой.

Постоянные уравнений (2.4.21) и (2.4.22) зависят не только от формы частиц, но и от градиента скорости течения, так как при низких скоростях течения броуновское движение частиц создает большое сопротивление течению, особенно если асимметричные частицы ориентируются поперек потока. В этой связи экспериментально найденная вязкость дисперсных систем с постоянной концентрацией уменьшается при повышении скорости сдвига даже в том случае, если в дисперсии не образуется пространственная структура. Приведенные выше уравнения справедливы для дисперсных систем, в которых на поверхности частиц не образуется двойной электрический слой или в которых не развита его диффузионная часть.

Если же на поверхности частиц образуется двойной ионный слой диффузионной структуры, то в процессе течения диффузионная обкладка может отрываться от частиц, в результате чего частицы приобретают нескомпенсированный заряд и течение может тормозиться в результате электростатического взаимодействия. Этот эффект, называемый электровязкостным, учитывается добавочным членом в уравнении Эйнштейна (2.4.14)

, (2.4.23)

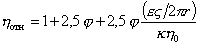
где e – диэлектрическая проницаемость среды; z – электрокинетический потенциал; r – радиус частиц; k – удельная электрическая проводимость среды; h₀ – вязкость дисперсионной среды.

Уравнение (2.4.23) в 1916 г. предложил Смолуховский для жестких не набухающих частиц. При развитых диффузионных слоях для частиц с r» 10 -8 м при k» 10 -4 Ом -1 ×cм -1 поправочный член может быть на порядок больше основного.

При введении электролитов и следующим за этим сжатием двойного ионного слоя вязкость падает до некоторого предельного значения, не зависящего от вида добавленного электролита.

Экспериментальная проверка уравнения (2.4.23) показала, что найденные экспериментальные значения вязкости в 100 раз меньше рассчитанного по уравнению Смолуховского. В связи с этим были предложены другие уравнения, учитывающие электровязкостный эффект, в частности, известное уравнение Буфа:

, (2.4.24)

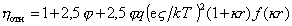
где q – постоянная, зависящая от температуры и природы электролита; е – элементарный заряд; k – параметр Дебая, характеризующий толщину двойного ионного слоя; f(kr) – параметр, зависящий от размера частиц и толщины двойного ионного слоя.

Уравнение Буфа более точно учитывает электровязкостный эффект и теоретически предсказывает порядок величины вязкости. Рассчитанные по этому уравнению и найденные экспериментально значения вязкости имеют один порядок, но различаются по величине в 2-3 раза.