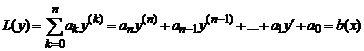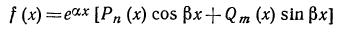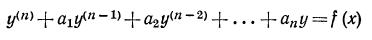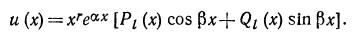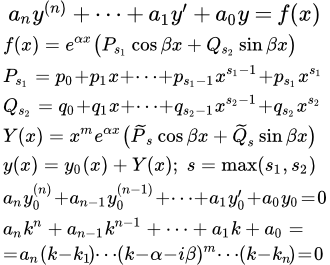Подбор частного решения неоднородного уравнения при специальном виде правой части

Видео:Видеоурок "Нахождение частных решений по виду правой части"Скачать

Уравнения с правой частью специального вида

Общее решение y_ОН линейного неоднородного дифференциального уравнения L(y)=b(x) есть сумма общего решения y_ОО соответствующего однородного уравнения L(y) = 0 и какого — либо частного решения y_ЧН исходного неоднородного уравнения. Для уравнений с постоянными коэффициентами и правой частью специального вида это частное решение может быть найдено достаточно просто.

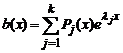
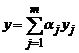
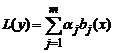
Функцию , где P_j(x) — некоторые полиномы (многочлены), назовём квазиполиномом. По теореме о наложении решений, если y_j , j=1,2. m — решения уравнений L(y) = b_j(x), то есть решение уравнения . Поэтому, не умаляя общности, будем считать, что правая часть уравнения L(y) = b(x) с постоянными коэффициентами имеет вид b(x) = P(x)e λx . В частности, если λ=α+βi — комплексное число, то наиболее общей правой частью указанного типа является функция

(1)

у которой P(x)и Q(x)- некоторые полиномы. Справедлив следующий результат.

Теорема. Линейное дифференциальное уравнение

с постоянными коэффициентами и правой частью вида (1) имеет частное решение

,

где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x) , S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x) , Q(x).

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Метод подбора частного решения.

Структура общего решения линейного неоднородного уравнения, т.е. уравнения с правой частью:

определяется следующей теоремой:

Если u = u (x) — частное решение неоднородного уравнения, а y₁ , y₂ , . . . , y_n – фундаментальная система решений соответствующего однородного уравнения, то общее решение линейного неоднородного уравнения имеет вид y = u + C₁y₁ + C₂y₂ + . . . + C_ny_n; иными словами, общее решение неоднородного уравнения равно сумме любого его частного решения и общего решения соответствующего однородного уравнения.

Следовательно, для построения общего решения неоднородного уравнения надо найти одно его частное решение (предполагая уже известным общее решение соответствующего однородного уравнения).

Метод подбора частного решения (метод неопределенных коэффициентов). Этот метод применим только к линейным уравнениям с постоянными коэффициентами и только в том случае, когда его пра­вая часть имеет следующий вид:

(или является суммой функций такого вида). Здесь а и β — постоянные, Р_п (х) и Q_т(x) — многочлены от х соответственно n-й и т-й степени.

Частное решение уравнения n-го порядка

(где f (х) имеет указанный вид, а a₁ , a₂ , . . . , a_n — действительные постоянные коэффициенты) следует искать в виде

Здесь r равно показателю кратности корня α + βi в характеристическом уравнении

(если характеристическое уравнение такого корня не имеет, то следует положить r = 0);

P_l (x) и Q_l (x) — полные многочлены от х степени l с неопределенными коэффициентами, причем l равно наибольшему из чисел п и т (1 = п≥т, или l = m≥n):

Неопределенные коэффициенты можно найти из системы линейных алгебраических уравнений, получаемых отождествлением коэффициентов подобных членов в правой и левой частях исходного уравнения после подстановки в него и (х) вместо у.

Проверку правильности выбранной формы частного решения дает сопоставление всех членов правой части уравнения с подобными им членами левой части, появившимися в ней после подстановки и (х).

Если правая часть исходного уравнения равна сумме нескольких различных функций рассматриваемой структуры, то для отыскания частного решения такого уравнения нужно использовать теорему наложения решений: надо найти частные решения, соответствующие отдельным слагаемым правой части, и взять их сумму, которая и является частным решением исходного уравнения (т. е. уравнения с суммой соответствующих функций в правой части).

Частными случаями функции f (х) рассматриваемой структуры (при наличии которых в правой части уравнения применим метод подбора частного решения) являются следующие функции:

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Определение общего решения по известному частному решению

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) ,
где – действительные числа; – действительная функция. Если известно частное (любое) решение уравнения (1), то можно найти его общее решение по формуле:
,
где – общее решение однородного уравнения:
.

Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.

Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью

Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) ,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.

Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.

Вначале ищем общее решение однородного уравнения:
(3) .

Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.

После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.

Видео:Метод неопределенных коэффициентов для линейного ДУ со специальной правой частью (квазимногочленом)Скачать

Установление вида частного решения

Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) .
Решаем это уравнение. Получаем n корней . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) .

Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень через действительную и мнимую части:
.
Для действительного корня .

Некоторые корни в (5) могут быть кратными:
.
Здесь p – кратность корня. Кратный корень кратности p входит в произведение (5) в виде множителя .

Если среди корней характеристического уравнения (4) нет корня со значением
,
то частное решение уравнения (2) имеет вид:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами , которые подлежат определению подстановкой в уравнение (2).

Если среди корней характеристического уравнения (4) есть корень кратности p со значением

то частное решение уравнения (2) имеет вид:
,
где также – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
.

Видео:ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать

Частные случаи

Неоднородность в виде многочлена

Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
,
где – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.

Если среди корней характеристического уравнения (4) нет нулевого корня
,
то частное решение имеет вид:
.
То есть оно является многочленом степени s с неопределенными коэффициентами .

Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде произведения экспоненты и многочлена

Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.

Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде суммы произведений многочленов на косинус и синус

Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней на косинус и синус:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет чисто мнимого корня со значением iβ :
,
то частное решение является суммой произведений многочленов, косинуса и синуса:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
,
то частное решение имеет вид:
.
То есть частное решение как и в предыдущем случае, но умноженное на .

Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 14-09-2020

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Подбор частного решения неоднородного уравнения при специальном виде правой части

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид полинома от x степени m

Для уравнения с постоянными коэффициентами в случае, когда правая часть имеет специальный вид, удается найти частное решение методом неопределенных коэффициентов (методом подбора частных решений).

Рассмотрим этот метод для уравнения n-го порядка вида

где a₁, …, a_n — действительные числа, α — действительное число, P_m (x) — полином от x степени m, которая может быть равной нулю, так что этот полином может вырождаться в число, отличное от нуля.

Метод неопределенных коэффициентов состоит в том, что задается вид частного решения с неопределенными коэффициентами, которые определяются подстановкой в данное уравнение. Вид частного решения уравнения зависит от того, совпадает ли число α с корнями характеристического уравнения:

Если α не является корнем характеристического уравнения, то частное решение имеет вид

где Q_m (x) — полином степени m с коэффициентами, подлежащими определению.

Если α является корнем характеристического уравнения кратности k, то

т. е. частное решение приобретает множитель x k .

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид:

где α и b — действительные числа, P₁ и P₂ — полиномы от x, старшая степень которых равна m, так что один из них обязательно имеет степень m, а степень другого не превосходит m, и он может быть даже тождественно равен нулю.

Составим комплексное число α + ib, где действительная часть α есть коэффициент показателя множителя e αx , а мнимая часть b — коэффициент аргумента bx функций cos bx и sin bx.

Укажем вид частного решения уравнения (14.2) в двух случаях:

Если число α + ib не является корнем характеристического уравнения, то

где Q₁ и Q₂ — полиномы степени m с неопределенными коэффициентами; причем надо брать оба эти полинома даже в том случае, когда один из полиномов P₁ и P₂ тождественно равен нулю.

Если число α + ib есть корень характеристического уравнения кратности k, то

т. е. частное решение приобретает множитель x k .

ПРИМЕР 15.2. Найти общее решение уравнения
y′′ − 2y′ + y = 8e3x .
РЕШЕНИЕ. Сначала рассмотрим соответствующее однородное уравнение
y′′ − 2y′ + y = 0.
Так как его характеристическое уравнение λ2 − 2λ +1 = 0 имеет корни
λ1,2 =1, то общее решение однородного уравнения будет иметь вид
y C ex C xex = 1 + 2 .
Теперь найдем частное решение неоднородного уравнения. Правая
часть является произведением числа и показательной функции e3x :

f (x) = 8e3x ⇒ α = 3, β = 0, s = 0.
При этом число α ±βi = 3 не является корнем характеристического урав-
нения. Поэтому частное решение y

неоднородного уравнения надо искать
в виде

y = Ae3x ,
где A – неизвестный коэффициент.
Имеем:

y′′ = 9Ae3x .
Подставим

y′′ в неоднородное уравнение и получим
9Ae3x − 2⋅3Ae3x + Ae3x = 8e3x ,
⇒ 4Ae3x = 8e3x ,
⇒ 4A = 8 или A = 2.
Таким образом,

y = 2e3x – частное решение неоднородного уравне-
ния, а его общее решение имеет вид
( 1 2 )
y = C ex + C xex + 2e3x .

🎬 Видео

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Общее и частное решение дифференциального уравненияСкачать

Линейные неоднородные ДУ с правой частью специального вида | Лекция 11 | Математика: Диффуры | СтримСкачать

Математика без Ху!ни. Линейные неоднородные дифференциальные уравнения 2 порядка.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

1. ЛНДУ с постоянными коэффициентами и правой частью специального вида.Скачать

Линейные неоднородные ДУ 2 порядка с постоянными коэффициентами и правой частью спец вида. Часть 2Скачать

18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

Суперпозиция частных решений линейного неоднородного дифференциального уравненияСкачать

Метод подбора частного решения по правой части дифференциального уравнения #образованиеСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать