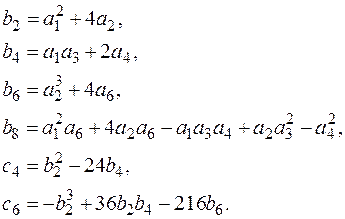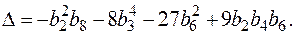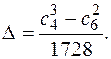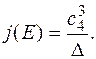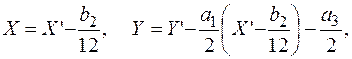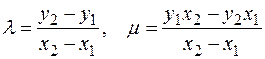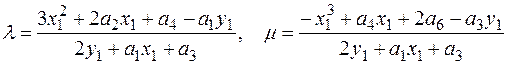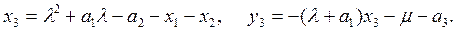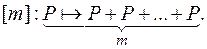Addison-Wesley
Advanced book program
Reading, Massachusetts
LONDON · AMSTERDAM · DON MILLS
ONTARIO · SYDNEY · TOKYO
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1984
 3712 Кб |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эллиптические функции появились в математике в начале XIX века, который из-за обилия открытых в нем различного рода функций математики иногда называют веком специальных функций. Среди всех специальных функций эллиптические функции с момента их открытия выделились универсальностью своих свойств (причем не только аналитического, но и алгебро-арифметического и топологического характера). Именно благодаря разнообразию свойств эллиптические функции постоянно служили источником новых идей и являлись связующим звеном для различных математических теорий.
С историей эллиптических функций и их ролью в математике XIX века читатель может познакомиться по книге «Математика XIX века: геометрия, теория аналитических функций» (под ред. А. Н. Колмогорова и А. П. Юшкевича. М.: Наука, 1981). Здесь же хотелось лишь отметить, что теория эллиптических функций зародилась в трудах Гаусса, Абеля и Якоби. Дальнейшее развитие теории связано с именами Эйзенштейна, Лиувилля, Вейерштрасса, Римана, Кронекера, Фробениуса, Вебера и Фрикке.
В первой половине XX века развивались только отдельные аспекты теории эллиптических функций и в первую очередь те, которые связаны с теорией полей классов. Полученные в этом направлении результаты связаны с именами Гильберта, Фуртвенглера, Тагаки, Е. Артина, Дойринга, Хассе, Шевалле и И. Р. Шафаревича. В полной мере интерес к эллиптическим функциям возродился лишь в последние годы, и этим мы во многом обязаны Шимуре, представившему классические результаты Кронекера, Вебера и Фрикке в совершенно новом свете.
Несмотря на огромный интерес, который вызывали и вызывают эллиптические функции, на русском языке имеется очень мало книг, посвященных собственно эллиптическим функциям. Книга Н. И. Ахиезера «Элементы теории эллиптических функций» (М.: Наука, 1970) затрагивает лишь аналитическую сторону вопроса. В превосходной книге Г. Шимуры «Введение в арифметическую теорию автоморфных функций» (М.: Мир, 1973) эллиптические функции рассмотрены очень сжато, лишь как частный случай общих теорий.
Предлагаемый перевод книги С. Ленга должен в некоторой степени устранить указанный пробел.
Эллиптические функции параметризуют эллиптические кривые и, соединяя в себе аналитические и алгебро-арифметические теории, занимают центральное место в математике с начала XIX столетия.
Недавно в этом старом предмете появились новые технические приемы и точки зрения, продолжающие традиции Кронекера, Вебера, Фрикке, Хассе, Дойринга. Книга Шимуры (Имеется русский перевод: Шимура Г . Введение в арифметическую теорию автоморфных функций. М.: Мир, 1973. Прим. перев. ) является блестящим эталоном современного изложения, и я нашел ее очень полезной для себя при изучении некоторых аспектов эллиптических кривых. Указанная книга придает особое значение ХассеВейля, операторам Гекке и обобщениям на случай высшей размерности (абелевым многообразиям; кривым высших родов, появляющимся из арифметических групп, действующих на верхней полуплоскости; ограниченным симметрическим областям с дискретной арифметической группой, которой является алгебраической).
В предлагаемой книге внимание уделяется некоторым другим аспектам теории. Для ее чтения требуется меньше предварительных знаний, и изложение теории эллиптических функций начинается с самого начала. В книге не обсуждаются операторы Гекке, но рассматриваются некоторые вопросы, не освещенные в книге Шимуры, а именно: теория Дойринга и представлений; приложение к работе Ихары; обсуждение эллиптических кривых с нецелым инвариантом и параметризации Тейта с приложением к работе Серра по группам Галуа точек конечного порядка над числовыми полями и к теореме об изогении; наконец, предельная формула Кронекера и обсуждение значений специальных модулярных функций, являющихся отношениями которые лучше значений функции Вейерштрасса, так как являются единицами при собственной нормализации и ведут себя регулярным образом под действием группы Галуа.
Таким образом, эта книга существенно отличается от книги Шимуры. Однако оказалось невозможным полностью избежать пересечений, и я решил переизложить теорию комплексного умножения, следуя алгебраическому методу Дойринга, а также воспроизвести некоторые результаты Шимуры либо с упрощениями (например, в его законе взаимности для неподвижных точек), либо с другим доказательством (например, для теоремы об автоморфизмах поля модулярных функций).
Я не выделяю особо эллиптические кривые в характеристике p , за исключением случая, когда они возникают при редукции из характеристики 0. Таким образом, я опустил большую часть теории, относящейся к собственно характеристике p , в том числе изящную теорию суперсингулярных инвариантов. Однако хотелось бы предупредить, что эта теория важна для более глубокого понимания арифметической теории эллиптических кривых. Два приложения помогут читателю при ознакомлении с соответствующей литературой.
Видео:Как устроена эллиптическая криптография? Душкин объяснитСкачать
Эллиптические кривые.
Проективная плоскость P 2 (K) над полем K определяется как множество троек (X, Y, Z) не равных одновременно нулю элементов X, Y, Z Î K, на котором введено отношение эквивалентности:
Так, например, две точки (4, 1, 1) и (5, 3, 3) эквивалентны в P 2 (F7).
Класс эквивалентности троек называется проективной точкой.
Эллиптической кривой E называется множество точек проективной плоскости, удовлетворяющих однородному уравнению Вейерштрасса
Это уравнение называют также длинной формой Вейерштрасса. Кривая должна быть неособой в том смысле, что частные производные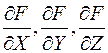 
не должны обращаться в нуль одновременно ни в одной ее точке.
Множество K-рациональных точек кривой E (то есть точек, удовлетворяющих уравнению кривой) обозначается через E(K).
Кривая имеет только одну точку, чья координата Z = 0, а именно (0, 1, 0). Ее принято называть бесконечно удаленной точкой (или точкой на бесконечности) и обозначать символом O.Для удобства часто пользуются аффинной версией уравнения Вейерштрасса:
K-рациональные точки в аффинном случае – это решения уравнения в K 2 и бесконечно удаленная точка O.
Переход от аффинных к проективным координатам:
— точка на бесконечности всегда переходит в бесконечно удаленную точку, как при переходе от аффинных координат к проективным, так и наоборот;
— проективная точка (X, Y, Z) кривой, отличная от бесконечно удаленной (Z ¹ 0), переходит в аффинную точку с координатами (X/Z, Y/Z);
— чтобы найти проективные координаты аффинной точки (X, Y), не лежащей на бесконечности, достаточно выбрать произвольное значение Z Î K * и вычислить (X·Z, Y·Z, Z).
Иногда удобнее пользоваться модифицированной формой проективной плоскости, когда проективные координаты (X, Y, Z) представляют аффинную точку (X/Z 2 , Y/Z 3 ).
Для эллиптической кривой вводятся следующие константы:
Дискриминант кривой E определяется по формуле
Если char K ¹ 2, 3, то дискриминант можно вычислить и так:
Деление на 1728 = 2 6 3 3 имеет смысл только в тех полях, чья характеристика отлична от 2 и от 3. Кривая E неособа тогда и только тогда, когда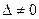 
. Далее рассматриваются только неособые кривые.
Для неособых кривых вводится j-инвариант
он тесно связан с понятием изоморфизма эллиптических кривых.
Говорят, что кривая E с координатами X и Y изоморфна над полем K кривой E’ с координатами X’, Y’ (обе заданы уравнением Вейерштрасса), если найдутся такие константы r, s, t Î K и u Î K * , что при замене переменных
кривая E перейдет в кривую E’. Отметим, что изоморфизм кривых определен относительно поля K. Изоморфизм эллиптических кривых является отношением эквивалентности.
Лемма. Изоморфные над полем K кривые имеют один и тот же j-инвариант. С другой стороны, любые кривые с совпадающими j-инвариантами изоморфны над алгебраическим замыканием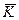 
поля K. То есть j-инвариант разделяет классы эквивалентности отношения изоморфизма над алгебраическим замыканием поля K.
Групповой закон
Рассмотрим для char K ¹ 2, 3 замену переменных
переводящую кривую заданную длинной формой Вейерштрасса в изоморфную ей кривую, определяемую короткой формой Вейерштрасса E: Y 2 = X 3 + aX + b при некоторых a, b Î K. На таких представителях классов изоморфных эллиптических кривых можно наглядно ввести групповой закон методом хорд и касательных.
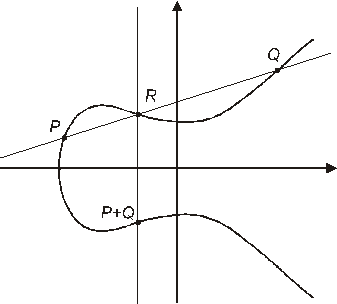
Сложение точек определяется с помощью хорд. Пусть P и Q – две точи кривой. Соединим их прямой линией. Она обязательно пересечет кривую в какой-то третьей точке R поскольку мы пересекаем кубическую кривую прямой. Точка R будет определена над тем же полем, что сама кривая и исходные точки P и Q. Отразим затем точку R относительно горизонтальной оси координат и получим точку, определяемую над основным полем. Последняя точка и будет суммой P + Q.
Рис.38. Групповой закон. Сложение точек.
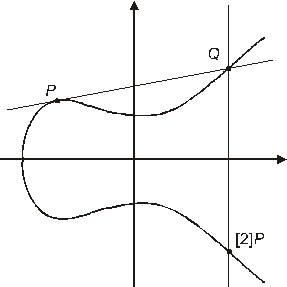
Касательные служат для удвоения точек (используя хорду нельзя сложить точку с собой). Пусть P – произвольная точка эллиптической кривой. Проведем касательную к кривой в точке P. Она пересечет кривую в какой-то третьей точке R (кубическая кривая пересекается по трем точкам с учетом кратности пересечения). Отразив R относительно горизонтальной оси, мы получим точку [2]P = P + P. Вертикальная касательная в точке P «пересекает» кривую в бесконечно удаленной точке. В этой ситуации P + P = O и говорят, что P – точка порядка 2.
Рис.39. Групповой закон. Удвоение точек.
Метод хорд и касательных наделяет эллиптическую кривую структурой абелевой группы с бесконечно удаленной точкой в качестве нейтрального (единичного) элемента, то есть нуля. Определение операций можно легко перенести на случай общей эллиптической кривой, заданной длинной формой Вейерштрасса (в частности характеристика поля может быть любой). Необходимо только заменить отражение относительно оси абсцисс на симметрию относительно прямой
Алгебраические формулы, реализующие сложение точек по методу хорд и касательных.
Лемма. Пусть E – эллиптическая кривая, определяемая уравнением
Фиксируем натуральное число m и обозначим через [m] отображение кривой на себя, сопоставляющее каждой точке P ее кратное [m]P, то есть
Это отображение – основа криптографических систем, опирающихся на эллиптическую кривую, поскольку его можно легко вычислить, но крайне сложно обратить, то есть по данным координатам P(x, y) и [m]P(x’, y’) найти m очень трудно. (Конечно сложность обращения предполагает специальный выбор эллиптической кривой и соблюдения других условий).
Дата добавления: 2016-02-13 ; просмотров: 2895 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Занятие 31. Группа точек на эллиптической кривой. Криптосистема Диффи-Хеллмана на ЭКСкачать
dxdt.ru: занимательный интернет-журнал
Видео:ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ «НА ПАЛЬЦАХ»Скачать
Книги: «Создание сайтов» — «Доменные войны». Защита информации: техническое описание TLS, тестовый сервер TLS 1.3. Ресурсы: LaTeX
Видео:Алгоритм цифровой подписи на основе эллиптической кривой ECDSA: Как он защищает ваш биткоин-кошелек?Скачать
Фрукты и эллиптические кривые
Многие слышали про криптографию на эллиптических кривых. Но эллиптические кривые, которые давно являются мощным инструментом теории чисел, можно успешно применить к решению элементарной (по формулировке) арифметической задачки про бананы, яблоки и ананасы. Текст ниже – несколько сокращённая версия моего перевода ответа Quora.com, который дал Alon Amit (англ.).
В Сети нередко можно натолкнуться на различные задачи, сформулированные при помощи картинок, которые содержат какую-нибудь “арифметику” с фруктами (или другими объектами быта) и утверждения типа “Только 5% людей могут решить это”. Обычно, задачи довольно бестолковые, служащие для привлечения внимания к каким-нибудь онлайн-тестам.
(Найдите решение в целых положительных значениях для яблока, банана и ананаса.)
Однако эта задача только выглядит простой. Её можно решить (ниже мы разберём как), но решение оказывается сложным и требует специальных математических знаний. Может показаться, что если не удалось найти “формулы” для решения, то, так как это вроде бы простое уравнение и маленькое число 4, можно вооружиться практически любым языком программирования и поручить компьютеру перебор. Компьютеры нынче быстрые, поэтому ответ, возможно, найдётся практически тут же. Но это далеко не так. Грубый компьютерный перебор здесь просто оказывается бесполезен.
Перепишем задачу в привычных обозначениях. Мы хотим найти решения в целых положительных числах уравнения:
Прежде всего хорошо бы понять, к какому типу уравнений относится данное. Здесь требуется найти решения в целых числах (даже в натуральных). Похоже, это задача из области теории чисел. Выражение записано в рациональных функциях, но, домножив на общее кратное, можно легко получить многочлен, представляющий собой диофантово уравнение (диофантовыми называют уравнения с целыми коэффициентами, решения которых также ищут в целых или натуральных числах; пример диофанового уравнения: x^5 + y^5 = z^5 – АВ). Поиск решений в целых положительных числах делает задачу существенно более трудной, как мы убедимся ниже.
Сколько у нас переменных? На первый взгляд – три: a, b и c. Но намётанный глаз сразу обратит внимание на то, что уравнение однородное (степени всех одночленов, или мономов, равны – АВ). Поэтому, если (a, b, c) – решение, то и тройка (7a, 7b, 7c) – тоже решение. Любая такая кратная тройка будет решением, число 7 здесь взято только для примера. Умножение всех переменных на константу ничего не изменяет, так как константа сокращается:
Уравнение только кажется трёхмерным, на самом деле – оно двумерное. Геометрически, это двумерная поверхность. Именно такая поверхность определяется единственным уравнением с тремя переменными, например, x^2 = y + z^2 . Более того, наша поверхность получается движением образующей линии, то есть, понять свойства поверхности можно при помощи изучения её сечения плоскостью. Такое сечение оказывается проективной кривой (грубо говоря, алгебраической кривой с присоединённой бесконечно удалённой точкой – АВ).
Данное наблюдение означает следующее. У нас есть тройки (кортежи) решений. Мы можем разбить все решения на классы, в соответствии со значением (например) переменной c: с = 0 и c ≠ 0. Первый класс решений (c = 0) фактически использует только две переменных: a и b. Решения из второго класса мы можем разделить на c и получить вариант с фиксированным значением c = 1. То есть, мы можем искать рациональные решения, где c = 1, а потом получить целые решения (a, b, c), умножив значения на общее кратное. То есть, целочисленные решения однородного уравнения соответствуют рациональным решениям некоторого неоднородного уравнения, размерность (число переменных) которого на единицу меньше.
Какова степень нашего уравнения? Степенью уравнения (многочлена) называют максимальную степень монома (то есть, элементарной части многочлена), которая определяется как сумма степеней входящих в него переменных. Например, степень a 2 bc 4 равна 7, так как 7 = 2 + 1 + 4 .
Свойства диофантовых уравнений существенно различаются в зависимости от степени:
- уравнения степени 1 – очень лёгкие;
- степени 2 – полностью изучены, и обычно поддаются простейшим методам;
- степени 3 – это огромный, глубоко теоретический, океан и куча нерешённых проблем;
- диофантовы уравнения степеней 4 и выше – очень и очень сложная область.
Наше уравнение имеет степень 3. В этом легко убедиться, умножив на общее кратное:
a(a + b)(a + c) + b(b + a)(b + c) + c(c + a)(c + b) = 4(a + b)(a + c)(b + c)
Не нужно раскрывать все скобки, чтобы увидеть, как получается третья степень: никакую из переменных не придётся умножать на саму себя более двух раз. У нас будут получаться a 3 , b 2 c и abc, но суммарная степень не превысит 3. Раскрыв скобки и упростив, получим следующее уравнение:
a 3 + b 3 + c 3 – 3(a 2 b + ab 2 + a 2 c + ac 2 + b 2 c + bc 2 ) – 5abc = 0
Вы можете возразить, что нельзя умножать на знаменатели, так как какой-то из них может быть равен нулю. Действительно, наше новое уравнение имеет несколько решений, которые не соответствуют исходному. Но так даже лучше. Дело в том, что такое преобразование улучшает ситуацию, упрощая работу с уравнением. Просто, если мы найдём какое-то решение, потребуется проверить, что оно не делает никакой из исходных знаменателей равным нулю.
Нетрудно найти корень нового уравнения. Например: a = -1, b = 1, c = 0 – рациональное решение, или рациональная точка. Это подсказывает, что наше кубическое уравнение на самом деле эллиптическая кривая.
Первое, что нужно сделать с уравнением эллиптической кривой, это привести его к форме Вейерштрасса:
y 2 = x 3 + ax + b
или (полная форма):
y 2 =x 3 + ax 2 + bx + c
К форме Вейерштрасса можно привести всякое уравнение эллиптической кривой (исключения относятся к случаю полей малой характеристики, но нас этот момент сейчас не касается). Процесс преобразования существенным образом использует тот факт, что известна по крайней мере одна рациональная точка, и обычно оказывается трудоёмким, но это всего лишь механический процесс, который, к тому же, автоматически выполняют некоторые системы компьютерной алгебры. В нашем случае результат преобразования представляет собой пару пугающих формул:
Как только появились эти формулы, можно, путём пусть и утомительных, но очевидных алгебраических преобразований, получить следующее уравнение:
y 2 = x 3 + 109x 2 + 224x (2)
Это уравнение выглядит совсем иначе, но, тем не менее, является верной моделью оригинального. Его график представлен ниже – типичная эллиптическая кривая с двумя вещественными компонентами.
Ласточкин хвост справа растёт до бесконечности и дальше. А замкнутая овальная часть слева – и есть самое интересное для нас место.
Решение (x,y) данного уравнения позволяет получить решение (a,b,c) исходного:
Отображения, которые мы построили из (a,b,c) в (x,y) и обратно, показывают, что два уравнения являются “одинаковыми” с точки зрения теории чисел: рациональные решения одного уравнения дают рациональные решения другого, то есть, между ними установлена бирациональная эквивалентность. Понятие бирациональной эквивалентности – одно из фундаментальных в алгебраической геометрии. Как отмечено выше, в нашем случае есть некоторые “исключительные” точки, а именно, те, в которых (a+b),(a+c) или (b+c) равны нулю. Обычное дело в бирациональной геометрии, но нам это никаких проблем не доставит.
Рассмотрим пример. Эллиптическая кривая (2) содержит привлекательную рациональную точку: x=-100, y=260. Найти её не так легко, как проверить, что значения – верные. Просто подставьте числа в уравнение и убедитесь, что обе части равны. Теперь мы можем проверить и значения a, b, c, соответствующие данной точке:
Мы можем умножить на общее кратное, что даст целые числа:
Подставляем в исходную задачу. Всё сходится:
Числа, составляющие этот ответ, целые, но не все они положительные, поэтому не подходят к исходной задаче. Нашу тройку чисел не так легко определить умозрительно, но, тем не менее, вполне реально подобрать вручную, не используя компьютер. Так что обещанная трудность задачи кроется в требовании решения в натуральных числах.
Как только у нас есть рациональная точка на кривой (2), мы можем получить другие рациональные точки, используя метод секущих и касательных для сложения точек. Начнём с точки P=(-100,260) и сложим её с самой собой. Это делается при помощи нахождения точки пересечения кривой и касательной к ней, проведённой в точке P. При этом, для определения суммы, точку нужно отразить относительно горизонтальной оси. (Принципы метода секущих и касательных показаны на рисунках ниже.)
(Удвоение точки.)
(Сложение двух точек.)
Результат удвоения точки P выглядит несколько более пугающим:
P + P = 2P = (8836/25, -950716/125)
Эта новая точка соответствует значениям a, b, c, которые так же походят к исходному уравнению:
(a, b, c) = (9499, -8784, 5165)
Можно с уверенностью сказать, что это решение непросто найти перебором вручную, но вполне реально при помощи простейшей программы на компьютере. Как бы там ни было, оно всё ещё не удовлетворяет требованию положительности.
Продолжим складывать точки и вычислим 3P=2P+P, соединив 2P и P прямой (секущей) и найдя пересечение с кривой. Снова определим a, b, c, и убедимся, что не все значения положительные. То же будет для 4P, 5P и так далее… пока мы не попадём в точку 9P.
Эту точку совершенно точно нелегко было бы найти, но всё что потребовалось сделать при помощи нашего метода – это несколько раз применить простой геометрический алгоритм. Соответствующие значения a, b, c удивительны:
a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036
Это 80-значные числа. На практике невозможно найти 80-значные решения исходной задачи простым перебором на компьютере – это займёт слишком много времени. Удивительно, но при подстановке в наше исходное уравнение a/(b+c)+b/(a+c)+c/(a+b) найденные числа дают результат ровно 4. Оказывается, это наименьшее решение задачи. По мере того, как мы складываем точку P с самой собой, знаменатели уравнения продолжают расти. Доказать это не так просто, однако теория высот на эллиптических кривых позволяет показать, что эти астрономические числа, действительно, наименьшее решение исходной задачи.
Уже 80-значные числа в ответе – велики. Но если вместо 4 подставить 178, то для записи чисел решения потребуется 398605460 десятичных цифр. Нет, это не один из ответов, это лишь число знаков, которые потребуются, чтобы его записать. А для значения 896 запись решения потребует триллионы знаков.
Это впечатляющий пример того, что у диофантовых уравнений с маленькими коэффициентами могут быть огромные решения.
📹 Видео
Занятие 30. Эллиптические шифры, их преимущество. Эллиптическая кривая с примером построения.Скачать
Эллиптическая криптография - Денис КовалевСкачать
Введение в эллиптическую криптографиюСкачать
Эллиптические кривые. Сложение точек. Автор - @aimemiaСкачать
Что такое эллиптические кривые и зачем они нужны?Скачать
Crypto bits #4 | ECC (криптография эллиптической кривой), ECDSA и использование в EthereumСкачать
#elliptic cylinder#Elliptic cone#shorts #maths #youtubeshorts #viralСкачать
ВОКРУГ ЭЛЛИПТИЧЕСКИХ КРИВЫХ — ВАДИМ ВОЛОГОДСКИЙСкачать
2020.12.03.Свойства эллиптических кривыхСкачать
В.А. Клепцын. ℘-функция Вейерштрасса, ряды Эйзенштейна и модулярные функции. Семинар 1Скачать
2020.11.26.Классы стойкости. Определение эллиптической кривойСкачать
В.А. Клепцын. ℘-функция Вейерштрасса, ряды Эйзенштейна и модулярные функции. Семинар 3Скачать
Эллиптические кривые и функциональные уравнения. Елена Нетай.Скачать
В.А. Клепцын. ℘-функция Вейерштрасса, ряды Эйзенштейна и модулярные функции. Семинар 2Скачать
Finding points satisfying Elliptic Curve equationСкачать
§31.1 Приведение уравнения кривой к каноническому видуСкачать
