Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 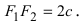
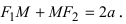
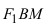
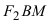
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 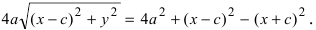
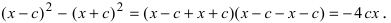
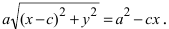
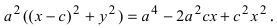
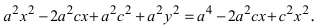
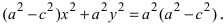
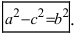
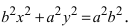
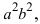
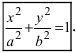
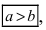
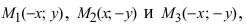
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
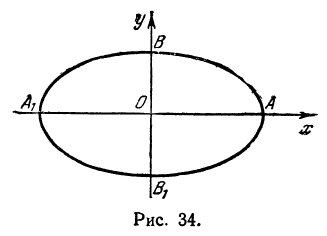
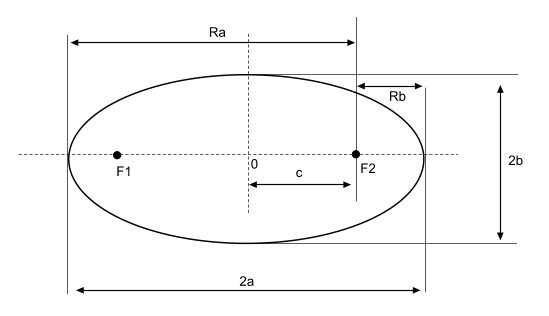
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 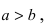
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 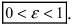
Если 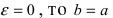
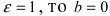
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 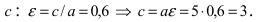
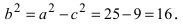
Пример:
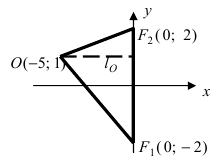
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 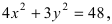
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
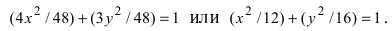
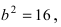
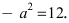
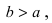
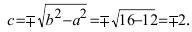
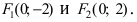
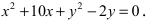
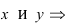
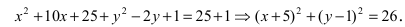
Построим в декартовой системе координат треугольник 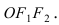
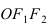
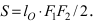
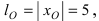
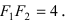
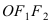
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Эллипс в высшей математике
где 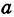
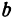
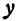
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
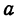

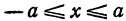
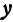
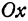
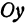
При 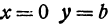
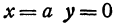
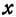

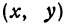
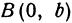
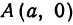
Полученная линия называется эллипсом. Число 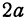
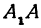
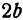
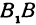
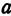
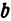
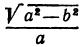
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
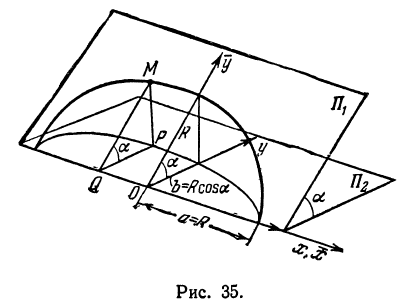
Возьмем две плоскости, пересекающиеся под углом 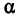
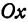
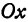
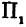
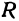
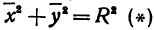
Пусть точка 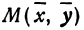
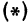
Обозначим проекцию точки 
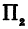
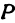
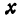
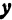


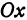
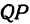
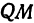
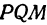
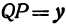
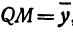
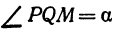
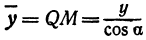


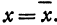
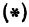
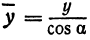
а это есть уравнение эллипса с полуосями 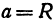
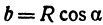
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 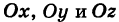
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 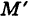
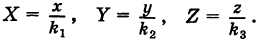
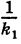
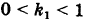
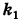
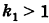
Подставляя эти формулы в уравнение (1), будем иметь
где 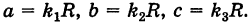
Величины 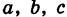
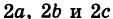
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
| Первая координата |
| Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей — большая полуось и малая полуось ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)
Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия — отношение длин малой и большой полуосей
Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса | |||
| Большая полуось эллипса | |||
| Малая полуось эллипса | |||
| Эксцентриситет эллипса | |||
| Фокусное/фокальное расстояние | |||
| Коэффициент сжатия | |||
| Координаты первого фокуса F1(x1:y1) | |||
| Координаты второго фокуса F2(x2:y2) | |||
| Фокальный параметр | |||
| Перифокусное расстояние | |||
| Апофокусное расстояние | |||
И еще один пример Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса. Если мы введем данные в калькулятор получим
|
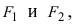
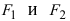
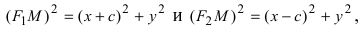
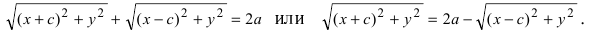
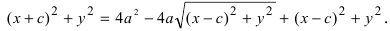
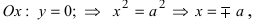 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 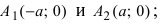
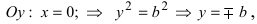 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 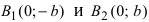 (Рис. 30).
(Рис. 30).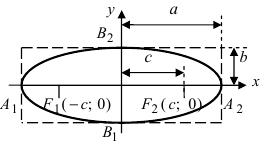
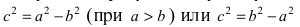
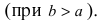
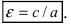
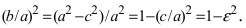
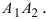
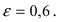
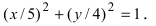
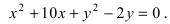
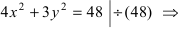
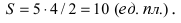

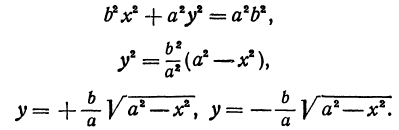
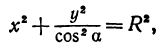
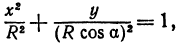

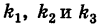
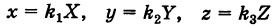
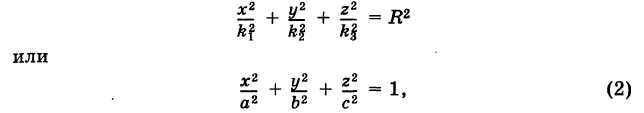




 . При a = b эллипс превращается в окружность, уравнение эллипса (2.17) принимает вид : x 2 + y 2 = a 2 . Отношение
. При a = b эллипс превращается в окружность, уравнение эллипса (2.17) принимает вид : x 2 + y 2 = a 2 . Отношение  половины расстояния между фокусами к большой полуоси эллипса – эксцентриситет эллипса
половины расстояния между фокусами к большой полуоси эллипса – эксцентриситет эллипса  . Причем 0 ε 1, так как 0 c a .
. Причем 0 ε 1, так как 0 c a .
 – директрисы эллипса.
– директрисы эллипса. есть величина постоянная, равная эксцентриситету эллипса:
есть величина постоянная, равная эксцентриситету эллипса:  .
. . Данный эллипс будет растянут вдоль оси 0 y .
. Данный эллипс будет растянут вдоль оси 0 y . .
. между двумя точками получаем:
между двумя точками получаем:



 . Проведя преобразования, аналогичные упрощениям уравнения эллипса, получим каноническое уравнение гиперболы:
. Проведя преобразования, аналогичные упрощениям уравнения эллипса, получим каноническое уравнение гиперболы: . Это означает, что точки гиперболы расположены справа от прямой x = a (правая ветвь гиперболы) и слева от прямой x =– a (левая ветвь) (рис. 2.6).
. Это означает, что точки гиперболы расположены справа от прямой x = a (правая ветвь гиперболы) и слева от прямой x =– a (левая ветвь) (рис. 2.6).
 – сохраняет значение, равно e единице. Следовательно, гипербола имеет форму, состоящую из двух неограниченных ветвей.
– сохраняет значение, равно e единице. Следовательно, гипербола имеет форму, состоящую из двух неограниченных ветвей. имеет две асимптоты:
имеет две асимптоты:  . Так как данные прямые и гипербола (2.18) симметричны относительно координатных осей, то достаточно рассмотреть только точки, расположенные в первой четверти.
. Так как данные прямые и гипербола (2.18) симметричны относительно координатных осей, то достаточно рассмотреть только точки, расположенные в первой четверти. точку N , имеющую ту же абсциссу, что и точка M ( x ; y ) на гиперболе
точку N , имеющую ту же абсциссу, что и точка M ( x ; y ) на гиперболе  . Найдем разность | MN | :
. Найдем разность | MN | :
 – есть асимптоты гиперболы (рис. 2.7).
– есть асимптоты гиперболы (рис. 2.7).
 . Так как у гиперболы c > a , то эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как
. Так как у гиперболы c > a , то эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как  . Видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение
. Видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение  ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
ее полуосей, а значит, тем более вытянут ее основной прямоугольник. . Действительно,
. Действительно,  . Фокальные радиусы , для точек правой ветви гиперболы имеют вид: r 1 = εx + a , r 2 = εx – a ; для точек левой ветви: r 1 =–( εx + a ), r 2 =–( εx – a ) .
. Фокальные радиусы , для точек правой ветви гиперболы имеют вид: r 1 = εx + a , r 2 = εx – a ; для точек левой ветви: r 1 =–( εx + a ), r 2 =–( εx – a ) . называются директрисами гиперболы. Тот факт, что для гиперболы ε > 1, то
называются директрисами гиперболы. Тот факт, что для гиперболы ε > 1, то  означает : правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной. Директрисы гиперболы имеют тоже свойство
означает : правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной. Директрисы гиперболы имеют тоже свойство  , что и директрисы эллипса.
, что и директрисы эллипса. определяет гиперболу с действительной осью 2 b , расположенной на оси 0 y , и мнимой осью 2 a, расположенной на оси абсцисс (подобная гипербола изображена на рисунке 2.7 пунктиром).
определяет гиперболу с действительной осью 2 b , расположенной на оси 0 y , и мнимой осью 2 a, расположенной на оси абсцисс (подобная гипербола изображена на рисунке 2.7 пунктиром). и имеют общие асимптоты. Такие гиперболы называются сопряженными.
и имеют общие асимптоты. Такие гиперболы называются сопряженными.














