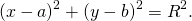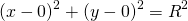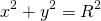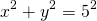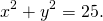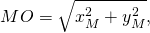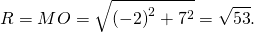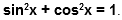Чем окружность с центром в начале координат отличается от других окружностей?
Окружность с центром в точке (a;b) и радиусом R задаётся уравнением
Для окружности с центром в начале координат a=0, b=0:
Таким образом, уравнение окружности с центром в начале координат имеет вид
1) Написать уравнение окружности с центром в начале координат и радиусом 5.
В формулу уравнения окружности с центром в начале координат подставляем R=5:
2) Составить уравнение окружности с центром в начале координат, проходящей через точку M(-2;7).
Теперь запишем уравнение окружности с центром в точке O(0;0) и R=√53:
Видео:Уравнение окружности (1)Скачать
Уравнение единичной окружности с центром в начале координат
Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать
Окружность с центром в начале координат
Чем окружность с центром в начале координат отличается от других окружностей?
Окружность с центром в точке (a;b) и радиусом R задаётся уравнением
Для окружности с центром в начале координат a=0, b=0:
Таким образом, уравнение окружности с центром в начале координат имеет вид
1) Написать уравнение окружности с центром в начале координат и радиусом 5.
В формулу уравнения окружности с центром в начале координат подставляем R=5:
2) Составить уравнение окружности с центром в начале координат, проходящей через точку M(-2;7).
Теперь запишем уравнение окружности с центром в точке O(0;0) и R=√53:
Видео:10 класс, 11 урок, Числовая окружностьСкачать
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:9 класс, 6 урок, Уравнение окружностиСкачать
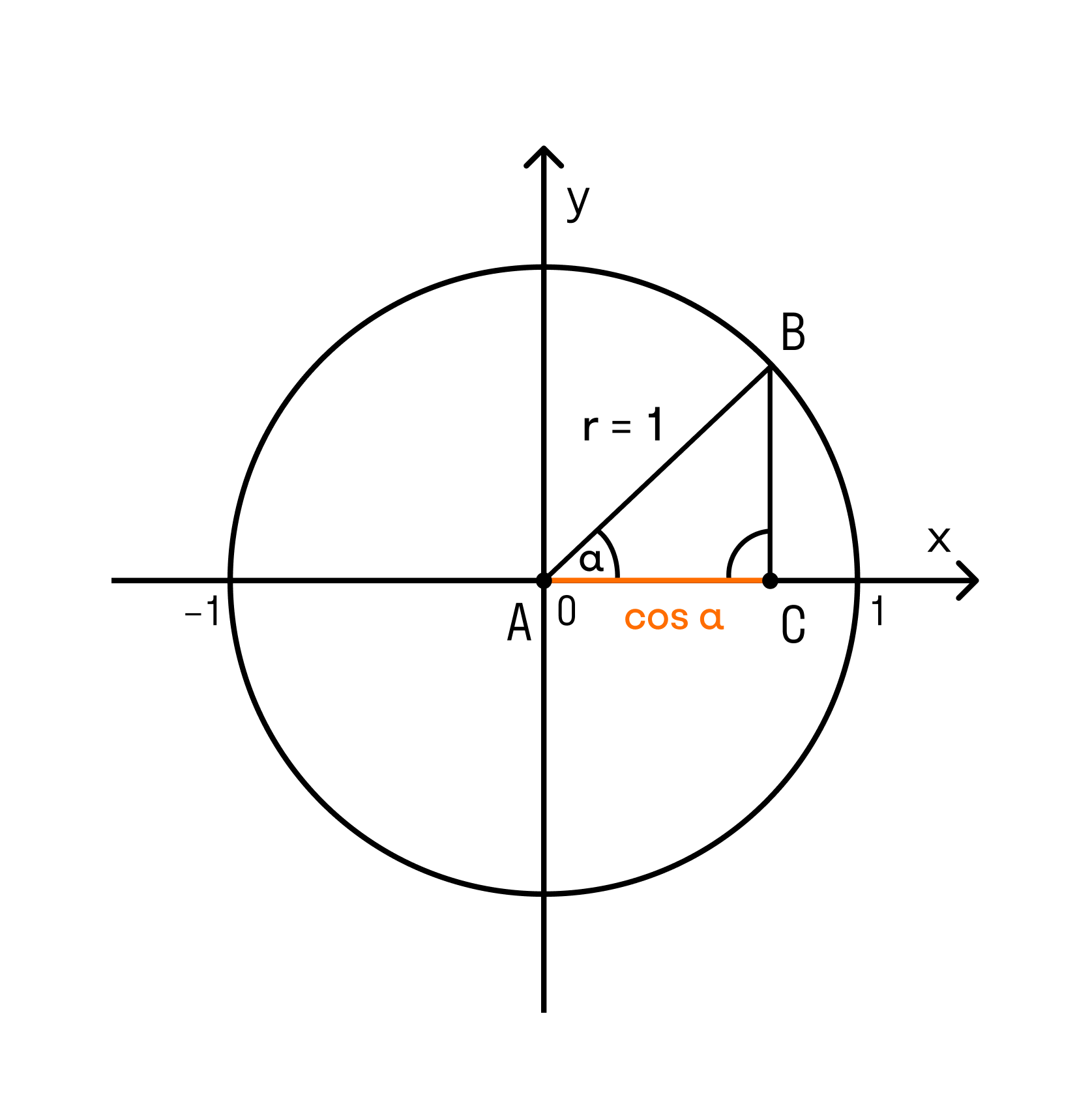
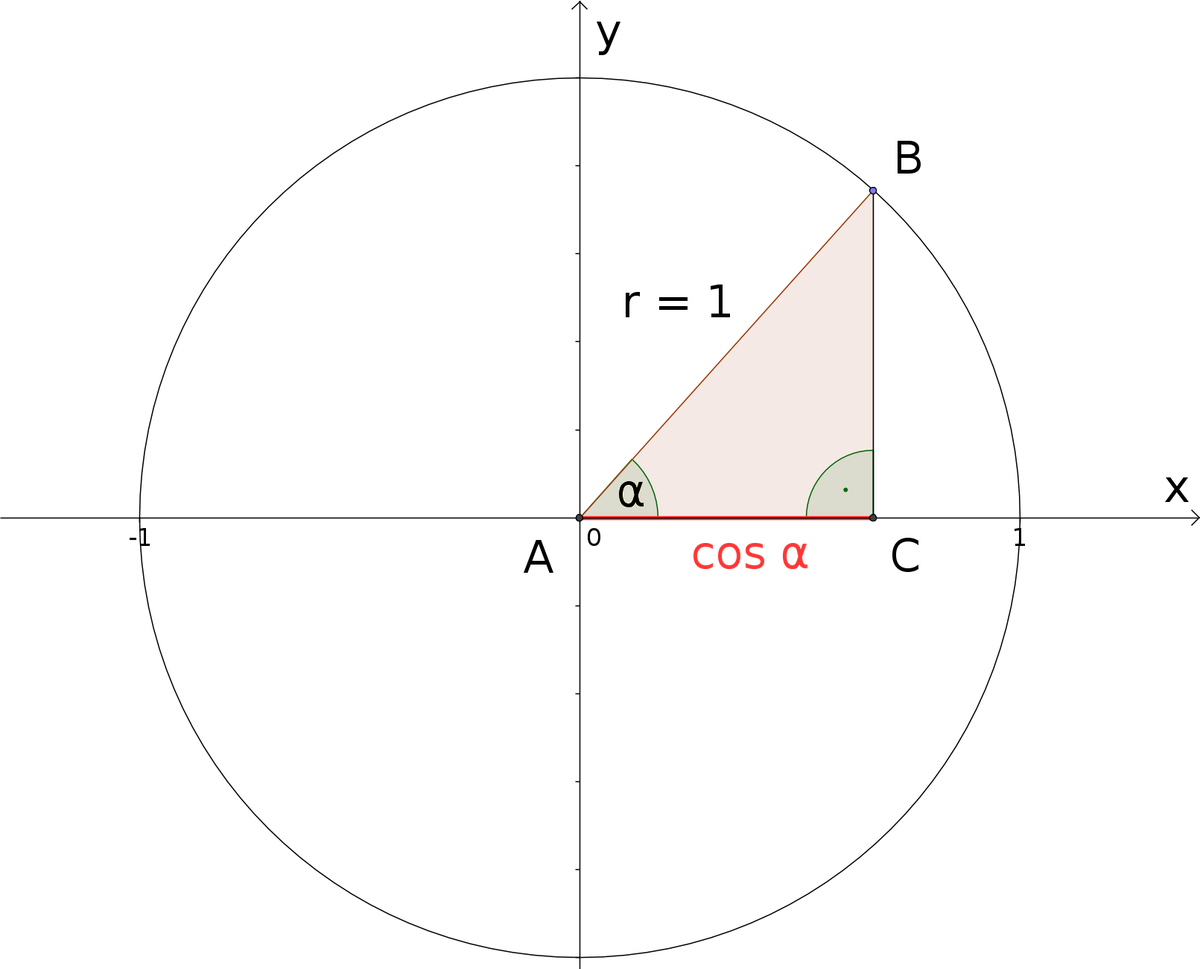
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать
Единичная окружность: определение, связь с тригонометрией
Единичная окружность — это окружность с радиусом, равным единице, и центром в начале прямоугольной декартовой системы координат.
Уравнения для задания единичной окружности: x 2 + y 2 = 1
Понятие единичной окружности непосредственно связано с тригонометрией. Угол поворота можно рассматривать, как движение по окружности. При этом величина угла поворота не зависит от радиуса окружности, что делает использование единичной окружности при математических описаниях очень удобным.
Через координаты точек на единичной окружности дается определение основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Обосновываются их свойства и выводятся основные формулы тригонометрии.
С использованием уравнения единичной окружности и определения синуса и косинуса может быть записано основное тригонометрическое тождество: sin 2 x + cos 2 x = 1 .
Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать
Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
📹 Видео
ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать
Тригонометрическая окружность. Как выучить?Скачать
🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать
Как найти координаты точек на тригонометрической окружностиСкачать
Как искать точки на тригонометрической окружности.Скачать
Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать
№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать
№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать
УРАВНЕНИЕ ОКРУЖНОСТИСкачать
Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать
Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать
ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬСкачать
начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать
