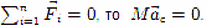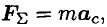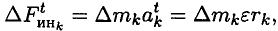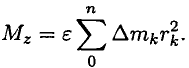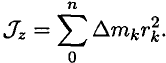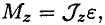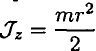Уравнение движения системы материальных точек

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Система материальных точек. Вывод уравнения движения системы материальных точек на примере двух жестко связанных тел(хз)

Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы. Часто систему материальных точек называют механической системой.

Центр масс системы материальных точек. Определение радиус-вектора центра масс. Свойства центра масс. Скорость центра масс. Вывод уравнения движения центра масс. Закон сохранения координаты центра масс системы материальных точек.

тром масс (или центром инерции)

системы материальных точек называет-

ся воображаемая точка С, положение

которой характеризует распределение

массы этой системы. Ее радиус-вектор

Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.

Скорсть центра масс

Для непрерывного распределения массы с плотностью r . Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если не параллельны, то центр масс и центр тяжести не совпадают.
Взяв производную по времени от , получим:

т.е. полный импульс системы равен произведению ее массы на скорость центра масс.

Подставляя это выражение в закон изменения полного импульса, находим:

Центр масс системы движется как частица, в которой сосредоточена вся масса системы и к которой приложена результирующая внешних сил.

При поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс.

Так как , то центр масс замкнутой системыдолжен сохранять состояние покоя или равномерного прямолинейного движения, т.е. =const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.

Rс(t1) = Rc(t2) закон сохранения координаты центра масс

Работа потенциальных (консервативных) силы на примере силы тяжести. Определение потенциальных (консервативных) силовых полей. Введение понятия потенциальной энергии через работу силы. Связь силы и потенциальной энергии

Потенциальная сила — сила, работа к-рой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки. Консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Потенциальное (консервативное) силовое поле:Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.
Введения понятия потенц. Энергии через работу сил — Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля.
Связь силы и потенциальной энергии — Каждой точке потенциального поля соответствует некоторое значение силы , действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой и U должна быть связь , с другой стороны, dA = –dU,

Видео:Система материальных точек. Центр масс. Закон движения центра масс. Видеоурок по физике 10 классСкачать

Система материальных точек. Уравнение поступательного движения системы материальных точек. Центр инерции

Совокупность тел, рассматриваемых как единое целое, называют механической системой.

Силы, с которыми взаимодействуют материальные точки системы между собой, называют внутренними силами. Силы, с которыми на материальные точки системы действуют тела, не входящие в данную систему (внешние тела), называют внешними силами.

Механическая система тел, на которую не действуют внешние силы, называется замкнутой, или изолированной, системой.

Для простоты рассуждений рассмотрим вначале систему, состоящую из двух материальных точек с массами и , которые расположены на оси абсцисс в точках с координатами и (рис. 1). Расстояние между этими точками . Точку С, которая делит это расстояние на отрезки, обратно пропорциональные массам, называют центром масс.

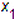
Следовательно, по определению

(1)

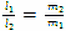
Пусть координата этой точки тогда . Подставим в уравнение (1), .

(2)

Формула (2) позволяет определить координату центра масс системы, состоящей из двух материальных точек.

Выражение (2) можно обобщить на систему n материальных точек, расположенных произвольным образом. Координата центра масс

(3)

Аналогичные выражения получаются и для координат и .

Положение центра масс можно также определить с помощью радиуса-вектора:

,

где и — масса и радиус-вектор i-й частицы.

При движении материальных точек системы координаты их изменяются. Записав выражение (3) для двух моментов времени и , вычтем одно из другого и получим:

Разделив обе части этого выражения на промежуток времени , имеем:

где — проекции на ось Ox векторов скорости движения центра масс и материальных точек 1, 2 . n.

Аналогичные выражения можно записать и для проекции скорости на оси Оу и Oz.

Выражение для нахождения скорости движения центра масс в векторном виде:

(4)

При движении материальных точек системы центр масс перемещается. Определим, от чего зависит характер движения центра масс.

Для этого рассмотрим систему двух материальных точек. Пусть на эти материальные точки действуют внешние силы и и эти точки взаимодействуют между собой силами (рис. 2).

Запишем для каждой материальной точки второй закон Ньютона:

Выразим ускорение точек через их начальные и конечные скорости:

Подставим полученные выражения во второй закон Ньютона:

Складывая эти равенства, имеем:

(5)

Поскольку по третьему закону Ньютона . Из формулы (4) получаем:

где — скорости движения центра масс в начальный момент времени и через промежуток времени . Тогда равенство (5) можно записать так:

(6)

Выражение (6) показывает, что изменить скорость движения центра масс системы материальных точек могут только внешние силы, внутренние силы изменяют скорости движения отдельных материальных точек.

Обозначим — суммарная масса материальных точек системы. Следовательно,

(7)

т. е. центр масс системы движется как материальная точка в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Выражение (7) представляет собой закон движения центра масс.

Если система материальных точек замкнутая, т. е.

Следовательно, центр масс замкнутой системы материальных точек движется равномерно и прямолинейно либо остается неподвижным независимо от того, как движутся отдельные материальные точки системы.

Так, если в инерциальной системе отсчета центр масс замкнутой системы был неподвижен в какой-то момент времени, то он будет оставаться в покое, несмотря на движение отдельных материальных точек системы в результате их взаимодействия.

Таким образом, центр масс (центр инерции) системы, положение которого характеризует распределение масс этой системы и определяется формулой (3), а скорость которого определяется формулой (4), является характерной точкой для системы, поведение которой подчиняется законам Ньютона и не зависит от природы сил взаимодействия в системе.

Понятие центра масс относится и к одиночному телу, которое можно представить как совокупность материальных точек. Центр масс тела можно рассматривать как точку (находящуюся внутри тела или вне его), в которой пересекаются линии действия сил, приводящих данное тело в поступательное движение. Центр масс тела совпадает с его центром тяжести.

Видео:Дифференциальные уравнения движения точкиСкачать

Основы динамики системы материальных точек

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Основы динамики системы материальных точек

Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.

Любое материальное тело в механике рассматривается как механическая система, образуемая совокупностью материальных точек.

Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения остальных точек.

Силы, действующие на точки системы, делятся на внешние и внутренние. Силы взаимодействия между точками этой системы называют внутренними. К внешним силам относятся силы, действующие со стороны точек, не входящих в эту систему.

Примерами внешних сил являются сила тяжести, сила давления, сила трения и др.

К внутренним силам относятся силы упругости.

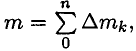
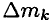
Движение механической системы зависит не только от внешних сил, но и от суммарной массы системы где — масса отдельных точек механической системы.

Движение системы зависит и от положения центра масс ей стемы — условной точки, в которой сосредоточена вся масса тела. Обычно считают, что в центре масс приложены все внешние силы.

Движение центра масс определяет движение всей системы толь ко при поступательном движении, при котором все точки тела дви жутся одинаково.

Основное уравнение динамики при поступательном движении тела

Для определения движения тела (системы материальных точек можно использовать второй закон динамики

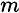
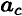
где — суммарная масса тела; — ускорение центра масс тела.

В поле земного притяжения центр масс совпадает с центров тяжести.

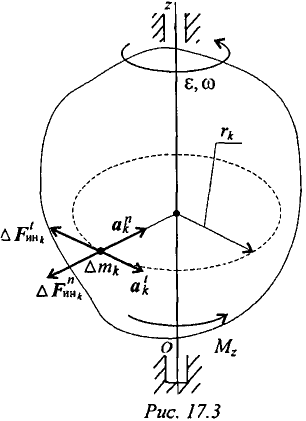
Основное уравнение динамики вращающегося тела

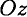
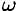
Пусть твердое тело под действием внешних сил вращается вокруг оси с угловой скоростью (рис. 17.3).

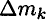
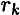
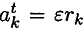
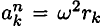
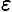
Рассматривая твердое тело как механическую систему, разобьем ее на множество материальных точек с массами . Каждая точка движется по окружности радиуса с касательным ускорением и нормальным ускорением где — угловое ускорение.

Используем для каждой точки принцип Даламбера и приложим силы инерции:

— касательную ;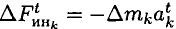

— нормальную .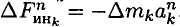

Система сил, действующих на точку, по принципу Даламбера, находится в равновесии.

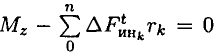
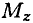
Поэтому алгебраическая сумма моментов относительно оси вращения должна быть равна нулю: , где — момент внешних сил.

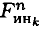
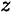
Моменты нормальных сил инерции равны нулю, т. к. силы пересекают ось . Силы, направленные по касательной к окружности, равны

где 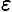— общая величина, угловое ускорение тела.

Подставив значение силы в формулу для определения моментов, получим

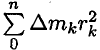
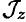
Величина называется моментом инерции тела относительно оси вращения и обозначается .

В результате получим выражение основного уравнения динамики вращающего тела:

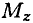
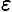
где — сумма моментов внешних сил относительно оси; — угловое ускорение тела.

Момент инерции тела в этом выражении определяет меру инертности тела при вращении.

По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ .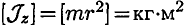

Видно, что значение момента инерции зависит от распределения массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от оси вращения. Для увеличения момента инерции используют колеса со спицами и отверстиями.

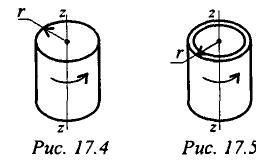
Моменты инерции некоторых тел

Момент инерции сплошного цилиндра (рис. 17.4)

Момент инерции полого тонкостенного цилиндра (рис. 17.5) .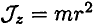

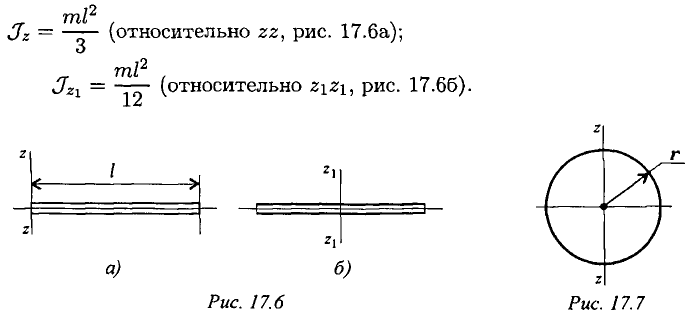
Момент инерции прямого тонкого стержня любого поперечного сечения

Момент инерции шара (рис. 17.7)

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🔥 Видео

Дифференциальные уравнения движения материальной точкиСкачать

Дифференциальное уравнение движения материальной точки.Скачать

Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Д1 Дифференциальные уравнения движения материальной точкиСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Уравнение движенияСкачать

Динамика системы материальных точек | Общая физика. Механика | Евгений БутиковСкачать

Консультация к устному экзамену. Механика. Часть 1: "Движение материальной точки"Скачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Задача на движение материальной точки - bezbotvyСкачать

3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Дифференциальные уравнения движения материальной точки. Часть 1Скачать