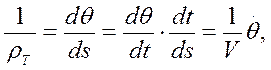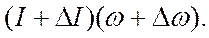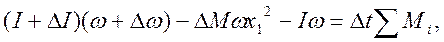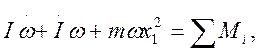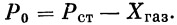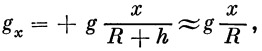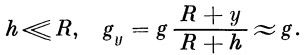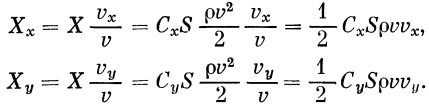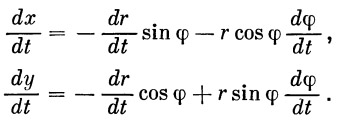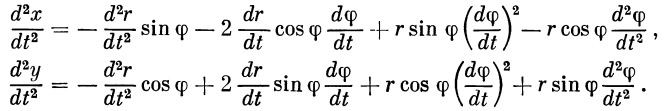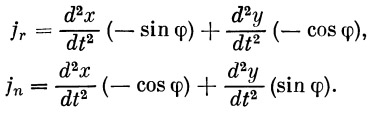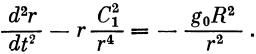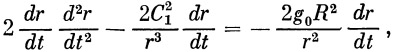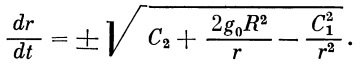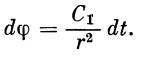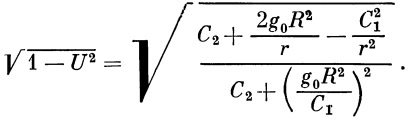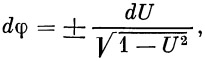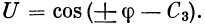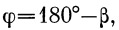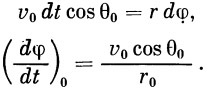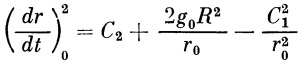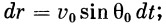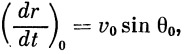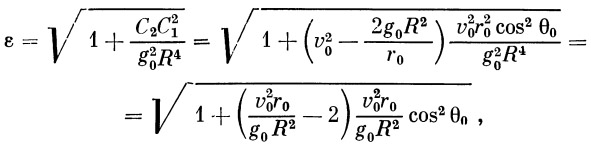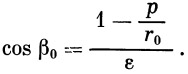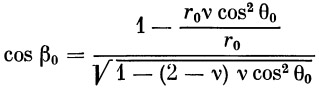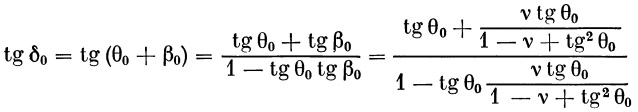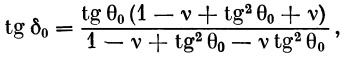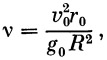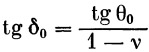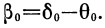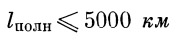Уравнение движения ракеты в вертикальной плоскости (6 видео)

Физические основы полета ракет

Лекция 3
ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛЕТА РАКЕТ.
1. Силовые факторы определяющие полет ракет.
1.1. Схема действующих сил.
1.2. Сила тяги ракетного двигателя.
1.3. Аэродинамические силы и моменты.
2. Общие уравнения движения ракет.
3. Основные траекторные характеристики неуправляемого полета.
3.1. Траектория и дальность полета.
3.2. Рассеивание неуправляемых ракет.
4. Стабилизация реактивного снаряда на траектории.
4.1. Аэродинамическая стабилизация.
4.2. Гироскопическая стабилизация турбореактивных снарядов.

ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛЕТА РАКЕТ.

1. Силовые факторы определяющие полет ракет.
1.1. Схема действующих сил.
1.2. Сила тяги ракетного двигателя.
1.3. Аэродинамические силы и моменты.

2. Общие уравнения движения ракет.

3. Основные траекторные характеристики неуправляемого полета.
3.1. Траектория и дальность полета.
3.2. Рассеивание неуправляемых ракет.

4. Стабилизация реактивного снаряда на траектории.
4.1. Аэродинамическая стабилизация.
4.2. Гироскопическая стабилизация турбореактивных снарядов.

1. Силовые факторы определяющие полет ракет.

1.1. Схема действующих сил.
На ракету в полете действуют три основные силы: сила тяги двигателя (P), аэродинамическая сила (R) и сила тяжести (G).
Сила тяги основного двигателя действует в направлении продольной оси ракеты или близко к ней. Направление суммарной аэродинамической силы за-висит от угла между вектором скорости движения ракеты и ее продольной осью. Направление действия силы тяжести, как правило, не совпадает с двумя предыдущими.
В общем случае вектор суммарной (равнодействующей) силы не проходит через центр масс ракеты, поэтому обычно дополнительно возникает момент этой силы относительно центра масс. На рис. 1 представлена схема действующих на ракету сил для упрощенного варианта нахождения траектории полета в вертикальной плоскости. Здесь же показаны три основные системы координат: земная (x0,y0,z0), связанная (x1,y1,z1) и поточная (x,y,z).
За начало земной системы координат принята точка старта или другая неподвижная относительно Земли точка. Ось ординат направлена по радиусу Земли, ось абсцисс совпадает с направлением на цель, а ось 0Z направлена вправо, если смотреть по направлению оси 0Х, и перпендикулярна двум первым. Эта правая прямоугольная система координат. На чертежах и схемах обычно ось ординат расположена вертикально, а ось абсцисс – горизонтально.
Связанная, или, как ее иногда называют, подвижная, система координат жестко соединена с ракетой и перемещается вместе с ней. Начало координат обычно расположено в центре масс ракеты. Одна из осей координат направлена по продольной оси ракеты, остальные две – перпендикулярно продольной оси ракеты и друг другу. Если ракета выполнена по самолетной схеме, то одна из осей связанной системы координат направлена вдоль хорды профиля крыла, а другая – перпендикулярно ей в плоскости симметрии.
В поточной (скоростной) системе координат одна из осей совпадает с направлением вектора полета центра массы ракеты, другая, ей перпендикулярная, лежит в плоскости симметрии летательного аппарата. Как и предыдущие, поточная система координат является правой прямоугольной системой.
Связь между земной и подвижной системами координат осуществляется с помощью углов тангажа, крена и рыскания.
Угол, лежащий в плоскости между продольной осью ракеты и ее проекцией на горизонтальную плоскость, называется углом тангажа и обозначается буквой *.
Угол между проекцией продольной оси ракеты на горизонтальную плоскость и земной координатой 0Х0 называется углом рыскания и обозначается. Поворот ракеты относительно продольной оси определяется углом крена .
Связь между подвижной и поточной системами координат осуществляется с помощью угла атаки и угла скольжения. Угол между вектором скорости и продольной осью ракеты называется углом атаки . Угол между вектором скорости V и проекцией продольной оси ракеты на плоскость, проходящую через вектор скорости и перпендикулярную вертикальной, называется углом скольжения .
Угол называется углом наклона к горизонту касательной к траектории (угол между вектором скорости и горизонтальной плоскостью); угол – углом поворота траектории.
Если , то получим движение в одной плоскости, при котором .

1.2. Сила тяги ракетного двигателя.
Для вывода уравнения определяющего силу тяги реактивного двигателя рассмотрим общий случай движения тела переменной массы на примере работы воздушно-реактивного двигателя, через заборный диффузор которого поступает встречный поток воздуха, необходимый для работы двигателя. Одновременно с забором воздуха продукты сгорания топлива вытекают с большой скоростью из сопла двигателя назад, создавая силу тяги.
Изменение массы такого двигателя схематично представлено на рис. 2.

Рис. 2 Схема изменения массы:
а – состав массы до присоединения и отделения частиц; б – состав массы после присоединения и отделения частиц.

Пусть в рассматриваемый момент времени t тело имеет массу m+dm2, движущуюся со скоростью V. За промежуток времени dt масса тела изменится за счет присоединения элементарной массы dm1 и одновременного отделения массы dm2. Согласно гипотезе, заложенной в методе И.В. Мещерского, при-соединение и отделение частиц происходит за бесконечно малый промежуток времени подобно удару. После присоединения частица движется со скоро-стью основной массы тела, а отделившаяся частица, получив скорость, сразу теряет взаимодействие с основной массой тела. На рассматриваемую систему трех масс действуют силы, равнодействующая которых F. В результате взаимодействия между собой масс m, dm1 и dm2 и под действием сил F ско-рость соединенной массы m1+dm1 будет равна . Скорость движения мас-сы dm1 перед присоединением обозначим u, а скорость массы dm2 после от-деления .
Найдем изменения количества движения системы масс m, dm1 и dm2 за промежуток времени dt и приравняем его к импульсу внешних сил:
m (V + dV) – mV + dm1 [ (V + dV) – u ] + dm2(*а – V) = Fdt (1)
Проведя преобразование, пренебрегая слагаемым dm1•dυ и разделив обе части уравнения (1) на dt, получим уравнение движения тела переменной мас-сы в общем случае:***
Уравнение, подобное полученному, впервые было выведено И.В. Мещерским и названо его именем.
Взяв один из частных случаев, рассмотренных И.В. Мещерским при dm1=0 и dm2=dm, получим уравнение вида,

позволяющее описать прямолинейное движение ракеты с реактивным двигателем обычного типа. Таким образом, И.В. Мещерский показал, что уравнение движения тела переменной массы (ракеты) можно описывать так же, как уравнение движения тела постоянной массы, включив в число действующих сил »прибавочную» силу .
Для прямолинейного движения ракеты вертикально вверх И.В. Мещер-ский ввел уравнение:
где m – масса ракеты;
g – ускорение силы тяжести;
p – давление газов;
– величина относительной скорости, которую имеют сгорающие частицы в момент их отделения
– сопротивление воздуха.
Из приведенных уравнений может быть получена формула, определяющая силу тяги реактивного двигателя.
Под силой стендовой тяги понимают равнодействующую сил давления воздуха и истекающих газов, приложенных к неподвижной ракете, находящейся в неподвижной невозмущенной атмосфере. Ракета и атмосфера принимаются неподвижными, чтобы сила тяги не включала силу сопротивления воздуха, возникающую при относительном движении ракеты и атмосферы.

Рис. 3 Схема распределения давления, действующего на неподвижную ракету в неподвижной атмосфере.

Для неподвижной ракеты ).
Уравнение движения (4) превратится в уравнение равновесия:
(5)
Слагаемое в уравнении (5) и будет силой тяги.
Раскроем смысл слагаемого р. Если при определении силы тяги ракета и атмосфера неподвижны, то силы сопротивления воздуха нет, а есть лишь наружное давление. На рис. 3 изображена схема распределения давления, действующего на неподвижную ракету с работающим двигателем. На наружную поверхность действуют силы атмосферного давления р0. Они равны по величине произведению давления на площадь и направлены перпендикулярно той площадке, на которую действуют. Все силы, действующие на боковые поверхности ракеты, уравновешивают друг друга. Так как при работающем двигателе атмосферное давление не действует на выходное сечение сопла, через которое протекают газы, то появится равнодействующая сила р0Sa, направленная в сторону истечения газов (Sa – площадь выходного сечения сопла). В выходном сечении сопла действуют противоположно направленная сила раSa, где ра – давление выходящих газов в этом сечении.
Таким образом, в уравнении (5) следует заменить р на Sa(p0-pa), тогда
(6)
В результате получим уравнение для силы тяги в виде:
, (7)
где mcek – секундный расход газа. Слагаемое mcek•* иногда называют реактивной силой.
В зависимости от назначения ракетные двигатели могут развивать тягу от сотых долей до десятка миллионов ньютонов. Такой огромный диапазон тяг доступен пока только ракетным двигателям. Скорости истечения в химических ракетных двигателях лежат в пределах 2000-4500 м/с, т.е. изменяются не очень значительно. Поэтому абсолютная тяга в основном зависит от расхода рабочего тела, который, например, для очень маленьких микродвигателей составляет 10-4 кг/с, а для двигателей ракет-носителей может быть 103 кг/с. Помимо абсолютных значений тяги, важным параметром, оценивающим экономичность использования рабочего тела, является удельный импульс Iy. Обыч-но этим термином называют силу тяги, получаемую от каждого кг массы ра-бочего тела, расходуемого в секунду,
, м/с, (8)
т.е. удельный импульс характеризуется скоростью истечения.
Иногда все еще используют термин удельная тяга Руд, за которую принимают величину силы тяги, отнесенную к секундному весовому расходу топлива в земных условиях. Руд можно рассчитать по формуле:
. (9)
Удельная тяга, в g(

10) раз меньше, чем удельный импульс.

1.3. Аэродинамические силы и моменты.

При движении летательного аппарата в воздушной среде возникают аэродинамические силы, распределенные по поверхности планера. Все эти силы можно привести к одной результирующей силе R, приложенной в центре масс и результирующему моменту М относительно центра масс (см. рис. 4). При изучении движения ЛА или его прочностных характеристик удобнее рассмат-ривать не результирующие силовые факторы, а их проекции на ось какой-либо системы координат (в данном случае скоростной или связанной соответ-ственно).
Проекции вектора полной аэродинамической силы на скоростные оси координат получим наименование:
Х – лобовое сопротивление;
У – подъемная сила;
Z – боковая сила.
Положительное направление лобового сопротивления принято противоположным вектору скорости ЛА.
Вектор полного аэродинамического момента обычно разлагают на составляющие в связанной системе координат:
Mx1 – момент крена;
My1 – момент рыскания;
Mz1 – момент тангажа.
Положительные направления векторов Мх1, Му1, Мz1 совпадают с направлениями соответствующих осей.
Величины аэродинамических сил и моментов зависят от скорости полета, параметров воздуха, формы и размеров ЛА, а также его ориентации относительно вектора скорости в пространстве характеризуемой углами и . Это нашло отражение в основных расчетных зависимостях, количественно определяющих рассматриваемые аэродинамические факторы:

Безразмерные коэффициенты Сх, Су, Сz, mx, my, mz называются аэродинамическими коэффициентами соответствующих сил и моментов.

2. Общие уравнения движения ракет.
При баллистических расчетах ракету обычно принимают за твердое недеформируемое тело. Из механики известно, что характеристики движения твер-дого тела могут быть определены через поступательное движение центра мас-сы тела и вращательное движение вокруг центра масс, т.е. положение твердо-го тела в пространстве определяется шестью независимыми величинами, на-зываемыми степенями свободы. В рассматриваемом случае три из них – коор-динаты центра масс, а три другие – углы возможного поворота продольной оси ракеты относительно центра массы. В соответствии с этим, движение ЛА может быть описано шестью дифференциальными уравнениями. Из них три уравнения поступательного движения в проекциях на земные оси координат имеют вид:

а три уравнения вращательного движения в проекциях на связанные оси координат могут быть представлены как…
где – суммы проекций моментов всех внешних сил на связанные оси координат;
Jx1, Jy1, Jz1 – моменты инерции ракеты относительно осей координат;
– проекции угловой скорости на связанные оси.
Однако неизвестных значительно больше и шести уравнений оказывается недостаточно.
Необходимо знать зависимость от времени: координат центра массы ракеты (х,у,z); проекций скорости центра массы на координатные оси , проекций вектора мгновенной угловой скорости вращения продольной оси ракеты на координатные оси , углов тангажа, рыскания и крена
Так как неизвестных оказывается двенадцать, то к шести уравнениям динамики ЛА должно быть добавлено еще шесть кинематических уравнений.
Первые три из них связывают изменение земных координат ЛА с проекциями его скорости на соответствующей оси:

Производные во времени от углов определяются известными уравнениями
Таким образом, для нахождения двенадцати неизвестных имеем двенадцать уравнений и задача определения характеристик движения неуправляемой ракеты может быть решена.
В общем случае эта задача может решаться в двух постановках.
Если известны силы и моменты, то неизвестными будут перечисленные двенадцать характеристик движения, которые и определяются при решении систем уравнений.
Во втором случае может быть задана часть характеристик движения: величины координат, скоростей или углов. Характеристики движения ракеты задаются в функции от времени или других величин, например у=f1(x) или *=f2(t) и т.д. Эти функции носят название программных уравнений. В этом случае неизвестными будут управляющие силы и моменты, которые должны обеспечить заранее заданную программу движения.
Дополнительные сложности, не отраженные в написанных уравнениях, заключаются в том, что силы и моменты взаимосвязаны с характеристиками движения.
Еще большие сложности вызывает описание управляемого полета, т.к. в этом случае необходимо дополнительно ввести уравнения, описывающие работу системы управления и управляющие силы.

3. Основные траекторные характеристики
неуправляемого полета.

При создании ракет любого класса прежде всего необходимо определить максимальную дальность и реализуемую точность полета.

3.1. Траектория и дальность полета.

Траектория полета (путь движения) неуправляемого РС класса »Земля-земля» содержит активный (ОА) и пассивный (АС) участки (см. рис. 7), при этом большую протяженность имеет пассивный или баллистический участок……..

Скачать полную версию работы

СКАЧАТЬ работу l-raketostroenie/lekcii_raketostroenie_03.rar

Видео:Модуль 2. Баллистика. Равноускоренное движение в плоскости.Скачать

Дифференциальные уравнения движения баллистической ракеты

Рассмотрим движение ракеты в одной плоскости. Для участка выведения баллистической ракеты такой упрощенный подход не ведет к сколь-либо заметным погрешностям.

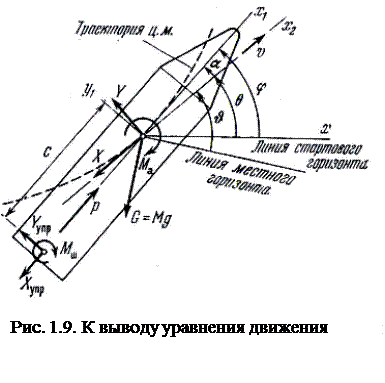
На рис. 1.9 показана система сил, действующих на ракету при плоском движении. При этом плоскости x₁y₁ и х₂у₂предполагаются совпадающими с вертикальной плоскостью ху.

Согласно закону Ньютона произведение массы ракеты М на тангенциальное ускорение dv/dt= и равно сумме проекции сил на касательную к траектории. В итоге получаем:

(1.2)

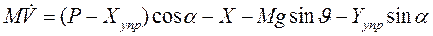
Специфические особенности движения ракеты как тела переменной массы здесь уже учтены в выражении тяги Р.

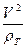
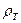
Нормальное ускорение, обусловленное искривлением траектории, равно, как известно, , где — радиус кривизны траектории. (На рис. 1.9 траектория показана с положительной кривизной; в действительности ее кривизна отрицательна.)

Выражение кривизны может быть написано в виде

где θ —угол наклона касательной к траектории, отсчитываемый от неподвижного стартового горизонта (рис. 1.9), a ds — элемент дуги траектории.

Таким образом, нормальное ускорение, направленное к центру кривизны, оказывается равным .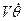

Спроектировав все силы на нормаль к траектории полета, получим:

. (1.3)

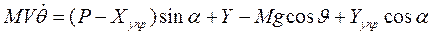
Остается составить еще одно уравнение, связанное с вращением ракеты как жесткого целого в плоскости тангажа.

Угловое ускорение ракеты определяется второй производной от угла φ по времени. Если бы масса ракеты оставалась неизменной, то искомое уравнение мы получили бы, приравняв произведение I сумме моментов, показанных на рис. 1.9. Но дело в том, что I — момент инерции ракеты относительно поперечной оси зависит от времени. Поэтому, для того чтобы составить уравнение вращательного движения в этом простейшем случае, необходимо предварительно проделать операции, подобные тем, которые производились нами ранее при выводе уравнения поступательного движения тела переменной массы.

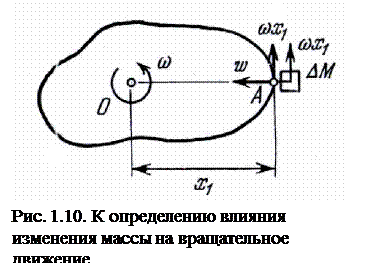
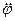
Представим себе некоторое тело (рис. 1.10), которое вращается относительно оси 0 с угловой скоростью ω. Пусть за время Δt к этому телу в радиальном направлении в точке А на расстоянии x₁от оси с нулевой относительной круговой скоростью присоединяется масса ΔM. Момент количества движения тела после присоединения массы ΔM мы формально записываем в виде:

Приравняв изменение момента количества движения импульсу моментов M_i внешних сил, получим:

где ωx₁— поперечная составляющая скорости присоединяемой массы, а 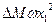— ее момент количества движения до присоединения.

Затем перейдем к пределу. Тогда

где 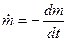— радиальный секундный массовый расход.

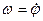
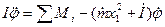
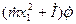
В нашем случае . Поэтому . Слагаемое , имеющее размерность момента, как раз и отражает специфику переменной массы в условиях вращательного движения. Эту величину можно одновременно трактовать и как некоторый демпфирующий момент кориолисовых сил, возникающих в результате поворота потока частиц, движущихся в баках, трубопроводах и камере двигателя. Подробнее мы поговорим об этом при рассмотрении демпфирующих моментов, действующих на ракету.

Теперь можно написать уравнение вращательного движения в плоскости полета в следующем виде:

(1.4)

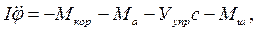
где момент кориолисовых сил

(1.5)

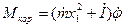
Система дифференциальных уравнений (1.2) —(1.4) еще не является полной, и не только потому, что описывает движение ракеты в одной плоскости. Как раз для целей баллистических расчетов модель плоской траектории позволяет в достаточной мере точно определить все интересующие нас траекторные параметры. Дело совсем в другом.

Уравнения следует дополнить условиями выведения ракеты на активном участке траектории. А это, как мы знаем, обеспечивается, прежде всего, программой изменения угла тангажа.

Таким образом, на три полученных уравнения накладывается условие:

(1.6)

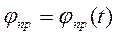
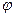
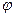
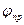
Но коль скоро угол заранее известным образом зависит от времени, уравнение (1.4) теряет свою дифференциальную форму и превращается в некоторую функциональную зависимость входящих в него величин. Так бы оно и было, если бы ракета в своем движении точно следовала нашим предписаниям. Но фактический угол тангажа в уравнении (1.4) и номинальный программный угол в выражении (1.6) — не одно и то же. В реальных условиях полета ракета совершает некоторые угловые колебания относительно поперечных и продольной осей. Частота и амплитуда этих колебаний зависят, конечно, от моментов инерции ракеты, но главное, — от изменения управляющих усилий во времени, в данном случае — от Y_упр. А управляющие усилия, в свою очередь, зависят от принципиальной схемы и параметров настройки автомата стабилизации. Значит, система уравнений (1.2) — (1.4) должна быть дополнена еще уравнениями управления, которые указывают нам, каким образом Y_упр зависит от фактического угла тангажа. Но об этом речь еще впереди.

Сейчас же следует отметить, что уравнения движения (1.2) — (1.4) могут быть положены в основу решения двоякого рода задач: с одной стороны, — баллистических, а с другой, — задач устойчивости, управления и стабилизации. Баллистика как раздел механики дает нам закон движения центра масс: координаты, скорость, ускорение номинального движения в зависимости от времени. Теория устойчивости движения, со своей стороны, отвечает на вопрос о том, в какой мере в реальных условиях выдерживается угловая ориентация ракеты на траектории. Первый класс задач для участка выведения баллистических ракет, как мы уже сказали, в проектной постановке относительно безболезненно вписывается в схему плоского движения. Для полного решения задач второго типа необходимо рассматривать угловые перемещения по всем трем осям.

Возвращаясь к структуре уравнений (1.2) — (1.4),.мы видим, что входящие в них величины остаются пока нераскрытыми. Чтобы произвести интегрирование, необходимо знать, что от чего и как зависит.

Совершенно ясно, что аэродинамические силы зависят от скорости, высоты полета и угловой ориентации ракеты относительно потока. Сила тяги не остается постоянной; она меняется хотя бы уже потому, что с высотой меняется атмосферное давление, а, кроме того, может меняться и расход компонентов. Масса ракеты во времени уменьшается в соответствии с расходом топлива. Наконец, даже ускорение силы тяжести g, если речь идет о больших высотах, должно рассматриваться как величина переменная.

Все эти вопросы мы сейчас и рассмотрим. Начнем со свойств атмосферы и аэродинамических сил.

Видео:Уравнение движенияСкачать

Уравнение движения ракеты в вертикальной плоскости

С.П. Королёв
Основы проектирования
баллистических ракет дальнего действия
(курс лекций)

МВТУ ИМ. БАУМАНА 1949

ЛЕКЦИЯ ПЕРВАЯ

Вторая, основная, часть курса лекций, прочитанного С. П. Королевым в 1949 г. на Высших инженерных курсах, организованных при Московском высшем техническом училище им. Н. Э. Баумана для переподготовки инженеров различных специальностей для работы в ракетостроительной промышленности. Этот курс, в котором был использован и обобщен опыт работы ОКБ по созданию ракет, сразу же изданный в МВТУ в качестве учебного пособия, явился первым в мире систематизированным, достаточно подробным и завершенным курсом основ проектирования жидкостных БРДД, и поэтому он лег в основу преподавания этой дисциплины в институтах, готовящих специалистов по ракетостроению. В настоящем сборнике* работа печатается по изданию МВТУ, 1949 г.

[* Имеется ввиду сборник «Творческое наследие академика Сергея Павловича Королева. Избранные труды и документы» / Под общей редакцией академика М. В. Келдыша — Издательство «Наука», 1980 г.]

1. Баллистический анализ

Обычно основной задачей, которая ставится перед проектантом ракеты дальнего действия, является переброска требуемого боевого груза на заданное расстояние.

В зависимости от метода конструктивного решения поставленной задачи можно указать три основных класса таких ракетных аппаратов:

1-й класс — ракеты так называемой нормальной баллистической схемы, например по типу ракеты с двумя подвесными баками (ракета 2ПБ).

2-й класс — составные ракеты. В этом случае система состоит из ракеты несущей и ракеты несомой, которая отделяется от первой на некоторой высоте. Число ступеней отделения, вообще говоря, может быть сколь угодно велико.

Схемы таких ракет были разработаны К. Э. Циолковским.

3-й класс — крылатые ракеты, использующие подъемную силу крыльев для увеличения дальности полета за счет планирования на пассивном участке полета. В некоторых случаях полет с крыльями может происходить и с работающим двигателем.

В дальнейшем изложении в основном будут рассматриваться главнейшие вопросы проектирования ракет 1-го класса Нормальной баллистической схемы.

В первую очередь рассмотрим инженерную методику расчета траектории и определения основных летных характеристик ракеты.

Вывод уравнений движения ракеты в самом общем виде, с учетом всех факторов, достаточно сложен. Практика работы наших конструкторских бюро показала, что принятая упрощенная инженерная методика расчета траектории вполне оправдывает себя с допустимой степенью точности. Произведенные сравнительные расчеты, а также обработка результатов пусков ракет показывают, что сумма неточностей лежит в пределах порядка 2—3%. Необходимо учитывать также, что в процессе проектирования ряд величин и параметров выбирается с возможными отклонениями в значительно более широких пределах, чем приведенные выше цифры.

1.1. Расчет активного участка

Уравнения движения центра тяжести ракеты в декартовых осях, неподвижно связанных с Землей, мы пишем при следующих основных допущениях.

1. Предполагается, что ось ракеты совпадает с касательной к траектории центра тяжести, т. е. векторы скорости полета ракеты V и реактивной силы P совпадают. Это допущение означает, что мы будем полагать угол атаки а ракеты равным нулю, а следовательно, пренебрегать влиянием на траекторию аэродинамической подъемной силы.

Сравнение приближенных расчетов при указанном допущении с расчетами по точной методике, а также с результатами экспериментов показывает, что ошибка в значении скорости в приближенном расчете не выше 1—1,5%. Ошибка в величине координат, хотя и несколько больше (вследствие изменения формы траектории), однако ею также вполне можно пренебречь при практическом проектировании.

2. Далее, коэффициент силы лобового сопротивления ракеты С_х принимается постоянным, не зависящим от угла атаки.

3. Пренебрегаем изменением силы сопротивления газовых рулей при их отклонении. Ошибки, получающиеся из-за указанного допущения, невелики и при подсчете скорости не превосходят

Следует отметить, что абсолютное значение сопротивления рулей необходимо брать с учетом обгорания их.

Для ракеты 2ПБ потери тяги в этом случае составят порядка 1,4-1,8 т .

4. Пренебрегаем влиянием вращения Земли, что вызывает ошибки, меньшие 1% для рассматриваемой нами ракеты.

5. Полагаем секундный расход топлива неизменным в течение всего времени работы двигателя.

G — вес ракеты ( кг ),

m — масса ракеты ( кг • сек 2 / м ),

g — ускорение силы тяжести ( м / сек 2 ),

v — скорость полета ( м / сек ),

X — сила лобового сопротивления ( кг ),

θ — угол касательной к траектории с осью х .

Проектируя действующие силы на направление касательной к траектории и относя их к массе m , получаем следующее уравнение движения (рис. 1):

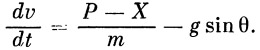Уравнение движения ракеты в вертикальной плоскости

(1)

К уравнению (1) мы добавляем два уравнения:

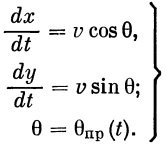(2)

Уравнения (1) и (2) необходимо дополнить уравнением программы, обеспечивающей заданную форму траектории и нужный угол θ в конце активного участка.

Зависимость θ = θ _пр( t ) задается графически или в виде таблицы.

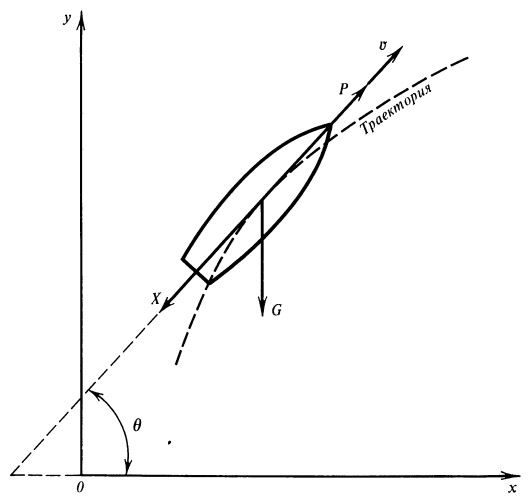Рис. 1.
К выводу уравнений движения

Расчеты по упрощенной схеме, представленной уравнениями (1) и (2), достаточны для проверки основных проектных характеристик.

В уравнение (1) входят величины Р , X и m , о которых кратко можно сказать следующее.

Тяга Р при полете ракеты может определяться по формуле

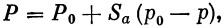(3)

где Р ₀ — тяга, замеренная на стенде Р _ст, с учетом силы сопротивления неотклоненных газовых рулей Х _газ:

Сопротивление неотклоненных газовых рулей ракеты 2ПБ составляет в среднем 1400—1800 кг .

В случае отклонения газовых рулей их сопротивление может резко увеличиваться. Однако при этом необходимо иметь в виду также и то обстоятельство, что геометрия газовых рулей по мере работы двигателя сильно изменяется вследствие их постепенного обгорания.

Поэтому вопрос о величине дополнительного сопротивления пока не может быть решен достаточно точно, и во всех расчетах можно ориентироваться на приведенные цифры.

S_a означает площадь выходного сечения сопла, р ₀ — атмосферное давление у поверхности Земли, р — давление в атмосфере на данной высоте.

Масса ракеты может определяться по формуле

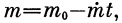(4)

где m — масса ракеты в момент t , m ₀ — масса ракеты в момент t =0, ṁ — секундный массовый расход топлива, t — время в секундах.

Сила лобового сопротивления ракеты определяется по формуле

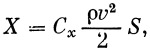(5)

где С _х — коэффициент силы лобового сопротивления, ρ — плотность воздуха на высоте полета (( кг / м 4 )• сек 2 ), v — скорость полета ( м / сек ), S — площадь миделя ракеты ( м 2 ).

Все численные значения основных величин, а также интегрирование системы уравнений (1) и (2) нами здесь не рассматриваются, так как вопросу численного интегрирования указанных уравнений будет посвящено специальное практическое занятие.

1.2. Пассивный участок полета

Пассивный, или свободный, участок полета ракеты, т. е. движение ее после окончания работы двигателя, является движением по инерции. Живая сила, приобретенная ракетой на активном участке, расходуется на преодоление сопротивления воздуха и силы тяготения.

Мы разбиваем расчет свободного участка на две части. В первой части учитываем действие сопротивления воздуха и поля тяготения, а во второй — ограничиваемся учетом лишь поля тяготения. Система координат и обозначения, принимаемые нами при расчете первого участка свободного полета, поясняются на рис.

2. Если обозначить индексами х и у проекции соответствующих векторов на оси координат, то уравнения движения центра тяжести ракеты примут вид

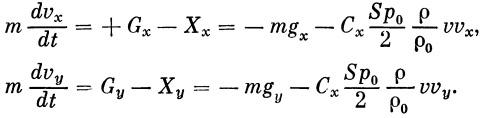(6)

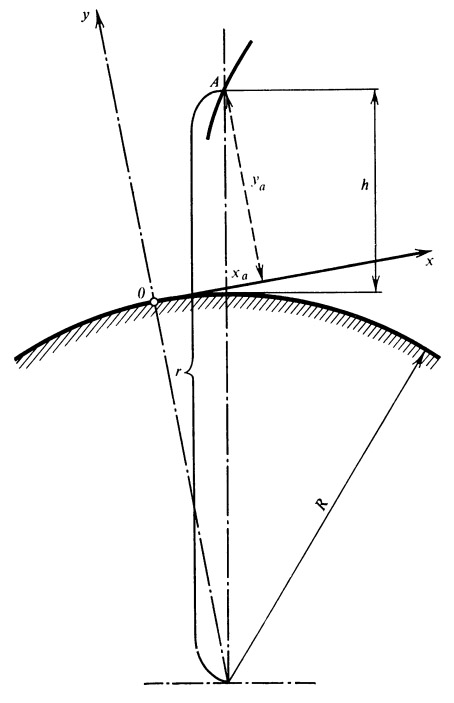Рис. 2.
Система координат и основные обозначения для первого участка свободного полета

Значения Х _х и Х _у получаются [в виде]

Разделив уравнения (6) на m и добавляя два кинематических уравнения, получим систему уравнений (7), достаточную для проведения численного интегрирования и определения параметров интересующего нас участка:

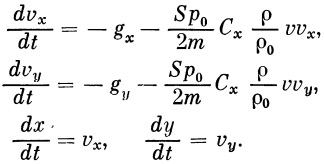(7)

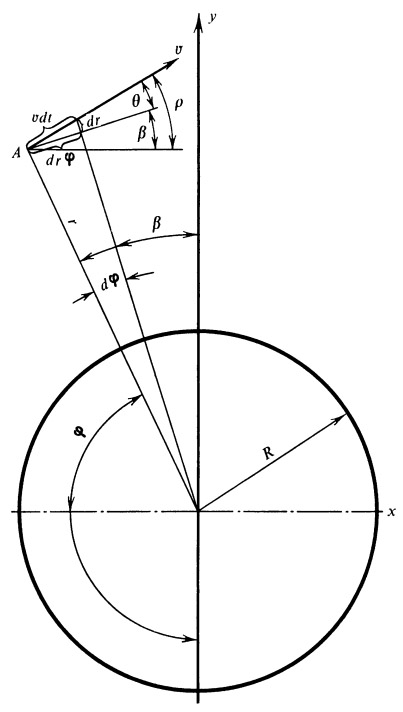Рис. 8.
Система координат и основные обозначения для второго участка свободного полета

Высота h в случае необходимости может быть определена по формуле

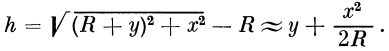(8)

В результате численного интегрирования системы уравнений (7) мы получаем координаты центра тяжести ракеты, ее скорость, а также угол наклона касательной к траектории для момента времени, после которого силой сопротивления воздуха можно пренебречь.

Эти параметры будут начальными условиями для расчета второй части свободного участка, где учитываем только силы тяготения. К расчету этого участка мы и перейдем. Принятые обозначения поясняются рис. 3.

Для движущейся точки А могут быть написаны следующие соотношения:

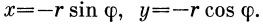(9)

Дифференцируя еще один раз, имеем

Обозначим: j _r — ускорение ракеты по направлению радиус-вектора; j _n — ускорение ракеты по нормали к радиус-вектору. Очевидно, что

После подстановки в эти уравнения значений d 2 x / dt 2 и d 2 y / dt 2 и соответствующих преобразований, получим

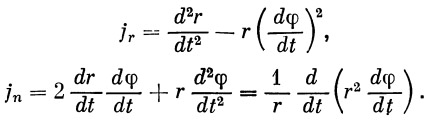(10)

Напишем уравнение движения нашей ракеты в полярной системе координат ( r , φ ). Учитывая, что

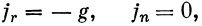(11)

где g — ускорение на высоте полета ракеты, и подставляя в уравнения (10) значения j _r и j _n из уравнений (10), получим

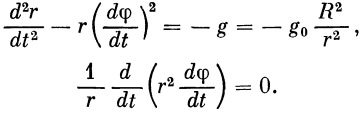(12)

Из последнего уравнения следует известный закон Кеплера

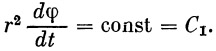(13)

Из уравнения (13) мы найдем dφ / dt и, подставляя его в первое уравнение системы (12), получим

Умножим обе части последнего уравнения на 2 ( dφ / dt ):

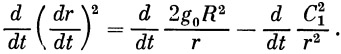(14)

Интегрируем уравнение (14):

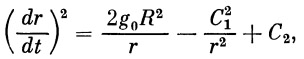(15)

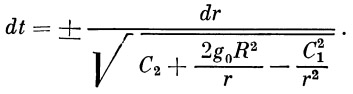(16)

Из уравнения (13) имеем

Подставляем сюда выражение для dt из (16):

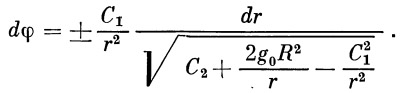(17)

Для интегрирования уравнения (17) введем подстановку

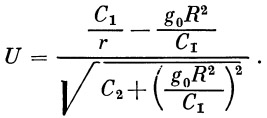(18)

Теперь вместо дифференциального уравнения (17) мы можем написать следующее:

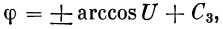(19)

Из выражения (18) находим значение радиуса r :

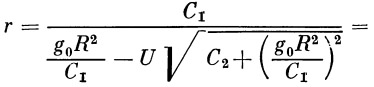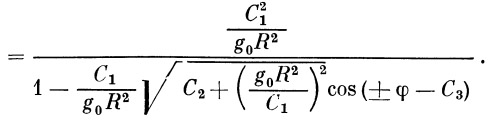(20)

Выбирая соответствующим образом начало отсчета угла φ , из последней формулы можно получить

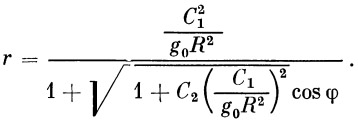(21)

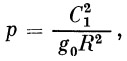(22)

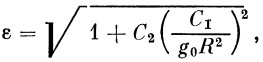(23)

то из (21) следует

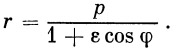(24)

Это уравнение представляет собой уравнение эллипса. Так как ось у проходит через вершину траектории, то введем в качестве координатного (полярного) угла угол β вместо угла φ :

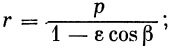(25)

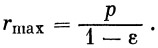(25′)

Определим постоянные величины, введенные в процессе интегрирования.

У нас имеются две произвольные постоянные C ₁ и С ₂ и два сокращенных обозначения р и ε .

Если момент начала свободного участка ракеты в поле тяготения (без учета сил сопротивления воздуха) совместить с моментом конца сгорания топлива, то тогда параметры точки конца горения будут одновременно начальными условиями для свободного участка.

Пусть ракета в начале свободного участка находилась в точке А (см. рис. 3). Всем величинам, характеризующим положение и скорость ракеты в этот момент, мы присваиваем индекс «нуль». Тогда из рис. 3 легко устанавливаем, что

Сопоставляя с уравнением (13), получим

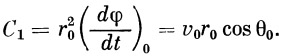(26)

Далее, из уравнения (15) имеем

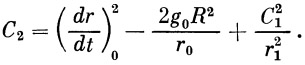(27)

Величина ( dr / dt )₀ определяется из рис. 3:

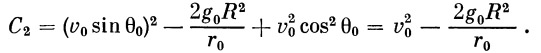(28)

Константа С ₃ нами исключена из рассмотрения надлежащим выбором начала координат, что учитывается формулой (21).

Прежде чем выразить оставшиеся константы через известные величины, введем обозначение, чрезвычайно важное в дальнейших расчетах:

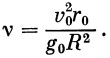(29)

Здесь, как и выше, g ₀ означает ускорение на поверхности Земли, v ₀ и r ₀ — скорость ракеты и ее радиус-вектор в конце активного участка.

Согласно обозначению (22), находим

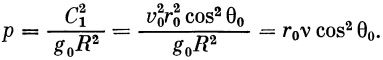(30)

В соответствии с (23) получим

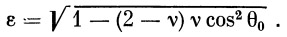(31)

Далее, из выражения (25), решенного относительно β ₀,

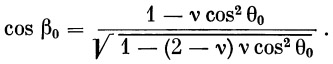(32)

Переходя от cos β ₀ к tg β ₀ по формуле

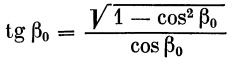(33)

и подставляя в формулу (33) выражение для cos β ₀ из (32), получим

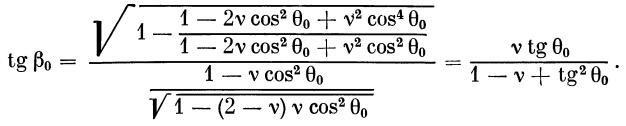(34)

Если равенством δ ₀= θ ₀+ β ₀ ввести угол δ ₀, то формулы можно значительно упростить:

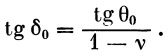(35)

Полученные формулы позволяют сразу решить все интересующие нас вопросы, связанные с расчетом свободного участка.

По известным начальным условиям (конец активного участка) вычисляется параметр v по формуле B9)

далее по формуле

находим угол δ ₀ и вычисляем β ₀:

По известному углу B ₀ определяем «эллиптическую» дальность l _эл. Параметры движения в конце эллиптического участка (точка В ) принимаются за исходные для расчета дальности нисходящего участка траектории l _нисх. Обозначения поясняются рис. 4.

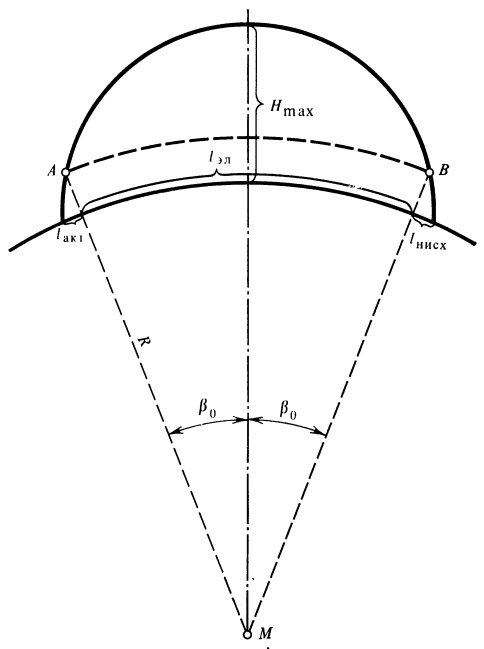Рис. 4.
К расчету дальности полета

«Эллиптическая» дальность вычисляется по следующей формуле:

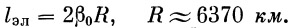(36)

Полная дальность ракеты вычисляется по формуле

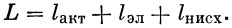(37)

Максимальная высота подъема, т. е. вершина траектории, определится выражением

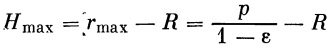(38)

(на основании формулы (25′))

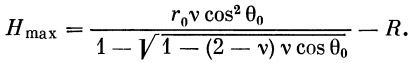(39)

На начальной стадии проектирования необходимость проведения серии подсчетов даже по таким сравнительно простым формулам все-таки связана с затратой значительного времени.

Поэтому для прикидочных расчетов может быть рекомендована простая номограмма, позволяющая с достаточным приближением и быстро производить такие расчеты.

Номограмма приведена на рис. 5.

При пользовании предложенной номограммой необходимо сделать следующее замечание.

Сравнение величин l _акт+ l _нисх с величиной l _полн показывает, что до дальностей

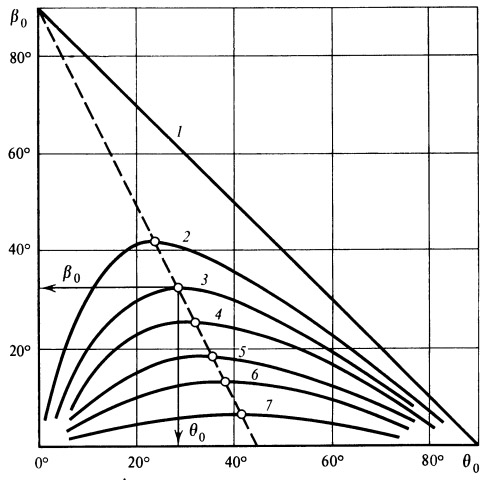Рис. 5.
Номограмма для расчета дальности

1 — v = l; 2 — 0,8; 3 — 0,7; 4 — 0,6; 5 — 0,5; 6 — 0,4; 7 — 0,2

Поэтому с достаточным приближением можем считать

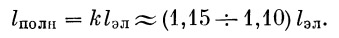(40)

Учитывая последнее обстоятельство, при определении основных проектных параметров мы можем пользоваться номограммой, построенной только для дальности эллиптического участка.

Рассмотрим некоторые задачи, решаемые с помощью номограммы.

1. Пусть нам задана величина v . Требуется определить возможную максимальную дальность. По номограмме при заданном v из условия оптимума находим β ₀ и θ ₀, затем по формуле (36) определяем l _эл, по формуле (40) находим l _полн.

2. Пусть задано l _полн. Требуется определить оптимальные параметры. Зная l _полн, по формуле (40) находим l _эл, а по формуле (36) определяем β ₀

Далее используем номограмму: задаваясь найденным углом β ₀ определяем v _min и соответственно оптимальный угол θ ₀. По величине v _min находим минимально необходимую начальную скорость v ₀.

3. Задано θ ₀. Требуется определить v ₀, при которой этот угол имеет оптимальное значение.

Требование определения v ₀, удовлетворяющей поставленной задаче, аналогично отысканию такого v , при котором заданный угол дает максимальное значение дальности.

По номограмме легко видеть, что оптимальные условия можно найти не для любого угла θ , а только для θ ₀≤45°.

Следует подчеркнуть, что ценность номограммы заключается в получении первого ориентировочного подсчета основных величин лишь в начальной стадии проектирования.