Уравнение диффузии для мембраны коэффициент проницаемости

Одна из основных функций биологической мембраны – селективный транспорт веществ. Принято различать

· пассивный транспорт – происходящий в направлении действия электрохимического градиента (концентрационного, электрического и т.д.);

· активный транспорт – процессы переноса веществ против существующих градиентов и требующие затрат энергии.

Пассивный транспорт объединяет ряд механизмов переноса веществ.

Диффузия – самопроизвольное перемещение вещества из области большей концентрации в область меньшей концентрации вследствие хаотического теплового движения молекул. Уравнение диффузии (уравнение Фика) имеет вид:

,

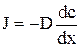
где J – плотность потока – количество вещества переносимое через единицу площади за единицу времени [моль/м 2 ×с]; – градиент молярной концентрации; D – коэффициент диффузии [м 2 /с]:

,

где R – универсальная газовая постоянная (8,31 Дж×моль –1 ×К –1 ); Т – абсолютная температура (К); N_A – постоянная Авогадро (6,02×10 23 моль –1 ); r – радиус диффундирующих частиц (м); h — вязкость среды (Н×с/м 2 ). Таким образом, скорость диффузии будет зависеть от температуры, вязкости растворителя и размера частиц.

Для расчета диффузии через биологическую мембрану часто используют формулу:

,

где Р – коэффициент проницаемости; с_i и с₀ – молярная концентрация частиц в клетке и снаружи. Коэффициент проницаемости прямо пропорционален коэффициенту диффузии (D), коэффициенту распределения вещества между водным раствором и липидной фазой мембраны (k) и обратно пропорционален толщине мембраны (l):

Коэффициент распределения тем выше, чем легче вещество растворяется в липидной фазе. Следовательно, переход гидрофильных соединений непосредственно через липидный бислой будет крайне затруднен (так, молекулы пропиленгликоля диффундируют через мембрану примерно в 20 раз быстрее, чем молекулы мочевины).

Если происходит перенос заряженных частиц (ионов), то помимо концентрационного градиента необходимо учитывать величину разности потенциалов биологической мембраны. Уравнение диффузии для таких частиц называется уравнением Нернста-Планка и имеет вид:

,

где u_m – подвижность диффундирующих частиц выраженная для моля (u = u_m×N_A); Z – заряд иона; F – постоянная Фарадея; с – молярная концентрация ионов; – градиент мембранного потенциала.

Кроме диффузии через липидный бислой мембраны транспорт веществ может происходить через липидные поры и белковые каналы (рис. 4).

	а) диффузия через липидный бислой; б) диффузия через липидную пору; в) диффузия через белковый канал.
Рис. 4. Диффузионный транспорт через мембрану.

Мембранный канал представляет собой интегральный белок (белковый комплекс, гликопротеид), пронизывающий липидныйкаркас мембраны и обеспечивающий перенос веществ через мембрану в сторону более низкого электрохимического потенциала. Вторичная структура белкового комплекса имеет b-складчатый характер с цилиндрической полостью внутри, заполненной водой. Коэффициент проницаемости ионных каналов для гидрофильных веществ составляет 10 –8 -10 –9 м/с, что на 5-6 порядков меньше скорости переноса ионов в водной среде, но значительно превышает скорость их диффузии через липидную фазу.

Ионный канал содержит два основных компонента: селективный фильтр и воротный механизм. Первый имеет жесткую структуру, т.е. в этой части белковый комплекс не может изменять размеры поры и регулировать проницаемость мембраны. Функция селективного фильтра – пропускать через канал определенное вещество или группу сходных с ним веществ, т.е. избирательная проницаемость. Регулирование мембранной проницаемости обеспечивается воротными процессами. Они осуществляются «воротами канала», которые представляют собой части белкового комплекса, способные «раскручиваться» и «скручиваться» в ходе их механохимических реакций и благодаря этому создавать просвет внутри белкового комплекса или перекрывать его (сжимать или восстанавливать пору).

Проницаемость мембраны для данного вещества определяется только числом открытых в данный момент каналов. Поэтому мембранную проницаемость (Р) при переносе веществ по каналам рассчитывают по формуле:

,

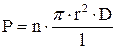
где n – число открытых каналов на единице поверхности; r – радиус канала; D – коэффициент диффузии; l – длина канала (примерно соответствует толщине мембраны).

Переход канала из закрытого состояния в открытое и обратно осуществляется под действием определенных стимулов (сдвиг мембранного потенциала, химические, механические, световые модальности).

Облегченная диффузия происходит с участием специальных переносчиков. Например, антибиотик валиномицин осуществляет перенос ионов калия через мембрану. Его структура напоминает браслет (рис. 5) образованный изнутри полярными группами (обеспечивают связывание калия), а снаружи – неполярными (обуславливают гидрофобность молекулы). Ион калия встраивается в центральную область антибиотика на наружной поверхности мембраны, заряженный комплекс под действием электрического поля диффундирует через мембрану и на ее внутренней стороне распадается. Калий поступает в цитоплазму, а свободная молекула валиномицина возвращается обратно.

	а) транспорт ионов К + через мембрану с помощью валиномицина (V – свободная молекула валиномицина; KV + – комплекс валиномицина с калием); б) структура комплекса К + ‑валиномицин
а)	б)
Рис. 5. Механизм действия валиномицина.

По современным представлениям, аналогично происходит перенос аминокислот, сахаров и ряда других веществ.

Примером фиксированного переносчика является антибиотик грамицидин. Две его молекулы встраиваются в мембрану и формируют полый цилиндр, в котором полярные группы расположены внутри. Скорость переноса ионов может составлять 10 10 с –1 , что примерно в 10 5 раз превышает производительность подвижных переносчиков.

Характерные черты облегченной диффузии:

· для ее реализации обязательно должен существовать концентрационный градиент переносимого вещества;

· при увеличении градиента концентрации скорость облегченной диффузии повышается до определенного предела («насыщение» определяется концентрацией переносчика);

· скорость облегченной диффузии значительно превышает скорость простой, поскольку переносчик приводит к значительному повышению мембранной проницаемости для данного вещества;

· возможна конкуренция близких по структуре веществ за связывание с молекулой переносчика.

Осмос – движение растворителя через полупроницаемую мембрану (непроницаемую для растворенного вещества) в сторону более концентрированного раствора. По своей сути осмос – это простая диффузия молекул воды.

Осмотическое давление измеряется в атмосферах (в СИ – паскали) и определяется по формуле:

где R – универсальная газовая постоянная, 8,31×10 3 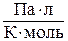; Т – температура, К; С – концентрация растворенного вещества, г/моль; i – изотонический (изоосмотический) коэффициент (для не электролитов i = 1, для разбавленных растворов солей, кислот, щелочей i ≈ 2-3). Сила, противодействующая осмосу – упругое сопротивление мембраны или дополнительная величина гидростатического давления. В тот момент, когда величина осмотического давления уравновешивается противодействующей силой, система переходит в состояние равновесия. Р_осм большинства клеток организма человека составляет около 780 кПа (7,5-8,1 атм). В местах воспаления (опухоли) возможно увеличение до 15-20 атм.

Явление осмоса играет ключевую роль в жизнедеятельности организма, обеспечивая поступление воды через мембраны и тургор или упругость клеток (формообразование, эластические свойства тканей).

По сравнению с осмотическим давлением клеток, внешние растворы могут быть:

· Изотоническими – имеют ту же величину осмотического давления, не вызывают изменения клеточных структур (0,9% водный раствор NaCl называют физиологическим раствором). Для инъекций лекарственных препаратов используются преимущественно изотонические растворы.

· Гипертоническими – растворы с большим осмотическим давлением, приводят к плазмолизу клеток («сморщиванию») вследствие выхода из них воды.

· Гипотоническими – растворы с меньшим осмотическим давлением приводят к разбуханию и разрыву клеточной оболочки – лизису, поскольку вода начинает поступать внутрь клетки. Повязки с гипертоническим раствором (10% NaCl) применяют в медицине при лечении гнойных ран (за счет осмоса происходит ток жидкости из раны и она очищается от микроорганизмов, продуктов распада). Горькую соль (MgSO₄×7H₂O) и глауберову соль (Na₂SO₄×10H₂O) используют как слабительные средства. Они плохо всасываются в желудочно-кишечном тракте, и при применении гипертонических растворов этих солей в просвет кишечника переходит значительное количество воды из слизистой оболочки.

Фильтрация – движение раствора через поры в мембране под действием градиента давления. В общем виде, скорость переноса при фильтрации подчиняется закону Пуазейля:

Фильтрация играет огромную роль в капиллярном транспорте, поскольку обеспечивает перенос воды и растворенных в ней веществ из плазмы крови в тканевую жидкость. Направление и скорость движения воды определяется по формуле:

где Q – объемная скорость движения воды через капиллярную стенку; f – коэффициент фильтрации (определяется вязкостью раствора, количеством пор и т.д.); Р_гк – гидростатическое давление в капилляре; Р_гт – гидростатическое давление в тканевой жидкости; Р_ок – онкотическое давление крови; Р_от – онкотическое давление тканевой жидкости. Онкотическое давление – часть осмотического, создаваемое за счет белковых макромолекул (более мелкие молекулы свободно проходят через капиллярную стенку и не участвуют в формировании осмотического давления). Под действием Р_гк и Р_от жидкость стремится выйти из капилляра в ткань (фильтрация), а под действием Р_гт и Р_ок – возвратиться обратно в капилляр (реабсорбция). Градиент гидростатического давления в капиллярном русле приводит к тому, что в артериальной части артериол происходит фильтрация, а в венозной части – реабсорбция, причем между объемами отфильтрованной и реабсорбированной жидкости в норме существует динамическое равновесие (≈ 10% объема жидкости возвращается из интерстициального пространства в кровяное русло с помощью лимфатической системы).

Активный транспорт идет против существующих электрохимических градиентов и сопровождается ростом энергии Гиббса. Следовательно, он всегда происходит с затратой энергии запасенной в макроэргических связях АТФ. Впервые существование активного транспорта было показано в опытах Уссинга (1949 г).

Камера Уссинга (рис. 6) заполнена раствором Рингера и разделена на две половины кожей лягушки. Наблюдались потоки ионов Na + , при этом внутренняя сторона кожи приобретала положительный заряд по отношению к наружной. С помощью блока компенсации напряжения разность потенциала кожи приводили нулю и поддерживали одинаковую концентрацию ионов по обе стороны мембраны. Если бы транспорт ионов осуществлялся только пассивными механизмами, то потоки ионов через мембрану в обе стороны были бы равны, а ток в цепи отсутствовал. Однако электрический ток продолжал протекать через мембрану, следовательно, происходит однонаправленный перенос заряженных частиц. Метод радиоактивных изотопов показал, что поток ионов Na + внутрь клетки превышает поток из клетки. Дальнейшие опыты показали, что истощение запасов АТФ в коже лягушки приводит к остановке однонаправленного потока ионов Na + .

	А – амперметр, V – вольтметр, Б — батарейка, П – потенциометр.
Рис. 6. Схема опыта Уссинга.

В биологические мембраны встроены сложные белковые комплексы фермента АТФ-азы (ионные насосы), работающие за счет свободной энергии гидролиза АТФ. У человека примерно 30-40% всей энергии, образующейся при метаболических процессах, расходуется на активный транспорт. Активный транспорт обеспечивает формирование в живой системе градиентов концентраций, электрических потенциалов, давления и т.д., то есть поддерживает организм в неравновесном состоянии, что лежит в основе существования жизни. В настоящее время известны три типа электрогенных ионных насосов:

Натрий-калиевый насос	Кальциевый насос	Протонный насос

Транспорт ряда веществ через мембрану не связан непосредственно с процессами гидролиза АТФ, но обусловлен наличием на мембране электрохимических градиентов. Такие механизмы получили название вторичного активного транспорта. Так, перенос сахаров, аминокислот из полости кишечника происходит за счет электрохимического градиента ионов Na + , который, в свою очередь создается работой Na + -K + -АТФ-азы.

Видео:Транспорт веществ через мембрануСкачать

Лекция 3. Проницаемость и транспорт веществ в биологических мембранах

ПРОНИЦАЕМОСТЬ И ТРАНСПОРТ ВЕЩЕСТВ В БИОЛОГИЧЕСКИХ МЕМБРАНАХ

Проницаемость биологических мембран

Одна из важнейших функций биологической мембраны заключается в обеспечении обмена ионов и молекул между клеткой и окружающей средой. Способность биологических мембран пропускать через себя различные вещества называется проницаемостью. Изучение проницаемости клеток имеет большое значение, поскольку с данной функцией связаны практически все процессы жизнедеятельности клетки: метаболизм, генерация и проведение биопотенциалов, секреция, рецепция и т. д.

Любая клетка очень точно поддерживает свой химический, в том числе и ионный состав. Постоянство ионного состава называется ионным гомеостазом и поддерживается за счёт транспорта веществ.

Транспорт веществ в организме можно разделить на три категории:

— дальний транспорт – перенос веществ между органами, его протяжённость в растениях может достигать нескольких десятков метров;

— ближний транспорт – перенос между соседними клетками;

— мембранный транспорт – перенос веществ через мембрану.

По энергетическим затратам мембранный транспорт можно разделить на 2 важнейших класса: активный и пассивный.

Пассивный транспорт не связан прямо с затратой химической энергии; он осуществляется в результате диффузии веществ в сторону меньшего электрохимического потенциала (где концентрация веществ и заряд меньше). Активный транспорт происходит при затрате химической энергии АТФ или переносе электрона по дыхательной цепи.

Виды пассивного транспорта веществ в клетках и тканях: диффузия, осмос.

Диффузия — основной механизм пассивного транспорта веществ, обусловленный наличием концентрационного градиента. Различают несколько видов диффузии:

1) простая диффузия, диффундирующее вещество движется по градиенту через мембрану, не образуя комплекса или проникая через канал;

2) облегченная диффузия, осуществляемая с помощью переносчиков — белков или молекулярных комплексов.

Простая диффузия — это самопроизвольный физический процесс проникновения вещества из области высокой в область меньшей его концентрации в результате теплового хаотического (броуновского) движения молекул.

С помощью простой диффузии через мембрану переносятся растворимые в липидах вещества, в частности такие хорошо растворимые в липидах и важнейшие для метаболического обмена вещества как кислород и углекислый газ. Через липидную фазу мембран в клетку могут проникать также яды и лекарства.

Математическое обоснование процесса диффузии впервые дал А. Фик. Согласно первому закону Фика поток вещества (J) прямо пропорционален градиенту концентрации dC/dx:

,

где D – коэффициент диффузии, см2∙с-1. Коэффициент диффузии зависит от природы вещества, температуры и характеризует способность вещества к диффузии.

Единица измерения J = моль∙см-2∙с-1. Знак «-» означает, что поток направлен в сторону убывания концентрации вещества. Поток вещества — это количество вещества (в молях), диффундирующего за единицу времени через данную площадь.

При исследовании проницаемости клеточной мембраны концентрационный градиент определить трудно, поэтому для описания диффузии вещества через нее пользуются более простым уравнением. Для его получения следует учесть три момента:

1) толщина мембраны постоянна, обозначим её как d;

2) концентрации вещества по обе стороны мембраны постоянны, Cin – концентрация вещества внутри клетки, Cout – концентрация вещества в окружающем клетку растворе;

3) различные диффундирующие вещества имеют разную растворимость в липидной фазе мембраны, которая количественно характеризуется коэффициентом распределения β = Cм/Cр-р, где Cр-р – концентрация вещества снаружи мембраны, а Cм — концентрация вещества внутри мембраны.

В этом случае силой, которая двигает молекулы через мембрану, будет градиент концентрации вещества через мембрану, который выразится в формуле:

Учитывая это, формулу для потока вещества через мембрану можно записать в следующем виде:

Поскольку величины D, β — константы, зависящие только от природы проникающего вещества, а d – характеристика мембраны, через которую это вещество проходит, то эти параметры можно объединить в один, называемый коэффициентом проницаемости и обозначаемый P:

Коэффициент проницаемости Р имеет размерность см/с и является количественной характеристикой способности конкретного вещества проникать через мембрану. Он аналогичен

коэффициенту диффузии (D), но зависит не только от природы вещества и температуры, но и от свойств мембраны.

Проникновение в клетку глюкозы, глицерина, аминокислот и некоторых других веществ не имеет линейной зависимости от их концентрации. Причем при определенных концентрациях скорость их проникновения значительно выше, чем при простой диффузии. Эта особенность объясняется тем, что в данном случае наблюдается не простая, а облегченная диффузия. Вещество самостоятельно диффундирует через мембрану, но скорость диффузии намного возрастает, если молекулы этого вещества образуют комплекс с молекулами переносчика, который хорошо растворяется в липидах. Молекулы-переносчики могут быть как подвижными, так и фиксированными в мембране — каналы.

Диффузия с участием переносчика, как и простая, происходит до тех пор, пока концентрация по обе стороны мембраны не станет одинаковой.

Разновидностью облегченной диффузии является так называемая обменная диффузия, при которой переносчик образует соединении с диффундирующим веществом и перемещается с ним от одной поверхности мембраны к другой, где молекула переносчика освобождается, ее место занимает другая молекула того же вещества и комплекс переносится обратно. При работе переносчиков в случае обменной диффузии концентрация веществ по обе стороны мембраны не изменяется. Существование обменной диффузии было доказано методом меченых атомов на эритроцитах, митохондриях и др.

Проникновение растворенных частиц, обладающих электрическим зарядом, через клеточную мембрану осуществляется по электрохимическому градиенту, а не по концентрационному.

Электрохимический потенциал – энергия, которую надо затратить для перемещения одного моля вещества из бесконечно удалённой точки пространства в данную точку с конкретными условиями.

Величина электрохимического потенциала описывается формулой:

где: — стандартный член;

— активность j-го иона

химическая работа;

— парциальный моляльный обьем;

— механическая работа (работа по расширению объёиа)

— заряд иона;

— электрический потенциал;

— число Фарадея;

— электрическая работа.

Молекулы вещества всегда двигаются в сторону своего более низкого электрохимического потенциала.

Рассмотрим простую систему, представляющую собой два отсека, содержащие раствор соли (например, KCl) и разделённые мембраной, которая пропускает только катион, в нашем случае К+.

Растворы находятся в равновесии, это означает, что электрохимические потенциалы ионов в обоих отсеках одинаковы. Математически это будет выражаться уравнением:

Это уравнение, учитывая, что давления и моляльные объёмы вещества в обоих отсеках одинаковы, позволяет нам рассчитать разность электрических потенциалов между отсеками:

Это уравнение называется уравнением Нернста. Если учесть значения констант перед знаком логарифма, и вместо натуральных логарифмов использовать десятичные, то эту формулу можно записать в виде:

Таким образом, если два раствора разной концентрации разделены мембраной, которая обладает избирательной проницаемостью к компонентам раствора, то между этими растворами возникает разность электрических потенциалов. Если мембрана проницаема для одновалентного иона, то десятикратное изменение концентрации в одном из отсеков вызовет к увеличению разности потенциалов между ними на 59 милливольт.

В растворе помимо молекул растворённого вещества присутствуют и молекулы растворителя. Что будет, если мембрана между отсеками будет непроницаема для молекул растворённого вещества, но будет пропускать молекулы растворителя?

Рассмотрим простую модель – два отсека, разделённые мембраной, способной пропускать молекулы растворителя, например, воды и непроницаемой для молекул растворённых веществ. Для наглядности в первом отсеке концентрация растворённого вещества высокая, а во втором низкая. Выделим в каждом отсеке одинаковые объёмы.

Если записать для каждого отсека электрохимический потенциал молекул растворителя, то сразу становится очевидным, что электрохимический потенциал молекул растворителя в первом отсеке меньше, чем во втором, а это означает, что молекулы растворителя будут двигаться из второго отсека в первый. В реальном эксперименте с осмометром это выглядит, как будто какая-то сила заставляет молекулы растворителя двигаться в сторону большей концентрации растворённого вещества. Это явление — движение молекул растворителя через полупроницаемую мембрану в сторону большей концентрации растворённого вещества называется осмосом, а сила, которая заставляет молекулы воды двигаться – это и есть осмотическое давление.

Осмотическое давление раствора зависит от количества растворенных ионов и температуры. В соответствии с уравнением Вант-Гоффа осмотическое давление (π) раствора прямо пропорционально концентрации (С) растворенного вещества и абсолютной температуре раствора (T):

где i — изотонический коэффициент, зависящий от степени диссоциации электролита и показывающий, во сколько раз увеличивается количество растворенных частиц при диссоциации молекул; для неэлектролитов i = l, для электролитов i > 1; R — газовая постоянная.

Активный транспорт — движение против градиента электрохимического потенциала, осуществляемое с затратой химической энергии за счёт гидролиза АТФ или переноса электрона по дыхательной цепи.

Выделяют первично-активный и вторично-активный транспорт.

Рис. — Активный перенос ионов при работе транспортных АТФ-аз.

Транспорт называется первично-активным, если он осуществляется белками-переносчиками (они ещё называются ионными насосами), источником энергии для которых служат АТР, пирофосфат или субстраты, окисляемые в элек­трон-транспортных цепях митохондрий, хлоропластов.

Типичный пример первично-активного транспорта — активный транспорт ионов с помощью АТФ-аз.

Вторично-активным (сопряженным) транспортом называют процесс переноса ионов через мембрану против градиента его концентрации за счет энергии электро­химического градиента других ионов. Сопряженный транспорт может осуществлять­ся в режиме симпорта (оба иона переносятся через мембрану в одном направлении) или антипорта (ионы транспортируются в противоположных направлениях). Вторич­но-активный транспорт обеспечивает мембранный перенос моносахаридов, сахарозы, аминокислот, пептидов, анионов и ряда катионов. Для этой цели мембранные белки-переносчики чаще всего используют электрохимический градиент ионов водорода, со­здаваемый различными Н+-насосами.

Рис. — Сопряженный транспорт ионов и веществ через мембраны (Δφ — разность потенциалов, ΔрН — разность концентрации протонов)

Между пассивными и активными потоками в клетке существует взаимодействие, направленное на поддержание постоянства ионного состава клетки.

При блокировании энергетики клетки (пониженной температурой, ингибиторами, темнотой) интенсивность активного транспорта снижается, приток ионов из внешней среды уменьшается. Одновременно наблюдается возрастание электрического сопротивления мембраны в десятки раз. Это свидетельствует об уменьшении транспорта ионов по пассивным каналам, что предотвращает потерю ионов, находящихся в клетке.

Видео:Закон диффузии ФикаСкачать

Биологические мембраны. Биоэлектрогенез (лекция 5)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Лекция 5
Биологические мембраны; Биоэлектрогенез
Ростов-на-Дону
2012

Содержание лекции №5
Биологические мембраны и их физические свойства.
Уравнения простой диффузии и электродиффузии. Уравнение Фика. Уравнение Нернста-Планка.
Виды пассивного транспорта.
Понятие об активном транспорте ионов через биологические мембраны.
Потенциал покоя и потенциал действия

и их физические свойства

В каждой клетке есть плазматическая мембрана, которая ограничивает содержимое клетки от наружной среды, и внутренние мембраны, которые формируют различные органоиды
клетки:
митохондрии,
Что есть мозг клетки?
Клетка- мельчайшая структурная единица живого организма
лизосомы
и т.п.

Она состоит из органических молекул, которая имеет толщину 6-10 нм и видима только посредством электронного микроскопа.
Биологическая мембрана (БМ) – это клеточная граница, которой свойственна полупроницаемость.

БМ –это глико – липо — протеидный комплекс
Как понимать полупроницаемость?
Что она дает?
Схема строения клетки , реконструированная по данным электронной микроскопии.
ВОПРОС:

Через биологическую мембрану происходит обмен:
вещество
энергия
клетка
окружающая среда

in
out
БМ – это кожа клетки
in
Клеточные сообщества существуют только благодаря передаче информации от клетки к клетке. Если информационные процессы угнетены
онкозаболевания организм нажимает кнопку на самоуничтожение.
информация

Общие
Механическая
Барьерная
Матричная
Специфические
Транспортная
Рецепторная
Генерация
БП
Принимает участие в
информационных
процессах в живой
клетке
Функции биологических мембран

Структура биологических мембран
БМ = липиды + белки
40%

Из липидной части наиболее важны для структуры фосфолипиды.
Основа фосфолипида – трехатомный
глицерин. К нему присоединяются жирные кислоты.
0,8 нм
1/4
3/4
Полярная часть, где фосфатная группа. «Любит воду». Гидрофильная часть.
Гидрофобная часть. «Хвосты» не любят взаимодействовать с водой.
Физико-химическое свойство фосфолипидов – амфофильность.
Насыщенная жирная кислота
Ненасыщенная жирная кислота

В воде молекулы фосфолипидов автоматически собираются в бислой (bilayer)
Бислой – это
каркас для БМ
Самосборка
Самовосстановление

Мембранные белки (большие глобулы).
На 1 молекулу белка приходится 80-90 молекул фосфилипидов.
Электростатические
взаимодействия
Периферические

Пример: ферменты, рецепторы

Схема расположения молекулы родопсина в биологической мембране (α – спираль, пронизывающая 7 раз фосфолипидный каркас)

Интегральные белки
Периферические белки
Какие белки легче удалить? А для каких нужен детергент?

Схематическое строение БМ

Поверхностные белки
толщина мембраны
Липидный бислой

Различные формы молекулярного движения в БМ
Вращение
Латеральная
диффузия

Перемещение молекул в пределах одной стороны бислоя.
ФЛИП-ФЛОП= перемещение молекул поперек БМ.
Один раз в 2 недели.
В 109 медленнее

Физические свойства БМ
Текучесть ≈ const
Жидкокристаллическая
структура
С = 1 мкФ/см2
БМ — конденсатор
Электросопротивление
105 Ом/см2
гораздо больше, чем у
технических изоляторов
Поверхностный заряд
Отрицательный.
Препятствует слипанию
клеток крови
εлипидов = 2,2
Плотность липидного
бислоя 800 кг/м3 .
Меньше, чем у H2O
Вязкость

η = 100 мПа٠с
(оливковое масло)

Модуль упругости
Е=109 Па

1. Жидкокристаллическая структура
Кристалл
твердый
жидкий

Жидкокристаллическая структура (ЖК)
транспорт
скелет
Фазовый переход при температуре 370 С
Обусловлена необычайно высокой подвижностью мембранных компонентов.
Жидкий кристалл Твердый кристалл
Мембрана сохраняется в ЖК состоянии благодаря температуре клетки и химическому составу жирных кислот.
2. Текучесть ≈ const

3. Вязкость
БМ как ЖК структура характеризуется определенной вязкостью.
η = 100 мПа٠с
(оливковое масло)
На вязкость клеточных мембран влияет содержание в них холестерина.
При повышении содержания холестерина
вязкость . Исчезают
транспортные свойства.
Как влияет?
Бляшки холестерина
в артериях

4. Поверхностный заряд на мембране.
Продуктивность клетки, т.е. ее энергия является измеряемой величиной. Здоровая клетка обладает напряжением 70-90 мВ.
В зависимости от здоровья, напряжение снижается до 20-30 мВ В связи с этим мы чувствуем усталость и изнуренность.
Вся патология на мембранном уровне!

Уменьшение вязкости БМ – причина разжижжения БМ при злокачественных опухолях – при лейкозе.

Вязкость меняется при многих заболеваниях, под действием ионизирующего Э/М излучения , ряда фармпрепаратов.
Вязкость БМ уменьшается при тиреотоксикозе,

а также под действием наркотических веществ, например, хлороформа.

Две стороны мембраны, наружная и внутренняя, различаются и по составу и по функциям.
Эта структурная асимметрия мембран приводит к векторной направленности процессов переноса.
Академик Владимиров Ю.А.

Пассивный транспорт – это перенос веществ через биологическую мембрану без затраты энергии.
Транспорт «под горку»- down hill

Диффузия молекул
Электродиффузия ионов
Уравнение
ФИКА
Уравнение НЕРНСТА -ПЛАНКА
ВИДЫ ПАССИВНОГО ТРАНСПОРТА

Диффузия –это самопроизвольный процесс проникновения массы вещества из области большей концентрации в область с меньшей концентрацией в результате теплового хаотичного движения молекул.
Параметры диффузии

ПЛОТНОСТЬ
ПОТОКА
ВЕЩЕСТВА:

in
out
Уравнения простой диффузии и электродиффузии
Плотность потока
вещества – это количество вещества в единицу времени через единицу площади.

Математическое описание процесса диффузии дал физиолог Фик в 1855 г.

Уравнение Фика является основой конструирования ряда биотехнических систем, например, в аппаратах:
«Искусственная
почка»
Экстракорпорального кровообращения

описывает пассивный транспорт неэлектролитов

C out
C in
C out
C in
in
out
Плотность потока вещества через биологическую мембрану прямо пропорциональна градиенту концентрации
in
D – коэффициент диффузии [м2/с]

Коэффициент диффузии D зависит от природы вещества и температуры и характеризует способность вещества к диффузии.
U=Um NA
U= v/F
D=UmRT
Где — подвижность диффундирующих молекул, выраженная для моля.
Um
Так как
grad C определить трудно, то для описания диффузии веществ через мембрану используют более простое уравнение.
NA
-число Авогадро
R- универсальная газовая постоянная
Т – термодинамическая температура

Уравнение диффузии для мембраны
Где Р- коэффициент проницаемости
in
out
C in
C out
Это более простое уравнение предложено Коллендером и Берлундом.
Плотность потока вещества через биологическую мембрану прямо пропорциональна разности концентраций внутри и снаружи клетки.

Коэффициент проницаемости
C out
C in
где l – толщина БМ
D- коэффициент диффузии
К- коэффициент распределения между липидной и водной фазами.
Р – зависит от температуры, природы вещества, от свойств БМ, ее функционального состояния.
Нет проницаемости мембраны вообще, а есть разная проницаемость БМ для тех или иных веществ.

Уравнения электродиффузии
Перенос ионов
зависит
от двух градиентов
градиента концентрации
grad C
электрического градиента
grad φ.
grad μ
μ

Уравнение Нернста – Планка

Уравнение Нернста – Планка описывает пассивный транспорт ионов

Z – валентность иона
F = 96500 Кл/моль – число Фарадея
C – молярная концентрация
Um – подвижность ионов для моля

Разновидности пассивного транспорта

Простая физическая диффузия (O2, CO2, N2, яды, лекарства).
Через белок-канал (ионы).
Облегченная диффузия
(с носителем).
(АК,моносахариды, глюкоза)

Виды транспорта с носителем
Существуют системы переносчиков, которые
способны транспортировать более одного вещества
μ

out
Понятие об активном транспорте ионов через биологические мембраны
C2=С1
in
C1
Up hill- в горку
Активный транспорт – это перенос веществ (ионов) через БМ, связанный с затратой химической энергии (энергия метаболизма) из области МЕНЬШЕГО ! электрохимического потенциала в область большего электрохимического потенциала.
ВОПРОС: Что будет через некоторое время, если пассивный транспорт?
C1
C2

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Курс добавлен 23.11.2021
• Сейчас обучается 48 человек из 28 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

• Курс добавлен 31.01.2022
• Сейчас обучается 33 человека из 19 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Пассивный транспорт и избирательная проницаемость (видео 7) | Мембранный транспорт | БиологияСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 567 839 материалов в базе

Другие материалы

• 24.12.2020
• 132
• 0

• 03.12.2020
• 69
• 0

• 28.11.2020
• 64
• 0

• 22.11.2020
• 415
• 8

• 16.11.2020
• 137
• 0

• 19.08.2020
• 74
• 0

• 11.08.2020
• 302
• 2

• 10.07.2020
• 94
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 19.08.2020 804
• PPTX 4.7 мбайт
• 5 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Макаренко Наталья Валерьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 22739
• Всего материалов: 225

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:10.1 Закон Фика и уравнение диффузии моноэнергетических нейтронов (часть 1)Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎬 Видео

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Физиология. Потенциал действияСкачать

Уравнения математической физики. Уравнение теплопроводности (диффузии).Скачать

Диффузия и осмос (видео 6) | Мембранный транспорт| БиологияСкачать

Сходство и различия активного и пассивного транспорта через клеточную мембрану. 9 класс.Скачать

[Коллоквиум]: Все, что вы хотели знать про молекулярную биологию, но не удосужились спроситьСкачать

Облегчённая диффузия (видео 8) | Мембранный транспорт | БиологияСкачать

Мембранные потенциалы - Часть 1Скачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Урок 12 (осн). Диффузия. Броуновское движениеСкачать

Химия 9 класс — Как определять Степень Окисления?Скачать

Просто о сложном - ДиффузияСкачать

(АРХИВ) Явления переноса. Мембранный транспортСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Рубин А. Б. - Биофизика I - Мембранный транспорт в клеточных процессахСкачать