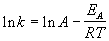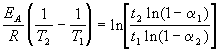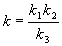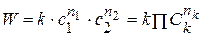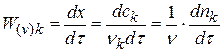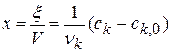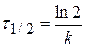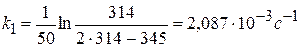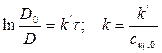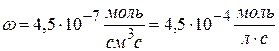Уравнение аррениуса реакция первого порядка

Видео:Лекция 8: уравнение Аррениуса (30.10.2019)Скачать

Уравнение аррениуса реакция первого порядка

Из качественных соображений понятно, что скорость реакций должна увеличиваться с ростом температуры, т.к. при этом возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. Для количественного описания температурных эффектов в химической кинетике используют два основных соотношения — правило Вант-Гоффа и уравнение Аррениуса.

Правило Вант-Гоффа заключается в том, что при нагревании на 10 о С скорость большинства химических реакций увеличивается в 2 4 раза. Математически это означает, что скорость реакции зависит от температуры степенным образом:

, (4.1)

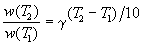
где — температурный коэффициент скорости ( = 24). Правило Вант-Гоффа является весьма грубым и применимо только в очень ограниченном интервале температур.

Гораздо более точным является уравнение Аррениуса, описывающее температурную зависимость константы скорости:

, (4.2)

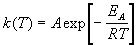
где R — универсальная газовая постоянная; A — предэкспоненциальный множитель, который не зависит от температуры, а определяется только видом реакции; E_A — энергия активации, которую можно охарактеризовать как некоторую пороговую энергию: грубо говоря, если энергия сталкивающихся частиц меньше E_A, то при столкновении реакция не произойдет, если энергия превышает E_A, реакция произойдет. Энергия активации не зависит от температуры.

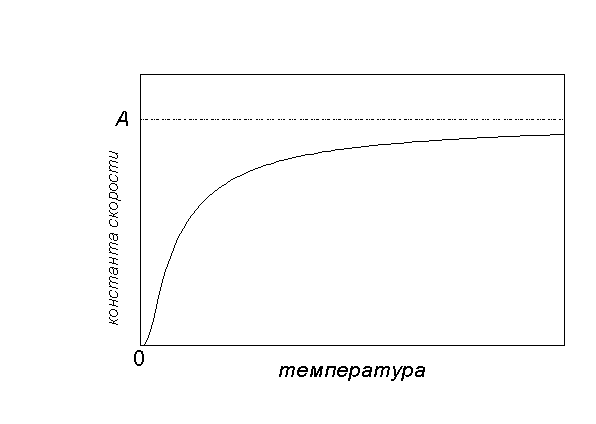
Графически зависимость k(T) выглядит следующим образом:

При низких температурах химические реакции почти не протекают: k(T) 0. При очень высоких температурах константа скорости стремится к предельному значению: k(T) A. Это соответствует тому, что все молекулы являются химически активными и каждое столкновение приводит к реакции.

Энергию активации можно определить, измерив константу скорости при двух температурах. Из уравнения (4.2) следует:

. (4.3)

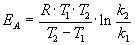
Более точно энергию активации определяют по значениям константы скорости при нескольких температурах. Для этого уравнение Аррениуса (4.2) записывают в логарифмической форме

и записывают экспериментальные данные в координатах ln k — 1/T. Тангенс угла наклона полученной прямой равен —E_A / R.

Для некоторых реакций предэкспоненциальный множитель слабо зависит от температуры. В этом случае определяют так называемую опытную энергию активации:

. (4.4)

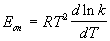
Если предэкспоненциальный множитель — постоянный, то опытная энергия активации равна аррениусовской энергии активации: E_оп = E_A.

Пример 4-1. Пользуясь уравнением Аррениуса, оцените, при каких температурах и энергиях активации справедливо правило Вант-Гоффа.

Решение. Представим правило Вант-Гоффа (4.1) как степенную зависимость константы скорости:

,

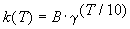
где B — постоянная величина. Сравним это выражение с уравнением Аррениуса (4.2), приняв для температурного коэффициента скорости значение

.

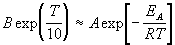
Возьмем натуральный логарифм обеих частей этого приближенного равенства:

.

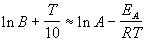
Продифференцировав полученное соотношение по температуре, найдем искомую связь связь между энергией активации и температурой:

.

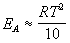
Если энергия активации и температура примерно удовлетворяют этому соотношению, то правилом Вант-Гоффа для оценки влияния температуры на скорость реакции пользоваться можно.

Пример 4-2. Реакция первого порядка при температуре 70 о С завершается на 40% за 60 мин. При какой температуре реакция завершится на 80% за 120 мин, если энергия активации равна 60 кДж/моль?

Решение. Для реакции первого порядка константа скорости выражается через степень превращения следующим образом:

,

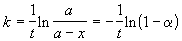
где a = x/a — степень превращения. Запишем это уравнение при двух температурах с учетом уравнения Аррениуса:

,

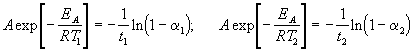
где E_A = 60 кДж/моль, T₁ = 343 K, t₁ = 60 мин, a ₁ = 0.4, t₂ = 120 мин, a ₂ = 0.8. Поделим одно уравнение на другое и прологарифмируем:

Подставляя в это выражение приведенные выше величины, находим T₂ = 333 К = 60 о С.

Пример 4-3. Скорость бактериального гидролиза мышц рыб удваивается при переходе от температуры -1.1 о С к температуре +2.2 о С. Оцените энергию активации этой реакции.

Решение. Увеличение скорости гидролиза в 2 раза обусловлено увеличением константы скорости: k₂ = 2k₁. Энергию активации по отношению констант скорости при двух температурах можно определить из уравнения (4.3) с T₁ = t₁ + 273.15 = 272.05 K, T₂ = t₂ + 273.15 = 275.35 K:

130800 Дж/моль = 130.8 кДж/моль.

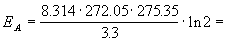
4-1. При помощи правила Вант-Гоффа вычислите, при какой температуре реакция закончится через 15 мин, если при 20 о С на это требуется 2 ч. Температурный коэффициент скорости равен 3.(ответ)

4-2. Время полураспада вещества при 323 К равно 100 мин, а при 353 К — 15 мин. Определите температурный коэффициент скорости.(ответ)

4-3. Какой должна быть энергия активации, чтобы скорость реакции увеличивалась в 3 раза при возрастании температуры на 10 0 С а) при 300 К; б) при 1000 К?(ответ)

4-4. Реакция первого порядка имеет энергию активации 25 ккал/моль и предэкспоненциальный множитель 5 . 10 13 сек -1 . При какой температуре время полураспада для данной реакции составит: а) 1 мин; б) 30 дней?(ответ)

4-5. В каком из двух случаев константа скорости реакции увеличивается в большее число раз: при нагревании от 0 о С до 10 о С или при нагревании от 10 о С до 20 о С? Ответ обоснуйте с помощью уравнения Аррениуса.(ответ)

4-6. Энергия активации некоторой реакции в 1.5 раза больше, чем энергия активации другой реакции. При нагревании от T₁ до T₂ константа скорости второй реакции увеличилась в a раз. Во сколько раз увеличилась константа скорости первой реакции при нагревании от T₁ до T₂?(ответ)

4-7. Константа скорости сложной реакции выражается через константы скорости элементарных стадий следующим образом:

Выразите энергию активации и предэкспоненциальный множитель сложной реакции через соответствующие величины, относящиеся к элементарным стадиям.(ответ)

4-8. В необратимой реакции 1-го порядка за 20 мин при 125 о С степень превращения исходного вещества составила 60%, а при 145 o C такая же степень превращения была достигнута за 5.5 мин. Найдите константы скорости и энергию активации данной реакции .(ответ)

4-9. Реакция 1-го порядка при температуре 25 о С завершается на 30% за 30 мин. При какой температуре реакция завершится на 60% за 40 мин, если энергия активации равна 30 кДж/моль?(ответ)

4-10. Реакция 1-го порядка при температуре 25 о С завершается на 70% за 15 мин. При какой температуре реакция завершится на 50% за 15 мин, если энергия активации равна 50 кДж/моль?(ответ)

4-11. Константа скорости реакции первого порядка равна 4.02 . 10 -4 с -1 при 393 К и 1.98 . 10 -3 с -1 при 413 К. Рассчитайте предэкспоненциальный множитель для этой реакции.(ответ)

4-12. Для реакции H₂ + I₂ 2HI константа скорости при температуре 683 К равна 0,0659 л/(моль. мин), а при температуре 716 К — 0,375 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 700 К.(ответ)

4-13. Для реакции 2N₂O 2N₂ + O₂ константа скорости при температуре 986 К равна 6,72 л/(моль. мин), а при температуре 1165 К — 977,0 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 1053,0 К.(ответ)

4-14. Трихлорацетат-ион в ионизирующих растворителях, содержащих H + , разлагается по уравнению

H + + CCl₃COO — CO₂ + CHCl₃

Стадией, определяющей скорость реакции, является мономолекулярный разрыв связи C- C в трихлорацетат-ионе. Реакция протекает по первому порядку, и константы скорости имеют следующие значения: k = 3.11 . 10 -4 с -1 при 90 о С, k = 7.62 . 10 -5 с -1 при 80 о С. Рассчитайте а) энергию активации, б) константу скорости при 60 о С.(ответ)

4-15. Для реакции CH₃COOC₂H₅ + NaOH ѕ CH₃COONa + C₂H₅OH константа скорости при температуре 282,6 К равна 2,307 л/(моль. мин), а при температуре 318,1 К — 21,65 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 343 К.(ответ)

4-16. Для реакции C₁₂H₂₂O₁₁ + H₂O C₆H₁₂O₆ + C₆H₁₂O₆ константа скорости при температуре 298,2 К равна 0,765 л/(моль. мин), а при температуре 328,2 К — 35,5 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 313,2 К.(ответ)

4-17. Вещество разлагается двумя параллельными путями с константами скорости k₁ и k₂. Какова разность энергий активации этих двух реакций, если при 10 o C k₁/k₂ = 10, а при 40 o C k₁/k₂ = 0.1?(ответ)

4-18. В двух реакциях одинакового порядка разница энергий активации составляет E₂ — E₁ = 40 кДж/моль. При температуре 293 К отношение констант скорости равно k₁/k₂ = 2. При какой температуре константы скорости сравняются?(ответ)

4-19. Разложение ацетондикарбоновой кислоты в водном растворе — реакция первого порядка. Измерены константы скорости этой реакции при разных температурах:

T, о С

k. 10 5 , с -1

Рассчитайте энергию активации и предэкспоненциальный множитель. Чему равен период полураспада при 25 о С? (ответ)

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

Уравнение аррениуса реакция первого порядка

ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ

Конспект лекций для студентов биофака ЮФУ (РГУ)

2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ

2.1.9 Влияние температуры на константу скорости реакции

Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:

При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.

Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:

(II.29)

(II.30)

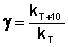
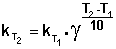
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).

2.1.10 Уравнение Аррениуса

Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.

Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.

Рассмотрим путь некоторой элементарной реакции

Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:

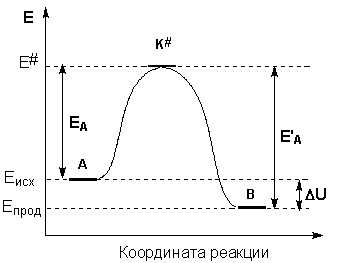
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’_А выше, нежели энергия активации прямой реакции E_A. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).

Рис. 2.5 Энергетическая диаграмма химической реакции.
E_исх – средняя энергия частиц исходных веществ,
E_прод – средняя энергия частиц продуктов реакции

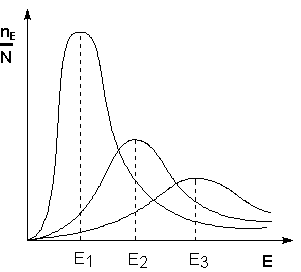
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):

Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
E_i — средняя энергия частиц при температуре T_i (T₁ уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,

(II.31)

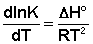
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:

(II.32)

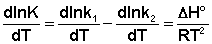
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E₁ и E₂, получаем:

(II.33)

(II.34)

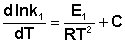
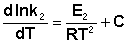
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где E_A – энергия активации :

(II.35)

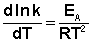
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:

(II.36)

(II.37)

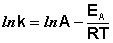
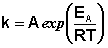
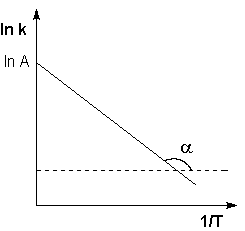
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.

Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации E_A и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).

(II.38)

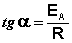
Зная энергию активации реакции и константу скорости при какой-либо температуре T₁, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T₂:

(II.39)

Copyright © С. И. Левченков, 1996 — 2005.

Видео:Уравнение Аррениуса, часть 1Скачать

Тема 2: Реакции первого и второго порядка

НЕРАВНОВЕСНЫЕ ЯВЛЕНИЯ

В СЛОЖНЫХ ХИМИЧЕСИХ ПРОЦЕССАХ

Примеры решения задач

для студентов, обучающихся

по программе бакалавриата по направлению подготовки

240100 – Химическая технология

Тема 1: Кинетика химических реакций.

Реакции первого и второго порядка

Основные расчетные формулы:

;

Глубина протекания химической реакции

Плотность глубины реакции

Реакция I порядка, интегральное уравнение:

;

Реакция II порядка: А+В=С

;

Существует понятие суммарный порядок реакции n = ∑n_k и частный порядок реакции по компоненту

или

Графическое или аналитическое определение Е_а

— система координат при графическом решении уравнения Аррениуса.

Задача № 1

Термическое разложение в газовой фазе (Т = 849 К, V-const)

происходит как одностадийная реакция. Эта стадия является односторонней, мономолекулярной. Рассчитайте константу скорости прямой реакции по следующим данным:

Решение:

1) Для реакции I порядка справедливо интегральное уравнение

;

k должно быть постоянной.

2) Рассмотрим реакцию

Р₀ – исходное давление С₂Н₅СНО. В любой момент времени общее давление пара равно

, тогда

; отсюда

3)

Значение k внесем в таблицу:

4) Вычислим значение k_ср

с -1

Задача № 2

В реакции формальдегида с пероксидом водорода образуется муравьиная кислота (реакция II порядка, )

За время τ = 2 часа при 333,2 К . Вычислите константу скорости реакции; определите время, за которое прореагирует 90% исходных веществ; рассчитайте время, за которое реакции дойдет до той же глубины, если ( ) исходную смесь разбавить в 10 раз.

Дано:

Реакция II порядка

Решение:

Для реакции II порядка при с_1,0=с_2,0

1) =>

2)

3)

Вывод: Если исходные компоненты разбавить в 10 раз, то для достижения той же глубины реакции нужно в 10 раз больше времени.

Задача № 3

Для реакции А→В к = 0,5. Вычислить степень превращения вещества А за время 1 час, если реакция идет по 0, 1 и 2 порядку и с_0,1 = 1 моль/л . Определите, как зависит степень превращения вещества от порядка реакции.

Дано:

Решение:

1) Реакция 0 порядка:

2) Реакция 1 порядка:

;

3) Реакция II порядка

при с_0,1 = С_2,0

Сведем данные расчета в таблицу:

Вывод: При одинаковом значении константы скорости реакции с увеличением порядка реакции уменьшается степень превращения вещества.

Задача № 4

Рассчитать константу скорости реакции кристаллического фиолетового со щелочью по следующим данным

Щелочь берется в избытке: с_щ,0 = 1,8 моль/л, с_кр,0 = 0,01 моль/л, t = 27 0 С.

Решение:

1) Реакция цветная, за концентрацией красителя можно судить по изменению D: D=ε с l

или

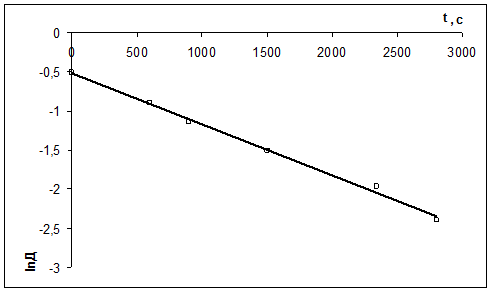
2) Рассчитать k можно графически или аналитическим расчетным способом. Строим график в координатах lnD = f(τ); k ’ = -a = −tgα

2)

Задача № 5

Дана реакция 2 порядка А+В=С. Исходные концентрации с_0,А = с_0,В. За время 500 с реакция проходит на 20%. За какое время она пройдет на 60%?

Решение:

1) Интегральное уравнение реакции II порядка:

; с₀ = 100% = 1, с_τ = 100 — 20 = 80% = 0,8

Ответ: за 3000 с реакция пройдет на 60%.

Тема 2: Реакции первого и второго порядка

Задача № 1

Рассчитайте k, если скорость реакции II порядка равна 4,5∙10 -7 моль/см 3 ∙с при концентрации одного компонента 1,5∙10 -2 моль/л и другого 2,5∙10 -3 моль/л.

Решение:

Ответ: k = 1,2 л/моль∙с

Задача № 2

Определите возраст мумии, если содержание изотопа углерода 14 С в ее тканях составляет 80% от его содержания в живом организме, а период полураспада 14 С равен 5600 лет. Реакция распада углерода относится к реакциям 1 порядка.

Дано:

Решение:

1) Допустим, что с₀ = 1 моль/м 3 , тогда с_τ = 0,8 моль/м 3 .

2) Рассчитываем возраст мумии:

Ответ: возраст мумии 1802 года.

Задача № 3

Реакция взаимодействия уксусного ангидрида с водой является реакцией первого порядка

Дано:

Решение:

1) Рассчитываем k:

2)

3)

4)

Вывод: ко времени полупревращения скорость реакции уменьшается в два раза по сравнению с начальным моментом.

Задача № 4

Превращение перекиси водорода в диэтиловый эфир протекает как реакция I порядка. При 333 К за время 10 мин превращение прошло на 75%. Вычислите константу скорости реакции.

Решение:

Допустим, что с₀ = 1 моль/л, тогда с_τ = с₀ – х = 100-75,2 = 24,8%

Задача № 5

Фенилдиазохлорид разлагается по уравнению:

При 323 К и начальной концентрации 10 г/л были получены следующие результаты:

Рассчитайте константу скорости реакции, постойте график V_N2 = f(τ) и сделайте вывод о порядке реакции.

Решение:

В данной химической реакции за ходом процесса удобно следить по объему выделившегося газа. Реакция мономолекулярная, скорее всего, протекает согласно реакции I порядка. Кинетическое уравнение для реакции I порядка выглядит так:

или

Рассчитаем значение константы:

Значения констант скорости реакции имеет почти одинаковые значения, то это реакция I порядка и взятое нами уравнение удовлетворяет или описывает кинетику этого процесса.

Задача № 6

Найдите время, за которое реакция А→В с константой скорости 6,5∙10 -5 с -1 пройдет а) наполовину; б) на 98%.

Решение:

1) по единице измерения константы можно сказать, что данная реакция относится к реакции I порядка.

2) Кинетическое интегральное уравнение можно записать:

При τ = τ_1/2 с_τ = 0,5с₀, если с₀ = 1 моль/м 3 , то с_τ = 0,5 моль/м 3 .

🔍 Видео

Как температура влияет на скорость химической реакции? Уравнение АррениусаСкачать

Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Порядок реакции и энергия активацииСкачать

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Определение порядка реакции методом подбора кинетического уравненияСкачать

Порядок реакцииСкачать

Использование уравнения Аррениуса для решения задач (2/2). Химия для поступающих.Скачать

Кинетика || Лекция 3 || Реакции первого порядкаСкачать

Скорость реакции. Химия – ПростоСкачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать

Химическая кинетика I. Порядок реакции.Скачать

задачи на порядок хим реакцииСкачать

ЛЕКЦИЯ №12 || Химическая кинетика || Автокатализ, уравнение Аррениуса, энергия активацииСкачать

Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать

Кинетика | Реакции 1-го порядка | Олимпиадные задачи по химииСкачать

5 3 Порядок реакцииСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать