Уравнение бернулли для крыла самолета (2 видео)

Уравнение Бернулли

Чем выше скорость потока идеальной жидкости, тем ниже ее давление.

Вам не приходило в голову, почему самолеты весом несколько сот тонн, разогнавшись, отрываются от взлетно-посадочной полосы и устремляются ввысь? Если нет, то для начала, когда в следующий раз будете в аэропорту, внимательно приглядитесь к разрезу крыла самолета. Прежде всего, обратите внимание, что крыло в разрезе представляет собой сочетание двух выпуклых линий, причем кривизна верхнего контура больше, чем кривизна нижнего, в результате чего площадь верхней поверхности крыла больше площади его нижней поверхности. Именно эта малозаметная для непосвященных деталь конструкции и позволяет самолету отрываться от поверхности земли.

А основополагающая идея здесь такова: воздушный поток разрезается надвое передней кромкой крыла, и часть его обтекает крыло вдоль верхней поверхности, а вторая часть — вдоль нижней. Чтобы двум потокам сомкнуться за задней кромкой крыла, не образуя вакуума, воздух, обтекающий верхнюю поверхность крыла, должен двигаться быстрее относительно самолета, чем воздух, обтекающий нижнюю поверхность, поскольку ему нужно преодолеть большее расстояние. И тут в действие вступает эффект, открытый Даниилом Бернулли, одним из представителей настоящей потомственной династии неутомимых научных гениев родом из Швейцарии. (В авторитетном «Словаре научных биографий», Dictionary of Scientific Biography, упомянуто не меньше восьми представителей фамилии Бернулли.). Отец Даниила — Иоганн Бернулли — был видным профессором математики в Университете г. Гронинген (позже Иоганн Бернулли переехал в Базель и возглавил кафедру греческого языка местного университета, однако после смерти брата вернулся в Гронинген, чтобы сменить его на посту заведующего кафедрой математики. Книга Даниила «Гидродинамика» (Hydrodynamica) была опубликована в 1738 году, практически одновременно с книгой Иоганна Бернулли «Гидравлика» (Hydraulica), которая по взаимной договоренности между сыном и отцом была, однако, специально датирована 1732 годом, чтобы, в случае чего, в семье не возникло недоразумений относительно приоритетов в открытиях. Вот такая семья!).

Объединив законы механики Ньютона с законом сохранения энергии (см. Первое начало термодинамики) и условием неразрывности жидкости, Даниил Бернулли смог вывести уравнение, согласно которому давление со стороны текучей среды падает с увеличением скорости потока этой среды (понятие «текучая среда» включает жидкость или газ). В случае с самолетом воздух обтекает крыло самолета снизу медленнее, чем сверху. И благодаря этому эффекту обратной зависимости давления от скорости давление воздуха снизу, направленное вверх, оказывается больше давления сверху, напрвленного вниз. В результате, по мере набора самолетом скорости, возрастает направленная вверх разность давлений, и на крылья самолета действует нарастающая по мере разгона подъемная сила. Как только она начинает превышать силу гравитационного притяжения самолета к земле, самолет в буквальном смысле взмывает в небо. Эта же сила удерживает самолет в горизонтальном полете: на крейсерской скорости и высоте подъемная сила уравновешивает силу тяжести.

Если вы часто летаете самолетом, вы не могли не заметить и еще одного явления, напрямую связанного с эффектом Бернулли. Самолет в аэропорту вашего родного города в разные дни берет разгон по взлетно-посадочной полосе в противоположных направлениях, и садится на нее также то в одном, то в другом направлении. Выбор направления не произволен: он зависит от направления ветра. При движении навстречу преобладающему ветру скорость воздушного потока, обтекающего крыло самолета, равна скорости самолета относительно земли плюс скорость самого ветра относительно земли. Поэтому при движении навстречу ветру, скорость отрыва от земли, при которой подъемная сила, описываемая уравнением Бернулли, начинает превышать силу тяжести, оказывается ниже, и самолету требуется меньшая длина разбега или торможения после посадки. Тем самым снижается риск выхода за пределы взлетно-посадочной полосы и экономится горючее за счет того, что часть подъемной силы создается за счет энергии встречного ветра.

С эффектом Бернулли вы можете встретиться также, когда сидите ненастным вечером дома у камина. Во время особенно сильных порывов ветра языки пламени взмывают вверх, в дымоход. А происходит следующее: когда скорость ветра у выходного отверстия трубы возрастает, давление в этом месте падает. Более высокое давление внутри дома буквально «выталкивает» пламя из камина в дымоход. Вы, наверное, замечали спиральные лопатки вокруг выходных отверстий заводских труб. Они установлены там с той же целью: направляя ветер вокруг и над отверстием трубы, они способствуют белее эффективному выбросу отработанных газов.

Сам я использую эффект Бернулли весьма неожиданным образом. Для поддержания физической формы я у себя в Вашингтоне регулярно совершаю пробежки на роликовых коньках по специальной заасфальтированной дорожке, идущей вдоль реки Потомак. На трек я выхожу неподалеку от Национального аэропорта, и, еще паркуя свою машину, я первым делом смотрю, в каком направлении взлетают или приземляются авиалайнеры. Если они садятся или взлетают в том направлении, куда я собираюсь прокатиться, значит, всё в порядке, и на обратном пути мне будет помогать попутный ветер. Если же они садятся мне навстречу, значит, дистанцию пробежки лучше сократить, поскольку на обратном пути ветер будет дуть мне в лицо, а я этого не люблю. Тем самым эффект Бернулли позволяет мне точно дозировать ежедневные физические нагрузки.

Швейцарский математик, физик и физиолог. Родился в Гронингене (Нидерланды) в семье потомственных математиков и интеллектуалов. Первоначально получил медицинское образование, и в 1725 году принял приглашение Петербургской академии наук и занял пост профессора кафедры физиологии. Обнаружив в этой области множество нерешенных задач из области теоретической физики и, в частности, динамики движения жидкости (крови) в сосудах, вернулся к математическому описанию физических процессов и в 1730 году возглавил кафедру чистой математики Петербургской академии. В 1733 году вернулся на родину в Базель, где возглавил кафедру анатомии и ботаники местного университета, а с 1750 года — кафедру экспериментальной физики, которой и руководил до своей смерти. В результате изучения гидродинамических зависимостей сформулировал так называемый принцип Бернулли и на столетие предвосхитил зарождение молекулярно-кинетической теории газов.

Содержание

Возникновение аэродинамической силы на крыле
Элементы гидро- и аэродинамики
Элементы гидродинамики. Уравнение Бернулли
Элементы аэродинамики
📸 Видео

Видео:Урок 135. Применения ур-ния Бернулли (ч.2). Подъемная сила крыла самолета (ч.1)Скачать

Возникновение аэродинамической силы на крыле

Тема 1. ОСНОВЫ ТЕОРИИ ПОЛЕТА

Принцип полета самолета, вертолета

Основы аэродинамики самолета

Аэродинамика – это наука, изучающая законы движения воздуха (газа) и исследующая взаимодействие воздушного потока с телом, которое оно обтекает.

При обтекании воздушным потоком на поверхности летательных аппаратов возникают аэродинамические силы и моменты, которые определяют их летно-технические характеристики.

Основные законы аэродинамики:

1. Закон постоянства расхода воздуха (уравнение неразрывности), который основан на законе сохранения материи (материя вечна, она не создается из ничего и не исчезает бесследно). Он гласит, что при установившемся движении газа его массовый секундный расход постоянен во всех сечениях:

G_в – секундный расход воздуха;

ρ – плотность воздуха;

f – площадь сечения струйки;

V – скорость воздуха в сечении.

Для дозвуковых скоростей ρ= const и уравнение неразрывности примет вид:

Из уравнения видно, что если площадь поперечного сечения потока газа уменьшается, то скорость течения в это же число раз увеличивается (и наоборот).

2. Закон постоянства энергии воздуха (газа) в потоке (закон Бернулли) устанавливает связь между скоростью движения воздуха и давлением в нем. Он является частным случаем закона сохранения энергии (энергия не исчезает бесследно и не возникает из ничего, а может только переходить из одного вида в другой). Он гласит, что полная энергия потока воздуха при отсутствии обмена энергией с окружающей средой есть величина постоянная и для дозвуковых скоростей имеет вид:

p – давление воздуха в соответствующих сечениях (определяет потенциальную энергию, запасенную в газе);

ρ V 2 /2 – скоростной напор воздуха (определяет кинетическую энергию газа).

Иначе говоря, сумма статического давления в потоке и скоростного напора есть величина постоянная. Отсюда следует важный вывод, что при увеличении скорости потока воздуха давление в нем уменьшается и наоборот.

Закон Бернулли объясняет возникновение аэродинамических сил на крыле самолета и несущем винте вертолета.

Возникновение аэродинамической силы на крыле

Рассмотрим картину обтекания крыла самолета потоком воздуха (см. рис. 1.1)

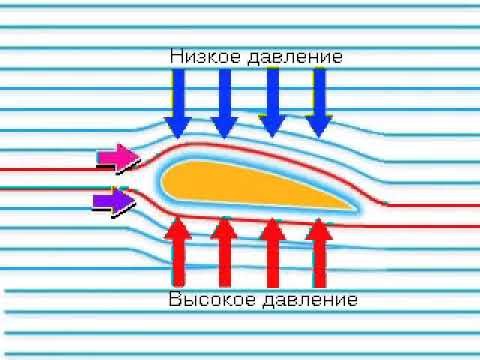
Поток воздуха обтекает верхнюю и нижнюю части профиля крыла неодинаково. Струйки воздуха над крылом проходят путь больший, чем под крылом (вследствие большей кривизны верхней части профиля крыла). Исходя из закона неразрывности газового потока, скорость воздуха над крылом получается больше, чем под ним. В соответствии с законом Бернулли над крылом давление воздуха падает, а под крылом растет.

Так возникает аэродинамическая подъемная сила Y, направленная вверх. В горизонтальном установившемся полете подъемная сила равна силе веса воздушного судна G. Кроме того на крыло и летательный аппарат в целом воздействует сила сопротивления воздуха X, направленная назад по полету. Для преодоления этой силы сопротивления и поступательного движения самолета вперед необходима сила тяги R, которая создается силовой установкой ВС.

Сила тяги силовой установки необходима для разгона самолета до скорости, при которой на крыле возникнет подъемная сила, превышающая вес самолета.

Подъемная сила крыла зависит от формы профиля крыла, очертания крыла в плане,

Основные геометрические характеристики крыла:

— профиль крыла – форма поперечного сечения крыла;

— хорда профиля (b) – условная прямая линия, соединяющая переднюю и заднюю точки профиля;

— угол атаки (α) – угол, образованный хордой крыла и направлением набегающего потока воздуха;

— средняя аэродинамическая хорда крыла (САХ) – хорда условного прямоугольного крыла такой же площади, которое при равных углах атаки имеет одинаковые с данным крылом величину полной аэродинамической силы и положение центра давления.

При увеличении угла атаки подъемная сила крыла растет, но до определенного момента, после чего она резко падает. Угол атаки, при котором значение подъемной силы достигает максимальной величины, называется критическим углом атаки.

Резкое падение подъемной силы после достижения критического угла атаки объясняется нарушением плавности обтекания крыла потоком воздуха: на верхней поверхности крыла образуется сильное вихреобразование со срывом струй воздуха.

Критические углы атаки для современных гражданских самолетов лежат в пределах 16-18º. На углах атаки, близких к критическим, устойчивость и управляемость самолета резко ухудшаются, поэтому полеты на таких углах атаки не должны производиться.

Видео:Как летает самолет? Закон Бернулли - Основы авиации #2Скачать

Элементы гидро- и аэродинамики

Для того, чтобы описать такой сложный процесс, как движение жидкостей или газов, применяют разного рода упрощенные модели. Например, для упрощения используется предположение, что жидкость или даже газ несжимаемы и идеальны, не имеют внутреннее трение между слоями, которые движутся. Когда такая идеальная жидкость находится в движении, отсутствует переход механической энергии во внутреннюю, т.е. имеет место выполнение закона сохранения механической энергии. В свою очередь, из этого закона для стационарного потока идеальной и несжимаемой жидкости вытекает уравнение (принцип) Бернулли, которое было сформулировано в 1738 г.

Видео:Подъёмная сила крыла ● 1Скачать

Элементы гидродинамики. Уравнение Бернулли

Стационарный поток жидкости – это поток без образования вихрей. В этом случае частицы жидкости осуществляют перемещение по постоянным во времени траекториям, называемым линиями тока.

В рамках имеющегося опыта можно утверждать, что возникновение стационарных потоков возможно лишь тогда, когда скорость движения жидкости достаточно мала.

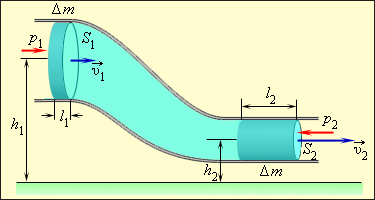
Возьмем для рассмотрения стационарное течение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1 . 22 . 1 ). Различные части трубы располагаются на разных высотах.

Рис. 1 . 22 . 1 . Поток идеальной жидкости в трубе переменного сечения.

Рассматриваемая труба имеет два сечения: S 1 и S 2 ; Δ t — это время прохождения жидкости в трубе. Так, за Δ t через сечение S 1 жидкость осуществит перемещение на l 1 = υ 1 Δ t ; через сечение S 2 – на l 2 = υ 2 Δ t ( υ 1 и υ 2 – обозначение скоростей частиц жидкости в трубе соответствующих сечений). Условие несжимаемости будет иметь следующую запись: Δ V = l 1 S 1 = l 2 S 2 или υ 1 S 1 = υ 1 S 1 , где Δ V является объемом жидкости, прошедшей через сечения S 1 и S 2 .

С переходом жидкости из участка трубы большего сечения в участок меньшего сечения скорость движения потока увеличивается: жидкость перемещается с ускорением. Это означает, что жидкость испытывает воздействие силы. Если речь идет о движении потока в горизонтальной трубе, можно утверждать, что возникновение этой силы возможно только как следствие разности давления в широком и узком участках трубы (в широком участке давление должно быть больше, чем в узком). В случае же, когда различные участки трубы располагаются на разной высоте, ускорение потока обусловлено совокупным воздействием силы тяжести и силы давления.

Сила давления есть упругая сила сжатия жидкости.

Явление несжимаемости жидкости означает только то, что возникновение упругих сил имеет место при пренебрежимо малом изменении объема любой части жидкости.

Поскольку действует предположение, что жидкость идеальна, ее протекание по трубе происходит без трения, а значит к ее движению уместно применять закон сохранения механической энергии.

В процессе движения жидкости силы давления выполняют работу, которую запишем так:

Δ A = p 1 S 1 l 1 – p 2 S 2 l 2 = p 1 S 1 υ 1 Δ t — p 2 S 2 υ 2 Δ t = ( p 1 – p 2 ) Δ V .

Работа Δ A сил давления есть изменение потенциальной энергии упругой деформации жидкости, взятое с обратным знаком.

Те изменения, которые происходят за промежуток времени Δ t в выделенной части жидкости, помещенной между участками трубы с сечениями S 1 и S 2 в начальный момент времени, в случае стационарного течения заключаются в перемещении массы жидкости Δ m = ρ Δ V из участка с сечением S 1 в участок сечением S 2 ( ρ – плотность жидкости). На рисунке 1 . 22 . 1 соответствующие объемы обозначены штриховкой. Закон сохранения механической энергии для этой массы будет иметь запись: E 2 – E 1 = Δ A = ( p 1 – p 2 ) Δ V . E 1 и E 2 здесь являются полными механическими энергиями массы Δ m в поле тяготения и записываются так:

E 1 = ∆ m v 1 2 2 + ∆ m g h 1 ; E 2 = ∆ m v 2 2 2 + ∆ m g h 2 .

Откуда можно вывести:

p v 1 2 2 + p g h 1 + p 1 = p v 2 2 2 + p g h 2 + p 2 .

Выражение p v 1 2 2 + p g h 1 + p 1 = p v 2 2 2 + p g h 2 + p 2 называется уравнением Бернулли.

Из уравнения Бернулли следует, что: p v 2 2 + p g h + p = c o n s t на всей протяженности рассматриваемой трубы. В частном случае, когда труба расположена горизонтально, уравнение Бернулли принимает вид: p v 2 2 + p = c o n s t .

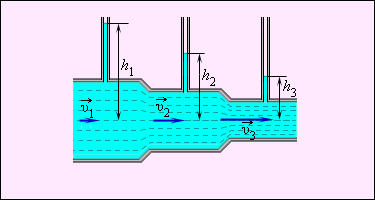
Величина p обозначает статическое давление в жидкости, которое возможно измерить, используя манометр, двигающийся вместе с жидкостью. В практике давление в различных сечениях трубы определяют при помощи манометрических трубок, размещаемых через боковые стенки в поток жидкости таким образом, чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 1 . 22 . 2 ). Из уравнения Бернулли следует:

Давление в жидкости, проходящей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в коих скорость больше.

Рис. 1 . 22 . 2 . Использование манометров для определения давления в потоке.

В случае, когда сечение потока жидкости достаточно велико, уравнение Бернулли необходимо применять к линиям тока, т. е. линиям, вдоль которых происходит перемещение частиц жидкости при стационарном течении.

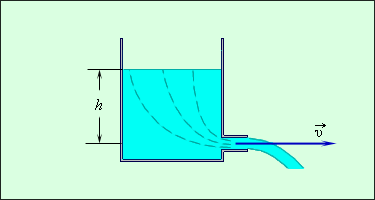
Мы имеем широкий сосуд с отверстием в боковой стенке, в котором течет идеальная несжимаемая жидкость. При движении потока из отверстия линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 1 . 22 . 3 ).

Рис. 1 . 22 . 3 . Истечение жидкости из широкого сосуда.

Так как скорость жидкости вблизи поверхности в широком сосуде является пренебрежимо малой, уравнение Бернулли примет вид: p v 2 2 + p = c o n s t ,

где p 0 – атмосферное давление, h – перепад высоты вдоль линии тока. Тогда: v = 2 g h .

v = 2 g h — это формула, выражающая скорость истечения потока и называемая формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Элементы аэродинамики

Отличительной чертой газов от жидкостей является возможность значимо изменять свой объем. Расчеты позволяют утверждать, что сжимаемостью газов можно пренебречь, когда наибольшие скорости в потоке являются малыми по сравнению со скоростью звука в этом газе. Следовательно, уравнение Бернулли возможно использовать для достаточно широкого класса задач аэродинамики.

В числе подобных задач — исследование сил, осуществляющих воздействие на крыло самолета. Строго теоретически решить эту задачу достаточно затруднительно, и обычно для изучения сил используют экспериментальные методы. Уравнение Бернулли дает возможность только качественно объяснить появление подъемной силы крыла.

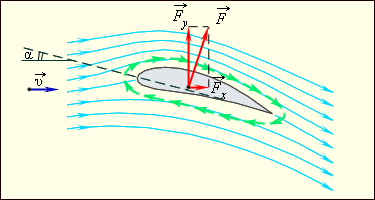
Рис. 1 . 22 . 4 демонстрирует линии тока воздуха, обтекающего крыло самолета. Особый профиль крыла и наличие угла атаки (угла наклона крыла по отношению к набегающему потоку воздуха) определяют тот факт, что скорость течения воздуха над крылом становится больше, чем под крылом. В связи с этим на рис. 1 . 22 . 4 линии тока над крылом расположены ближе друг к другу, чем под крылом. Выводом из принципа Бернулли является то, что давление в нижней части крыла будет больше, чем в верхней, и в итоге мы имеем силу F → , осуществляющую действие на крыло.

F y → – вертикальная составляющая силы F → , называемая подъемной силой.

F x → — горизонтальная составляющая силы F → , называемая силой сопротивления среды.

Подъемная сила дает возможность компенсации силы тяжести, осуществляющей действие на самолет, и этим она и определяет саму возможность движения тяжелых летательных аппаратов в воздушной среде.

Рис. 1 . 22 . 4 . Линии тока при обтекании крыла самолета и возникновение подъемной силы. α – угол атаки.

Теорию подъемной силы крыла самолета сформулировал Н. Е. Жуковский в 1904 г., и она получила название теоремы Жуковского:

Подъёмная сила сегмента крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Направление действия подъёмной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции.

Жуковский продемонстрировал, что при обтекании крыла значимое влияние оказывают силы вязкого трения в поверхностном слое. Итогом их воздействия является возникновение кругового движения или циркуляции воздуха вокруг крыла (обозначено стрелками зеленого цвета на рис. 1 . 22 . 4 ). В верхней части крыла скорость циркулирующего воздуха соединяется со скоростью набегающего потока, в нижней же части эти скорости противоположно направлены. Подобный эффект и служит причиной появления разности давлений и образования подъемной силы.

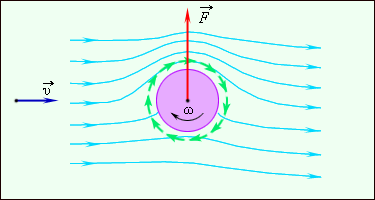
Циркуляция воздуха, определяемая силами вязкого трения, появляется и вокруг тела, которое вращается. Практически значимым, к примеру, является вращение цилиндра.

При вращении цилиндра само тело влечет за собой примыкающие слои воздуха, создавая циркуляцию воздушного потока. Когда цилиндр установлен в набегающем потоке, возникает сила бокового давления, подобная подъемной силе крыла самолета. Такое явление носит название эффекта Магнуса.

На рис. 1 . 22 . 5 проиллюстрировано обтекание цилиндра, осуществляющего вращение, набегающим потоком. Примером эффекта Магнуса служит полет закрученного мяча при игре в теннис или футбол.

Рис. 1 . 22 . 5 . Обтекание вращающегося цилиндра набегающим потоком воздуха.

Таким образом, на множество явлений аэродинамики оказывают значимое влияние силы вязкого трения. Они дают толчок к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не берет в расчет силы трения. Вывод Бернулли опирается на закон сохранения механической энергии при течении жидкости или газа. Поэтому при помощи принципа Бернулли невозможно исчерпывающе объяснить явления, в которых имеется проявление сил трения. В подобных случаях возможно опираться лишь на качественные соображения – чем больше скорость, тем меньше давление в потоке газа.

Особо заметное проявление имеют силы вязкого трения в потоке жидкостей. Некоторые жидкости обладают вязкостью такой значимой величины, что использование уравнения Бернулли может привести к качественно неверным результатам.

К примеру, в случае истечения жидкости высокой вязкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше той, что будет рассчитана по формуле Торричелли. Когда сферическое тело движется в идеальной жидкости, оно не должно встречать лобового сопротивления. Когда такое тело перемещается в вязкой жидкости, появляется сила сопротивления, и ее модуль будет пропорционален скорости υ и радиусу сферы r (закон Стокса) F с о п р

Коэффициент пропорциональности в этом выражении имеет зависимость от свойств жидкости. Т.е., если шарик значимого веса бросить в высокий сосуд, содержащий вязкую жидкость (к примеру, глицерин), то спустя некоторое время скорость шарика установится на уровне определенного значения, не изменяющегося при последующем движении шарика. Когда движение будет происходить на некой установившейся скорости, силы, влияющие на шарик (сила тяжести m g → , выталкивающая сила F А → и сила сопротивления среды F с о п р ), оказываются скомпенсированными, и их равнодействующая будет равна нулю.