Уравнение баланса энергии электромагнитного поля в вещественной форме и его физическое содержание (4 видео)

Тема 4. баланс энергии ЭМП

Плотность ЭМ энергии и энергия, сосредоточенная в объеме. Мощность тепловых потерь и сторонних источников. Уравнение баланса для мгновенных значений мощности в дифференциальной и интегральной форме (теорема Умова – Пойнтинга). Физическая трактовка. Мощность, выходящая и входящая из объема через замкнутую поверхность. Вектор Пойнтинга. Мощность на входе приемника. Вектор Пойнтинга изотропного источника.

Средние за период значения энергетических характеристик гармонического ЭМП. Теорема Умова – Пойнтинга для комплексных мощностей. Комплексный вектор Пойнтинга. Уравнения баланса для активных и реактивных мощностей. Физическая трактовка. Скорость переноса энергии ЭМП.

Указания к теме

Поскольку ЭМ форма движения материи подчиняется закону сохранения энергии, непосредственно из системы уравнений Максвелла следует уравнение баланса энергии ЭМП (теорема Умова – Пойнтинга).

Необходимо учесть, что источником ЭМП является сторонняя сила, которую поддерживают посторонние по отношению к исследуемому полю источники. Сторонние источники не зависят от исследуемого поля и вводятся в основные уравнения ЭМП в виде дополнительных слагаемых.

При изучении этой темы важно уяснить физическое содержание каждого слагаемого уравнений баланса энергии как для некоторой области, так и для любой точки пространства. Необходимо рассмотреть различные виды балансов энергии (пассивный, нейтральный, активный) на примере LC-контура, чтобы уяснить связь между вектором Пойнтинга и движением энергии, ее излучением или поглощением, притоком или оттоком, скоростью движения энергии.

При изучении гармонических полей нужно обратить внимание на средние за период энергетические характеристики ЭМП, физическое содержание вещественной и мнимой частей вектора Пойнтинга.

Необходимо уяснить связь вектора Пойнтинга с мощностью, принимаемой антенной в дальней зоне приема, а также понять, почему плотность потока энергии изотропного источника убывает при удалении от него даже при отсутствии потерь в пространстве.

Основные сведения

После преобразования уравнений (2.5)–(2.8) [1–6] получаем дифференциальнуюформу теоремы Умова – Пойнтинга

. (4.1)

После интегрирования по объему (4.1) и преобразований получаем

. (4.2)

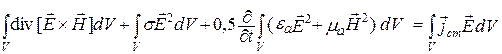
Каждое слагаемое в выражении (4.2) имеет размерность мощности

. (4.3)

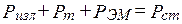
Уравнения (4.2)–(4.3) позволяют сформулировать теорему Умова –Пойнтинга: «Мощность стороннего источника в данном объеме расходуется на излучение, тепловые потери и изменение запаса энергии ЭМП» [1–3].

Мощность тепловых потерь (потерь проводимости) подчиняется закону Дж. Джоуля – Э. Ленца. Изменение запаса энергии имеет размерность мощности :

, (4.4)

Вектор называется вектором Пойнтинга. По теореме Остроградского – Гаусса [1–3] .

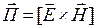
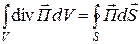
Вектор Пойнтинга указывает направление распространения излучения, а его модуль представляет собой плотность потока мощностиизлучения.

В комплексной форме уравнения (4.2) и (4.3) имеют вид [1]

; (4.5)

, (4.6)

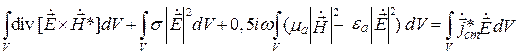
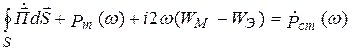
где ; ; ,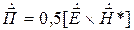

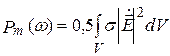
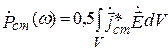
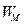
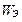
а и – энергия магнитного и электрического полей соответственно.

Выражение (4.6) – баланс комплексных мощностей в объеме V.

Рассмотрим баланс ЭМ энергии (4.3) в контуре, представляющем замкнутую электрическую цепь из элементов с сосредоточенными параметрами (рис. 4.1).

Энергия стороннего источника расходуется на тепловые потери, которые сосредоточены в активном сопротивлении R_т, на изменение запаса ЭМ энергии в контуре (электрическая энергия накапливается в емкости C, а магнитная – в индуктивности L), на излучение из контура (элемент взаимной индуктивности М_ik с другим контуром и «излучающий конденсатор» – электрический вибратор.

Выделим действительную и мнимую части уравнения (4.6)

; (4.7)

. (4.8)

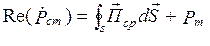
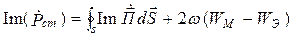
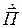
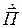
Действительная часть характеризует перенос энергии через граничную поверхность области V в окрестности точки наблюдения, а мнимая часть – колебание энергии через ту же поверхность [1, 12].

Из выражения (4.7) следует, что средняя мощность стороннего источника тратится на тепловые потери в объеме V и на создание ЭМП за пределами V.

Из выражения (4.8) следует, что реактивная мощность стороннего источника расходуется на создание потока реактивной мощности через границу V и на создание запаса реактивной энергии в объеме V. Реактивная мощность характеризует процесс обмена энергией между источником и цепью. При P_р > 0 энергия запасается в магнитном поле, а при P_р

Дата добавления: 2018-09-24 ; просмотров: 2009 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Уравнение баланса мгновенных значений мощности
Энергия электромагнитного поля
Рекомендуемые материалы
📹 Видео

Видео:3.4 Уравнения баланса мощностей в монохроматическом полеСкачать

Уравнение баланса мгновенных значений мощности

Как уже отмечалось в 1.1, электромагнитное поле является одной из форм материи. Как и любая другая форма материи, оно обладает энергией. Эта энергия может распространяться в пространстве и преобразовываться в другие формы энергии.

Сформулируем уравнение баланса для мгновенных значений мощности применительно к некоторому объему V, ограниченному поверхностью S (рис. 1.23). Пусть в объеме V, заполненном однородной изотропной средой, находятся сторонние источники. Из общих физических представлений очевидно, что мощность, выделяемая сторонними источниками, может расходоваться на джоулевы потери и на изменение энергии электромагнитного поля внутри V, а также может частично рассеиваться, уходя в окружающее пространство через поверхность S. При этом должно выполняться равенство

, (1.120)

где Рст – мощность сторонних источников;

Рп – мощность джоулевых потерь внутри объема V;

– мощность, проходящая через поверхность S;

W– энергия электромагнитного поля, сосредоточенного в объеме V, adW/dt– мощность, расходуемая на изменение энергии в объеме V.

Рис. 1.23. Объем V, ограниченный поверхностью S

В данном разделе будут использованы уравнения состояния (1.53). Эти уравнения не позволяют учесть потери энергии при поляризации и намагничивании среды. Поэтому слагаемое Рпв равенстве (1.120) фактически определяет мощность джоулевых потерь в объеме V, обусловленных током проводимости.

Уравнение (1.120) дает только качественное представление об энергетических соотношениях. Чтобы получить количественные соотношения, нужно воспользоваться уравнениями Максвелла. Рассмотрим первое уравнение Максвелла с учетом сторонних токов (1.111). Все члены этого уравнения – векторные величины, имеющие размерность А/м2.

Чтобы получить уравнение, аналогичное (1.120), нужно видоизменить первое уравнение Максвелла (1.111) так, чтобы его члены стали скалярными величинами, измеряющимися в ваттах. Для этого достаточно все члены указанного равенства скалярно умножить на вектор Е, а затем проинтегрировать полученное выражение по объему V. После скалярного умножения на вектор Е получаем

(1.121)

Используя известную из векторного анализа формулу div[E,H]= Н rot Е – Е rot H, преобразуем левую часть соотношения (1.121) и заменим rot E его значением из второго уравнения Максвелла (1.39):

Подставляя это выражение в (1.121), получаем

(1.122)

В последнем слагаемом в правой части (1.122) изменен порядок сомножителей в скалярном произведении векторов и Н. Это допустимо, так как . Данное изменение не является принципиальным и не дает никаких преимуществ при выводе рассматриваемого здесь уравнения баланса для мгновенных значений мощности. Однако при такой записи во всех членах уравнения (1.122) второй сомножитель (векторы jст, j, и Н) является вектором, входившим ранее в первое уравнение Максвелла. Это обстоятельство позволит в дальнейшем (см. 1.8.4) несколько упростить вывод уравнения баланса в случае монохроматического поля (уравнения баланса комплексной мощности). Интегрируя почленно уравнение (1.122) по объему V, получаем

(1.123)

где направление элемента dSсовпадает с направлением внешней нормали к поверхности S. При переходе от (1.122) к (1.123) использована теорема Остроградского – Гаусса для перевода объемного интеграла от div [Е, Н] в поверхностный интеграл от векторного произведения [Е, Н]. Введем обозначение

и преобразуем подынтегральное выражение в последнем слагаемом в правой части (1.123):

(1.125)

Подставляя (1.124) и (1.125) в (1.123) и меняя порядок интегрирования и дифференцирования, получаем

. (1.126)

Выясним физический смысл выражений, входящих в уравнение (1.126).

Рассмотрим первое слагаемое в правой части (1.126). Представим объем Vввиде суммы бесконечно малых цилиндров длиной dl, торцы которых (dS) перпендикулярны направлению тока (вектору j). Тогда EjdV= EjdV= (Edl)(jdS) = dUdl= dPп, где dl=jdS– ток, протекающий по рассматриваемому бесконечно малому цилиндру; dU= Edl– изменение потенциала на длине dl, adPп – мощность джоулевых потерь в объеме dV. Следовательно, рассматриваемое слагаемое представляет собой мощность джоулевых потерь Рп в объеме V. Используя соотношение j = σЕ, для Рп можно получить и другие представления:

(1.127)

Формулы (1.127) можно рассматривать как обобщенный закон Джоуля-Ленца (П. 33), справедливый для проводящего объема Vпроизвольной формы.

Интеграл в левой части (1.126) отличается от первого слагаемого в правой части только тем, что в подынтегральное выражение вместо j входит jст. Поэтому он должен определять мощность сторонних источников. Будем считать положительной мощность, отдаваемую сторонними токами электромагнитному полю. Электрический ток представляет собой упорядоченное движение заряженных частиц. Положительным направлением тока считается направление движения положительных зарядов. Ток отдает энергию электромагнитному полю при торможении образующих его заряженных частиц. Для этого необходимо, чтобы вектор напряженности электрического поля Е имел составляющую, ориентированную противоположно направлению тока, т.е. чтобы скалярное произведение векторов Е и jст было отрицательным (Ejст Будет полезно почитать по теме:

Видео:Урок 287. Индуктивность контура (катушки). Явление самоиндукцииСкачать

Энергия электромагнитного поля

Раздел 4 Энергия электромагнитного поля.

4.1. Баланс энергий электромагнитного поля.

Как и любая форма материи, электромагнитное поле обладает энергией, которая может распространяться в пространстве и преобразоваться в другие виды энергии.

Сформулируем уравнение баланса электромагнитного поля применительно к некоторому объему V, ограниченному поверхностью S. Пусть, в этом объеме, за счет сторонних источников, выделяется электромагнитная энергия. Из общефизических соображений, очевидно, что мощность сторонних источников будет расходоваться на потери, на изменение энергии и частично будет рассеиваться на поверхности S, уходя во внешнее пространство.

Будем полагать, что среда в объеме V однородная и изотропная. Мощность в объеме V выделяется за счет протекания сторонних токов, в дальнейшем будем пользоваться известными материальными уравнениями:

(1)

; ; (2)

Материальные уравнения в форме (2) не позволяют учесть потери связанные с явлением поляризации и намагничивания вещества. Уравнение баланса в форме (1) дает качественное представление о балансе энергии. Для получения уравнения необходимо перейти к векторам электромагнитного поля, т.е. воспользоваться уравнениями Максвелла. Для получения количественного соотношения обратимся к уравнениям Максвелла.

Видео:Билет №38 "Поток энергии"Скачать

Рекомендуемые материалы

Запишем первое уравнение Максвелла с учетом сторонних токов:

(3)

Размерность входящих в (3) составляющих . Они являются векторными величинами.

Для получения уравнения, аналогичного (1), надо уравнение (3) преобразовать в скалярное и обеспечить размерность слагаемых в Ваттах. Указанный алгоритм можно реализовать, если каждое из слагаемых умножить скалярно на и проинтегрировать по объему.

Умножим все составляющие на Е, получим:

(4)

Преобразовав левую часть (4) используем известное векторное тождество:. Из полученного тождества вытекает следующее выражение: (5)

Выразим, используя второе уравнение Максвелла:

; (6)

Подставляя правую часть (6) в левую часть (4) получим:

(7)

Преобразуем предыдущее выражение следующим образом:

Также (7) можно записать следующим образом:

(8)

(9)

В последнем соотношении (9) мы сделаем следующее:

1) поменяем порядок дифференцирования по времени, и интегрирования по объему.

2) При интегрировании по объему воспользуемся теоремой Остроградского — Гаусса.

Для цилиндрического проводника с током I: .

Для элементарного цилиндрического проводника, концы которого перпендикулярны линиям тока:

(10)

Для произвольного объема:

(11)

В выражении (11) первый интеграл это мощность потерь.

В левой части (9) стоит мощность, выделяемая сторонними токами в объеме V. Ток проводимости, который представляет собой упорядоченное движение заряженных частиц, отдает энергию электромагнитного поля, если частицы попадают в тормозящее электромагнитное поле.

Для того, чтобы электромагнитное поле было тормозящим необходимо чтобы скалярное произведение удовлетворяло следующему условию: .

При этом левая часть (9) становится положительной величиной.

Рассмотрим второе слагаемое правой части. Будем полагать, что поверхность S окружающая V является идеально проводящей

и проводимость среды в объеме равна нулю.

, , ,

По условию поверхность S является идеально проводящей.

При этом уравнение баланса имеет следующий вид:

(12)

т.е. в рассматриваемом случае мощность сторонних источников может расходоваться на изменение энергии внутри объема. В правой части выражения (12) мы получили скорость изменения энергии .

(13)

в V=>

(14)

В этом случае мощность сторонних токов рассеиваясь на поверхности S уходит во внешнее пространство. Таким образом, мы получили, что уравнение (9) полностью идентично формуле (1).

Соотношение (9) было сформулировано Поинтингом (уравнение баланса энергии электромагнитного поля – теорема Пойнтинга).

Проанализируем несколько частных случаев,

которые следуют из теоремы Пойнтинга.

1.Энергия может поступать в объем V не только за счет сторонних источников. Поток энергии, определяемой интегралом , может быть направлен из внешнего пространства внутрь объема V.

2. Сторонние источники могут не только отдавать энергию, а также вбирать энергию электромагнитного поля. Поток заряженных частиц вбирает энергию электромагнитного поля, если этот поток попадает в ускоряющее электрическое поле. При этом скалярное произведение , а левая часть в соотношении (9) становится отрицательной величиной.

3. Пусть, поток энергии, определяемой последним слагаемым в соотношении (9), направлен внутрь объема, причем, мощность, которая поступает, таким образом, расходуется на джоулевы потери и вбирается сторонним источником так, что энергия внутри объема V остается неизменной. В этом случае соотношение (9) преобразуется к виду (15)

(15)

Так как слева стоит полная поступающая через поверхность энергия, то вектор можно трактовать как плотность потока энергии (вектор Пойнтинга).

Вектор Пойнтинга равняется пределу отношения энергии, проходящей за время DТ, через поверхность DS, перпендикулярно направлению распространения энергии, при DS и DТ стремящихся к нулю. В изотропных средах направление совпадает с направлением распространения энергии.

4.2. Плотность энергии электромагнитного поля.

Из предыдущего параграфа известно, что запас электромагнитного поля в объеме V: (1)

Правую часть можно представить в виде двух слагаемых, одно из которых зависит только от электрического поля, а другое только от магнитного.

; (2)

Так как энергии представлены в виде интегралов по объему, то подынтегральные выражения можно трактовать как объемную плотность энергий, а их сумму — как объемную плотность энергии электромагнитного поля.

; (3)

(4)

Принцип суперпозиции, которому удовлетворяют векторы электромагнитного поля, не распространяется на энергию электромагнитного поля.

Пусть в объеме V существует независимо два электромагнитных поля. Энергия суммарного электромагнитного поля:

(5)

где W₁₂ — взаимная энергия электромагнитного поля. Она может быть как положительной, так и отрицательной, т.е. суммирование электромагнитных полей может приводить как к увеличению энергии результирующего поля, так и к уменьшению ее. Если электрический и магнитный вектора, суммируемых полей, взаимно ортогональны, то очевидно, что взаимная энергия будет равна нулю. В случае переменных процессов электромагнитная энергия непрерывно изменяется. Эти изменения в каждой точке можно описать следующим соотношением:

(6)

Так как левая часть и первое слагаемое есть подынтегральные выражения, то их можно трактовать объемной плотностью мощности сторонних источников и сторонних потерь.

(7)

(8)

Соотношение (8) есть дифференциальная форма теоремы Пойнтинга.

4.3. Скорость распространения энергии электромагнитных волн.

В пространстве, в котором распространяется электромагнитная энергия, выделим энергетическую трубку (некий протяжный объем, на боковой поверхности которого вектор Пойнтинга равен нулю).

Пусть, за время Dt через боковую поверхность DS прошла энергия DW и оказалась сосредоточенной между сечениями DS и DS₁ , между которыми, расстояние Dl. Направление единичного вектора совпадает с направлением распространения энергии.

Тогда скорость распространения энергии:

(1)

Энергию, заключенную между торцами DS и DS₁:

(2),

где w — объемная плотность энергии, а DS ’ — среднее сечение.

Если промежуток Dt взять достаточно малым, чтобы не успел измениться, то энергию:

(3)

Приравняем (2) к (3) и выразим . Получим:

(4)

Найдем предел от соотношения (4) при Dt®0. Получим:

(5)

Получили общее выражение для величины скорости распространения энергии. Если предположить, что векторы и , а стало быть, и неизменны в пределах поперечного сечения цилиндра, то в этом случае, векторы и совпадают по направлению распространения энергии.

(6)

4.4. Уравнения Максвелла для монохроматического поля.

4. Метод комплексных амплитуд.

Любые переменные электромагнитные процессы можно представить в виде дискретного или непрерывного спектра гармонических электромагнитных полей. Поэтому в дальнейшем будем анализировать гармонические электромагнитные процессы (монохроматические), так как сигнал любой сложности можно представить как суперпозицию гармонических процессов. Обычно используют метод комплексных амплитуд.

Пусть имеется некоторый гармонический процесс:

(1),

ему в соответствие ставится: (2)

(3)

Аналогично и для векторных величин. Пусть, есть вектор изменяющийся по гармоническому закону:

(4)

Ему соответствует комплексная величина:

(5)

или

(6)

Если, мгновенные скалярные и векторные функции удовлетворяют некоторым линейным уравнениям, то этим же уравнениям удовлетворяют и их комплексные аналоги.

Использование метода комплексных амплитуд существенно упрощает решение задач с геометрическими электромагнитными процессами. Причина этого: дифференцирование по времени от комплексных амплитуд эквивалентно просто домножению на jw, а интегрирование по времени эквивалентно делению на jw.

5. 4.5. Система уравнений монохроматического (гармонического) поля.

Известно, что уравнения Максвелла относятся к линейным дифференциальным уравнениям. Поэтому в случае гармонических электромагнитных полей в уравнениях Максвелла можно перейти к комплексным амплитудам.

Т.е. если , то , где

Используя понятие комплексных амплитуд, получим:

(1) т.к. , (2)

(3)

(4), где (5)

— комплексная диэлектрическая проницаемость среды.

Входящее в соотношение (5) отношение называется тангенсом угла электрических потерь: (6)

Комплексная диэлектрическая проницаемость в форме (5) справедлива для сред, в которых имеются только джоулевы потери. В общем случае, когда необходимо учесть диэлектрические потери представляется в следующем виде: (7)

(8) – тангенс угла диэлектрических потерь

Этот общий случай позволяет также учесть потери, связанные с эффектом поляризации в переменном электрическом поле. Наличие диэлектрических потерь приводит к появлению фазового сдвига между электрическими векторами D и Е. Величина которого: (9)

Переходя во втором уравнении Максвелла к комплексным амплитудам получим: (10).

, где (11)

(12) — тангенс угла магнитных потерь.

Магнитные потери связаны с эффектом периодического изменения намагниченности вещества во внешнем поле. Наличие магнитных потерь приводит к фазовому запаздыванию вектора В относительно вектора Н (явление Гистерезиса) в электромагнитных средах.

В случае гармонического поля при использовании метода комплексных амплитуд, возникает дополнительная возможность учесть потери, связанные с эффектами поляризации и намагничивания вещества.

В случае гармонических полей при использовании метода комплексных амплитуд 3 и 4 уравнения Максвелла являются следствием первых двух.

В средах с проводимостью неравной нулю объемная плотность убывает и в случае установившегося электромагнитного процесса (к ним относятся гармонические колебания). Можно считать, что объемная плотность электрического заряда равна нулю. В этом случае третье уравнение Максвелла запишется следующим образом:

(13)

Это соотношение для среды с конечной проводимостью. Оно является справедливым и для не проводящих сред. Если в непроводящей среде рассмотрим гармонический процесс, то:

Всякое изменение свободных электрических зарядов сопровождается появлением в среде электрического тока, но при в среде невозможно появление тока удовлетворяющего закону Ома. Поэтому (13) является справедливым в случае гармонических процессов и для непроводящих сред.

Переходя в уравнении (13) к комплексным амплитудам, получим:

(14)

Покажем, что оно является следствием (4). Возьмем дивергенцию от правой и левой части. Аналогично и для 4 уравнения Максвелла:

(15)

В случае гармонических полей они полностью описываются соотношениями(4), (11). Будем предполагать, что в рассмотренной области имеются сторонние источники. В этом случае выражения (4), (11) не применимы. Для получения справедливых соотношений воспользуемся 1 уравнением Максвелла:

(16)

(17)

Рассмотрим 3 уравнение Максвелла. Возьмем дивергенцию от соотношения (16).

Для сторонних токов:

Окончательно получим: (18)

В случае гармонических электромагнитных полей мы должны воспользоваться соотношением (17) и (18), при этом (4) и (11) останутся без изменений.

Итак, когда имеются сторонние источники:

Уравнения Максвелла без учета сторонних источников:

Подставляя вторую систему в первую, с использованием метода комплексных амплитуд, получим:

В дальнейшем индекс m будем формально опускать.

5.6. Уравнения баланса для средней за период мощности.

Теорема Умова-Пойнтинга и соответствующее ей аналитическое соотношение

(1)

были сформулированы для мгновенных значений и остаются справедливыми в последний момент времени. Это соотношение — важнейшее в классе электродинамики.

При анализе гармонических электромагнитных процессов особый интерес представляют энергетические параметры, усредненные по периоду. Среднее за период значение: (2)

Получим уравнение баланса для средней за период значения мощности гармонического электромагнитного процесса. Необходимо для каждого из слагаемых уравнения (1) получить величину, определяемую соотношением (2). Т. к. в соотношении (2) осуществляется интегрирование по времени, а анализируется гармонический электромагнитных процесс, то, естественно, надо воспользоваться методом комплексных амплитуд. Непосредственная замена мгновенных функций, соответствующими комплексными аналогами возможна только в линейных уравнениях. В данном случае непосредственная замена мгновенных векторов электромагнитного поля невозможна, так как выполняются следующие неравенства:

В случае нелинейных уравнений, переход к комплексным амплитудам осуществляют с помощью следующего соотношения:

(3)

Получим уравнение баланса для средней за период значения мощности гармонического электромагнитного поля. Сначала определим среднее за период значения функций входящие в (1).

Для начала получим среднее за период значение вектора Пойнтинга:

раскроем векторное произведение: (4)

Таким образом, сумму можно записать как удвоенную действительную часть любого из слагаемых:

(5)

Величина от времени не зависит. С учетом приведенных рассуждений, получаем:

(6)

Подставим (6) в (2). Два последних слагаемых, в соотношении (6), меняются с удвоенной частотой, т.е. половину периода принимают положительную величину, а другую половину — отрицательную. Поэтому и среднее за период значение равно нулю.

(7)

Величина, от которой берется действительная часть (8) называется комплексным вектором Пойнтинга.

(8) — комплексный вектор Пойнтинга.

(9)

Итак, (7) определяет среднее за период значение плотности потока энергии через поверхность S. Среднее за период значение потока мощности:

(10)

Рассмотрим каждое из слагаемых выражения (1).

(11)

(12)

(13)

(14)

Таким образом, в результате проделанных нами вычислений, получили:

(15)

(16)

В среднем за период, мощность сторонних источников расходуется на потери внутри объема и частично уходит во внешнее пространство, через поверхность S.

6. 4.7. Уравнения баланса для комплексной мощности.

В радиотехнике часто пользуются понятием комплексной мощности. Так, если рассматривается гармонический процесс, то комплексную мощность сторонних источников можно записать:

Получим уравнение баланса для комплексных мощностей гармонического электромагнитного процесса. Уравнение баланса для комплексной мощности получается аналогично уравнению баланса для среднего за период значения. Удобно записать уравнение Максвелла сразу для комплексно-сопряженных величин:

(1)

Вновь полагаем, что потери в среде обусловлены конечной проводимостью:

Возьмем комплексное сопряжение от всех комплексных величин:

(2)

Умножим скалярно правую и левую части соотношения (1) на . Получим:

(3)

Воспользуемся векторным тождеством, из которого следует:

Выразим из тождества :

, тогда:

Будем предполагать, что магнитные потери в среде отсутствуют, тогда . Подставим в соотношение (3): (4)

7. Проинтегрируем по объему:

(5)

Поделим на 2 и учтем, что во втором слагаемом стоит разность энергий

(6)

(7)

Выражение (7) запишем в виде системы из 2-х уравнений: одно устанавливает связь между активными мощностями, другое — между реактивными.

Получим: (8)

(9)

Как мы и ожидали, соотношение (8) совпадает с уравнением для средних за период мощностей. Из (9) следует, что реактивная мощность сторонних источников равна умноженной на 2w разности средних за период значений энергий + реактивный поток энергии, через поверхность S. Рассмотрим важное приложение к (8) и (9). Будем предполагать, что объем V, для которого составлено уравнение баланса, является изолированной системой. В этом случае комплексный поток мощности, через поверхность S, равен нулю и уравнение баланса:

(10)

В этом случае происходит колебательный обмен энергией между электрическим и магнитным полями, т.е. один момент существует только электрическое поле, потом и то и другое, потом только магнитное и т.д. В том случае когда

(11)

мощность сторонних источников становится чисто активной:

(12)

и обмен энергиями происходит без участия сторонних источников. Если (11) не соблюдается, то для этого обмена необходимо участие сторонних источников. Изолированная система, в которой мощность сторонних источников чисто активна, т.е. выполняется равенство (11), называется резонирующей изолированной системой, а условие (11) называется условием резонанса. Для характеристики изолированной колебательной системы вводят понятие добротности.

Под добротностью Q понимают:

(13)

(14)

Средняя за период энергия электрического поля:

При резонансе , тогда

Соотношения (6), (7) были получены при условии, что . Потери в среде обусловлены конечной проводимостью

В этом случае общее выражение для баланса комплексных мощностей остается неизменным, но конкретное, аналитическое выражение для слагаемых, изменится. Мощность потерь записывается следующим образом:

В заключение этого параграфа приведем выражение для скорости распределения энергии, записанное через комплексные амплитуды:

, где DS — поперечное сечение.

В том случае, когда составляющие неизменны, получаем:

8. 4.8. Теорема единственности для внутренней и внешней задач электродинамики.

Уравнения Максвелла являются дифференциальными уравнениями в частных производных, поэтому они допускают множество решений. Из общефизических соображений, очевидно, что если полностью повторять условия опытов, то будем получать одно и то же распространение электромагнитного поля. Для обеспечения единственности решения электродинамических задач электромагнитное поле должно удовлетворять не только уравнениям Максвелла, но также должно удовлетворять ряду дополнительных условий. Они называются условиями единственности решения уравнений Максвелла. Выводы и доказательства формулируются теоремой единственности. Теорема единственности отдельно формулируется двух основных видов задач:

для внутренней и внешней задач электродинамики.

Требуется определить распределение электромагнитного поля внутри поверхности S (внутренняя задача). Определим распространение электромагнитного поля в пространстве, внешнем по отношению к объему V, ограниченному поверхностью S. ().

9. 4.9. Единственность решения внутренних задач.

Внутренние задачи электродинамики имеют единственное решение, если выполняется одно из следующих условий:

1.Если в каждой точке М поверхности S задана проекция вектора на плоскость, касательную к поверхности S в точке М: — «Е» задача.

2. Если в каждой точке M поверхности S задана проекция вектора на плоскость, касательную к поверхности S в точке М: — «Н» задача.

3. Если на части поверхности S в каждой точке задана проекция вектора на плоскость, касательную к S в этой точке, а на другой части плоскости задана проекция вектора касательная к S в точке М:

— «ЕН» задача.

4. Если в каждой точке поверхности S задано соотношение между проекциями векторов и на плоскость, касательную к S в точке М.

10. 4.10. Условия единственности внешних задач электродинамики.

Для обеспечения единственности решения внешних задач электродинамики необходимо выполнение одного из условий 1-4, плюс к этому должно выполнятся одно из условий, описывающее поведение электромагнитного поля при бесконечно удаленных точках (при r®¥).

1. Принцип предельного поглощения () требует, чтобы эта зависимость была , т.е. каждая из составляющих поля должна убывать с увеличением расстояния быстрее, чем . В реальных средах имеются пусть очень малые, но конечные по величине потери, т.е. . Поэтому, в бесконечно удаленных точках, электромагнитное поле равно нулю.

2. Если в среде отсутствуют потери и принцип предельного поглощения не применим, в этом случае векторы электромагнитного поля должны удовлетворять следующим соотношениям:

— условия Зоммерфельда.