Теоретическая интерпретация зависимости вязкостей жидкостей от температуры составляет неотъемлемую часть теории вязкости и теории жидкого состояния в целом. Разработка этой теории позволяет проникнуть в механизм вязкого течения и вскрыть природу вязкости и одновременно вывести обоснованные уравнения зависимости вязкости от температуры.
Промежуточное положение жидкостей между газами и твердыми телами позволяет развивать теорию жидкого состояния, отправляясь или от молекулярно-кинетической теории газов или от теории твердого состояния. В пользу сближения жидкостей с газами говорят непрерывный переход одного состояния в другое (испарение и конденсация) и сходство многих законов гидро- и аэромеханики. С другой стороны, теплоемкость и плотность жидкостей мало отличаются от плотности и теплоемкости твердых тел, откуда следует, что расстояние между молекулами в обоих этих состояниях одного порядка. Межмолекулярными силами взаимодействия жидкостей нельзя пренебрегать, как это делают в классической молекулярно-кинетической теории газов.
Егер пытался объяснить вязкость жидкостей тем, что в результате молекулярно-кинетического движения молекулы переносятся из одного слоя жидкости в другой. Вследствие этого во время течения возникает стремление выровнять скорости сдвига в слоях, что воспринимается как внутреннее трение. Так как с повышением температуры перенос молекул возрастает, то из теории Егера следует, что вязкость должна повышаться с увеличением температуры. Для газов такая зависимость действительно наблюдается, но вязкость жидкостей падает с увеличением температуры. Непосредственное применение представлений о переносе движения молекул газов для объяснения поведения жидкостей приводит к результатам, противоречащим опыту. Тем не менее молекулярно-кинетическая теория газов была плодотворно использована А. Д. Гольдгаммером и некоторыми другими авторами при выводе уравнения А. И. Бачинского . Н. Герасимов считает, что теория вязкости жидкостей должна базироваться на теории реальных газов .
Я. И. Френкель развивает кинетическую теорию жидкости, исходя из сходства жидкостей с твердыми телами . В ceoefr теории вязкости жидкостей он принимает, что движение молекул жидкостей подобно молекулам твердого тела сводится преимущественно к колебаниям около положения равновесия. Текучесть жидкости объясняется тем, что положения равновесия могут скачкообразно перемещаться. Средняя продолжительность колебания молекул около одного положения равновесия зависит от температуры согласно уравнению
где т — период колебания; к — постоянная Больцмана; —энергия, которую необходимо сообщить частице для перехода из одного состояния равновесия в другое (энергия активации вязкого течения).
Процесс перемещения точек равновесия рассматривается как диффузия. Пользуясь уравнением Стокса, связывающим вязкость с трением, и уравнением Эйнштейна, связывающим трение с коэ-фициентом диффузии, Я. И. Френкель из уравнения (IV, 3) выводит следующее уравнение:
где А — постоянная.
где V — удельный объем; Л—постоянная, пропорциональная частоте колебаний молекул; С—постоянная, пропорциональная потенциальной энергии.
В развитии теории вязкости значительную роль сыграла подсобная гипотеза о пустых ультрамикрополостях (дырках) в жидкости, имеющих молекулярные размеры. Согласно этой гипотезе течение жидкости представляет собой процесс перемещения молекул в эти пустоты. Исходя из молекулярно-кинетических представлений, Я. И. Френкель вычислил энергию образования таких полостей, а Эйринг и Юелл определили энергию испарения молекул в дырки.
Многие современные теории жидкого состояния принимают, что в жидкости существует два порядка взаимодействия молекул: ближний, соответствующий твердому телу, и дальний —соответствующий газам. С. Э. Хайкин и В. И. Данилов исходили из представления о том, что в жидкости сохраняются агрегаты молекул с кристаллической структурой.
Экспоненциальная зависимость вязкости от температуры, впервые выведенная теоретическим путем Я. И. Френкелем, получила в настоящее время широкое признание. Экспоненциальные уравнения из различных представлений о течении были получены Эйрин-гом и Юеллом, Панченковым , Раманом и др. Сводка этих уравнений с обширной библиографией составлена М. П. Воларовичем 1.
Для химиков особый интерес представляет связь температурной зависимости вязкости с составом и молекулярной структурой жидкостей. Г. М. Панченков , Берналл , Уард и другие пытались ввести в уравнения вязкости размеры молекул или координационное число, определяющее количество ближайших соседей рассматриваемой молекулы, и некоторые другие физико-химические свойства. Обращалось внимание на то, что в уравнение Андраде необходимо вводить поправку, связанную с симметричностью молекул. Было показано, что, как правило, в гомологических рядах отношение вязкости при температуре застывания к вязкости при температуре кипения тем больше, чем менее симметрична молекула.
Бернал и Уард полагают, что энергия активации в уравнениях типа (IV, 4) соответствует температуре плавления. Еще раньше к аналогичному заключению пришел Я. И. Френкель . Ниссан, Кларк и Нэш в соответствии с теорией Эйринга и Юелла считают, что энергия активации ближе связана с теплотой парообразования. Свои представления они развивают на примерах реальных жидкостей, в том числе углеводородов
Я. И. Френкель отмечает, что вязкое течение молекулярных, особенно высокомолекулярных, жидкостей обладает другим механизмом, чем течение простых атомных жидкостей (ртуть, сжиженные инертные газы). Он приходит к выводу, что общий объем ультрамикропустот таких жидкостей обратно пропорционален объему отдельных молекул, а так как текучесть жидкости согласно его теории является функцией возможности перемещения молекул в эти пустоты, то вязкость должна быть прямо пропорциональна молекулярному объему. Выше было указано, что обширный экспериментальный материал по вязкости жидкостей различного состава приводит к аналогичному заключению.
Теория жидкого состояния находится в начальной стадии своего развития. Она еще не в состоянии сколько-нибудь детально учесть индивидуальные особенности химического состава и строения жидкостей. Все теории вязкости, предложенные до настоящего времени, не учитывают ассоциации молекул жидкостей. По этой причине разработанные экспоненциальные уравнения применяют только к наиболее простым, неассоциированным жидкостям. Для таких жидкостей уравнение А. И. Бачинского является наиболее широко применимым законом температурной зависимости вязкости. В этой связи А. С. Предводителев, М. Ф. Широков и А. Д. Гольдгаммер предложили различные теоретические обоснования этого уравнения. Я. И. Френкель пытался согласовать выведенную им экспоненциальную зависимость с уравнением А. И. Бачинского.
Так как подавляющее большинство продуктов переработки нефти является ассоциированными жидкостями и их вязкость в очень сильной степени зависит от химического состава, практическое значение теоретических уравнений для вычисления вязкости нефтепродуктов ограничено. Для этой цели применяют почти исключительно эмпирические уравнения.
Видео:ТФКП. Проверить условия Коши-Римана. Выяснить является ли функция аналитической.Скачать

Влияние температуры на вязкость расплавов и растворов полимеров. Энергия активации вязкого течения
Вязкость – свойство оказывать сопротивление необратимому изменению формы образца. Большинство экспериментальных методов измерения h сводится к независимому определению в опыте напряжений сдвига t и скоростей деформации j и установлению функции течения j = f(t). Величина эффективной вязкости полимеров hэф определяется как отношение величин t/j, зависящее от значений t и j, полученных по результатам измерений на капиллярных или ротационных вискозиметрах. Размерность hэф в системе СИ – нс/м2, в системе СГС – пуаз (пз). 1 пз = 0,1 нс/м2. Вязкость типичных расплавов полимеров лежит в диапазоне: для ПА, ПЭТФ – 102 пз; для ПЭ, ПП, ПС – 104-106 пз; для несшитых каучуков – 109 пз. В полимергомологическом ряду вязкость может изменяться в очень широких пределах. В промышленности выпускаются полиэтилены, h которых различается более чем в 200 раз из-за неодинаковой молекулярной массы. На практике вязкость легко регулируется изменением температуры, например, h расплава ПЭ снижается почти в 10 раз при повышении температуры на 60-80°.
Температурная зависимость вязкости существенно влияет на технологические свойства расплавов полимеров, определяет выбор режимов переработки, качество изделий и требования к контрольно-регулирующей аппаратуре.
Элементарный акт процесса течения состоит в преодолении молекулярно-кинетической единицей (МКЕ) потенциального барьера при переходе из одного положения в другое. Для этого ей необходимо обладать достаточной энергией и, кроме того, вблизи исходного положения равновесия должно существовать свободное пространство – «дырка», которой может отвечать новое равновесное положение МКЕ. Второе требование связано с условием одновременного изменения равновесных положений нескольких МКЕ. В таком случае течение становится кооперативным процессом. В теории Эйринга нахождение h(Т) сводится к определению числа возможных переходов МКЕ через потенциальный барьер при различных температурах. Общие методы теории абсолютных скоростей приводят к следующему выражению вязкости жидкости:
Поскольку мольный объем V изменяется с температурой слабо, а величину энтропии DS* принимают независящей от температуры, уравнение можно переписать в виде

(1)
(Формула Аррениуса — Френкеля — Эйринга: АФЭ),
где Е – энергия активации процесса; В – постоянная.
Поскольку В, хотя и слабо, но все же зависит от Т, более точным для описания h(Т) является выражение

. (2)
Учет множителя Т2/3 дает незначительное уточнение по сравнению с экспоненциальным членом формулы (2).
Видео:Фазовые кривые.Скачать

Уравнение аррениуса френкеля эйринга описывающее зависимость вязкости от температуры имеет вид
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.9 Влияние температуры на константу скорости реакции
Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:
При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.
Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:
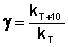
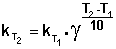
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).
2.1.10 Уравнение Аррениуса
Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.
Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.
Рассмотрим путь некоторой элементарной реакции
Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:
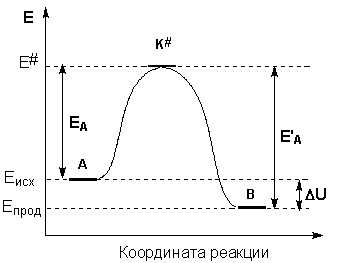
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).
Рис. 2.5 Энергетическая диаграмма химической реакции.
Eисх – средняя энергия частиц исходных веществ,
Eпрод – средняя энергия частиц продуктов реакции
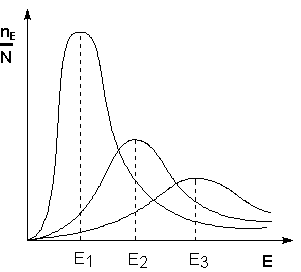
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
Ei — средняя энергия частиц при температуре Ti (T1 уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,
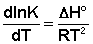
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
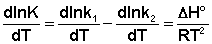
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
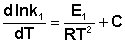
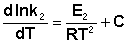
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации :
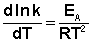
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
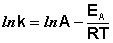
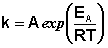
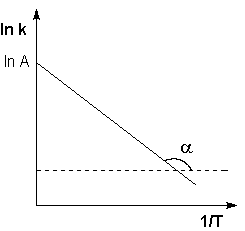
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.
Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).
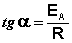
Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2:
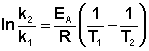
Copyright © С. И. Левченков, 1996 — 2005.
📹 Видео
Закон Харди-Вайнберга - наглядное объяснение | Закон генетического равновесияСкачать

Математика для всех. Алексей Савватеев. Лекция 2.5. Леонард Эйлер - историческая справкаСкачать

Увеличение альтернативных издержекСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Кривая ФиллипсаСкачать

Сложение КПВ (3 способа), альтернативные издержкиСкачать

ТФКП. Восстановление функции по действительной части u(x,y). Условия Коши-Римана. Формула Эйлера.Скачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

1.4 Ограниченность и выбор Альтернативные издержкиСкачать

АиСД S03E09. Строки. Хеширование. КМПСкачать

АиСД S03E12. Суффиксное дерево. Алгоритм УкконенаСкачать

Инфимум, супремум, нижний и верхний пределы последовательности ★ Демидович 101.1Скачать

История экономической мысли #4 ФизиократыСкачать

Гемайншафт Тённиса и органическая солидарность Дюркгейма | Олимпиады по обществознанию | мейнкурсСкачать

A.7.24 Так что же меняет аффинное преобразование?Скачать

АиСД S04E07. Задача о назначениях. Венгерский алгоритмСкачать

Характеристическое рентгеновское излучениеСкачать