Разделы: Математика
Цели урока:
- Повторение основных приемов преобразования и методов решения логарифмических уравнений; акцентирование внимания учащихся на возможных ошибках в решении логарифмических уравнений.
- Расширение знаний темы “Логарифмические уравнения” посредством знакомства с уравнениями, содержащими знак модуля.
- Развитие познавательных способностей посредством содержания и формы проведения урока, развития вариативного мышления, развития общеучебных навыков, работа с книгой, с компьютером.
- Развитие коммуникативных навыков, развитие монологической речи, умение критически мыслить, отстаивать свою точку зрения.
- Организация на урок /5 минут/.
- Повторение теоретического материала по теме “ Равносильные уравнения. Решение логарифмических уравнений”:
а) устная работа (просмотр презентаций, обсуждение теоретических вопросов) / 7–8 минут/;
б) диктант с последующей проверкой /5–7 минут/. - Работа учащихся с карточками (нахождение ошибок) (самостоятельно), обсуждение решений уравнений /10-12 минут/.
- Совместная работа учащихся и учителя (решение уравнений в тетрадях и у доски) /10 минут/.
- Подготовка к экзаменам:
а) разбор уравнений, решения которых заранее подготовлены учителем для просмотра через плазменный экран и решаемого учеником /15 минут/;
б) самостоятельная работа учащихся (по карточкам разного уровня сложности) /20минут/. - Итог урока, выставление оценок /2 минуты/.
I этап урока — организационный
Учитель сообщает учащимся тему урока, цель и добавляет, что во время урока они будут пользоваться раздаточным материалом, находящимся на партах.
II. Повторение теоретического материала по теме: “ Равносильные уравнения. Решение логарифмических уравнений”
Для того, чтобы решать логарифмические уравнения, следует повторить необходимые для этого теоретические сведения:
Выступление I ученика
Приложение 1 показ слайдов демонстрационной презентации с четкими формулировками:
- слайд №1-определение равносильных уравнений;
- слайд № 2 – определение уравнения следствия;
- слайд № 3 – область допустимых значений уравнения
- слайд №4- что понимают под логарифмическим уравнением;
Диктант (с последующей взаимопроверкой)
Возможные ответы: “+”-да , “-” — нет
| Вариант 1 | Вариант 2 |
| Верно ли утверждение: | Верно ли утверждение: |
| Если 4 х =7, то х=log47 |
Если log525=x, то х=2
Если log381=x, то х=4
lgxlg5=3 и lg(x+5)=3
lg
lgx+lg(x 3 -1)= 2 и lg(x(x 3 -1))=2

Выступление II ученика
Приложение2 показ слайдов демонстрационной презентации с основными видами логарифмических уравнений:
- слайд №1–
;
- слайд №2 –
;
- слайд №3 – в уравнении логарифмы с разными основаниями;
- слайд №4–
;
- слайд №5– метод введения новой переменной.
1. Укажите промежуток, которому принадлежит больший корень уравнения ln(х — 5) 2 = 0.
2. Найдите произведение корней уравнения 1- lg(x 2 +1) = 0.
3. Укажите промежуток, которому принадлежат корни уравнения log0,5(x — 9) = 1 + log0,55.
4. Укажите промежуток, которому принадлежит корень уравнения log4(x — 5) = log255.
Задание 1 2 3 4 Номер ответа 4 2 1 2
III. Работа учащихся с карточками. Объяснение ошибок
Учащимся на отдельных листах предлагаются уравнения с решениями, содержащими ошибки. Необходимо обнаружить эти ошибки, объяснить их и выполнить решение предложенных уравнений правильно (допускается решение уравнения иным способом после обнаружения ошибки в приведенном варианте решения).
Обсуждение решения уравнений
В задаче 1 для преобразования выражения 






Видео:ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать

В задаче 2 при преобразовании выражения log3 (x + 4) 2 пропущен знак модуля.
В задаче 3 преобразование дроби 
В задаче 4 при преобразовании основания логарифма был поставлен знак модуля, однако, поскольку показатель степеней нечетный, то такое преобразование привело к расширению множества решений (-2 — посторонний корень для исходного уравнения).
В решении задачи 5 нарушено условие монотонности соответствующей функции (если f— монотонная функция и а ЄDf, bЄ Df, то f (a) = f(b) а = b) .
IV. Решение уравнений
Этот этап урока может быть организован различно: учащиеся выполняют самостоятельно решение уравнений с последующей проверкой, кто-то из учащихся показывает решение на доске и пр.
V. Подготовка к экзаменам
а) разбор решения уравнений
Приложение 3) показ слайдов демонстрационной презентации с решениями уравнений:
слайд №1- решение уравнения
слайд № 2- найдите абсциссы всех точек пересечения графиков функций 
слайд № 3- решение уравнения |log2х — 1| = (4 — 8x) (log2x — 1).
б) самостоятельная работа учащихся (каждый из учащихся может сам проверить свой уровень подготовки к ЕГЭ по данной теме. Ученикам предлагается тест, содержащий задания трех уровней сложности).
1. Решите уравнение log3(x+2)=3
2. Укажите промежуток, которому принадлежит корень уравнения log12(x+3)= log12(6-5x)
3. Найдите сумму корней уравнения 

5. Найдите произведение корней уравнения
1.Решите уравнение log11(2x+1)=2
2. Укажите промежуток, которому принадлежит корень уравнения –log5(4-х)= log152-1
3. Найдите сумму корней уравнения
2) 
3) 
4)
4. Напишите целые корни уравнения
Решите уравнение 3
1. Решите уравнение log0,5(2x-0,75)=2
2. Укажите промежуток, которому принадлежит корень уравнения
1) (-4;2); 2) (-2, 0); 3) (0;0,5); 4) (0,5;4)
3. Решите уравнение log3х+14
4. Найдите наибольший корень уравнения log3¦х+2¦+9= log3(х+2) 4
5. Решите уравнение
задания 1 2 3 4 5 Вариант 1 3 1 2 16 1 Вариант 2 3 1 2 49 -2 Вариант 3 4 2 81 25 -1
Проверка выполнения тестов на оценку. Анализ выполнения тестов.
VI. Подведение итогов урока
Учитель еще раз обращает внимание на те типы уравнений и теоретические факты, которые вспоминали на уроке, рекомендует выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет отметки. Каждый из учащихся проверил свой уровень подготовки к ЕГЭ по теме “Логарифмические уравнения” и делает для себя соответствующие выводы.
Решите уравнение (1—6).
1. 

3. log2 (x 2 + 10х + 25) = 2.
4.
Тесты по алгебре 10. тема «логарифмы»
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

В материале приведено несколько тестов в нескольких вариантах по теме «Логарифмы», логарифмическая функция. .
Просмотр содержимого документа
«Тесты по алгебре 10. тема «логарифмы»»
Тест №1 по теме «Логарифмы» I вариант
А1. Упростите выражение: 2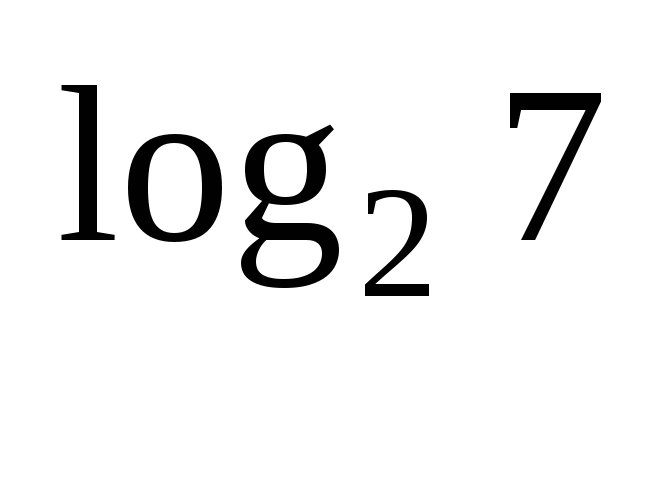
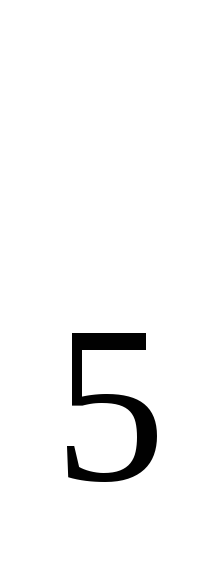
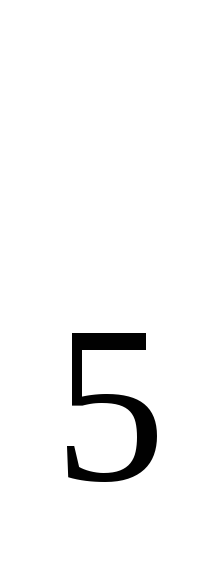
1) 9; 2) 32; 3) 51; 4) 4.
А2. Найди область определения функции у= log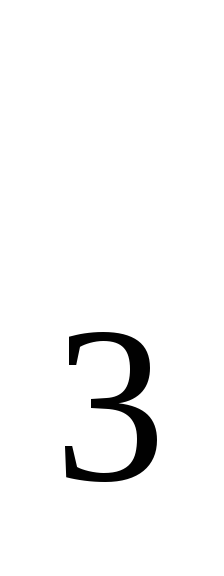
A3.Найдите множество значений функции у= 0,5 + log 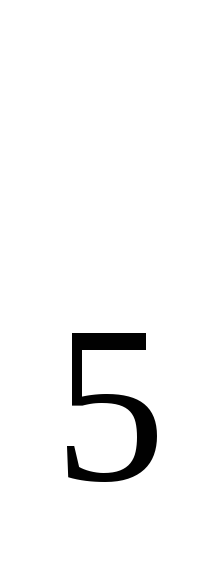
А4.Укажите промежуток, которому принадлежит корень уравнения
log 
1)(8,10); 2) (14,16); 3) (6,8); 4) (4; 6).
А5. Укажите, какому промежутку принадлежит корень уравнения:
log 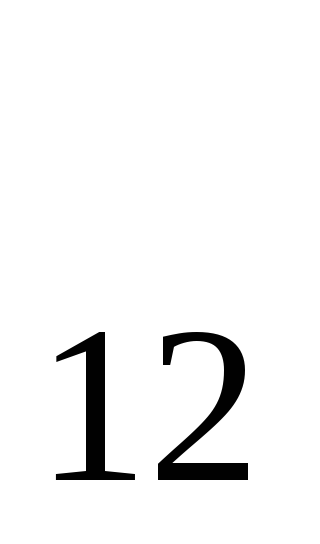
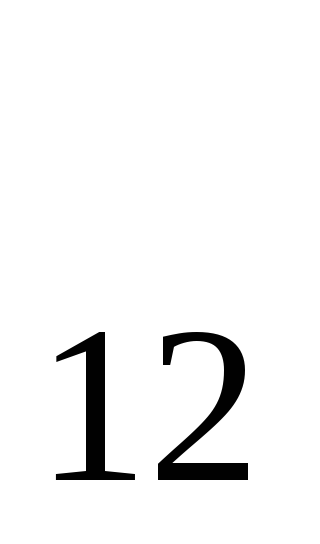
B1. Найдите наибольший корень уравнения.
log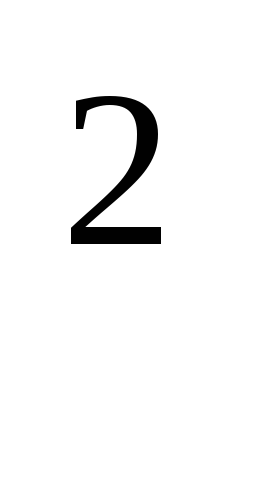

В2. Реши уравнение: 3∙10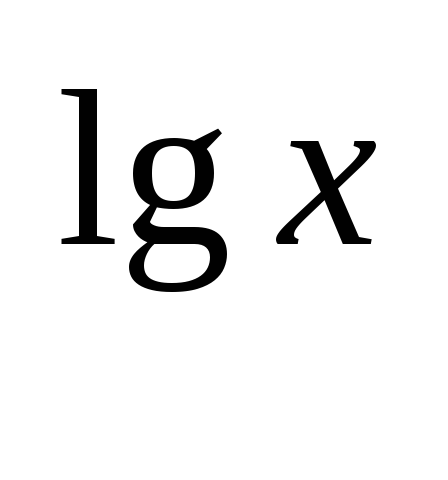
Тест №1 по теме «Логарифмы» II вариант
А1. Упростите выражение: 2
1) 24; 2) 8; 3) 12; 4) 7.
А2. Найди область определения функции у= log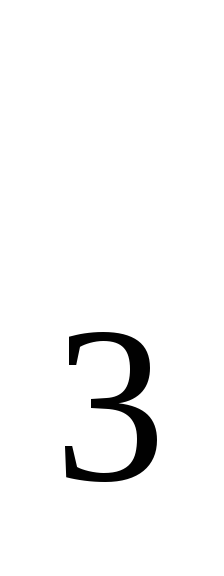
A3.Найдите множество значений функции у= 2 + log 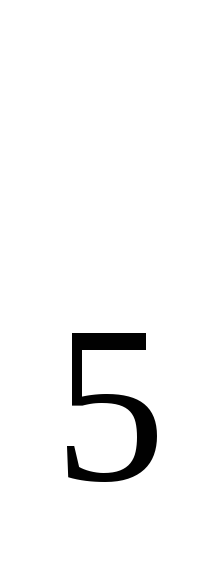
А4.Укажите промежуток, которому принадлежит корень уравнения
1) (19,21); 2) (–1,1); 3) (–11, –9); 4) (9; 11).
A5. Укажите, какому промежутку принадлежит корень уравнения:
log 

B1. Найдите наибольший корень уравнения.
log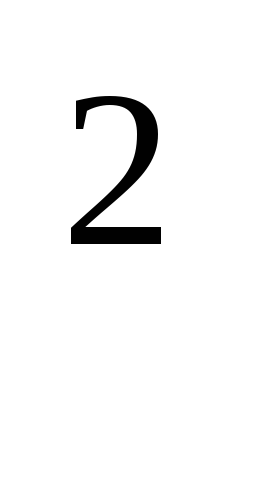

В2. Решите уравнение:
2∙25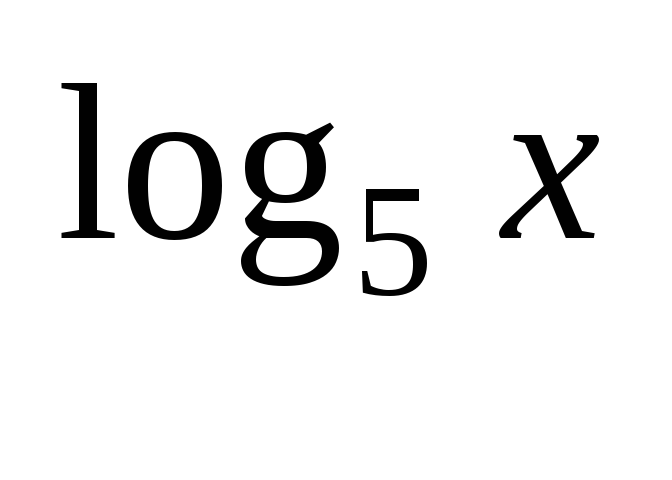
Тест №1 по теме «Логарифмы» I вариант
А1. Упростите выражение: 2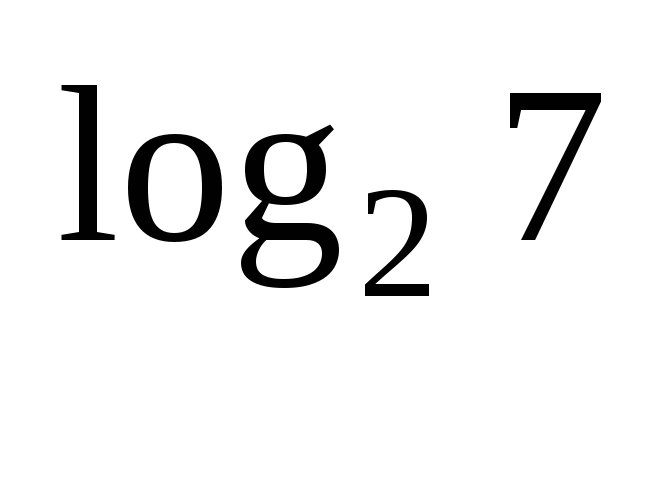
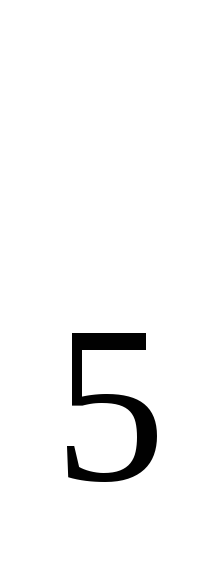
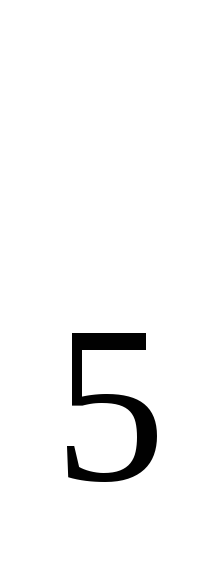
1) 9; 2) 32; 3) 51; 4) 4.
А2. Найди область определения функции у= log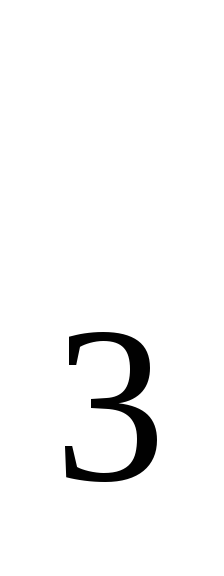
A3.Найдите множество значений функции у= 0,5 + log 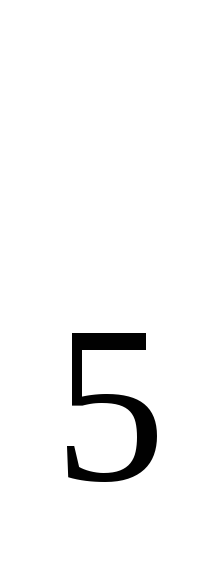
А4.Укажите промежуток, которому принадлежит корень уравнения
log 
1)(8,10); 2) (14,16); 3) (6,8); 4) (4; 6).
А5. Укажите, какому промежутку принадлежит корень уравнения:
log 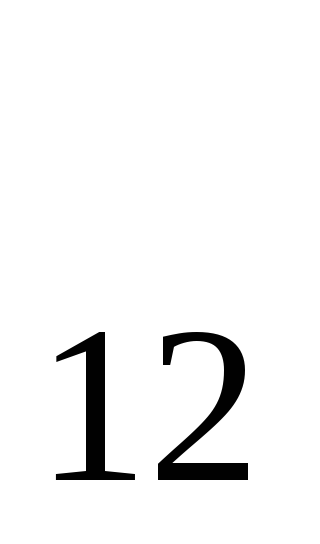
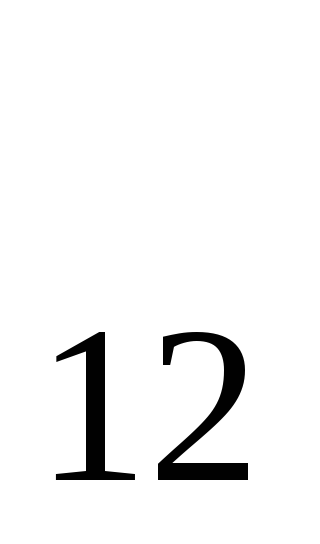
B1. Найдите наибольший корень уравнения.
log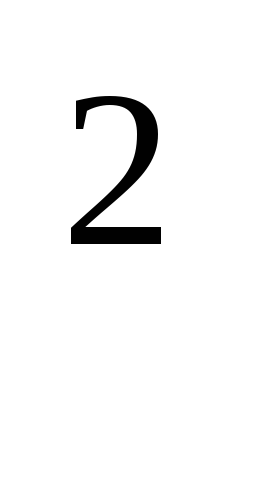

В2. Реши уравнение: 3∙10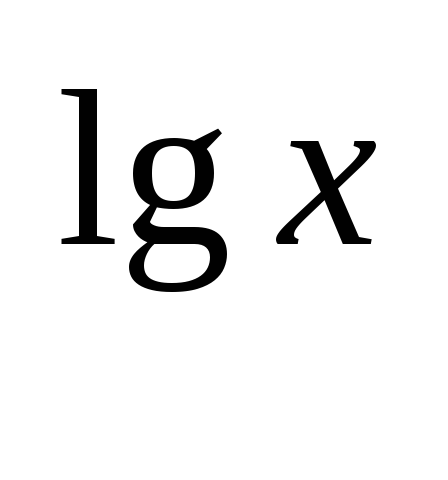
Тест №1 по теме «Логарифмы» II вариант
А1. Упростите выражение: 2
1) 24; 2) 8; 3) 12; 4) 7.
А2. Найди область определения функции у= log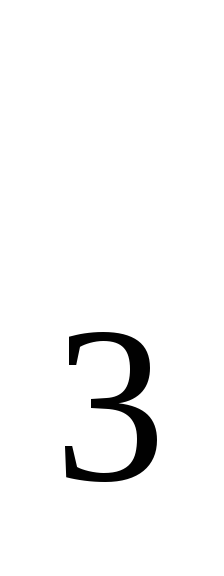
A3.Найдите множество значений функции у= 2 + log 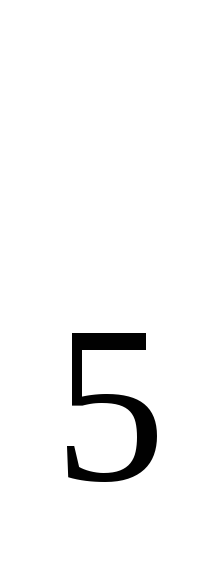
А4.Укажите промежуток, которому принадлежит корень уравнения
Видео:Отбор корней по окружностиСкачать

1) (19,21); 2) (–1,1); 3) (–11, –9); 4) (9; 11).
A5. Укажите, какому промежутку принадлежит корень уравнения:
log 

B1. Найдите наибольший корень уравнения.
log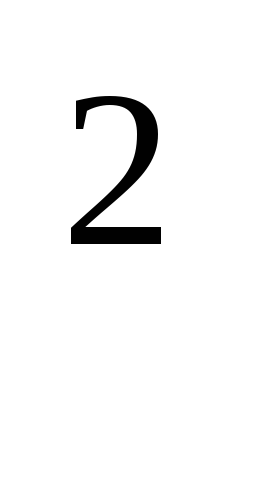

В2. Решите уравнение:
2∙25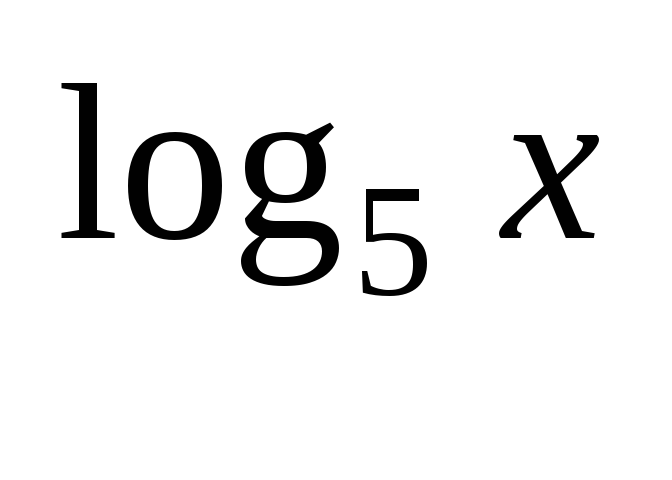
Т Е С Т №2 по теме «Логарифмы», 1 вариант
1. Укажите множество значений функции у = 12 х +4
2. Функция у = log 4 (x – 6) является
1) возрастающей, 2) убывающей, 3)не знаю.
3. Функция у = log 0,9 x принимает отрицательные значения
1) на интервале (1; +∞), 2) на интервале (0;1), 3) не знаю.
4.Задана функция у = 7 х . Найдите у(3)
5.Вычислите 81 3/4
6. Сравните: log 0,8 5 и log 0,8 12
Т Е С Т №2 по теме «Логарифмы», 2 вариант
1. Укажите множество значений функции у = 12 х – 5
2. Функция у = log 0,8 (x+4) является
1) возрастающей, 2) убывающей, 3)не знаю.
3. Функция у = log 5 x принимает положительные значения
1) на интервале (1; +∞), 2) на интервале (0;1), 3) не знаю.
4.Задана функция у = 6 х . Найдите у(3)
5.Вычислите 64 2/3
6. Сравните: log 6 0,1 и log 6 0,9
Т Е С Т №2 по теме «Логарифмы», 1 вариант
1. Укажите множество значений функции у = 12 х +4
Видео:Нахождение корней уравнения, принадлежащих промежуткуСкачать

2. Функция у = log 4 (x – 6) является
1) возрастающей, 2) убывающей, 3)не знаю.
3. Функция у = log 0,9 x принимает отрицательные значения
1) на интервале (1; +∞), 2) на интервале (0;1), 3) не знаю.
4.Задана функция у = 7 х . Найдите у(3)
1) 49, 2) 21, 3) 343.
5.Вычислите 81 3/4
6. Сравните: log 0,8 5 и log 0,8 12
Т Е С Т №2 по теме «Логарифмы», 2 вариант
1. Укажите множество значений функции у = 12 х – 5
2. Функция у = log 0,8 (x+4) является
1) возрастающей, 2) убывающей, 3)не знаю.
3. Функция у = log 5 x принимает положительные значения
1) на интервале (1; +∞), 2) на интервале (0;1), 3) не знаю.
4.Задана функция у = 6 х . Найдите у(3)
5.Вычислите 64 2/3
6. Сравните: log 6 0,1 и log 6 0,9
Самостоятельная работа. Вариант 1.
Задание A1. Найдите значение выражения: .
Задание A2. Найдите значение выражения : .
Задание A3. Найдите значение выражения: .
Задание A4. Найдите значение выражения: log3(9a) , если log3a 3 = 12 .
Задание A5. Найдите значение выражения: 3 + log303 + log3010.
Задание B1. Найдите х, если .
Задание B2. Найдите х, если .
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Задание B3. Найдите значение выражения .
Самостоятельная работа. Вариант 2.
Задание A1. Найдите значение выражения: log618 – log63 + 5.
Задание A2. Найдите значение выражения: .
Задание A3. Найдите значение выражения: log2(8a),если log216a = 16.
Задание A4. Найдите значение выражения: .
Задание A5. Найдите значение выражения: log525 – log50,2 + 3.
Задание B1. Найдите х, если .
Задание B2. Найдите х, если .
Задание B3. Найдите х, если .
Самостоятельная работа. Вариант 3.
Задание A1. Найдите значение выражения: .
Задание A2. Найдите значение выражения: .
Задание A3. Найдите значение выражения: log26 — log1627 + 13 .
Задание A4. Найдите значение выражения: .
Задание A5. Найдите значение выражения: 2log723 + 3log722.
Задание B1. Найдите х, если .
Задание B2. Найдите значение выражения .
Задание B3. Найдите х, если .
Самостоятельная работа. Вариант 4.
Задание A1. Найдите значение выражения: log62 + log63 + log66.
Задание A2. Найдите значение выражения: .
Задание A3. Найдите значение выражения: .
Задание A4. Найдите значение выражения : .
Задание A5. Найдите значение выражения: , если .
Задание B1. Найдите х, если .
Видео:Решение логарифмических уравнений #shortsСкачать

Задание B2. Найдите х, если .
Задание B3. Найдите значение выражения
🎬 Видео
Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

🔴 Найдите корень уравнения (1/7)^(x-5)=49 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Я теряю корни ★ 99 ошиблись ★ Решите уравнение ★ x^x=(1/2)^(1/2)Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Найдите наименьший положительный корень уравнения sin pi x/3=-(корень из 3)/2 (проф. ЕГЭ задача №6)Скачать

Математика 5 класс. Уравнение. Корень уравненияСкачать

🔴 Найдите корень уравнения (x-8)^2=(x-2)^2 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

ОГЭ вариант-8 #8Скачать

🔴 Найдите корень уравнения 2(3-2x)-7=-3x+8 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать


 ;
; ;
; ;
;