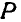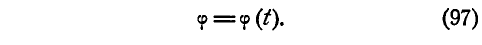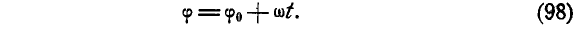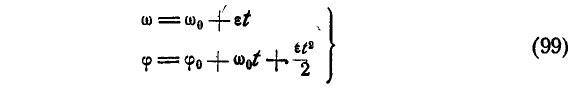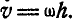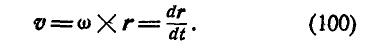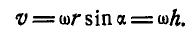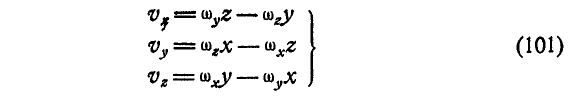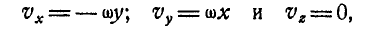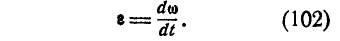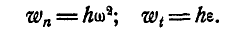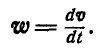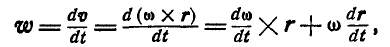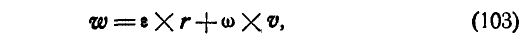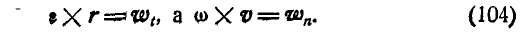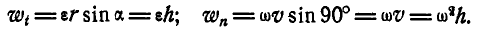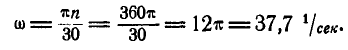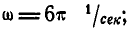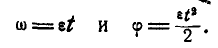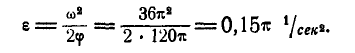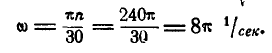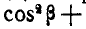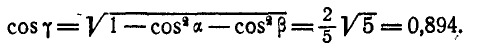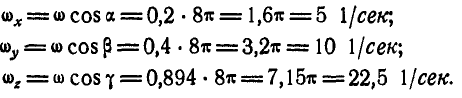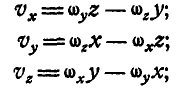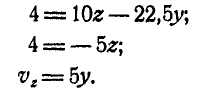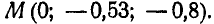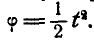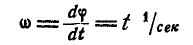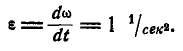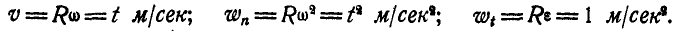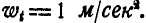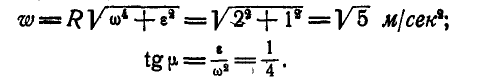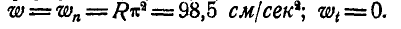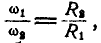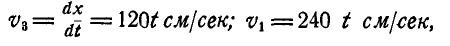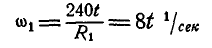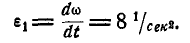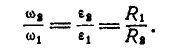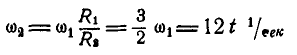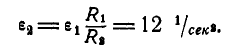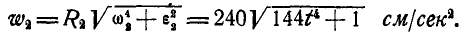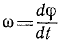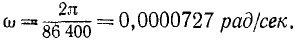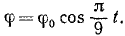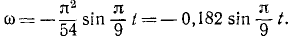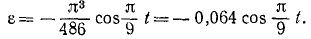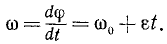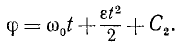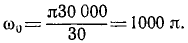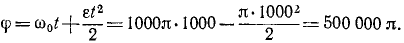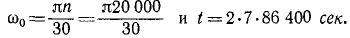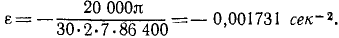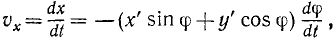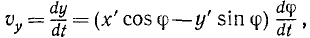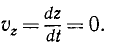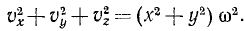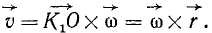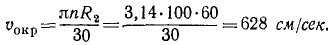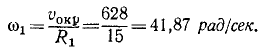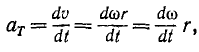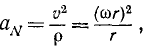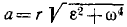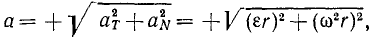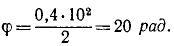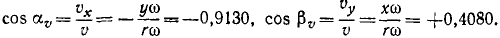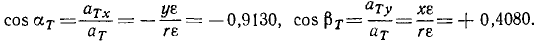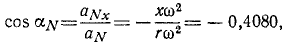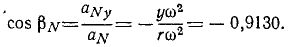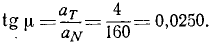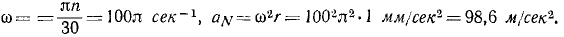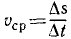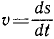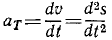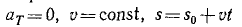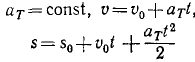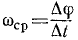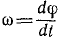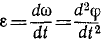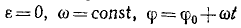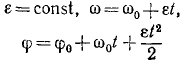- Теоретическая механика: Вращательное движение твердого тела
- § 33. Равномерное вращательное движение
- § 34. Равнопеременное вращательное движение
- § 35. Неравномерное вращательное движение
- Вращение твердого тела вокруг неподвижной оси в теоретической механике
- Вращение твердого тела вокруг неподвижной оси
- Вращательное движение
- Равномерное и равнопеременное вращения
- Траектории, скорости и ускорения точек вращающегося тела
- Траектории точек вращающегося тела
- Ускорение точек вращающегося тела
- Аналогия формул
- Кинематика вращательного движения твердого тела
- 📸 Видео
Теоретическая механика:
Вращательное движение твердого тела
Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.
Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.
Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.
Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.
Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими at и an.
Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).
Закон вращательного движения тела выражается уравнением
φ = f (t).
Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).
Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).
Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φоб.
Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.
Так как один полный оборот соответствует 2π рад, то
φ = 2πφоб и φоб = φ/(2π).
Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.
Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.
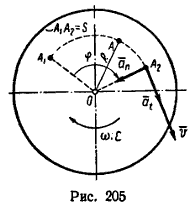
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, at и an, характеризующими движение различных точек этого тела (рис 205).
Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.
Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.
Касательное ускорение точки зависит от углового ускорения и определяется формулой
at = εR.
Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
an = ω 2 R.
При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

§ 33. Равномерное вращательное движение
Если угловая скорость ω=const, то вращательное движение называется равномерным.
Уравнение равномерного вращения имеет вид
φ = φ0 + ωt.
В частном случае, когда начальный угол поворота φ0=0,
φ = ωt.
Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.
Видео:Линейная и угловая скорости при равномерном движении по окружностиСкачать

§ 34. Равнопеременное вращательное движение
Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.
Уравнение равнопеременного вращения
(1) φ = φ0 + ω0t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω0 + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.
В эти формулы входят всего шесть величин: три постоянных для данной задачи φ0, ω0 и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.
Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.
Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ0 + (ω + ω0)t/2.
Исключим из (1) и (2) время t:
(4) φ = φ0 + (ω 2 — ω0 2 )/(2ε).
В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ0=0 и ω0=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).
Видео:Вращательное движение. 10 класс.Скачать

§ 35. Неравномерное вращательное движение
Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.
Видео:Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

Вращение твердого тела вокруг неподвижной оси в теоретической механике
Содержание:
Вращение твердого тела вокруг неподвижной оси:
Вращением тела вокруг неподвижной оси называется такое его движение, при котором две точки тела, например А и В, неподвижны (рис. 162). Прямая, проходящая через указанные две неподвижные точки, называется осью вращения. Если мысленно провести через тело две полуплоскости — неподвижную
При вращении тела угол поворота его 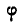
Уравнение (97) называется уравнением вращения; зная его, можно для любого момента t найти угол 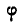
Величины угловой скорости и углового ускорения тела, вращающегося вокруг неподвижной оси, определяются по формулам (87) и (90).
Если 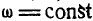
Поэтому такое уравнение по аналогии с равномерным движением точки называется уравнением равномерного вращения.
Точно так же, если 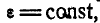
Уравнения равнопеременного вращения тела могут быть выведены аналогично уравнениям (82) и (83) равнопеременного движения точки путем замены линейных характеристик угловыми и записаны в виде:
Условимся угловую скорость вращающегося тела изображать вектором, отложенным по оси вращения в такую сторону, чтобы, смотря с конца этого вектора, вращение тела происходило в направлении, противоположном движению часовой стрелки (рис. 163).
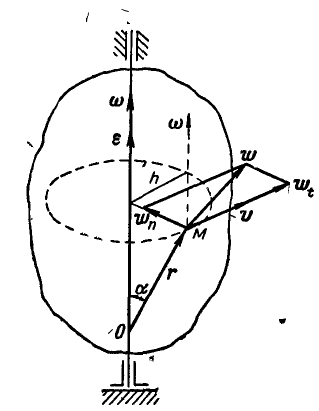
При вращении тела вокруг неподвижной оси (рис. 164) любая точка его М, отстоящая на расстоянии h от оси вращения, описывает окружность радиуса h и имеет линейную скорость, определяемую формулой (89):
Если провести из любой точки О оси радиус-вектор в точку М, то вектор линейной скорости точки М может быть представлен также в виде векторного произведения 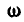
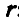
В самом деле, раскрывая векторное произведение, получим величину скорости, определяемую формулой (89):
Вектор же скорости направлен перпендикулярно к плоскости векторов 
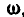
Рис. 164. Рис. 165.
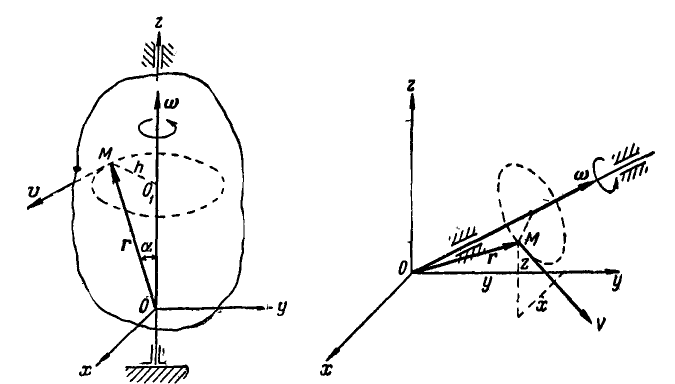
В самом общем случае, когда ось вращения тела составляет любые углы с координатными осями (рис. 165), проекции скорости точки М могут быть найдены по формулам проекций векторного произведения двух векторов (11):
Равенства (101) называются формулами Эйлера. Здесь 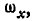
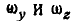
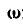
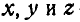
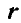
Если ось вращения вертикальна (рис. 164), то 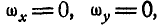
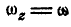
что было получено нами раньше (88). Мы уже знаем, что величина углового ускорения 
Введем в рассмотрение вектор углового ускорения е, под которым мы будем понимать векторную величину:
Так как 
При 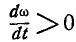
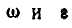
при 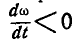
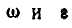
Нормальное и касательное ускорения любой точки М вращающегося тела (рис. 166) Moryт быть найдены по формулам (91):
Дадим векторное обобщение этим величинам. В самом общем случае вектор ускорения может быть найден по формуле (79):
Принимая во внимание формулы (100) и (102), имеем:
Действительно, в силу определения векторного произведения, находим:
Это приводит нас к формулам (91). Направления же 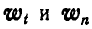
Задача №1
Маховик делает 360 об/мин. Найти его угловую скорость 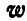
Решение. В нашем случае 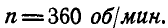
Задача №2
Маховик начинает вращаться равноускоренно из состояния покоя. Сделав с момента начала движения 60 оборотов, маховик имеет угловую скорость, равную 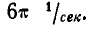
Решение. По условию задачи 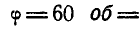
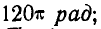
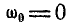
По формулам (99) получаем:
Подставляя значение 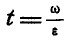
Задача №3
Тело делает 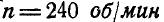
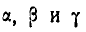
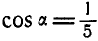
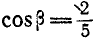
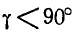
Найти такую точку тела, расположенную в плоскости 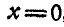
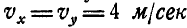
Решение. Угловая скорость:
Для определения 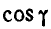
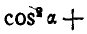
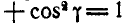
Найдем теперь проекции угловой скорости на координатные оси:
По формулам Эйлера (101) имеем:
Из первых двух уравнений находим, что 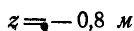
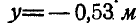
Задача №4
Маховик радиусом R = 1 м вращается вокруг неподвижной оси, проходящей через его центр перпендикулярно к плоскости чертежа, согласно уравнению
Найти скорость и ускорение точки М обода маховика по прошествии 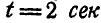
Решение. Найдем сначала по формулам (87) и (90) угловую скорость и угловое ускорение маховика:
Далее, линейная скорость, нормальное и касательное ускорения’ точки М в момент t найдутся по формулам (89) и (91):
При 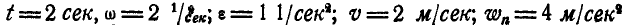
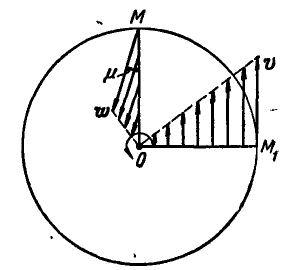
Величина и направление ускорения точки М определятся по формулам (92) и (93):
Так как величины линейных скоростей и ускорений точек, расположенных на одном из радиусов’маховика, например ОМ, зависят от величины самого радиуса, входящего в формулы (89) и (92) в первой степени, то отсюда следует, что концы векторов скоростей и ускорений точек одного радиуса будут расположены на прямой (рис. 167). Для удобства выполнения чертежа на радиусе ОМ дано изображение ускорений точек прямой ОМ, а на радиусе 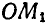
Задача №5
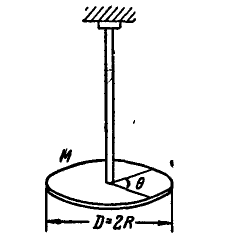
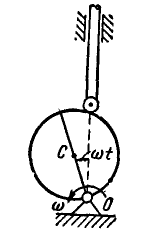
Диск, прикрепленный к вертикальной проволоке, совершает крутильные колебания вокруг оси проволоки так, что угол закручивания его меняется по закону: 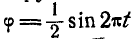
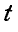
Найти нормальное, касательное и полное ускорения какой-либо точки М на ободе диска в момент 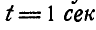
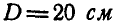
Указание: находим сначала угловую скорость и угловое ускорение диска по формулам (87) и (90), а затем ускорение точки М по формулам (91) и (92).
Ответ.
Рис. 169.
Задача №6
Зубчатое колесо А радиусом 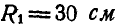
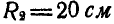
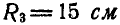
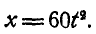
Решение. В общей точке касания колеса А и В имеют одинаковую линейную скорость, равную 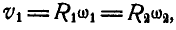
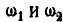
т. е. отношение угловых .скоростей колес обратно пропорционально их радиусам.
Найдем теперь угловую скорость 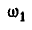
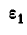
Вращение колес А и В равноускоренное, а поэтому 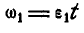
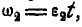
Отсюда угловая скорость 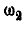
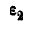
Ускорение какой-либо точки обода колеса В находим по формуле (92):
Видео:Ускорение при равномерном движении по окружностиСкачать

Вращение твердого тела вокруг неподвижной оси
Вращением вокруг неподвижной оси называют движение твердого тела, при котором его точки описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к их плоскостям
Вращательное движение
Как было показано, для определения движения твердого тела достаточно определить движение трех его точек, не лежащих на одной прямой. Пусть во- время движения тела две его точки О и O1 остаются неподвижными.
Тогда движение тела можно определить движением третьей точки К, принадлежащей телу и не лежащей на одной прямой с точками О и O1. Выберем эту точку произвольно и, соединив все три точки прямолинейными отрезками, получим треугольник OO1K-Так как точки О и O1 неподвижны, то неподвижна и сторона OO1 треугольника OO1K, и движение точки К, а также и всего тела определится поворотом плоскости треугольника OO1K вокруг прямой OO1. Точку К мы выбрали произвольно, следовательно, поворачивается вокруг прямой OO1 любая плоскость, проведенная в теле через эту прямую. Такое движение тела называют вращательным движением, или, коротко, вращением, а неподвижную прямую OO1, вокруг которой вращается тело, называют осью вращения.
Ось вращения может проходить и за пределами тела. Так, например, Луна, двигаясь вокруг Земли, повернута к ней всегда одной стороной. Движение Луны по отношению к Земле можно назвать вращением. Ось вращения проходит за пределами Луны через центры круговых траекторий ее точек.
Если движение тела определять по движению его точек, то вращение вокруг оси можно определить как движение твердого тела, при котором все точки тела описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к плоскостям этих окружностей, а ось вращения можно определить как неподвижную прямую, на которой расположены центры окружностей, описываемых точками вращающегося тела.
Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела: φ=φ(t)
Уравнение вращательного движения. Построим основную систему координат xcyz, направив ось Oz по оси вращения тела (рис. 101). Эта система неподвижная и не связана с вращающимся телом. Построим теперь другую, подвижную, систему координат x’0y’z’, направив ось Oz’ также по оси OO1 вращения тела, а ось Ox’ — на какую-либо точку K1 тела. Эта система координат неизменно связана с телом и поворачивается вместе с ним относительно основной системы xOyz. Угол φ на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела, называют углом поворота и обозначают буквой φ. Так, если в начальное мгновение оси Ox’ и Ox (см. рис. 101) совпадали, то углом поворота мы назовем двугранный угол между неподвижной плоскостью xθz и подвижной плоскостью x’Oz’ или равный ему линейный угол x’Ox’.
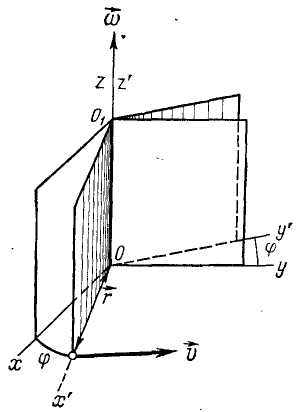
Рис. 101
Угол φ можно рассматривать как угловую координату тела, потому что он определяет положение всего вращающегося тела. Измеряется угол φ в радианах.
Будем считать угол φ положительным, если он отсчитан от положительной оси Ox к положительной оси Оу, т. е. против вращения часовой стрелки, если смотреть с положительного направления оси Oz. При отсчете в противоположную сторону будем считать угол отрицательном.
Чтобы определить вращение тела, надо знать угол поворота как некоторую непрерывную однозначную функцию времени:
Уравнение (82) является уравнением вращательного движения твердого тела вокруг неподвижной оси.
Всякая плоскость OO1K, проведенная через ось вращения и какую-либо точку К тела, поворачивается за данное время на такой же угол φ, на который за это же время повернулась плоскость x’Oz’. Это следует из условия неизменяемости твердого тела.
Угловая скорость выражается первой производной от угла поворота по времени:
Угловая скорость. Угол поворота характеризует вращение тела только с геометрической стороны. Чтобы охарактеризовать вращение тела не только в пространстве, но и во времени, возьмем отношение изменения ∆φ угла поворота ко времени Δt, в течение которого это изменение происходило, называемое средней угловой скоростью тела:
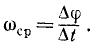
Пределом отношения (83′) при Δt, стремящимся к нулю, является первая производная от угла поворота по времени. Она характеризует изменение угла поворота в данное мгновение, т. е. характеризует вращение тела не только по отношению к окружающему пространству, но и во времени. Эта величина принята за пространственно-временную меру вращения твердого тела вокруг оси и ее называют угловой скоростью тела:
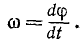
Знак производной (83) указывает, в какую сторону поворачивается тело вокруг оси Oz: если производная (83) положительна, то наблюдатель, смотрящий с положительной стороны оси Oz, видит тело вращающимся против часовой стрелки, т. е. справа налево — от положительного направления оси Ox к положительному направлению оси Оу: при отрицательной производной (83) вращение тела происходит в обратном направлении.
Размерность угловой скорости равна размерности угла поворота, деленной на размерность времени. Но угол поворота является отвлеченной величиной, и размерность его—единица. Следовательно, размерность угловой скорости обратна размерности времени.
Чаще всего время измеряют в секундах, тогда единица угловой скорости ceκ -1 .
Равномерное вращение иногда характеризуют числом п оборотов, совершаемых телом за единицу времени (обычно за минуту).
Найдем соотношение между угловой скоростью ω, выраженной в радианах в секунду, и числом оборотов в минуту. Если тело делает n оборотов в минуту, то оно поворачивается за каждую минуту на 2πn радианов, а за секунду—в 60 раз меньше, следовательно,
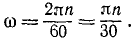
Формулу (84) широко применяют в технической механике. Приближенно можно считать
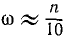
В формулах (84) и (84′) n выражеyо в оборотах за минуту, a ω — в радианах за секунду, как их большей частью и выражают. Однако для очень медленно вращающихся тел число оборотов удобнее считать не за минуту, а за другие единицы времени. Так, Земля вращается вокруг своей оси, делая 1 оборот в сутки. Было бы неудобно считать, что Земля делает 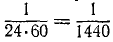
Самые медленные вращения встречаются в звездном мире. Так -2 .
Чаще всего время измеряется в секундах, тогда единица углового ускорения ceκ -2 , или по записи, рекомендованной ГОСТом, pa∂/ceκ 2 .
Если с течением времени абсолютная величина угловой скорости тела увеличивается, то производная 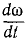
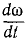
Задача №7
Унифиляр (тело, подвешенное на вертикальном стержне) (рис. 102) закрутили на угол 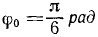
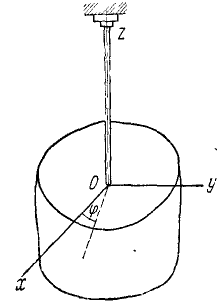
Рис. 102
Определить угловую скорость (в ρa∂/ceκ.) и угловое ускорение (в рад/сек) через каждые 3 сек от начала движения.
Решение. Дифференцируя уравнение движения, получим выражение угловой скорости унифиляра:
Дифференцируя вторично найдем, угловое ускорение унифиляра:
Чтобы определить угол поворота, угловую скорость и угловое ускорение в заданные мгновения, надо в уравнение движения тела и в полученные соотношения подставить t = 3, 6, 9, . и т. д. секунд. Анализируя полученные данные относительно ω и ε, убедимся, что унифиляр совершает крутильные колебания с периодом 18 сек.
Равномерное и равнопеременное вращения
Если угловая скорость ω постоянна, то производная 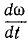
ε = 0, ω = const, φ = φ0+ωt, (86)
где φ0-начальное значение угла.
Формулы (86) справедливы только для равномерного вращения тела и неприменимы при других движениях.
Из различных переменных вращений тела в задачах наиболее часто встречается равнопеременное вращение. Равнопеременным вращением называют такое вращение твердого тела вокруг оси, πph котором угловое ускорение остается постоянным:
Интегрируя это уравнение, находим
Постоянную интегрирования C1 находим из начальных данных. В начальное мгновение (при t=0) величина угловой скорости была ω0. Подставляя эти частные значения аргумента t и функции ω, находим постоянную C1:
Интегрируя это равенство, получаем
Постоянную C2 находим из начальных данных. Если при начале вращения тело было повернуто на некоторый угол φ0, то, подставляя φ0 вместо φ и 0 вместо t, найдем C2 = φ0. Для равнопеременного вращения тела имеем:
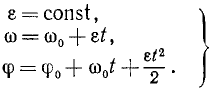
Формулы (87) справедливы только для равнопеременного вращения твердого тела и неприменимы при других движениях.
Задача №8
Барабан суперцентрифуги делает при установившемся движении 30000 об/мин, а после прекращения подачи энергии (на выбеге) вращается равнозамедленно с угловым ускорением ε=π1∕ceκ 2 . Определить время выбега (время до остановки) и угол поворота барабана за это время.
Решение. В мгновение прекращения подачи энергии угловая скорость барабана была
C этого мгновения барабан вращается равнозамедленно по (87):
В мгновение остановки барабана угловая скорость его равна нулю. Подставляя это значение угловой скорости, находим время выбега.
t = 1000 сек = 16 мин 40 сек.
За это время барабан повернется на угол
Чтобы по углу поворота определить число оборотов, надо поделить этот угол (выраженный в радианах) yа 2π—число радианов в одном обороте.
Ответ. t = 16 мин 40 сек, φ = 250 000 об.
Задача №9
В инерционном аккумуляторе Уфимцева (1918 г.) для ветроэлектрических станций стальной диск вращается в глубоком вакууме, делая 20 000 об/мин. Предоставленный самому себе, он продолжает вращаться в течение двух недель. Определить е диска, считая вращение равнозамедленным.
Решение. Определим начальную угловую скорость диска н время (2 нед.) до остановки в секундах:
Ответ получим, разделив ω0 на t.
Ответ.
Траектории, скорости и ускорения точек вращающегося тела
Точки вращающегося тела, расположенные на одной прямой, параллельной оси вращения, совершают одинаковые движения
Траектории точек вращающегося тела
Вращением тела называют движение, при котором точки тела описывают окружности с центром на оси вращения. Следовательно, по самому определению вращательного движения траектории точек тела—окружности.
Если тело мысленно пересечь какой-либо плоскостью, перпендикулярной оси вращения, то в этой плоскости будут находиться круговые траектории всех расположенных в ней точек тела. Очевидно, что движения точек тела, лежащих на ном в какой-либо из точек к этой плоскости, совершенно одинаковы, а потому и движение точек всего тела может быть полностью охарактеризовано движением точек, лежащих в этой плоскости.
Сохраним и в этом параграфе расположение осей координат (см. рис. 101), при котором оси Oz и Oz’ неподвижной и подвижной систем совпадают с осью вращения тела, а плоскость x’0y’ находится в плоскости хОу.
Возьмем в этом теле какую-либо точку К (рис. 103), координаты которой относительно подвижной системы обозначимx’,y’ и г’. Эти координаты точки К во время вращения тела не меняются, так как оси подвижной системы координат неизменно связаны с телом и вращаются вместе с ним. Координаты той же точки в основной системе обозначим х, у и z.
Координаты х и у точки К связаны с координатами х’ и у’ той же точки формулами, известными из аналитической геометрии и понятными из чертежа (рис. 103):
х = х’ cos φ—y’ sin φ, (88′)
y = x’ sin φ +y’ os φ. (88″)
Если тело вращается, то с течением времени меняется угол φ, являющийся некоторой функцией (71) от времени t, а следовательно, меняются и координаты х и у точки К в основной системе отсчета. Координата же z при направлении оси Oz вдоль оси вращения не изменяется и остается равной z’:
Аналогично можно определить подвижные координаты по неподвижным и углу φ:
х’ = х cos φ у sin φ; y’ = y cos φ—x sinφ; z’ = z.
Скорость точки тела, вращающегося вокруг оси, равна произведению угловой скорости тела на расстояние точки от оси: υ= ωr
Скорости точек вращающегося тела. Для получения проекций скорости на неподвижные оси координат продифференцируем по времени равенства (88), рассматривая φ как функцию времени. Будем иметь
Но согласно (88) выражение, стоящее в скобках в первом из этих равенств, есть у, а во втором х, а потому 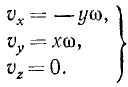
Возводя эти равенства в квадрат и складывая, найдем
Но в левой части мы имеем квадрат полной скорости точки, а в скобках правой части — квадрат расстояния точки от оси. Мы получили одну из главнейших формул кинематики:
υ = ωr (90)
— величина скорости точки вращающегося тела равна произведению угловой скорости тела на расстояние точки от оси вращения.
Таким образом, для определения скорости точки вращающегося тела нет необходимости знать ее координаты, надо знать лишь расстояние точки от оси вращения и угловую скорость тела.
Можно определить угловую скорость тела по скорости какой-либо из его точек и по расстоянию этой точки от оси вращения:
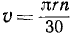
По этим формулам можно определить скорость любой точки вращающегося тела, независимо от того, какую форму имеет тело и находится точка на поверхности или внутри тела. Скорость точки тела, вращающегося вокруг оси, называют вращательной скоростью точки. Она направлена перпендикулярно к плоскости, проходящей через точку и ось вращения, против хода часовой стрелки или по ходу часовой стрелки в зависимости от знака производной (83).
Если же смотреть на тело с той стороны оси вращения, куда мы направили вектор 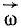
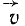
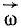
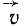
Следовательно, вектор вращательной скорости точки и по величине и по направлению можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Его можно представить в виде векторного произведения аналогично тому, как это сделано в статике с моментом силы относительно точки.
Вращательную скорость точек, лежащих на поверхности цилиндра (шкива, барабана, махового колеса, вала и т. п.), вращающегося вокруг своей оси, называют окружной скоростью тела. Окружная скорость равна произведению ω на радиус R тела:
Задача №10
Определить вращательную скорость точек земной поверхности на экваторе и на широте Москвы (55°45′) при вращении Земли вокруг оси (рис. 104). Средний радиус Земли 6371 км и cos 55 o 45′ = 0,5628.
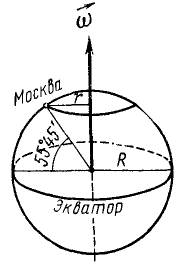
Рис. 104
Решение. Вращаясь вокруг своей оси, Земля совершает один оборот (2π рад) за сутки (86 400 сек), и угловая скорость Земли ω=727∙10 -7 pa∂/ceκ. Умножая угловую скорость на радиус Земли, выраженный в метрах (6371 ∙ 10 3 ), найдем вращательную скорость точек Земли на экваторе:
υ= ωR=727 • 6371 • 10 -4 = 463 м/сек.
Для определения вращательной скорости точек в Москве надо умножить ω Земли на расстояние г от Москвы до земной оси:
υ = 727 • 10 -7 • 0,5628 • 6371 • 10 3 = 261 м/сек.
Ответ. Вращательная скорость точек на экваторе 463 м/сек, в Москве 261 м/сек.
Она направлена против вращения часовой стрелки, если смотреть с северного полюса.
Задача №11
Шкив динамомашины R1= 15 см (рис. 105) вращается посредством бесконечного ремня от паровой машины со шкивом R2 — 60 см, делающим 100 об/мин. Определить угловую скорость ω1 шкива динамомашины.
Рис. 105
Решение. Определим окружную скорость шкива паровой машины:
Такова же величина скорости частиц ремня, а следовательно, и окружная скорость шкива динамомашины. Его угловая скорость
Ответ. ω1=41,87 рад/сек, n = 400 об/мин.
Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения тела: αr=er
Ускорение точек вращающегося тела
Если в выражении касательного (69) и нормального (74) ускорений вместо скорости v мы подставим выражение (90) вращательной скорости, то получим касательное и нормальное ускорения точки тела, вращающегося вокруг неподвижной оси.
Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения.
Центростремительное ускорение точки вращающегося тела равно произведению квадрата угловой скорости тела на расстояние точки от оси вращения тела:
αN=ω 2 r
Каждая точка вращающегося тела описывает окружность, а потому радиус кривизны р траектории точки равен расстоянию этой точки от оси вращения тела. Имеем
Нормальное ускорение точки вращающегося тела обычно называют центростремительным ускорением. Оно равно произведению квадрата угловой скорости на расстояние точки от оси вращения тела.
Величина полного ускорения точки тела, вращающегося вокруг оси, выражается формулой
Зная касательное и центростремительное ускорения, определим по формуле (75) величину полного ускорения этой точки:
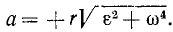
Иногда бывает необходимо определить проекции ускорения точки вращающегося тела на неподвижные оси координат. Для этого продифференцируем равенства (89) по времени, учитывая, что при вращении тела меняется не только его угловая скорость, но и координаты х и у его точек:
Подставляя вместо υx и υy их значения (89), найдем проекции ускорения точки вращающегося тела на неподвижные оси:
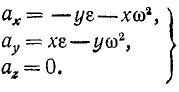
Возводя в квадрат и складывая, найдем
a 2 = (x 2 + y 2 ) (ε 2 + ω 4 ),
или, так как x 2 +y 2 = r 2 , получаем уже знакомую нам формулу (94). Следовательно,
Задача №12
Тело вращается вокруг оси Oz без начальной угловой скорости и с постоянным угловым ускорением ε = 0,4 рад/сек 2 . Определить для t = 10 сек: 1) координаты точки К тела, если при t = 0 координаты точки К были: х = +10, y=0, z-0∙, 2) ее вращательную скорость; 3) направляющие косинусы вращательной скорости; 4) касательное и центростремительное ускорения той же точки; 5) направляющие косинусы касательного и центростремительного ускорений; 6) угол, составляемый векторами полного и центростремительного ускорений.
Решение. Тело вращается равноускоренно; по (87) найдем угловое ускорение, угловую скорость и угол поборота тела для заданного мгновения: ε = 0,4 ρaд/ceκ 2 ; ω = 0,4 • 10 = 4 ρaд/ceκ;
Тело повернулось за 10 сек на 20 рад. Переведем радианы в градусы:
за вычетом полных оборотов определим угол αr, составляемый радиусом-вектором с осью Ox (рис. 106):
20 рад = 65 о 54’56»,
По тригонометрическим таблицам находим: cos ar = 0,4080, sin ar = 0,9130. Приняв во внимание, что расстояние точки К от оси вращения тела равно 10 см, найдем координаты точки К в мгновение t=10 сек:
х=10 cos ar = +4,080 см,
y = 10 sin ar = +9,130 см.
Величину вращательной скорости определим по (90):
υ = ωr = 4 • 10 = 40 см/ceκ.
Чтобы определить направляющие косинусы вращательной скорости, найдем сначала по (89) ее проекции на оси координат:
υx= — yω = — 36,52 см/сек,
по затем по (62) — направляющие косинусы:
Определим по (92) величину касательного ускорения:
и по (95′) — проекции касательного ускорения на оси х и у:
aTx = — yε=—3,652 см/сек 2 , aTy = xε =+1,632 см/сек 2 .
Разделив проекции на модуль касательного ускорения, найдем направляющие косинусы касательного ускорения:
Мы видим, что направляющие косинусы касательного ускорения тождественны с направляющими косинусами скорости.
Напомним, что знак направляющего косинуса определяется знаком числителя. Если ω и ε имеют одинаковые знаки (как в данной задаче), то тело вращается ускоренно и направление касательных ускорений его точек совпадает с направлением их скоростей, если же знаки ω и ε различны, то вращение замедленное и векторы касательных ускорений и скоростей точек направлены в противоположные стороны.
Величину центростремительного ускорения определим по (93);
aN=ω 2 r = 4 2 ∙10 = 160 см/сек 2
и по (95′) —его проекции на оси координат:
aNx=—xω 2 = —65,280 см/сек 2 ,
aNy = — yω 2 = —146,080 см/сек 2 .
Проекции нормального ускорения точки на оси координат имеют знаки, обратные знаку соответствующей координаты точки. В самом деле, ayx отрицательна, если абсцисса х положительна, и положительна, если х отрицательна (аналогично и ayy). Следовательно, центростремительное ускорение всегда направлено к началу координат, т. е. к центру круговой траектории точки.
Разделив проекции центростремительного ускорения на его модуль, найдем направляющие косинусы центростремительного ускорения:
Так как касательное ускорение перпендикулярно к центростремительному, то (по условию перпендикулярности, известному из аналитической геометрии) сумма произведений соответствующих направляющих косинусов должна равняться нулю. Действительно,
cos aT cos aN + cos βT cos βN = ( — 0,9130) ( —0,4080) + ( + 0,4080) ( — 0,9130) =0.
Определим теперь тангенс угла между направлением полного и нормального ускорений:
Пользуясь таблицами тригонометрических функций, определим, что угол равен l o 26’0″.
Ответ. 1) х = + 4,080 см, у = + 9,130 см; 2) υ = 40 см/сек, 3)cos aυ=—0,9130, cos βυ = +0.4080; 4) aT = 4 см/сек1, aN= 160 см/сек 2 ; 5) cos aT=—0,9130, cos βT= +0,4080, cos aN = — 0,4080, cos βN=—0,9130; 6) угол равен l o 26’0″.
Задача №13
При сборке ротора молотковой дробилки была допущена неточность, в результате которой центр тяжести ротора отстоит от оси вращения на расстоянии 1 мм. Определить центростремительное ускорение центра тяжести ротора, если n = 3000 об/мин.
Решение. По формулам (84) и (93) имеем
Ответ. aN=98,6 м/сек 2 ≈ 10g.
Зависимости между углом поворота, угловой скоростью, угловым ускорением и временем аналогичны зависимостям между расстоянием, скоростью, касательным ускорением и временем
Аналогия формул
Формулы кинематики вращательного движения аналогичны соответствующим формулам кинематики точки и могут быть из них получены, если заменить расстояние s углом поворота φ, скорость υ— угловой скоростью ω и касательное ускорение αT-угловым ускорением ε. Это правило является мнемоническим, оно непригодно для вывода формул, но может облегчить их запоминание. Ниже приведен ряд формул, получающихся одна из другой такой заменой.
| Движение точки | Вращение точки | |||
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Сферическое движение твердого тела
- Плоско-параллельное движение твердого тела
- Движение твердого тела, имеющего неподвижную точку
- Движение твердого тела
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Лекция 6.4 | Линейная скорость и ускорение при равномерном вращении | Александр Чирцов | ЛекториумСкачать

Кинематика вращательного движения твердого тела
Вращательное движение очень распространенно в природе и технике. Недаром, вторая техническая революция цивилизованного общества началась с изобретения человеком колеса. Без знания основных законов вращательного движения совершенно невозможно понять ни закономерностей движения планет и космических аппаратов, ни законов микромира.
Законы вращательного движения — это не новые законы механики, а лишь результат приспособления законов ньютоновской механики к данной задаче, оформления их математически в удобной для рассмотрения и решения той или иной задачи, связанной с вращательным движением.
Для описания вращательного движения нельзя пользоваться такой моделью как материальная точка, здесь уместно говорить о системе материальных точек, из которых состоит твердое тело. Целесообразно использовать абстрактную модель абсолютно твердого тела.
Абсолютно твердым телом называют такое тело, расстояние между двумя соседними точками которого в процессе вращения остается неизменным.
Наиболее простой случай вращательного движения абсолютно твердого тела — это вращение его относительно закрепленной (неподвижной) оси.

 |

При вращательном движении абсолютно твердого тела все точки двигаются по окружностям, центры которых лежат на прямой ОО’, называемой осью вращения.


Следовательно, для всех точек твердого тела можно ввести однозначные характеристики за данный промежуток времени: угловой путь, угловую скорость, угловое ускорение.
В качестве кинематических характеристик вращательного движения твердого тела выбраны: вектор углового перемещения φ, угловая скорость ω, угловое ускорение ε.
При малых углах поворота |dφ|=dφ и направлен вдоль оси вращения ОО’ против часовой стрелки (правило правого винта).
Векторы, направления которых связываются с направлением вращения, называются аксиальными векторами , которые не имеют определенных точек приложения: они могут откладываться от любой точки оси вращения.
При вращательном движении с течением времени угловой путь изменяется. Быстроту изменения углового пути со временем характеризуют векторная величина 



Взяв отношение изменения длин дуг окружностей 
Таким образом, угловой путь 






V=R*ω, или в векторной форме можно записать как 
Таким образом, быстроту изменения углового пути со временем характеризует векторная физическая величина 
В системе СИ угловой путь (угол поворота) измеряют в радианах – это центральный угол, опирающийся на дугу, длина которой равна радиусу. 
При равномерном движении по окружности угловая скорость является постоянной величиной ω=const. Кроме этих кинематических величин равномерное движение тела по окружности можно выразить через период и частоту вращения.
Время, в течении которого тело (точка) совершает один оборот, называется периодом вращения. 
Число полных оборотов N связано с угловым путем соотношением 
Число оборотов тела (точки) вокруг центра вращения за единицу времени называют частотой вращения.
Исходя из определений периода и частоты можно записать следующее соотношения: 

В системе СИ период выражают секундах [T]=[1c]=[c], то частота [

Кроме равномерного вращательного движения твердого тела рассматривают случай, когда ω≠const и изменяется со временем. Быстроту изменения угловой скорости со временем характеризует физическая величина – угловое ускорение.
Пусть за время ∆t линейная и угловая скорости точки твердого тела получили приращение на величину ∆V, 
Поделим левую часть и правую часть уравнения на ∆t, за которое произошло изменение скоростей
Величина 

Для получения мгновенных значений соответствующих величин необходимо использовать формулу (26) и взять предел этих отношений, устремив
Таким образом, угловое ускорение есть первая производная от угловой скорости по времени 

При ускоренном движении вектор 



Вектор 
тогда модуль полного ускорения
1.5 Основные формулы для решения задач.
1. Задание радиус – вектора в координатной форме:
2. Модуль радиус вектора:
3. Приращение радиус-вектора:
4. Средняя скорость:
5. Мгновенная скорость:
6. Задание вектора скорости в координатной форме:
7. Модуль скорости:
8. Вычисление скорости при прямолинейном движении
10. Мгновенное ускорение:
11. Задание вектора ускорения в координатной форме:
12. Модуль ускорения:
13. Средняя угловая скорость:
14. Мгновенная угловая скорость:
15. Среднее угловое ускорение:
16. Мгновенное угловое ускорение:
17. Связь линейной скорости с угловой:
18. Полное ускорение:
19. Модуль полного ускорения:
20. Связь между линейными кинематическими характеристиками с соответствующими угловыми:
1.6. Задачи для самостоятельного решения.
1. Вектор скорости 



2. Начальное значение радиус-вектора 

1) Приращение радиус вектора
2) Модуль приращения
3) Приращение модуля 
3. Радиус-вектор точки изменяется со временем по закону: 





4. Радиус-вектор точки изменяется со временем по закону: 
5. Точка движется со скоростью 
1) Модуль скорости 
2) Ускорение точки 

3)Пройденный путь S точкой с момента времени t1=1c до момента t2=4c.
6. Зависимость координат частиц от времени имеет вид: 

1) Радиус-вектор частицы 


2) Модуль радиус-вектора 


7. Кинематическое уравнение движения материальной точки оси Ox имеет вид: 
1) Координату x точки; 2) Мгновенную скорость V; 3) Мгновенное значение ускорения 
8. Уравнение прямолинейного движения по оси Ох имеет вид: 
9. Движение материальной точки задано уравнением: 
10. Точка движется по прямой и зависимость пройденного пути от времени задается уравнением: 
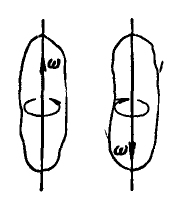
11. Тело участвует в двух вращениях, происходящих со скоростью 


12. Материальная точка движется по плоскости согласно уравнению 


13. Движение материальной точки задано уравнением: 






14. Точка движется по окружности радиусом R=10м согласно уравнению 
15. Диск радиусом R=10см вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением: 
16. Движение точки по кривой задано уравнением: 

17. Диск радиусом R=10см, находившийся в состоянии покоя начал вращаться с постоянным угловым ускорением 
18. Маховик начал вращаться равноускоренно и за промежуток времени 

19. Диск вращается с угловым ускорением 

20. Найти угловое ускорение колеса, если известно, что через 


1. Радиус-вектор 
б) направленный отрезок прямой, начало которого в начале координат, а конец упирается в движущуюся материальную точку;
в) направленный отрезок прямой заданный только числовым значением.
2. Каким способом можно разложить радиус-вектор 
а)
б)
в)
3. Если 

а)
б)
в)
4. Радиус-вектор 

а) 5; б) 25; в) 
5. Перемещение это:
а) вектор, соединяющий начальное положение мат. Точки с её конечным положением;
б) расстояние, пройденное точкой вдоль траектории её движения;
в) отрезок прямой, соединяющий начало траектории движения мат. точки с концом этой траектории.
6. В каком случае
а) криволинейного движения;
б) прямолинейного движения;
в) движения по окружности, эллипсу, гиперболе.
7. В координатной форме вектор скорости 
а)
б)
в)
8. Модуль вектора скорости 
а)
б)
в)
г)
9. Какое из движущихся равномерно, тел имеет большую скорость:
а) 1; б) 2; в) 3; г) 4.
10. Равномерным называют движение скорость которого:
а) остается постоянной с изменением времени;
б) изменяется одинаково за любые равные промежутки времени;
в) монотонно возрастает за любые промежутки времени;
11. Среднее ускорение 
а) скалярная величина, равная отношению изменения скорости к тому промежутку времени, за которое это изменение произошло;
б) предел отношения изменения скорости к тому промежутку времени, за которое это изменение произошло;
в) векторная величина, равная отношению изменения скорости к тому промежутку времени, за которое это изменение произошло.
12. Мгновенное значение ускорения 
а) первая производная от скорости 
б) отношение изменения скорости к изменению времени;
в) первая производная от пройденного пути по времени.
13. В координатной форме вектор ускорения 
а) 
б) 
в) 
14. Модуль вектора ускорения 
а)
б)
в)
15. Выбрать правильную последовательность определений ускорений:
а) Тангенциальное, полное, нормальное;
б) Нормальное, полное, тангенциальное;
в) Полное, тангенциальное, нормальное.
16. Выбрать правильное направление вектора полного ускорения 
а) 1; б) 2; в) 3; г) 4;
17. Если 
а) прямолинейным ускоренным;
б) равномерным по окружности;
в) ускоренным по окружности.
18. Если 
а) ускоренное по окружности;
б) равномерное прямолинейное;
в) криволинейное с переменным ускорением.
19. Направление вектора 
а) радиальный вектор;
б) аксиальный вектор;
в) коллинеарный вектор.
20. При вращательном движении твердого тела, если соблюдается условие что 
а) вектор 

б) оба вектора коллинеарные;
в) оба вектора взаимно перпендикулярны.
21. При условии, что 
б) взаимно перпендикулярны;
в) имеют противоположное направление вдоль оси вращения;
22. Диск радиуса R катится равномерно и прямолинейно, без скольжения. Модуль перемещения произвольной точки на ободе диска за один полный оборот равен:
а) 2πR; б)2R; в) 0; г) R.
23. Изменение модуля скорости тела, двигающегося по окружности со скоростью V=5 м/с, при прохождении четверти окружности равно:
а) 4,8 м/с; б) 3,5 м/с; в) 6,2 м/с; г) 1,4 м/с; д) 0 м/с.
24. Траектория движения точки на конце лопасти винта вертолета, равномерно поднимающегося вертикально вверх в системе отсчета связанной с корпусом вертолета, представляет собой:
а) окружность; б) винтовую линию; в) параболу; г) прямую линию.
25. За время t=6 c точка прошла путь, равный половине длины окружности радиусом R=0,8 м. Определить среднюю путевую скорость за это время и модуль вектора средней скорости 
📸 Видео
Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Физика | Равномерное движение по окружностиСкачать

ДВИЖЕНИЕ ПО ОКРУЖНОСТИ: угол поворота и угловая скорость. Ускорение при равномерном движении.Скачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Центростремительное ускорение. 9 класс.Скачать

Физика - движение по окружностиСкачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Урок 12. Равномерное прямолинейное движениеСкачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

1. Кинематика вращательного движенияСкачать

Физика - уравнения равноускоренного движенияСкачать

Скорость и ускорение при равномерном движении по окружности. Видеоурок 6. Физика 9 классСкачать