- Определение угла между прямыми
- Угол между прямыми на плоскости
- Угол между прямыми заданными уравнениями с угловым коэффициентом
- Угол между прямыми через направляющие векторы этих прямых
- Угол между прямыми через векторы нормалей этих прямых
- Угол между прямыми через направляющий вектор и вектор нормали этих прямых
- Примеры задач на вычисления угла между прямыми на плоскости
- Угол между прямыми в пространстве
- Угол между прямыми онлайн
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- Вычисление угла между прямыми на плоскости и в пространстве: формула
- Прямая и ее векторное уравнение
- Общее уравнение для прямой на плоскости
- Формула угла между прямыми
- Параллельность и перпендикулярность прямых
- Задача №1. Перпендикулярные прямые
- Задача №2. Угол пересечения прямых
- 💡 Видео
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Определение угла между прямыми
Видео:14. Угол между прямыми в пространствеСкачать

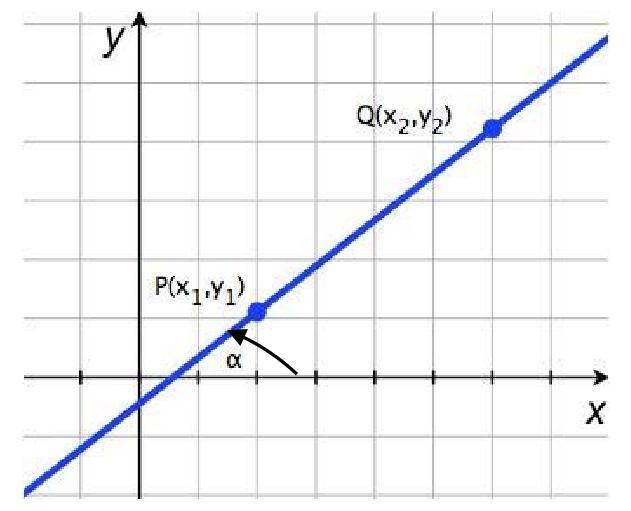
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k 1 — k 2 1 + k 1· k 2
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Видео:Угол между прямыми на плоскостиСкачать

Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k 1 — k 2 1 + k 1· k 2 = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор , для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2 x + 3 y = 0 => y = — 2 3 x ( k 1 = — 2 3 )
x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k 2 = 4 3 )
tg γ = k 1 — k 2 1 + k 1· k 2 = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18
Видео:Угол между прямыми в пространстве. 11 класс.Скачать
Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
Решение: Так как прямые заданы параметрически, то — направляющий вектор первой прямой, направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор .
Преобразуем второе уравнение к каноническому вид.
1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3
3 z — 5 2 = z — 5/3 2/3
Получено уравнение второй прямой в канонической форме
x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3
— направляющий вектор второй прямой.
cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:найти уравнения биссектрис углов между прямымиСкачать

Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:§16 Угол между двумя прямыми на плоскостиСкачать
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
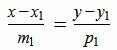 , , | (1.1) |
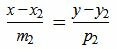 , , | (1.2) |
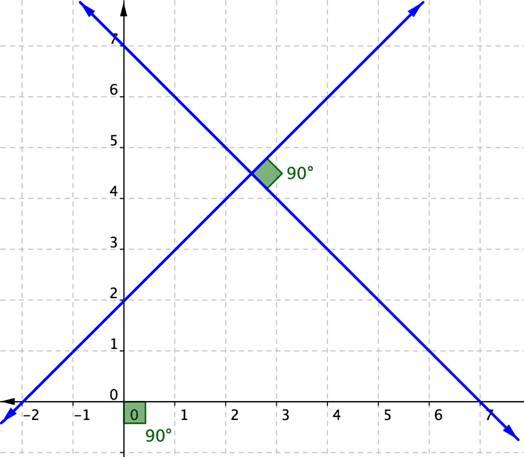
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
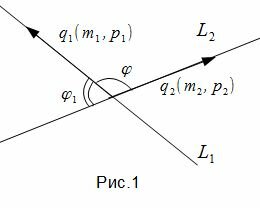 , , |
 , , | (1.3) |
Из выражения (1.3) получим:
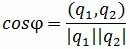 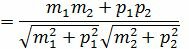 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
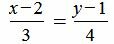 . . | (1.5) |
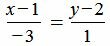 . . | (1.6) |
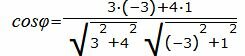 . . |
Упростим и решим:
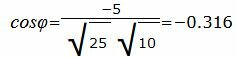 . . |
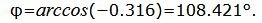 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
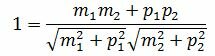 . . | (1.7) |
Сделаем преобразования с выражением (1.7):
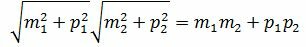 , , |
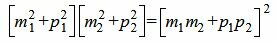 , , |
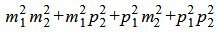 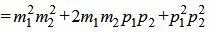 , , |
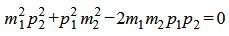 , , |
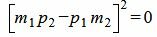 , , |
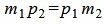 . . | (1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
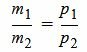 . . | (1.9) |
Пример 2. Определить, параллельны ли прямые
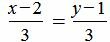 . . | (1.10) |
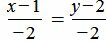 . . | (1.11) |
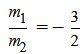 , , 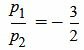 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
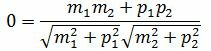 . . | (1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
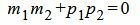 . . | (1.13) |
Пример 3. Определить, перпендикулярны ли прямые
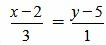 | (1.14) |
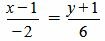 . . | (1.15) |
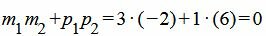 . . | (16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
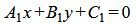 | (1.17) |
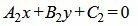 . . | (1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
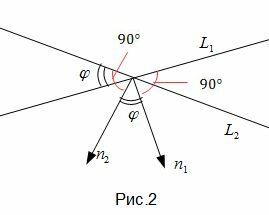 . . |
Из определения скалярного произведения двух векторов, имеем:
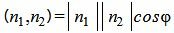 . . | (1.19) |
Из уравнения (19) получим
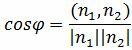 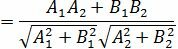 . . | (1.20) |
Пример 4. Найти угол между прямыми
| 5x1−2x2+3=0 | (1.21) |
| x1+3x2−1=0. | (1.22) |
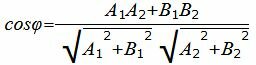 | (23) |
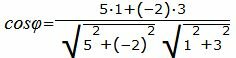 |
Упростим и решим:
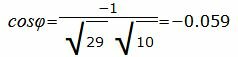 |
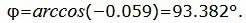 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
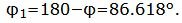 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
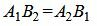 . . | (1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
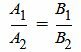 . . | (1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
| 4x+2y+2=0 | (1.26) |
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
| A1A2+B1B2=0. | (1.28) |
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
| 4x−1y+2=0 | (1.29) |
| 2x+8y−14=0. | (1.30) |
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
Видео:Видеоурок "Угол между прямыми"Скачать

2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
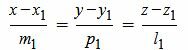 , , | (2.1) |
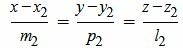 , , | (2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , | (2.3) |
Из выражения (2.3) получим:
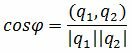 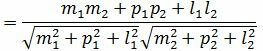 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
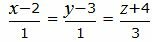 . . | (2.5) |
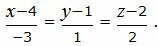 | (2.6) |
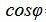 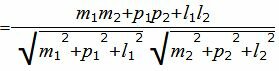 . . |
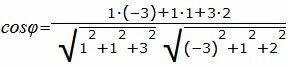 . . |
Упростим и решим:
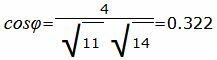 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
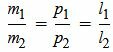 | (2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
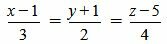 . . | (2.9) |
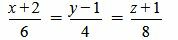 . . | (2.10) |
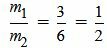 , , 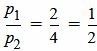 , , 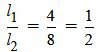 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
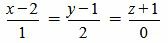 . . | (2.11) |
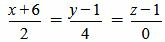 . . | (2.12) |
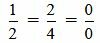 . . | (2.13) |
Выражение (2.13) нужно понимать так:
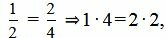 , , 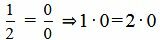 , , 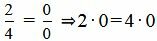 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
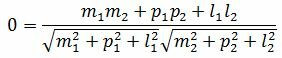 . . | (2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
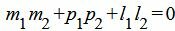 . . | (2.16) |
Пример 3. Определить, перпендикулярны ли прямые
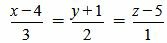 | (2.17) |
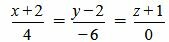 . . | (2.18) |
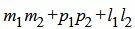 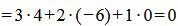 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Видео:9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Вычисление угла между прямыми на плоскости и в пространстве: формула
Типичной геометрической задачей является нахождение угла между прямыми. На плоскости, если известны уравнения прямых, их можно начертить и измерить угол транспортиром. Однако этот способ трудоемок и не всегда возможен. Чтобы узнать названный угол, не обязательно изображать прямые, его можно вычислить. Как это делается, ответит данная статья.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Прямая и ее векторное уравнение
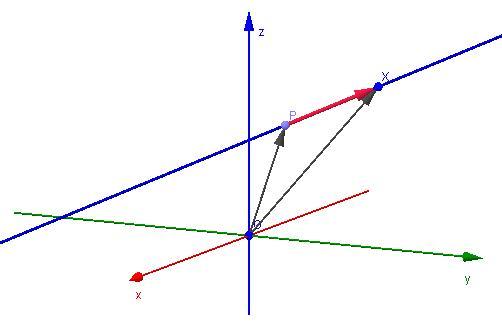
Всякую прямую можно представить в виде вектора, который начинается в -∞ и заканчивается в +∞. При этом вектор проходит через некоторую точку пространства. Таким образом, все вектора, которые можно начертить между двумя любыми точками прямой, будут параллельны друг другу. Это определение позволяет задать уравнение прямой в векторном виде:

(x; y; z) = (x0; y0; z0) + α*(a; b; c)
Здесь вектор с координатами (a; b; c) является направляющим для этой прямой, проходящей через точку (x0; y0; z0). Параметр α позволяет переводить указанную точку в любую другую для этой прямой. Это уравнение интуитивно понятно, и с ним легко работать как в трехмерном пространстве, так и на плоскости. Для плоскости оно не будет содержать координаты z и третьей компоненты направляющего вектора.

Удобство выполнения расчетов и изучения взаимного положения прямых благодаря использованию векторного уравнения связано с тем, что известен ее направляющий вектор. Его координаты применяются для вычисления угла между прямыми и расстояния между ними.
Видео:Угол между прямыми в пространстве. Практическая часть. 11 класс.Скачать

Общее уравнение для прямой на плоскости
Запишем в явном виде векторное уравнение прямой для двумерного случая. Оно имеет вид:
Теперь рассчитаем для каждого равенства параметр α и приравняем правые части полученных равенств:
Раскрывая скобки и перенося все члены в одну сторону равенства, получаем:
A*x + B*y + C = 0, где A = 1/a, B = -1/b, C = y0/b- x0/a
Полученное выражение называется общим уравнением для прямой, заданной в двумерном пространстве (в трехмерном это уравнение соответствует параллельной оси z плоскости, а не прямой).
Если в этом выражении явно записать y через x, то получится следующий вид, известный каждому школьнику:
y = k*x + p, где k = -A/B, p = -C/B
Это линейное уравнение однозначно задает на плоскости прямую. Начертить ее по известному уравнению очень просто, для этого следует по очереди положить x = 0 и y = 0, отметить соответствующие точки в системе координат и провести прямую, соединив полученные точки.
Видео:Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Формула угла между прямыми
На плоскости две прямые могут либо пересекаться, либо быть параллельными друг другу. В пространстве к этим вариантам добавляется также еще возможность существования скрещивающихся прямых. Какой бы вариант взаимного положения этих одномерных геометрических объектов не был реализован, угол между ними всегда можно определить по следующей формуле:
Где v1¯ и v2¯ — это векторы направляющие для прямой 1 и 2 соответственно. В числителе стоит модуль скалярного произведения, чтобы исключить тупые углы и учитывать только острые.
Вектора v1¯ и v2¯ могут быть заданы двумя или тремя координатами, формула для угла φ при этом остается неизменной.
Видео:9. Угол между прямымиСкачать

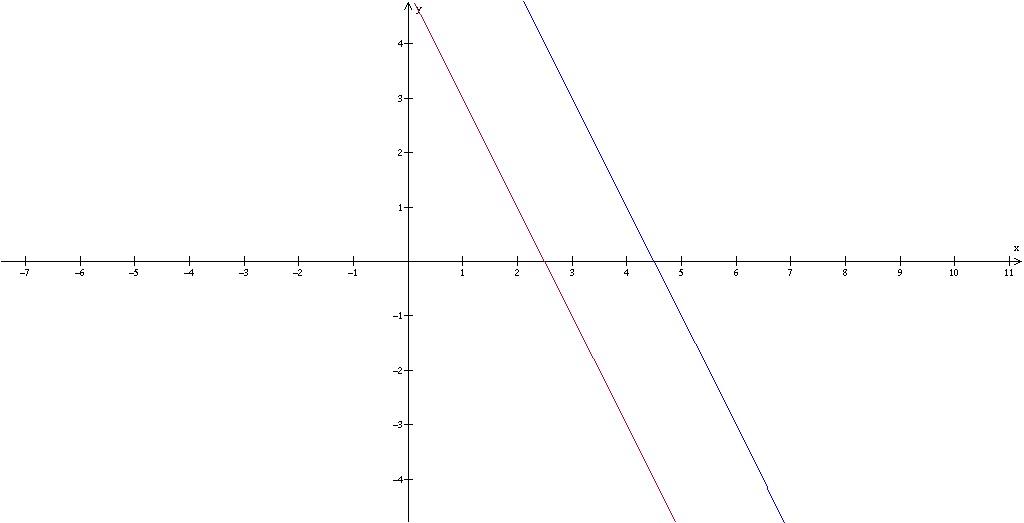
Параллельность и перпендикулярность прямых
Если рассчитанный по формуле выше угол между 2 прямыми равен 0o, то говорят, что они являются параллельными. Чтобы определить, будут прямые параллельными или нет, можно не вычислять угол φ, достаточно показать, что один направляющий вектор может быть представлен через аналогичный вектор другой прямой, то есть:
Здесь q — некоторое действительное число.
Если уравнения прямых заданы в виде:
то параллельными они будут только тогда, когда равны коэффициенты при x, то есть:
Доказать этот факт можно, если рассмотреть, как выражается коэффициент k через координаты направляющего вектора прямой.
Если угол пересечения между прямыми равен 90o, тогда они называются перпендикулярными. Для определения перпендикулярности прямых также не обязательно вычислять угол φ, для этого достаточно рассчитать лишь скалярное произведение векторов v1¯ и v2¯. Оно должно быть равно нулю.
В случае скрещивающихся прямых в пространстве формулой для угла φ тоже можно пользоваться. При этом следует правильно интерпретировать полученный результат. Вычисленный φ показывает величину угла между направляющими векторами прямых, которые не пересекаются и не являются параллельными.
Видео:10 класс, 9 урок, Угол между прямымиСкачать

Задача №1. Перпендикулярные прямые
Известно, что уравнения прямых имеют вид:
Необходимо определить, являются ли эти прямые перпендикулярными.
Как было сказано выше, для ответа на вопрос достаточно провести расчет скалярного произведения векторов направляющих, которым соответствуют координаты (1; 2) и (-4; 2). Имеем:
(1; 2)*(-4; 2) = 1*(-4) + 2*2 = 0
Поскольку мы получили 0, то это означает, что рассматриваемые прямые пересекаются под прямым углом, то есть являются перпендикулярными.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

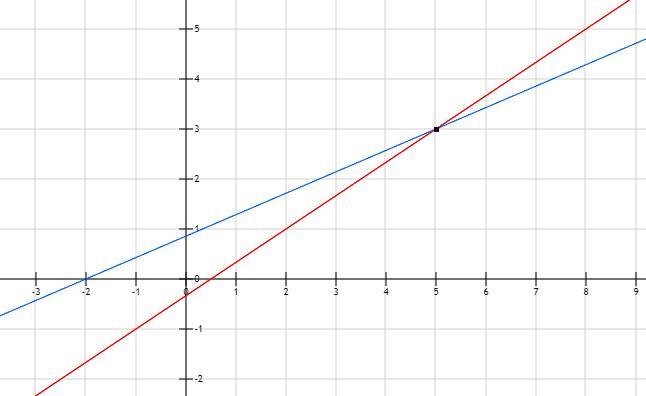
Задача №2. Угол пересечения прямых
Известно, что два уравнения для прямых имеют следующий вид:
Необходимо найти угол между прямыми.
Поскольку коэффициенты при x имеют разную величину, то эти прямые не являются параллельными. Чтобы найти угол, который образуется при их пересечении, переведем каждое из уравнений в векторный вид.
Для первой прямой получаем:
В правой части равенства мы получили вектор, координаты которого зависят от x. Представим его в виде суммы двух векторов, причем координаты первого будут содержать переменную x, а координаты второго будут состоять исключительно из чисел:
(x; y) = (x; 2*x) + (0; — 1) = x*(1; 2) + (0; — 1)
Поскольку x принимает произвольные значения, то его можно заменить на параметр α. Векторное уравнение для первой прямой принимает вид:
(x; y) = (0; — 1) + α*(1; 2)
Те же самые действия проделываем со вторым уравнением прямой, получаем:
(x; y) = (x; -x + 3) = (x; -x) + (0; 3) = x*(1; -1) + (0; 3) =>
Мы переписали в векторном виде исходные уравнения. Теперь можно воспользоваться формулой для угла пересечения, подставляя в нее координаты направляющих векторов прямых:
φ = arccos(|-1|/(√5*√2)) = 71,565o
Таким образом, рассматриваемые прямые пересекаются под углом 71,565o, или 1,249 радиан.
Эту задачу можно было решить иначе. Для этого следовало взять две произвольные точки каждой прямой, составить из них направляющие вектора, а затем воспользоваться формулой для φ.
💡 Видео
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

11 класс, 7 урок, Вычисление углов между прямыми и плоскостямиСкачать

§56 Нахождение угла между прямымиСкачать

94. Угол между прямымиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать