Степень комплексного числа с произвольным целым показателем определяется точно так же, как и для действительного числа.
Для возведения в степень и извлечения корней удобнее всего пользоваться тригонометрической (или показательной) формой записи комплексных чисел.
В предыдущем параграфе было показано, что при умножении двух комплексных чисел их модули умножаются, а аргументы складываются. Используя метод математической индукции (см. гл. 1), можно доказать, что при возведении комплексного числа в степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
Таким образом, при записи в тригонометрической форме
при записи в показательной форме
Очевидно, что оба соотношения представляют собой разные формы записи одной и той же формулы, называемой первой формулой Муавра.
Заметим, что первая формула Муавра верна и для отрицательного целого числа п.
Разберем два примера на применение первой формулы Муавра.
Пример 4.5. Вычислите (1 + /Ч/З) 11 ‘.
Решение. Запишем число 1 + /Ч/З в тригонометрической форме:
Тогда по формуле Муавра получим
Пример 4.6. Выведите тригонометрические формулы синуса и косинуса тройного угла.
Решение. Рассмотрим комплексное число z = cos
3 = cos3q> + /sin 3
Корнем степени п (п е N) из комплексного числа z (z * 0) называется такое число w, что w n = z.
Пусть z — заданное комплексное число и w — некоторый корень степени п из z? Представим z и w в тригонометрической форме:
Воспользовавшись определением корня степени п и первой формулой Муавра, перепишем равенство w n = z в виде
Таким образом, число z двумя способами представлено в тригонометрической форме. Это означает, что в обоих представлениях модуль числа z один и тот же, а аргументы могут отличаться на 2кк, где к е Z. Поэтому имеем систему
Здесь у[г — арифметический корень из положительного числа. Следовательно, всякий корень степени п из числа z имеет вид
Эта формула называется второй формулой Муавра.
Отметим, что все числа wk, получаемые во второй формуле Муавра при к = 0, 1, 2, . п — 1, различны. При всех остальных значениях к е Z корней, отличных от w0, щ, w2, . wn_<, нет.
Таким образом, для z * 0 существует ровно п корней степени п из числа z, причем все корни имеют равные модули и их аргументы
отличаются друг от друга на-, где к е Z.
Замечание. Если числа z и w представлены в показательной форме
то вторая формула Муавра для корней wk степени п из числа z имеет следующий вид:
Пример 4.7. Вычислите V—I.
Решение. Приведенная в условии запись V-T понимается следующим образом. Требуется найти все такие различные комплексные числа wk, что (w*. ) 6 = -1.
Так как модуль г числа z = -1 равен 1, а главный аргумент а = arg(-l) = л, то yfr = 1 и все различные корни wk, согласно второй формуле Муавра, будут иметь вид
Геометрические образы полученных корней представлены на рис. 4.7. ?
- 1. Точки плоскости w0, wl5w2, wn_j, соответствующие корням степени п из комплексного числа z, являются вершинами правильного /7-угольника, вписанного в окружность радиуса yjz, углы между
- 2к argz
векторами для соседних вершин равны —, и argw0 =-.
2. На множестве Ш вводится понятие арифметического корня, т.е. выделяется положительный корень из данного положительного числа. В множестве комплексных чисел все корни степени п равноправны и специального обозначения для какого-то особого корня не вводится.
Рассмотрим алгебраическое уравнение степени п с комплексными коэффициентами:
Коснемся вопросов, связанных с существованием и количеством корней данного уравнения.
На эти вопросы отвечают основная теорема алгебры и ее следствия. Приведем эти утверждения без доказательства.
Основная теорема алгебры. Всякое алгебраическое уравнение степени п > 1 имеет в множестве комплексных чисел по крайней мере один комплексный корень.
Следствие 1. Любой многочлен степени п > 1с комплексными коэффициентами раскладывается в произведение п линейных множителей:
Следствие 2. Любой многочлен степени п > 1с комплексными коэффициентами имеет в множестве комплексных чисел ровно п корней, если считать каждый корень столько раз, какова его кратность.
Следствие 3. Пусть коэффициенты многочлена являются действительными числами. Тогда если ?0 — комплексный корень этого многочлена, то Zq также его корень.
Далее нас будут интересовать только алгебраические уравнения второй степени с комплексными коэффициентами, т.е. уравнения вида
Из основной теоремы алгебры и ее следствий вытекает, что данное уравнение всегда имеет два корня (возможно, эти корни совпадающие).
Для нахождения решений можно применять известную еще со школы формулу корней квадратного уравнения, использующую дискриминант D — Ь 2 — 4ас, который в этом случае является комплексным числом:
Здесь под V7) понимаются все значения корня из комплексного числа D (таких значений всегда два).
Решение. Вычислим вначале дискриминант D = 6 2 — 4 • 1 • 10 = -4. Так как коэффициенты уравнения действительны, то два корня уравнения являются комплексно сопряженными числами. Ставится задача нахождения корней второй степени из числа (-4), т.е. таких чисел wk (к = 0, 1), что(и^) 2 = -4. Очевидно, что w0 = 2/, w, = -2/. Таким образом, решениями исходного алгебраического уравне-
ния являются числа г, ? =-= -3 ± /. ?
Видео:Линии и области на комплексной плоскостиСкачать

Извлечение корня из комплексного числа
Третий урок по комплексным числам. В этом уроке вы узнаете:
Начнём с ключевого определения.
Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

1. Определение комплексного корня
Определение. Корнем $n$-й степени из комплексного числа $z$, где $nin mathbb$, $n gt 1$, называется такое комплексное число $omega $, что
т.е. $n$-я степень числа $omega $ равна $z$.
Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:
Пример. Вычислить $sqrt[3]$ на множестве комплексных чисел.
Очевидно, привычная нам единица является таким корнем, потому что $<^>=-1$. Но есть ещё два корня:
Итого три корня. Как и предполагалось.
Теорема. Для любого комплексного числа $zne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$
Все эти корни считаются по следующей формуле.
Видео:Изобразить область на комплексной плоскостиСкачать

2. Формула корней
Теорема. Пусть комплексное число записано в тригонометрической форме:
[z=left| z right|cdot left( cos varphi +isin varphi right)]
Тогда все корни степени $n$ из этого числа можно найти по формуле:
По сути, эта теорема является обратной к формуле Муавра:
Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:
- Перевести комплексное число в тригонометрическую форму;
- Записать общую формулу корня степени $n$;
- Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
- Получим $n$ комплексных корней. Вместе они и будут ответом.
В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $zne 0$.
Представим число $-8i$ в тригонометрической форме:
[begin -8i &=0+left( -8 right)cdot i= \ & =8cdot left( 0+left( -1 right)cdot i right)= \ & =8cdot left( cos left( -frac right)+isin left( -frac right) right) end]
Запишем формулу корней в общем виде:
[sqrt[3]=2cdot left( cos left( -frac right)+isin left( -frac right) right)=sqrt-i]
В ответе нужно указать все три числа: $-2i$; $sqrt-i$; $-sqrt-i$.
Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $left$, то корни начнут повторяться, и ничего нового мы не получим.
Видео:Решение уравнений на комплексной плоскостиСкачать

3. Геометрическая интерпретация
Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $zne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=sqrt[n]$. Более того: эти точки образуют правильный $n$-угольник.
Отметить на комплексной плоскости все числа вида $sqrt[3]$.
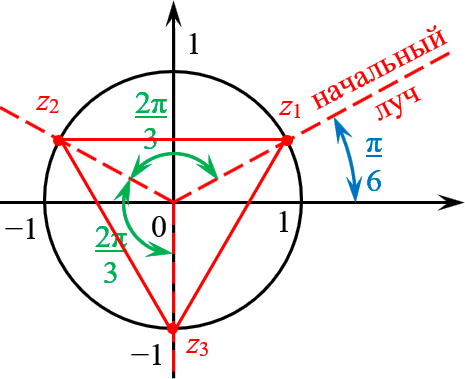
Представим число $z=i$ в тригонометрической форме:
[begin z & =1cdot left( 0+icdot 1 right)= \ & =1cdot left( cos frac+isin frac right) end]
Формула комплексных корней:
[sqrt[3]=1cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)]
Это три точки $<_>$, $<_>$ и $<_>$ на окружности радиуса $R=1$:
Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $/;$.
Рассмотрим более сложный пример:
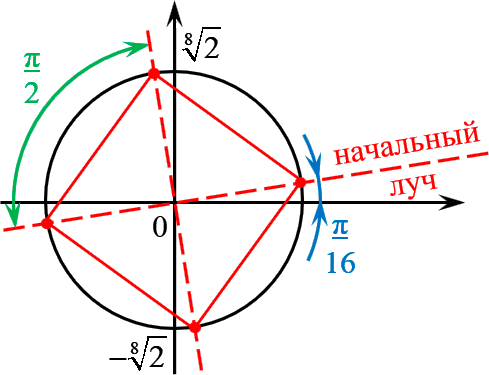
Отметить на комплексной плоскости все числа вида $sqrt[4]$.
Сразу запишем формулу корней с выделением начального луча:
[sqrt[4]=sqrt[8]cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)]
Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=sqrt[8]$, начальный луч $/;$:
И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $/;$.
Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:
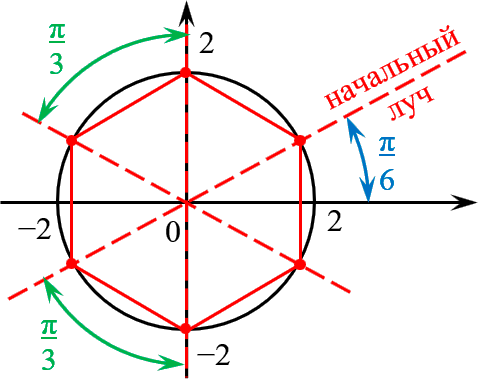
Отметить на комплексной плоскости все числа вида $sqrt[6]$.
Формула корней с выделением начального луча:
[sqrt[6]=2cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)]
Получили правильный шестиугольник со стороной 2 и начальным лучом $/;$.
Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $zne 0$:
- Перевести число в тригонометрическую форму;
- Найти модуль корня: $sqrt[n]$ — это будет радиусом окружности;
- Построить начальный луч с отклонением $varphi =/;$;
- Построить все остальные лучи с шагом $/;$;
- Получим точки пересечения лучей с окружностью — это и есть искомые корни.
Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $varphi $ — стандартные «табличные» углы вроде $/;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)
Видео:Область на комплексной плоскости arg z = pi/2Скачать

4. Почему корней всегда ровно n
С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.
Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:
Последовательно подставим в эту формулу указанные значения параметра $k$:
Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:
Поскольку синус и косинус — периодические функции с периодом $2pi $, $<_>=<_>$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.
Видео:Как найти множество точек комплексной плоскости?Скачать

5. Выводы
Ключевые факты из урока.
Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $omega $, что $<^>=z$.
Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $omega =sqrt[n]$.
Замечание. Если $zne 0$, таких чисел корней будет ровно $n$ штук.
Алгоритм нахождения корней состоит из двух шагов.
Шаг 1. Представить исходное число в тригонометрической форме:
[z=left| z right|cdot left( cos varphi +isin varphi right)]
Шаг 2. Воспользоваться формулой Муавра для вычисления корней:
Все полученные корни лежат на окружности радиуса $sqrt[n]$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $/;$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.
Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».
Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)
Видео:Окружности на комплексной плоскостиСкачать
Методичесое пособие «Комплексные числа» для системы ДО и профессиональных классов
Разделы: Математика
Во многих разделах математики и ее приложениях невозможно ограничиться лишь рассмотрением действительных чисел. Например, решение уравнений типа х 2 +х+1=0, х 2 +1=0.
Для их решения надо расширить множество действительных чисел и таким расширением являются комплексные числа.
Комплексные числа часто называют мнимыми. Это название объясняется тем, что, хотя стали употребляться еще в XVI веке, они долго продолжали называться даже выдающимися математиками чем-то реально не существующими, мнимыми в буквальном смысле. Одному из создателей дифференциального и интегрального исчисления, немецкому математику Г. Лейбницу (1646–1716) принадлежат, например, такие слова:
“Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием”.
Но уже во времена К. Гаусса (1777–1855) было дано геометрическое истолкование комплексных чисел как точек плоскости. Трудами выдающихся математиков XIX века О. Коши, Б. Римана, К. Вейерштрасса на базе комплексных чисел была построена одна из самых красивых математических дисциплин – Теория функций комплексной переменной.
II. Определение комплексного числа.
Комплексными числами называют выражения вида a +bi , где a и b – действительные числа, i – некоторый символ и i 2 =-1, для которых следующим образом вводятся понятия равенства и операции сложения и умножения:
Комплексные числа часто обозначают одной буквой, причем обычно используют буквы z и ω.
Равенство z=a+bi называют алгебраической формой записи числа z.
Частное чисел z2 и z1 при условии z1≠0 понимается следующее комплексное число:
Заметим что число 0+bi называют чисто мнимым и записывают bi,
Если b=0, то число a просто действительное.
Действительная часть числа z=a+bi обозначается Rez.
Мнимая часть числа z обозначается Imz.
Найти сумму и произведение чисел z1=2+5i ,z2=-1+7i.
Найти разность и частное чисел z2=2+5i , z1=– 1+6i
Пример 3 i 3 =i*i*i=-i, i 4 =i*i*i*i=1.
III. Геометрическая интерпретация комплексных чисел. Модуль и аргументы комплексного числа.

Рис.1
Хорошо известно, что между множеством действительных чисел и множеством точек прямой можно установить взаимно однозначное соответствие. Геометрическую интерпретацию можно использовать и при изучении комплексных чисел.
Каждому комплексному числу z=a+bi можно поставить в соответствие точку M(a,b) координатной плоскости.
Сама координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, а ось ординат мнимой осью.
Число z=a+bi есть вектор 
При сложении z1 и z2 складываются их действительные и мнимые части. При сложении 
Таким образом сумма (разность) комплексных чисел геометрически ,векторов, соответствующих слагаемым комплексных чисел.
Модулем комплексного числа называется длина вектора соответствующего этому числу и обозначается │ Z│.


Аргументы комплексного числа.
Комплексные числа имеющие один и тот же модуль │ Z│ = r, соответствуют, очевидно, точкам плоскости расположенными на окружности радиуса r с центром в точке z=0.

Рис. 2
Определение. Аргументом комплексного числа z≠0 называется величина угла между положительным направлением действительной оси и вектором 
Любые два аргумента комплексного числа отличаются друг от друга слагаемым кратным 2π.
IV. Тригонометрическая форма записи комплексного числа. Операции над комплексными числами.
Помимо алгебраической формы используются и другие формы записи комплексных чисел – тригонометрическая форма и показательная форма записи комплексных чисел.
Рассмотрим тригонометрическую форму записи.
Действительная и мнимая части комплексного числа z=a+bi выражаются через его модуль │ Z│ =r и аргумент φ следующим образом (рис.2).
Поэтому комплексное число z может быть записано в следующем виде: z= r(cos φ + isin φ )
Такая запись называется тригонометрической формой записи.
Для того чтобы перейти от алгебраической формы z=a+bi к тригонометрической форме записи числа, достаточно найти его модуль и один из аргументов. Модуль определяется по формуле:
Записать число z=1-I в тригонометрической форме.
Одним из решений этой системы будет:
но эти записи будут являться алгебраической, а не тригонометрической формой записи комплексного числа.
Умножение и деление комплексных чисел записанных в тригонометрической форме.
Таким образом: модуль произведения двух комплексных чисел равен произведению модулей, сумма аргументов есть аргумент произведения.
Следовательно, модуль частного двух комплексных чисел равен частному этих модулей, разность аргументов делимого и делителя является аргументом частного.
Модуль произведения n комплексных чисел равен произведению всех сомножителей, сумма аргументов всех сомножителей является аргументом произведения. Отсюда, как частный случай, получается формула, которая носит название формулы Муавра.
(r(cosφ+isinφ)) n =r n (cosnφ+isinφn)
Перейдем к операции извлечения корня из данной степени комплексного числа.
Число z является корнем степени n из числа ω, если z n =ω.
Из данного определения вытекает, что каждое решение уравнения z n =ω является корнем n из числа ω.
Пусть ω≠0, тогда z=r( cosφ + isinφ ), ω =s( cosψ + isinψ )
Уравнение z n = ω запишем в виде: r n ( cosnφ + isinφn )=s( cosψ + isinψ )
Два комплексных числа равны, когда равны их модули, а аргументы различаются слагаемым кратным 2π, то есть r n =s и nφ=ψ+2π k
как пара комплексных чисел i и –i.
Найти все значения 
Точки z0,z1,z2,z3 есть вершины квадрата вписанного в окружность радиуса 2.
V. Квадратные уравнения.
Рассмотрим уравнение: ax 2 +bx+c=0, a≠0
a,b,c – действительные числа , тогда D=b 2 -4ac дискриминант и решение задается по формуле: x= 
Решим это уравнение в комплексных числах, тогда, если D˂0, мы получаем решение в комплексных числах:
: z=
Над множеством комплексных чисел справедлива основная теорема алгебры : алгебраическое уравнение n – степени имеет ровно n корней.
VI. Комплексная степень числа e. Показательная форма записи.
Возведем e в степень z, где z=x+iy.e z =e x e iy =e x (cosy+isiny).
Доказательство данной формулы основано на разложении элементарных функций в ряд Тейлора в окрестности нуля.
- А.В. Бицадзе “Основы теории аналитических функций”. М, “Наука”, 1984 г.
- Г.Н. Яковлев и др. “Алгебра и начала анализа”. М, “Наука”, 1981 г.
🎥 Видео
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Кольцо на комплексной плоскостиСкачать
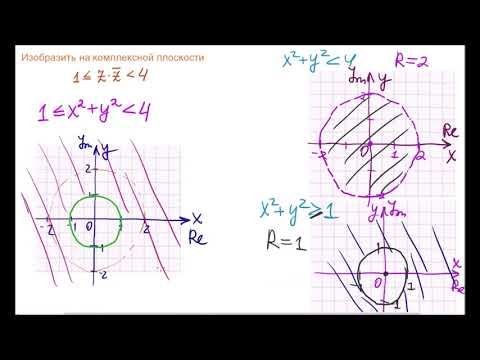
10 класс, 33 урок, Комплексные числа и координатная плоскостьСкачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

z=mod z. Найти множество комплексных точекСкачать
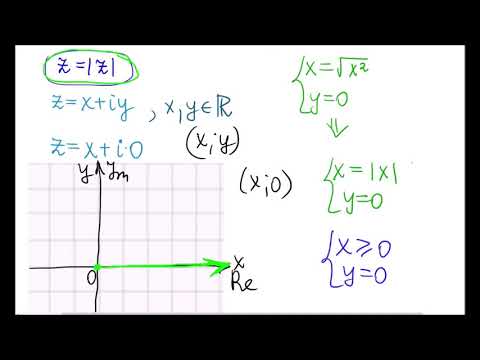
Комплексные числа в уравненияхСкачать

Отображение на комплексной плоскости (старая задача о двух картах)Скачать

Найдите все значения корня из комплексного числа ∛-125i ★ Извлечение корня из комплексного числаСкачать
Построение областей по заданным условиямСкачать

Множества на комплексной плоскости. Связное множество. Односвязная область. Граница. Круг сходимостиСкачать

ТФКП. Линии и области на комплексной плоскости #shorts #mathСкачать