Точка выбирается наудачу в квадрате какова вероятность что уравнение будет иметь действительные (7 видео)

Содержание

Какова вероятность того, что корни этого уравнения будут действительными числами?
Задача 162 Точка выбирается наудачу в квадрате
Случайное квадратное уравнение
🌟 Видео

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Какова вероятность того, что корни этого уравнения будут действительными числами?

Коэффициенты р и q квадратного уравнения х 2 + рх + q = 0 выбирают наудачу на отрезке [0; 2]. Какова вероятность того, что корни этого уравнения будут действительными числами?

Решение. Обозначим событие: А – корни данного уравнения будут действительными числами. Найдем вероятность события А, применив формулу р(А) = mesD / mesΩ. Пусть коэффициенты р и q квадратного уравнения ‒ наудачу взятые числа. Их возможные значения: 0 2 – 4q > 0, откуда следует, что q ≤ р 2 / 4.

Построим границы области, которой принадлежат точки плоскости, удовлетворяющие условиям:

Граничные прямые р = 0, р = 2, q = 0, q = 2 являются сторонами квадрата, ограничивающего область возможных значений р и q. Граничная кривая q = р 2 /4 представляет собой параболу. Решениями составленной системы неравенств являются координа-ты всех точек плоскости, расположенных на рис. 1.14 заштрихованной области, то есть между граничными линиями р = 0, q = 2, q = р 2 /4 и на самих этих линиях. Точки плоскости, принадлежащие заштрихованной области, характеризуют исходы испытания, благоприятст-вующие событию А. Площадь заштрихованной области равна

Таким образом, вероятность события А равна р(А) = S_g / S_G = 1 / 6.

Видео:Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Задача 162 Точка выбирается наудачу в квадрате

Тип работы: Задача

Предмет: Математическая статистика

Статус: Выполнен

Год работы: 2020

Страниц: 1

Оригинальность: 90% (antiplagiat.ru)

Формат: Microsoft Word

Цена: 60 руб.

Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

С помощью этой страницы вы сможете научиться решать задачи по математической статистике:

Другие похожие задачи:

Описание работы:

Задача 162 Точка (ξ, η) выбирается наудачу в квадрате [0, 1]2. Какова вероятность того, что уравнение x2 + ξx + η = 0 имеет а) действительные корни; в) корни разного знака?б) положительные корни;

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

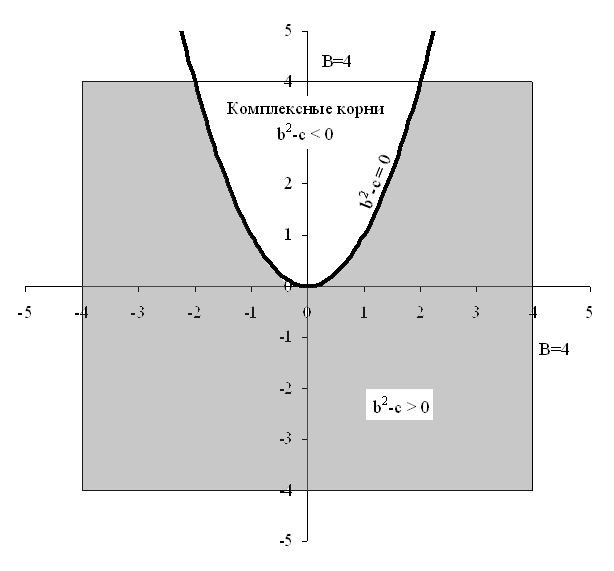
Случайное квадратное уравнение

Какова вероятность того, что корни квадратного уравнения x 2 + 2bx + c = 0 вещественны?

Для того чтобы вопрос задачи имел смысл, предположим, что точка (b, c) равномерно распределена на квадрате с центром в начале координат и стороной 2B (рис. 1). Решим задачу при фиксированном B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

Рис. 1. Серая область отвечает случаю вещественных корней

Для того чтобы уравнение имело вещественные корни, необходимо и достаточно, чтобы
b 2 — c ≥ 0.

На приведенном рисунке изображена парабола b 2 = c и показана область, где наше уравнение имеет вещественные корни для B = 4.

Нетрудно подсчитать, что площадь незаштрихованной области равна 4/3∙B 3/2 (при B ≥ 1), а площадь всего квадрата, конечно, равна 4B 2 . Следовательно, вероятность того, что корни комплексные, равна 1/3∙√ B . При B = 4 ответ равен 1/6. С ростом B 1/√ B стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.

Следует заметить, что эта задача отличается от такой же задачи, связанной с уравнением ax 2 + 2bx + c = 0. Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.

Публикуется по работе: Пятьдесят занимательных вероятностных задач с решениями. Ф.Мостеллер, перев. с англ., издание второе. М. Наука, 1975, 112 с.

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди «Не укради»