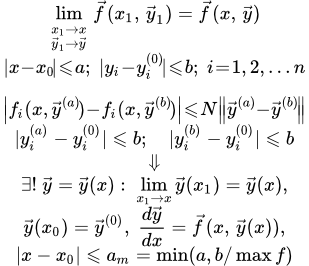Теорема о существовании и единственности решения системы линейных уравнений

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 13.4. Существов. и единств. решения ДУСкачать

Теорема существования и единственности решения системы дифференциальных уравнений

Здесь мы рассматриваем теорему существования и единственности решения системы дифференциальных уравнений с неизвестными функциями от переменной :
(1.1) ;
(1.2) ;
.
(1.n) .

Формулировка и доказательство этой теоремы является непосредственным обобщением теоремы для уравнения первого порядка, которое рассмотрено на странице “Теорема существования и единственности решения ДУ первого порядка”.

Видео:Теорема о существовании фундаментальной системы решений системы линейных однородных уравнений.Скачать

Векторная форма записи

Поскольку уравнения (1.1) – (1.n) однотипны, то мы применим векторную форму записи. Это позволит сократить объем выкладок и сделает доказательство более ясным.

Совокупность неизвестных функций мы будем обозначать одним вектором . Совокупность функций от независимой переменной и от зависимых функций мы обозначим как
.

То есть совокупность из величин мы будем обозначать вектором . Равенство

будет обозначать систему из уравнений:
,
где .

Под нормой вектора мы будем понимать сумму модулей его компонент:
.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Формулировка теоремы

Пусть дана система дифференциальных уравнений:
(1)
с начальными условиями
(1.0) .
Пусть – непрерывных функций от переменных в замкнутой области :

и, следовательно, ограничены некоторым положительным значением :
(2) .
И пусть функции удовлетворяют в области условию Липшица:
(3) ,
где – положительное число.
Тогда существует единственное решение системы (1):
,
удовлетворяющее начальным условиям , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Условие Липшица

Условие Липшица имеет вид:
(3) .
или в развернутом виде:
(3.1) ,
где – положительное число;
, и – любые значения из области .

Если условие Липшица выполняется и в некоторой точке существует частная производная , то она ограничена по модулю значением .
Для доказательства положим в (3.1) для всех . Тогда (3.1) примет вид:
.
Перейдем к пределу :
.

Если в области функции имеют непрерывные частные производные , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частные производные непрерывны в замкнутой области, то они ограничены:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой компоненты принадлежат интервалам между и :
.
Тогда:

.

Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Доказательство существования решения

Приведем исходную систему (1) с начальными условиями (1.0) к системе интегральных уравнений. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем каждое уравнение по от до :
;
Подставим начальные условия . В результате получим систему интегральных уравнений:
(4) .

Покажем, что система интегральных уравнений (4) эквивалентна дифференциальным уравнениям (1) с начальными условиями (1.0). Для этого нужно показать, что из (1) и (1.0) следует (4) и из (4) следует (1) и (1.0). То, что из (1) и (1.0) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.0). Для этого подставим в (4) . Получим начальные условия (1.0). Продифференцировав обе части системы (4) по , получаем (1).

Далее мы пытаемся найти решение уравнений (4) с помощью последовательных приближений. Для этого определяем ряд векторов функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.m) .
Функции непрерывны, потому что интеграл есть непрерывная функция от верхнего предела. Мы предполагаем, что при , стремится к решению системы (4):
(6) ,
где – решение системы (4). Если мы докажем это, то мы докажем существование решения.

Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет системе (4):
.

1) Доказательство существования предела y (m) при m стремящемся к бесконечности

Сведем последовательные приближения (5.1) – (5.m) к суммам рядов. Для этого пишем:

.
Таким образом нам нужно доказать, что ряды
(7)
сходятся при .

Сначала покажем, что при , компоненты последовательных приближений принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.

Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.

Далее, по индукции, поскольку принадлежит интервалу , то и
.
Отсюда
.

Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7).

Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):

;
(8.2) .

Далее применим метод индукции. Пусть
(8.m) .
Тогда

;
(8.m+1) .
Итак, поскольку (8.m) справедливо для и из (8.m) следует (8.m+1), то (8.m) выполняется для любых .

Запишем -й ряд (7) в виде:
(7.i) ,
где .
Применим (8.m) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.i), кроме первого, ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.i), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.i) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.i) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .

2) Доказательство того, что Y является решением (4)

Рассмотрим уравнение (5.m):
(5.m) .
Докажем, что при , это уравнение стремится к уравнению
(11) .

В силу (10) левая часть уравнения (5.m) стремится к .

Теперь покажем, что
.

Перепишем правую часть (5.m):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.

Оценим абсолютную величину последнего члена:

.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
(12) .
Пусть есть наибольшее из чисел . Тогда (12) выполняется для всех и для всех .
Тогда
.
Поскольку произвольно, то

Поэтому
.
То есть при уравнение
(5.m) .
принимает вид
(11) .

Видео:Теорема о количестве решений системы линейных уравненийСкачать

Доказательство единственности решения

Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Тогда .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.

Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .

Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .

Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).

Сделаем оценку, применяя уравнение (4) и условие Липшица:

.
Итак, мы получили оценку:
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.

Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 20-06-2016

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:3. Условия существования и единственности решения задачи КошиСкачать

Системы линейных уравнений

Обозначим через $ mathbb A_ $ любое из множеств $ mathbb Q_, mathbb R_ $ или $ mathbb C_ $.

Примеры систем уравнений над $ mathbb R $.

Относительно числа $ m_ $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_ $. Если $ m_>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных $ x_1=alpha_,dots, x_n = alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.

Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:

1. система совместна и имеет единственное решение;

2. cистема совместна и имеет бесконечное множество решений;

3. cистема несовместна.

При этом все решения будут находиться в том же множестве $ mathbb A_ $, что и коэффициенты системы.

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Матричная форма записи

Для системы линейных уравнений относительно переменных $ x_1,x_2,dots,x_n $ $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_2,\ dots & & & & dots \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_m. end right. $$ матрицей системы называется матрица $$ A=left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right)_ ; $$ cтолбец $$ = left( begin b_ \ b_ \ vdots \ b_ end right) $$ называется столбцом правых частей системы, а столбец $$ X= left( begin x_ \ x_ \ vdots \ x_ end right) $$ — столбцом неизвестных. Используя правило умножения матриц, систему можно записать в матричном виде: $$ AX= . $$ Любое решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы можно также записать в виде столбца: $$ X=left( begin alpha_1 \ vdots \ alpha_n end right) in mathbb A^n . $$ Матрица, составленная из всех коэффициентов системы уравнений: $$ [A mid mathcal B ]= left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ , $$ т.е. конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ называется расширенной матрицей системы л.у.

Видео:Решение системы уравнений методом ГауссаСкачать

Исключение переменных (метод Гаусса)

метода достаточно проста.

Пример. Решить систему уравнений $$ left< begin 2x_1&-3x_2&-x_3&=3 \ 4x_1&-3x_2&-5x_3&=6 \ 3x_1&+5x_2&+9x_3&=-8 end right. $$

Решение. Выразим из первого уравнения $ x_ $ $$ x_1=frac x_2+frac x_3 + frac $$ и подставим в оставшиеся уравнения $$ 4 left(frac x_2+frac x_3 + fracright) -3,x_2-5,x_3=6 <coloriff > 3x_2-3x_3 = 0 $$ $$ <coloriff > x_2-x_3=0 ; $$ $$ 3 left(frac x_2+frac x_3 + fracright) +5x_2+9x_3=-8 <coloriff > frac x_2 +fracx_3=-frac $$ $$ <coloriff > 19x_2 +21x_3=-25 . $$ Два получившихся уравнения не зависят от неизвестной $ x_ $ — она оказалась исключенной из этих уравнений. Иными словами, мы получили новую подсистему уравнений $$ left< begin x_2&-x_3&=0 \ 19x_2&+21x_3&=-25, end right. $$ которой должны удовлетворять неизвестные $ x_ $ и $ x_ $. Продолжаем действовать по аналогии: выразим из первого уравнения $ x_ $ через $ x_ $: $$x_2=x_3 $$ и подставим во второе: $$ 40 x_3 =-25 iff x_3=-frac . $$ Итак, значение одной компоненты решения получено. Для нахождения оставшихся подставим значение $ x_ $ в полученные по ходу решения соотношения: $$ x_2=x_3=-frac Rightarrow x_1=frac x_2+frac x_3 + frac=frac . $$

Ответ. $ x_=1/4, x_2=-5/8, x_3=-5/8 $.

Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.

Исключение переменных

Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:

1. перестановка двух уравнений;

2. умножение обеих частей уравнения на любое отличное от нуля число;

3. прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений $$ begin a_x_1 +a_x_2+ ldots+a_x_n &=&b_j,\ a_x_1 +a_x_2+ ldots+a_x_n &=&b_k end $$ заменяется парой $$ begin (a_+ <colorlambda > a_) x_1 &+ (a_+ <colorlambda > a_) x_2 &+ ldots &+ (a_+ <colorlambda > a_) x_n &=&b_j + <colorlambda > b_k, , \ a_x_1 &+a_x_2&+ ldots &+a_x_n &=&b_k , . end $$

Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.

Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.

Предположим, что первое уравнение системы содержит явно неизвестную $ x_ $, т.е. $ a_^ ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_/a_^ $. Получим $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_2 — frac<a_><a_> b_1 , $$ Аналогичное преобразование — вычитание из третьего уравнения системы первого, умноженного на $ a_/a_^ $, позволяет исключить $ x_ $ из этого уравнения, т.е. заменить его на $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_3 — frac<a_><a_> b_1 . $$ Продолжаем процесс далее. В конечном итоге исключаем $ x_ $ из всех уравнений кроме первого: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ &a_^x_2&+ ldots&+a_^x_n &=b_2^,\ &dots & & & dots \ &a_^x_2&+ ldots&+a_^x_n &=b_m^. end right. npu begin a_^ &= & displaystyle a_ — frac<a_a_><a_> ,\ b_j^ &= & displaystyle b_j — frac<a_b_1><a_> . end $$ Полученная система эквивалентна исходной системе, однако она имеет более простой вид: в ней выделилась подсиcтема $$ left< begin a_^x_2&+ ldots&+a_^x_n &=b_2^,\ dots & & & dots \ a_^x_2&+ ldots&+a_^x_n &=b_m^, end right. $$ которая не зависит от переменной $ x_ $. К этой новой подсистеме можно применить те же рассуждения, что и к исходной системе, поставив теперь целью исключение переменной $ x_ $.

Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим, где он может прерваться. Может так случиться, что очередная, $ ell_ $-я подсистема имеет коэффициент $ a_^ $ равным нулю, что не позволит алгоритму идти дальше — т.е. исключить переменную $ x_^ $ из оставшихся уравнений (в принципе, такое могло случиться уже на первом шаге, если бы коэффициент $ a_^ $ был бы равен нулю). Возможные варианты дальнейших действий:

1. если хотя бы один коэффициент при $ x_^ $ в одном из оставшихся уравнений отличен от нуля: $ a_^ne 0^ $, то это уравнение переставляется с $ ell_ $-м;

2. если при всех $ jge ell^ $ коэффициенты $ a_^ $ равны нулю, то переменная $ x_^ $ не входит ни в одно оставшееся уравнение, и можно перейти к исключению переменной $ x_^ $.

Поскольку число переменных конечно, то алгоритм исключения должен завершиться за конечное число шагов. Чем он может завершиться? Окончательная система должна иметь вид: $$ left< begin a_x_1 +&a_x_2&+ ldots& +a_<1 >x_& +a_ <1 ,+1>x_<+1>&+ ldots + & a_x_n &=b_1,\ &a_^x_2&+ ldots& +a_<2 >^ x_& +a_<2 ,+1>^ x_<+1>&+ ldots + & a_^ x_n &=b_2^,\ & & ddots & & & & & dots \ & & & a_ <>^<[-1]>x_ & + a_ <, +1>^<[-1]>x_<+1>& + ldots + & a_ <,n>^<[-1]>x_n &=b_^<[-1]>, \ & & & & & & 0 &=b_<+1>^<[-1]>, \ & & & & & & dots & \ & & & & & & 0 &=b_^<[-1]>, \ end right. $$ при $ le n_ $. Заметим, что все коэффициенты этой системы будут принадлежать тому же множеству, что и коэффициенты исходной системы.

Предположение . Мы будем считать, что каждое из первых $ _ $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.

Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.

Исторический комментарий о Гауссе ☞ ЗДЕСЬ.

Установление множества решений

Теорема. Если хотя бы одно из чисел $ b_<+1>^<[-1]>,dots , b_^<[-1]> $ отлично от нуля, то исходная система линейных уравнений будет несовместной.

Для простоты мы будем иллюстрировать наши рассуждения на системах л.у. над $ mathbb R_ $, в этом же множестве искать решения. Каждое из преобразований метода Гаусса будем обозначать $ to_ $.

Пример. Решить систему л.у.

$$ left< begin x_1&+x_2&-3, x_3 =& -1 \ 2,x_1&+x_2&-2, x_3 =& 1 \ x_1&+x_2&+ x_3 =& 3 \ x_1&+2,x_2&-3, x_3 =& 1. end right. $$

Решение. $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &x_2&=& 2 end right. to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&4, x_3=& 5 end right. to $$ $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&0=& 1 end right. $$ Последнее равенство абсолютно противоречиво.

Ответ. Система несовместна.

Пусть теперь $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $. Возможны два случая: $ =n_ $ и $ предположения , имеем $ a_^ ne 0 $. Но тогда, поскольку система является конечной стадией прямого хода метода Гаусса, то и все коэффициенты $ a_^, dots, a_^, a_ $ должны быть отличны от нуля — в противном случае метод Гаусса не остановился бы на системе такого вида; он называется треугольным: Из последнего уравнения системы можно однозначно установить значение $ x_ $: $$x_n=b_n^ big/ a_^ .$$ Далее, подставляя это значение в $ (n-1) $-е уравнение системы, выражаем $ x_ $: $$ x_= frac<b_^ — a_^x_>< a_^>= frac< b_^ — a_^ b_n^ Big/ a_^>< a_^> . $$ Подставляем полученные значения для $ x_ $ и $ x_ $ в $ (n-2)_ $-е уравнение системы, выражаем $ x_ $, и т.д., в конце концов приходим к первому уравнению, из которого выражаем $ x_ $ если ранее уже получены выражения для $ x_2,dots,x_ $.

Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е. $ mathfrak r = n_ $ и $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $, то исходная система линейных уравнений имеет единственное решение.

Пример. Решить систему л.у.

$$ left< begin x_1&+3,x_2&+ x_3 =&5 \ 2,x_1&+x_2&+ x_3 =& 2 \ x_1&+x_2&+ 5,x_3 =& -7 \ 2,x_1&+3,x_2&-3, x_3 =& 14. end right. $$

Ответ. $ x_1=1,, x_=2,, x_3=-2 $ .

Исследуем теперь случай $ 1) : На основании предположения , в $ $-м уравнении этой системы имеется хотя бы один ненулевой коэффициент в левой части, пусть $ a_ <>^<[-1]>ne 0 $ — первый из них. Если $ =n $, то из этого уравнения однозначно определится $ x_ $ $$ x_n=alpha_n = b_^<[-1]> big/ a_ <n>^<[-1]> . $$ Если же $ предположения , в этом уравнении имеется хотя бы один ненулевой коэффициент в левой части; пусть $ a_<-1, >^<[-2]>ne 0_ $ — первый из них. Поскольку мы преположили, что система является конечной стадией прямого хода метода Гаусса, то $ по крайней мере две переменные, значения которых еще не были зафиксированы на предыдущих шагах. Это следует из предположения, что число уравнений $ _ $ меньше числа неизвестных $ n_ $. Такое уравнение допускает бесконечное число решений, любое из которых в ходе дальнейших шагов может быть «доделано» до решения системы.

Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е. $ mathfrak r 2) матрицы $ A_ $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков; образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.

Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Формулы Крамера

Рассмотрим систему линейных уравнений с квадратной матрицей $ A_ $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.

Теорема. Cистема

$$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&b_1\ a_x_1 +a_x_2+ldots+a_x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_n endright. $$ имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $$ left| begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right| ne 0 . $$ В этом случае решение можно вычислить по формулами Крамера 3) : $$ x_k =frac<det left[ A_|dots|A_||A_|dots|A_ right]> quad npu quad kin . $$ Для получения значения $ x_ $ в числитель ставится определитель, получающийся из $ det A_ $ заменой его $ k_ $-го столбца на столбец правых частей ( здесь $ | $ означает конкатенацию).

Доказательство ☞ ЗДЕСЬ

Пример. Решить систему уравнений

$$ left<begin 2x_1& +3x_2&+11x_3&+5x_4 &=& color2,\ x_1& +x_2&+5x_3&+2x_4 &=& color1 ,\ 2x_1& +x_2&+3x_3&+2x_4 &=&color,\ x_1& +x_2&+3x_3&+4x_4 &=&color. endright. $$

Решение. $$ x_1=frac<left|begin color2 & 3&11&5 \ color1 & 1&5&2 \ color& 1&3&2 \ color & 1&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=-2, x_2=frac<left|begin 2& color2&11&5 \ 1& color1&5&2 \ 2& color&3&2 \ 1& color&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=0, dots $$ Найдите оставшиеся компоненты решения. ♦

Решение системы линейных уравнений с квадратной матрицей $ A_ $ является непрерывной функцией коэффициентов этой системы при условии, что $ det A_ ne 0 $.

Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.

Еще один способ решения системы основан на построении обратной матрицы: $$ AX= quad Rightarrow quad X=A^ . $$ Этот способ малоэффективен при фиксированных числовых $ A_ $ и $ _ $.

Найти достаточное условие существования общего решения систем уравнений:

$$ A_1 X = _1 quad u quad A_2 Y = _2 , $$ при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Теорема Кронекера-Капелли

Матрица, получающаяся конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ $$ [ A| ] = left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ $$ называется расширенной матрицей системы линейных уравнений $ AX= $.

Теорема [Кронекер, Капелли]. Система $ AX= $ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

$$ operatorname, A = operatorname, [ A| ] . $$ При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_ $ совпадает с общим значением ранга $ mathfrak r_ $, и бесконечное множество решений, если $ n_ $ больше этого значения.

Доказательство необходимости. Пусть существует решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы, тогда $$alpha_1 A_+dots+alpha_n A_= ,$$ т.е. столбец $ $ линейно выражается через столбцы $ A_,dots,A_ $. Но тогда $$ operatorname <A_,dots,A_>=operatorname <A_,dots,A_,> .$$ Следовательно $ operatorname, A = operatorname, [ A| ] $.

Доказательство достаточности проводится в следующем пункте. ♦

Пример. Исследовать совместность системы уравнений

Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы $ det A_ $. Если он отличен от нуля — система совместна. $$det A = left| begin<color> &1&1&1 \ 1&<color>&1&1 \ 1&1&<color>&1 \ 1&1&1&<color> end right|= left| begin (<color>-1) &(1-<color>)&0&0 \ 0&(<color>-1)&(1-<color>)&0 \ 0&0&(<color>-1)&(1-<color>) \ 1&1&1&<color> end right| =(<color>-1)^3 left| begin 1 &-1&0&0 \ 0&1&-1&0 \ 0&0&1&-1 \ 1&1&1&<color> end right|= $$ $ =(<color>-1)^3(<color>+3) $. По теореме Крамера при $ <color>ne 1 $ и при $ <color>ne -3 $ решение системы единственно: $$x_1=x_2=x_3=x_4=1/(<color>+3) .$$

Осталось исследовать критические случаи: $ <color>=1_ $ и $ <color>= -3 $: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При $ <color>= 1_ $ имеем $$ operatorname left( begin 1 &1&1&1 \ 1&1&1&1 \ 1&1&1&1 \ 1&1&1&1 end right)= operatorname left( begin 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 end right)=1 , $$ и система совместна. Она эквивалентна единственному уравнению $$x_1+x_2+x_3+x_4=1 ,$$ которое имеет бесконечно много решений.

При $ <color>= -3 $: $$ operatorname left( begin -3 &1&1&1 \ 1&-3&1&1 \ 1&1&-3&1 \ 1&1&1&-3 end right)=3,quad operatorname left( begin -3 &1&1&1&1 \ 1&-3&1&1&1 \ 1&1&-3&1&1 \ 1&1&1&-3&1 end right)=4 $$ и система несовместна.

Ответ. Система несовместна при $ <color> = -3 $; она имеет бесконечное множество решений при $ <color> = 1_ $ и единственное решение при $ <color> notin $.

Система однородных уравнений

$$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0 end right. $$ всегда совместна: она имеет тривиальное решение $ x_1=0,dots,x_n=0 $. Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_) $ лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_ $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений: $$ left< begin ax_1+by_1+c & =0\ ax_2+by_2+c & =0\ ax_3+by_3+c & =0 end right. $$ Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора $ (a,b,c)_ $ при хотя бы одном из чисел отличном от нуля): $$ left|begin x_1 & y_1 & 1 \ x_2 & y_2 & 1 \ x_3 & y_3 & 1 end right|=0 . $$ ♦

Доказать, что для совместности системы

$$ left< begin a_x_1+a_x_2+a_x_3 &=& b_1 \ a_x_1+a_x_2+a_x_3 &=& b_2 \ a_x_1+a_x_2+a_x_3 &=& b_3 \ a_x_1+a_x_2+a_x_3 &=& b_4 end right. $$ необходимо, чтобы было выполнено условие $$ left| begin a_&a_& a_ & b_1 \ a_&a_& a_ & b_2 \ a_&a_& a_ & b_3 \ a_&a_& a_ & b_4 end right|=0 quad . $$ Является ли это условие достаточным для совместности?

An elementary treatise on determinants

в следующей формулировке.

Теорема. Для того чтобы система $ n_ $ неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.

Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.

Ответ ☞ ЗДЕСЬ

Видео:Теорема о структуре общего решения однородной системы линейных уравненийСкачать

Общее решение

Пусть выполнено условие теоремы Кронекера-Капелли: $ operatorname (A)=operatorname[Amid mathcal B ] =mathfrak $. По определению ранга матрицы, в матрице $ A $ существует минор порядка $ mathfrak $, отличный от нуля; этот же минор останется и минором расширенной матрицы $ [ Amid mathcal B ] $. Пусть, для определенности, ненулевой минор находится в левом верхнем углу матрицы 4) : $$ Delta = Aleft( begin 1 & 2 & dots & mathfrak \ 1 & 2 & dots & mathfrak end right) = left| begin a_ & a_ & dots & a_<1mathfrak> \ a_ & a_ & dots & a_<2mathfrak> \ dots &&& dots \ a_<mathfrak1> & a_<mathfrak2> & dots & a_ <mathfrakmathfrak> end right| ne 0 . $$ Тогда первые $ mathfrak $ строк матрицы $ A $ линейно независимы, а остальные будут линейно выражаться через них. Это же утверждение будет справедливо и для строк матрицы $ [Amid mathcal B] $. Умножая первые $ mathfrak $ уравнений системы на соответствующие числа и складывая их, получим любое оставшееся уравнение. Таким образом, система уравнений может быть заменена эквивалентной ей системой из первых $ mathfrak $ уравнений: $$ left< begin a_x_1+dots+a_<1mathfrak>x_<mathfrak>&+a_<1,mathfrak+1>x_<mathfrak+1>+ dots +a_x_n&=&b_1, \ dots & & & dots \ a_<mathfrak1>x_1+dots+a_<mathfrakmathfrak>x_<mathfrak>& +a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n&=&b_mathfrak end right. quad iff quad A^ X=^ $$ Если $ mathfrak=n $, то матрица $ A^ $ квадратная. По предположению $ det A^ ne 0 $. По теореме Крамера решение такой системы единственно.

Пусть теперь $ mathfrak произвольных фиксированных значениях $ x_<mathfrak+1>,dots,x_n $: $$ x_j=frac< left| begin a_ & dots &a_ &left[ b_1-(a_<1,mathfrak+1>x_<mathfrak+1>+dots +a_x_n) right] &a_& dots &a_<1mathfrak> \ dots &&&dots&&& dots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & left[ b_<mathfrak>- (a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n) right] &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| > $$ $$ mbox jin <1,dots, mathfrak> . $$ Таким образом, в этом случае система имеет бесконечное множество решений. Используя свойство линейности определителя по столбцу (см. свойство 5 ☞ ЗДЕСЬ ), формулы можно переписать в виде $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Здесь $$ beta_j =frac left| begin a_ & dots &a_ & b_1 &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & b_<mathfrak> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right|, , $$ $$ gamma_ = -frac left| begin a_ & dots &a_ & a_ &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & a_<mathfrakk> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| . $$ Эти формулы называются общим решением системы $ A X=mathcal B $. Участвующие в них переменные $ x_<mathfrak+1>,dots,x_n $ называются основными (или свободными), а $ x_1,dots,x_<mathfrak> $ — зависимыми. Решение, получающееся из общего решения фиксированием значений основных переменных, называется частным решением системы уравнений.

Пример. Исследовать совместность и найти общее решение системы уравнений:

Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров: $$ |2| ne 0,quad left| begin 2 & 1 \ 6 & 2 end right| ne 0, quad left| begin 2 & 1 & 2 \ 6 & 2 & 4 \ 4 & 1 & 1 end right|=2 ne 0 , $$ а все миноры, окаймляющие последний, равны нулю. Итак, $ operatorname (A) =3 $. Для нахождения ранга расширенной матрицы $ [Amid mathcal B] $ достаточно проверить окаймление найденного ненулевого минора третьего порядка с помощью элементов взятых из столбца правых частей. Имеется всего один такой минор, и он равен нулю. Следовательно $ operatorname[ Amid mathcal B ] =3 $, система совместна, и имеет бесконечное множество решений.

Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках, что означает линейную независимость соответствующих уравнений. Третье уравнение линейно зависит от остальных, и может быть отброшено. Далее, указанный базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $. Следовательно оставшиеся уравнения могут быть разрешены относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ — основные. Использование формулы дает общее решение $$ begin x_1&=&frac<left| begin 2 & 1 & 2 \ 3 & 2 & 4 \ 1 & 1 & 1 end right|> -x_2frac<left| begin -1 & 1 & 2 \ -3 & 2 & 4 \ -2 & 1 & 1 end right|> -x_5frac<left| begin 3 & 1 & 2 \ 5 & 2 & 4 \ 2 & 1 & 1 end right|> =-frac+fracx_2+fracx_5, \ & & \ x_3&=&frac<left| begin 2 & 2 & 2 \ 6 & 3 & 4 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & -1 & 2 \ 6 & -3 & 4 \ 4 & -2 & 1 end right|> -x_5frac<left| begin 2 & 3 & 2 \ 6 & 5 & 4 \ 4 & 2 & 1 end right|>=3-4x_5, \ & & \ x_4 &=&frac<left| begin 2 & 1 & 2 \ 6 & 2 & 3 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & 1 & -1 \ 6 & 2 & -3 \ 4 & 1 & -2 end right|> -x_5frac<left| begin 2 & 1 & 3 \ 6 & 2 & 5 \ 4 & 1 & 2 end right|> = 0. end $$ Решим теперь ту же задачу, воспользовавшись методом Гаусса исключения переменных в системе линейных уравнений: $$ left< begin 2x_1&-x_2&+x_3&+2x_4&+3x_5&=&2, \ &&x_3&+2x_4&+4x_5&=&3, \ &&&x_4&&=&0 end right. $$ Используя обратный ход метода Гаусса, снова приходим к полученным формулам.

Ответ. Общее решение системы: $ x_1=1/2 (x_2+x_5-1), x_3=3-4,x_5, x_4=0 $.

Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ beta_j $ представляет решение системы, получаемое при $ x_<mathfrak+1>=0,dots,x_n=0 $. Величины же коэффициентов $ gamma_ $ вовсе не зависят от правых частей системы и будут одинаковыми при любых значениях $ b_1,dots,b_m $. В частности, если $ b_1=0,dots,b_m=0 $, то в формулах величины $ beta_j $ обращаются в нуль и эти формулы превращаются в $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$

Вывод. Формула общего решения системы $ A X=mathcal B $: $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> $$ состоит из двух частей: слагаемые, не содержащие свободных переменных, определяют частное решение неоднородной системы: $$ x_1= beta_1,dots, x_<mathfrak>= beta_<mathfrak>,x_<mathfrak+1>=0,dots,x_n=0 ; $$ оставшиеся после их отбрасывания формулы задают общее решение системы $ AX=mathbb O $. Этот результат обобщается в следующей теореме.

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Доказательство тривиально если система $ A X=mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением $$ A(X_2-X_1)=mathbb O , $$ т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=mathbb O $. ♦

Теперь посмотрим как можно описать общее решение однородной системы.

Система однородных уравнений

Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0. end right. $$ или, в матричном виде: $$ A_X=_ $$

Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрица $ A_ $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие $ det (A_) = 0 $ является и достаточным для существования нетривиального решения.

Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_ $ имела нетривиальное решение необходимо и достаточно, чтобы $ det (A_) = 0 $.

Для произвольной (не обязательно квадратной) матрицы $ A_ $ имеет место следующий общий результат.

Теорема 2. Если $ operatorname (A)=mathfrak r 5) $ A_^ $.

Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ mathbb A^ $. Размерность этого подпространства равна $ n-mathfrak r $, а фундаментальная система решений образует его базис.

Пусть матрица системы $ AX=mathbb O $ квадратная и

$$ operatorname (A) =n_-1 , .$$ Доказать, что если ненулевой минор матрицы порядка $ n_-1 $ соответствует какому-нибудь элементу $ j_ $-й строки, то система алгебраических дополнений к элементам $ a_,dots,a_^ $ этой строки составляет ФСР для $ AX=mathbb O_ $. Например, для системы $$ left< begin a_x_1 +a_x_2+a_x_3&=0,\ a_x_1 +a_x_2+a_x_3&=0 end right. $$ ФСР состоит из решения $$ x_1=left| begin a_ & a_ \ a_ & a_ end right| , x_2=-left| begin a_ & a_ \ a_ & a_ end right| , x_3=left| begin a_ & a_ \ a_ & a_ end right| , $$ если только хотя бы один из миноров отличен от нуля.

Теперь обсудим способы нахождения ФСР.

1. Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_,dots,x_ $, т.е. общее решение задается формулами $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Иными словами, вектор столбец $$ X=left(begin gamma_<1,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ gamma_<2,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ vdots \ gamma_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots+gamma_<mathfrakn>x_n \ x_<mathfrak+1> \ x_<mathfrak+2> \ vdots \ x_ endright) $$ будет решением однородной системы при любых наборах значений основных переменных $ x_<mathfrak+1>,dots,x_ $. Представим этот вектор в виде суммы векторов: $$ =x_<mathfrak+1> underbrace< left(begin gamma_<1,mathfrak+1> \ gamma_<2,mathfrak+1> \ vdots \ gamma_<mathfrak,mathfrak+1> \ 1 \ 0 \ vdots \ 0 endright)>_ + x_<mathfrak+2> underbrace<left(begin gamma_<1,mathfrak+2> \ gamma_<2,mathfrak+2> \ vdots \ gamma_<mathfrak,mathfrak+2> \ 0 \ 1 \ vdots \ 0 endright)>_+dots+ x_ underbrace<left(begin gamma_ \ gamma_ \ vdots \ gamma_<mathfrakn> \ 0 \ 0 \ vdots \ 1 endright)>_<X_> . $$ Таким образом, любое решение однородной системы представимо в виде линейной комбинации $ n_- mathfrak r $ фиксированных решений. Именно эти решения и можно взять в качестве ФСР — их линейная независимость очевидна (единицы в нижних частях каждого вектора $ X_ $ расположены на разных местах, и ни какая линейная комбинация столбцов $ < X_1,dots,X_> $ не сможет обратить их одновременно в нуль).

Оформим этот способ построения ФСР в теорему:

Теорема 4. Если система уравнений $ AX=mathbb O $ имеет структуру матрицы $ A_ $ вида:

$$ A = left[ E_ mid P_ right] , $$ то ее ФСР состоит из столбцов матрицы $$ left[ begin — P^ \ hline E_ end right] . $$

Пример. Найти ФСР для системы уравнений

Решение. Приводим систему к трапециевидному виду: $$ left< begin x_1-&x_2+&x_3-&x_4=&0, \ &&x_3+&4x_4=&0 end right. $$ В качестве зависимых переменных можно взять, например, $ x_ $ и $ x_ $. $$ begin x_1 & x_3 & x_2 & x_4 \ hline 1 & 0 & 1 & 0 \ 5 & -4 & 0 & 1 end $$

2. Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_ $ системы и припишем к ней справа единичную матрицу порядка $ n_ $: $$ left[ A^ | E_n right] = left(begin a_ & a_ & dots & a_ & 1 & 0 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 1 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 0 & 1 & dots & 0 \ vdots & & & vdots & vdots & & & ddots & vdots \ a_ & a_ & dots & a_ & 0 & 0 & 0 & dots & 1 end right) ; $$ здесь $ |_ $ означает конкатенацию. Получившуюся матрицу элементарными преобразованиями строк приводим к форме: $$ left( begin hat A & K \ mathbb O & L end right) = left(begin color & * & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & color & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & 0 & color & dots & * & * & * & * & * & * & * & dots & * \ vdots & & & ddots & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & & 0 & color & * & * & * & * & * & dots & * \ hline 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box \ vdots & & & & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box end right) begin left.begin \ \ \ \ \ endright> mathfrak r \ left. begin \ \ \ endright> n — mathfrak r end . $$ Элементы трапециевидной матрицы $ hat A $, обозначенные $ color $, могут быть равны нулю, но $ operatorname(hat A)= mathfrak r_ $. В этом случае строки матрицы $ L_ $, образовавшейся в правом нижнем углу (ее элементы обозначены $ Box $), составляют ФСР для системы $ AX=mathbb O $.

Пример. Найти ФСР для системы уравнений

$$ left< begin x_1 &+2,x_2&+ x_3&+3,x_4&-x_5&+2,x_6=&0,\ -3x_1 &-x_2&+ 2,x_3&-4,x_4&+x_5&-x_6=&0,\ x_1 &+x_2&+ 3,x_3&+2,x_4&+x_5&+3,x_6=&0,\ -8,x_1 &-7,x_2&+ 4,x_3&-15,x_4&+6,x_5&-5,x_6=&0,\ 6x_1 &+5,x_2& +5,x_3&+11,x_4 &&+9,x_6=&0. end right. $$ Решение. Преобразуем матрицу $ left[ A^ | E_6 right] $

$$ left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 2 & -1 & 1 & -7 & 5 & & 1 \ 1 & 2 & 3 & 4 & 5 & & & 1 \ 3 & -4 & 2 & -15 & 11 &&&& 1 \ -1 & 1 & 1 & 6 & 0 &&&&& 1 \ 2 & -1 & 3 & -5 & 9 &&&&&& 1 end right)_ $$ к трапециевидной форме с помощью элементарных преобразований строк: $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 5 & 2 & 12 & -1 &-1 &0 & 1 \ 0 & 5 & -1 & 9 & -7 &-3&0&0& 1 \ 0 & -2 & 2 & -2 & 6 &1&0&0&0& 1 \ 0 & 5 & 1 & 11 & -3 &-2&0&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 8/5 & 8/5 & 16/5 &1/5&2/5&0&0& 1 \ 0 & 0 & 2 & 2 & 4 &0&-1&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 0 & 0 & 0 &-1/3&14/15&-8/15&0& 1 \ 0 & 0 & 0 & 0 & 0 &-2/3&-1/3&-2/3&0& 0 & 1 end right) $$

3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.

Теорема. Пусть матрица системы $ AX=mathbb O $ квадратная и $ operatorname (A) = $. Тогда характеристический полином матрицы $ A_ $ имеет вид:

Пример. Найти ФСР для системы уравнений

Решение. Здесь $$ A= left( begin 1 & 1 & -1 & -1 \ 2 & 3 & 1 & -2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right), quad det (A-lambda E) = lambda^2(lambda^2-4lambda+1), $$ $$ A^2-4A+E= left( begin 0 & 0 & 4 & 1 \ 0 & 0 & -3 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 end right) $$

Блок-схемы зависимости множества решений системы уравнений $ AX= mathcal B $ от комбинации чисел $ n, mathfrak r $ ☞ ЗДЕСЬ.

Видео:Неоднородная система линейных уравненийСкачать

Геометрическая интерпретация

Геометрический смысл введенных определений поясним на примере $ mathbb R^ $. Уравнение $$ a_1x_1+a_2x_2+a_3x_3=b $$ — при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_ $ — задает плоскость. Если, к примеру, $ a_1ne 0 $, то из уравнения получаем выражение для $ x_ $ как функции $ x_2,x_3 $: $$ x_1=frac-fracx_2-fracx_3 . $$ В этом представлении переменные $ x_ $ и $ x_ $ могут принимать любые вещественные значения независимо друг от друга, а вот переменная $ x_ $ полностью определяется заданием $ x_ $ и $ x_ $. С одной стороны, последняя формула определяет общее решения системы линейных уравнений (которая в нашем частном случае состоит из одного-единственного уравнения); переменные $ x_ $ и $ x_ $ выбраны основными, а $ x_ $ оказывается зависимой. Строго говоря, координаты любой точки плоскости можно представить формулами $$x_1=frac-fract-fracu, x_2=t, x_3=u quad npu quad subset mathbb R , $$ которые называются параметрическим представлением плоскости. Таким образом, получили геометрическую интерпретацию общего решения системы уравнений. Идем далее: представим последние формулы в векторной форме: $$ left( begin x_1 \ x_2 \ x_3 end right)= left( begin b/a_1- t, a_2/a_1- u, a_3/a_1 \ t \ u end right)= left( begin b/a_1\ 0 \ 0 end right)+ t left( begin -a_2/a_1\ 1 \ 0 end right) + u left( begin -a_3/a_1\ 0 \ 1 end right) . $$ Какой геометрический смысл имеет каждое из слагаемых? Первое слагаемое $$ X_0=left( begin b/a_1\ 0 \ 0 end right) $$ получается при задании $ t=0,u=0_ $ в общем решении. Это — частное решение нашего уравнения и определяет точку, через которую проходит плоскость. Два оставшихся столбца $$ X_1=left( begin -a_2/a_1\ 1 \ 0 end right) quad u quad X_2=left( begin -a_3/a_1\ 0 \ 1 end right) $$ не задают решения нашего уравнения — если только $ bne 0_ $. Но оба удовлетворяют однородному уравнению $$ a_1x_1+a_2x_2+a_3x_3=0 , $$ Последнее также определяет плоскость — параллельную исходной и проходящую через начало координат. Первая плоскость получается из второй сдвигом (параллельным переносом) на вектор $ vec $: и этот факт составляет геометрическую интерпретацию теоремы, сформулированной в конце ☞ ПУНКТА:

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Координаты произвольной точки плоскости $ a_1x_1+a_2x_2+a_3x_3=0 $ задаются соотношениями $$ left( begin x_1 \ x_2 \ x_3 end right)=tX_1+uX_2 . $$ Векторы пространства $ vec $ и $ vec $ являются базисными векторами плоскости — любой вектор $ vec $, лежащий в плоскости, через них выражается и они линейно независимы. Но $ X_ $ и $ X_ $ определяют фундаментальную систему решений однородного уравнения. Таким образом, мы получили геометрическую интерпретацию для ФСР: она задает базисные векторы плоскости, проходящей через начало координат.

Теперь рассмотрим систему из двух уравнений: $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2. endright. $$ Ее можно интерпретировать как пересечение двух плоскостей в $ mathbb R^ $. Здесь уже возможны варианты: пересечение может оказаться как пустым так и непустым. От чего это зависит? — В соответствии с теоремой Кронекера-Капелли, надо сравнить два числа $$ operatorname left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) quad u quad operatorname left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) . $$ Очевидно, ни одно из них не может быть большим $ 2_ $. Если оба равны $ 2_ $ и этот факт обеспечен, например, условием $$ left| begin a_ & a_ \ a_ & a_ end right| ne 0, $$ то решения системы определяют прямую в пространстве. Действительно, при таком условии систему можно разрешить относительно неизвестных $ x_ $ и $ x_ $ и представить общее решение в виде: $$ x_1= frac<left|begin b_1 & a_ \ b_2 & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>+ frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 , quad x_2= frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>- frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 . $$ В этих формулах переменная $ x_ $ принимает любое значение, а значения переменных $ x_ $ и $ x_ $ линейно выражаются через $ x_ $. Общее решение фактически задает прямую в параметрическом виде: координаты произвольной ее точки определяются формулами $$ left( begin x_1 \ x_2 \ x_3 end right)=X_0+tX_1 , $$ где вектор $$ quad X_0 = left(frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|> , frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 0right)^ $$ задает координаты точки, лежащей на прямой (т.е. принадлежащей пересечению плоскостей), а вектор $$ X_1= left(frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, — frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 1 right)^ $$ является направляющим для прямой. С тем же успехом мы могли бы взять в качестве направляющего вектор, получающийся растяжением $ X_ $: $$ tilde X_1 = left(left|begin a_ & a_ \ a_ & a_ end right|, — left|begin a_ & a_ \ a_ & a_ end right|, left|begin a_ & a_ \ a_ & a_ end right| right)^ . $$ Очевидно, что любой из векторов $ X_ $ или $ tilde X_1 $ задает фундаментальную систему решений однородной системы уравнений 10) $$ left<begin a_x_1 +a_x_2+a_x_3 &=&0,\ a_x_1 +a_x_2+a_x_3 &=&0. endright. $$ Последняя определяет прямую в $ mathbb R^3 $, проходящую через начало координат. Мы снова получаем интерпретацию теоремы: общее решение неоднородной системы получается сдвигом (параллельным переносом) общего решения однородной системы на вектор $ vec $.

Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ mathbb R^ $ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы $$ left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) $$ оказался меньшим $ 2_ $. Это равносильно тому, что все миноры второго порядка этой матрицы обращаются в нуль: $$ left| begin a_ & a_ \ a_ & a_ end right|=0, left| begin a_ & a_ \ a_ & a_ end right| =0, left| begin a_ & a_ \ a_ & a_ end right|=0 . $$ Эти условия можно переписать в виде $$ frac<a_><a_>=frac<a_><a_>=frac<a_><a_> ; $$ и, если обозначить общую величину последний отношений через $ tau_ $, то получаем: $$ (a_,a_,a_)=tau (a_,a_,a_) . $$ Если вспомнить, что каждый из этих наборов коэффициентов задает вектор $ vec<OA^> $ в $ mathbb R^ $, перпендикулярный соответствующей плоскости, то, в самом деле, плоскости, определяемые уравнениями, оказываются параллельными. Пересекаться они, как правило, не будут: для пересечения необходимо, чтобы расширенная матрица системы $$ left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) $$ имела ранг меньший $ 2_ $. Это возможно только при условии когда коэффициенты правых частей удовлетворяют соотношению $$ b_1 = tau b_2 $$ при величине $ tau_ $ определенной выше. При выполнении этого условия второе уравнение получается из первого домножением на $ tau_ $ и соответствующие плоскости попросту совпадают.

Перейдем теперь к системе из трех уравнений: $$ left< begin a_x_1 +&a_x_2+&a_x_3=&b_1, \ a_x_1 +&a_x_2+&a_x_3=&b_2, \ a_x_1 +&a_x_2+&a_x_3=&b_3. end right. $$ Вариантов взаимного расположения трех плоскостей в $ mathbb R^ $ уже значительно больше. Какой из них будет самым распространенным, то есть случаем «как правило»? Геометрически ответ очевиден: если пересечение двух плоскостей определяет, как правило, прямую, то эта прямая пересекается с третьей плоскостью, как правило, в одной-единственной точке. И алгебра подтверждает геометрию: в комментарии к теореме Крамера говорится, что система, число уравнений которой совпадает с числом неизвестных, как правило, имеет единственное решение. Условие для этого случая «как правило» дается той же теоремой Крамера: $$ left| begin a_ & a_ & a_\ a_ & a_ & a_ \ a_ & a_ & a_ end right| ne 0 . $$

Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_ $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_,a_, a_) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2 endright. $$ определяет прямую в $ mathbb R^ $, то оба вектора $ vec<OA^> $ и $ vec<OA^> $ при $ A^= (a_,a_, a_) $ и $ A^= (a_,a_, a_) $ перпендикулярны этой прямой; любая их комбинация также перпендикулярна этой прямой, а, следовательно, плоскость $$ a_x_1 +a_x_2+a_x_3 =b_3 $$ будет ей параллельна.

Статья не закончена!

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Ортогональность

Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.

Задача решения системы линейных уравнений $$ left< begin 3x_1&+4x_2&-x_3&=2, \ x_1&-2x_2&+3x_3&=1 end right. $$ может быть рассмотрена с двух точек зрения. С одной стороны, переписав систему в виде $$ x_1left(begin 3 \ 1 end right)+ x_2left(begin 4 \ -2 end right)+ x_3left(begin -1 \ 3 end right)= left(begin 2 \ 1 end right) , $$ можно говорить о поиске линейной комбинации столбцов $$ left(begin 3 \ 1 end right), left(begin 4 \ -2 end right), left(begin -1 \ 3 end right) $$ равной заданному столбцу $$ left(begin 2 \ 1 end right) . $$ В случае произвольной системы, записанной в матричном виде $$ A_X=mathcal B_ $$ совместность системы интерпретировать в смысле принадлежности столбца $ mathcal B $ линейной оболочке столбцов $ A_,dots,A_ $: $$ mathcal B=x_1 A_+dots+x_nA_ quad iff quad mathcal B in mathcal L (A_,dots,A_) . $$ В случае положительного ответа числа $ x_,dots,x_n $ интерпретируются как координаты столбца $ mathcal B $ в системе столбцов 11) $ <A_,dots,A_> $.

С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы $$ 3,x_1+4,x_2-x_3=2 $$ можно интерпретировать так: скалярное произведение векторов $ vec<^> $ и $ vec<> $ равно фиксированному числу $ 2_ $. Здесь вектора рассматриваются в пространстве строк $ mathbb R_^ $; считается, что каждый вектор имеет начало в начале координат $ mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ langle mbox rangle $, то систему уравнений можно переписать в виде $$ langle vec<^> , vec<> rangle=2, langle vec<^> , vec<> rangle=1 quad npu quad A^ = [3,4,-1], A^=[1,-2,3] $$ — строках матрицы $ A_ $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.

Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений $$ left< begin 3x_1&+4x_2&-x_3&=0, \ x_1&-2x_2&+3x_3&=0 end right. $$ означает подобрать вектор $ vec<> $ перпендикулярный (ортогональный) одновременно обоим векторам $ vec<^> $ и $ vec<^> $. Очевидно, что таких векторов в $ mathbb R^ $ бесконечно много — найдя хотя бы один такой вектор $ vec<> $, другие получим его растяжением: $ alpha cdot vec<> $ остается перпендикулярным векторам $ vec<^> $ и $ vec<^> $ при $ forall alpha in mathbb R $.

Все эти геометрические соображения обобщаются в произвольное пространство $ mathbb R_^ $ строк или столбцов, состоящих из $ n_ $ вещественных чисел (компонент). Для этого приходится обобщать понятие скалярного произведения. В общем случае оно вводится аксиоматически (и, более того, в одном и том же множестве может быть определено разными способами, см. ☞ ЕВКЛИДОВО ПРОСТРАНСТВО ). Мы сейчас не будем залезать так глубоко в эту аксиоматику, а просто определим скалярное произведение двух строк $ X=[x_1,x_2,dots,x_n] $ и $ Y=[y_1,y_2,dots,y_n] $ формулой $$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n $$ и продекларируем без обоснований, что все привычные нам по случаям $ mathbb R^ $ и $ mathbb R^ $ свойства скалярного произведения будут выполнены.

В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,dots,x_n] $, ортогональной всем строкам матрицы $ A_ $: $$ langle A^,X rangle=0, langle A^,X rangle=0,dots, langle A^,X rangle=0 . $$ Множество таких строк образует линейное подпространство пространства $ mathbb R_^ $, это подпространство является ортогональным дополнением линейной оболочки $ mathcal L ( A^, A^,dots, A^ ) $ в пространстве $ mathbb R_^ $. Это подпространство называется нуль-пространством матрицы или ядром матрицы $ A_ $ и обозначается 12) $ er (A) $. Фундаментальная система решений системы $ AX=mathbb O $ составляет базис этого подпространства. Для произвольного линейного пространства количество векторов его базиса называется размерностью пространства и обозначается $ operatorname $. Во введенных обозначениях теорема из ☞ ПУНКТА переформулируется так:

Теорема. $ operatorname left( er (A) right)=n- mathfrak r $, где $ n_ $ — количество столбцов матрицы $ A_ $, а $ mathfrak r=operatorname (A) $ — ее ранг.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Видео:Существование и единственность Теорема и задачи ДзСкачать

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

🔍 Видео

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать