Теорема о пространстве решений системы линейных уравнений

Пусть дана система (30) линейных однородных уравнений с коэффициентами из поля Р.

(30)

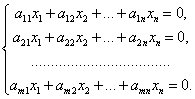
Так как столбец свободных членов в матрице А1 этой системы состоит только из нулей, то rang A = rang A1, т. е. система линейных однородных уравнений всегда совместна. В частности она всегда имеет нулевое решение. Рассмотрим множество всех возможных решений системы (30).

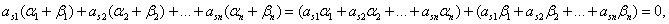
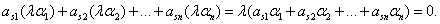
Пусть A =(A1, A2, … , An) и B =(B1, B2, … , Bn) – Любые два из них. Их можно рассматривать, как векторы в арифметическом n-мерном пространстве над полем Р. Пусть L – любой элемент поля Р. Тогда A +B = (A1 + B1, A2 + B2, … , An + Bn ), L×A = (LA1, LA2, … , LAn). Подставим компоненты этих векторов в произвольное S-е уравнение системы (30). Получим Итак, если A и B – Любые два решения системы (30) и L – любой элемент поля Р, то A +B И L×A тоже являются решением этой системы. Но тогда из теоремы 14 следует

Теорема 27. Множество решений системы линейных однородных уравнений с N Переменными есть линейное подпространство арифметического пространства Аn .

Теорема 28. Размерность пространства решений системы линейных однородных уравнений равна N – r, Где N – Число неизвестных, r – ранг матрицы системы.

Доказательство. Пусть L – пространство решений системы (30). Тогда L Ì Аn . Пусть A = (A1, A2, … Ar, Ar+1, … , An) – произвольное решение системы. Пусть (Ar+1, … , An) – набор свободных неизвестных, соответствующий этому решению. Множество всех возможных наборов свободных неизвестных есть арифметическое (N – r)-мерное пространство Аn–r . Зададим отображение J: L ® Аn–r по правилу

Покажем, что J – изоморфизм (определение 24). Для этого нужно проверить три условия.

1. Покажем, что J – взаимнооднозначное отображение. Решению A = (A1, A2, … Ar, Ar+1, … , An) соответствует только один набор (Ar+1, … , An), следовательно, J – Однозначное отображение. Обратно, если задать элемент (Ar+1, … , An) из Аn–r , то по теореме Крамера найдётся только один набор (A1, A2, … Ar ) искомых неизвестных, т. е. каждый элемент J(A) из Аn–r соответствует единственному элементу из L .

Итак, пространство решений системы линейных однородных уравнений изоморфно арифметическому (N – r)-мерному пространству. Следовательно, размерность L равна (N – r).

Определение 29. Базис пространства решений системы линейных однородных уравнений называется её Фундаментальной системой решений.

Так как при изоморфизме базис пространства Аn–r соответствует базису пространства L , То для того. чтобы найти фундаментальную систему решений для системы (30), достаточно выбрать (N – r) линейно независимых наборов свободных неизвестных и для каждого из них найти решение данной системы.

Следствие. Если А1, а2, …, аN–r фундаментальная система решений системы линейных однородных уравнений (30) и С1, С2, … , СN–r – произвольные элементы поля Р, то С1А1 + С2А2 + … + СN–r АN–r – общее решение этой системы.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Общая теория систем линейных уравнений

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Условия совместности.

Займемся изучением систем из m уравнений с n неизвестными. Систему
begina_^x^+a_^x^+. +a_^x^=b^,\a_^x^+a_^x^+. +a_^x^=b^,\cdots\a_^x^+a_^x^+. +a_^x^=b^end мы можем кратко записать в виде tag Aboldsymbol=boldsymbol.
Система задается своей расширенной матрицей A^ , получаемой объединением матрицы системы A и столбца свободных членов boldsymbol .

Простое и эффективное условие, необходимое и достаточное для совместности системы (1) , дает следующая теорема, называемая теоремой Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров m times n столбца boldsymbol высоты m не меняет ее ранга тогда и только тогда, когда этот столбец — линейная комбинация столбцов A .

Если mathbf,A^ = mathbf,A , то базисный минор A является базисным и для A^ . Следовательно, boldsymbol раскладывается по базисным столбцам A . Мы можем считать его линейной комбинацией всех столбцов A , добавив недостающие столбцы с нулевыми коэффициентами.

Обратно, если boldsymbol раскладывается по столбцам A , то элементарными преобразованиями столбцов можно превратить A^ в матрицу A_ , получаемую из A приписыванием нулевого столбца. Из утверждения о том, что ранг матрицы не меняется при элементарных преобразованиях, следует mathbf,A_ = mathbf,A^ . С другой стороны, mathbf,A_ = mathbf,A , так как добавление нулевого столбца не может создать новых невырожденных подматриц. Отсюда mathbf,A = mathbf,A^ , как и требовалось.

Иначе это утверждение можно сформулировать так.

Система линейных уравнений несовместна тогда и только тогда, когда противоречивое равенство 0=1 является линейной комбинацией ее уравнений.

Равенство рангов матрицы системы и расширенной матрицы можно выразить, понимая ранг матрицы как строчный ранг. Это приведет нас к важной теореме, известной как теорема Фредгольма.

Транспонируем матрицу A системы (1) и рассмотрим систему из n линейных уравнений tag begin a_^y_+a_^y_+. +a_^y_=0,\ a_^y_+a_^y_+. +a_^y_=0,\cdots\a_^y_+a_^y_+. +a_^y_=0end с m неизвестными, матрицей A^ и свободными членами, равными нулю. Она называется сопряженной однородной системой для системы (1) . Если boldsymbol — столбец высоты m из неизвестных, то систему (2) можно записать как A^ boldsymbol=boldsymbol , или лучше в виде tag boldsymbol^A=boldsymbol, где boldsymbol — нулевая строка длины n .

Для того чтобы система (1) была совместна, необходимо и достаточно, чтобы каждое решение сопряженной однородной системы (3) удовлетворяло уравнению tag boldsymbol^ boldsymbol=y_b^+. +y_b^=0.

1^ . Пусть система (1) совместна, то есть существует столбец boldsymbol высоты n , для которого Aboldsymbol=boldsymbol . Тогда для любого столбца boldsymbol высоты m выполнено boldsymbol^ Aboldsymbol=boldsymbol^ boldsymbol . Если boldsymbol — решение системы (3) , то boldsymbol^ boldsymbol=(boldsymbol^ A)boldsymbol=boldsymbolboldsymbol=0 .

2^ . Предположим теперь, что система (1) несовместна. Тогда согласно утверждению 1 строка begin 0&. & 0& 1 end входит в упрощенный вид расширенной матрицы A^=begin A& |& boldsymbol end и, следовательно, является линейной комбинацией ее строк. Обозначим коэффициенты этой линейной комбинации y_. y_ и составим из них столбец boldsymbol . Для этого столбца boldsymbol^ begin A& |& boldsymbol end=begin 0&. & 1 end (согласно данного утверждения). Это же равенство можно расписать как два: boldsymbol^ A=boldsymbol и boldsymbol^ boldsymbol=1 . Итак, нам удалось найти решение системы (3) , не удовлетворяющее условию (4) . Это заканчивает доказательство.

В качестве примера применим теорему Фредгольма к выводу условия параллельности двух различных прямых на плоскости. Их уравнения составляют систему A_x+B_y+C_=0, A_x+B_y+C_=0.
Она не имеет решений, если существуют такие числа y_, y_ , что y_A_+y_A_=0 , y_B_+y_B_=0 , но y_C_+y_C_ neq 0 . Ясно, что y_ и y_ не равны нулю. Поэтому можно положить lambda=-y_/y_ и записать полученное условие в виде: существует число lambda такое, что A_=lambda A_ , B_=lambda B_ и C_ neq lambda C_ .

Видео:Решение системы уравнений методом ГауссаСкачать

Нахождение решений.

В этом пункте мы будем предполагать, что дана совместная система из m линейных уравнений с n неизвестными. Ранг матрицы системы обозначим r . Поскольку ранг расширенной матрицы тоже равен r , мы можем считать базисные столбцы матрицы системы базисными столбцами расширенной матрицы. Элементарными преобразованиями строк приведем расширенную матрицу к упрощенному виду (возможность этого мы уже доказывали). Наша система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений.

Для удобства записи будем предполагать, что первые r столбцов — базисные. Тогда преобразованную систему можно записать в виде tag begin x^=beta^-(alpha_^x^+. +alpha_^x^),\cdots\x^=beta^-(alpha_^x^+. +alpha_^x^).end
Здесь alpha_^ и beta^ — элементы преобразованной расширенной матрицы. В левых частях равенств мы оставили неизвестные, соответствующие выбранным нами базисным столбцам, так называемые базисные неизвестные. Остальные неизвестные, называемые параметрическими, перенесены в правые части равенств.

Как бы мы ни задали значения параметрических неизвестных, по формулам (5) мы найдем значения базисных так, что они вместе со значениями параметрических неизвестных образуют решение системы (1) . Легко видеть, что так мы получим все множество решений.

На формулах (5) можно было бы и остановиться, но ниже мы дадим более простое и наглядное, а также принципиально важное описание совокупности решений системы линейных уравнений.

Видео:Неоднородная система линейных уравненийСкачать

Приведенная система.

Сопоставим системе линейных уравнений (1) однородную систему с той же матрицей коэффициентов: tagAboldsymbol=boldsymbol. По отношению к системе (1) она называется приведенной.

Пусть boldsymbol_ — решение системы (1) . Столбец boldsymbol также будет ее решением тогда и только тогда, когда найдется такое решение у приведенной системы (6) , что boldsymbol=boldsymbol_+boldsymbol .

Пусть boldsymbol — решение системы (1) . Рассмотрим разность boldsymbol=boldsymbol-boldsymbol_ . Для нее Aboldsymbol=Aboldsymbol-Aboldsymbol_=boldsymbol-boldsymbol=boldsymbol .

Обратно, если boldsymbol — решение системы (6) , и boldsymbol=boldsymbol_+boldsymbol , то Aboldsymbol=Aboldsymbol_+Aboldsymbol=boldsymbol+boldsymbol=boldsymbol .

Это предложение сводит задачу описания множества решений совместной системы линейных уравнений к описанию множества решений ее приведенной системы.

Однородная система совместна. Действительно, нулевой столбец является ее решением. Это решение называется тривиальным.

Пусть столбцы матрицы A линейно независимы, то есть mathbf,A=n . Тогда система (6) имеет единственное решение (ранее мы это уже доказывали) и, следовательно, нетривиальных решений не имеет.

Если boldsymbol_ и boldsymbol_ — решения однородной системы, то любая их линейная комбинация — также решение этой системы.

Действительно, из Aboldsymbol_=boldsymbol и Aboldsymbol_=boldsymbol для любых alpha и beta следует A(alpha boldsymbol_+beta boldsymbol_)=alpha A boldsymbol_+beta Aboldsymbol_=boldsymbol .

Если однородная система имеет нетривиальные решения, то можно указать несколько линейно независимых решений таких, что любое решение является их линейной комбинацией. Сделаем это.

Матрица F , состоящая из столбцов высоты n , называется фундаментальной матрицей для однородной системы с матрицей А, если:

1. AF=O ;
2. столбцы F линейно независимы;
3. ранг F максимален среди рангов матриц, удовлетворяющих условию 1).

Столбцы фундаментальной матрицы называются фундаментальной системой решений.

Если фундаментальная матрица существует, то каждый ее столбец в силу первого условия определения — решение системы. Если система не имеет нетривиальных решений, то фундаментальной матрицы нет. Это будет в том случае, когда столбцы А линейно независимы: mathbf,A=n .

Ниже мы докажем, что в остальных случаях фундаментальная матрица существует, но сначала выясним, что означает третье условие в определении.

Пусть A — матрица размеров m times n и ранга r . Если AF=O , то mathbf,F leq n-r .

Приведем матрицу A к упрощенному виду элементарными преобразованиями строк, а затем элементарными преобразованиями столбцов обратим в нулевые все небазисные столбцы. Мы получим матрицу A’=PAQ , где P и Q — произведения соответствующих элементарных матриц. Первые r строк A’ — строки единичной матрицы порядка n , а остальные — нулевые. Обозначим F’=Q^F . Тогда mathbf,F’ = mathbf,F . Используя ранее доказанное нами утверждение, легко заметить, что первые r строк матрицы A’F’ совпадают с первыми r строками F’ . Но A’F’=PAF=O и, следовательно, F’ содержит r нулевых строк. Так как всего в ней n строк, mathbf,F’ leq n-r . Это равносильно доказываемому утверждению.

Покажем теперь, как может быть построена фундаментальная матрица. Согласно ранее доказанному утверждению, решение однородной системы состоит из коэффициентов равной нулю линейной комбинации столбцов матрицы системы. Мы можем получить такие линейные комбинации, основываясь на теореме о базисном миноре. Снова для удобства записи будем считать, что в матрице A первые r столбцов — базисные. Каждый из небазисных столбцов boldsymbol_ (j=r+1. n) раскладывается по базисным: tag boldsymbol_=alpha_^boldsymbol_+. +alpha_^boldsymbol_. Отсюда следует, что столбец begin -alpha_^. -alpha_^& 0. 0& 1& 0. 0 end^ решением. (Единица в нем стоит на j -м месте.)

Таких решений можно составить столько, сколько есть небазисных столбцов, то есть (n-r) . Убедимся в том, что эти решения линейно независимы. Для этого объединим все столбцы в одну матрицу tag begin -alpha_^& -alpha_^&. -alpha_^,\cdots\-alpha_^& -alpha_^&. -alpha_^,\1& 0&. & 0\0& 1&. & 0\cdots\0& 0&. & 1end.
Подматрица в последних n-r строках — единичная. Поэтому ранг матрицы (8) равен числу столбцов, и столбцы линейно независимы.

Таким образом, мы получили

Если ранг матрицы однородной системы линейных уравнений r меньше числа неизвестных n , то система имеет фундаментальную матрицу из n-r столбцов.

Итак, система столбцов (8) — фундаментальная система решений. Она называется нормальной фундаментальной системой решений. Каждому выбору базисных столбцов соответствует своя нормальная фундаментальная система решений. Вообще же, каждая система из n-r линейно независимых решений является фундаментальной.

Для нахождения матрицы (8) можно привести матрицу A системы к упрощенному виду, что даст коэффициенты разложения небазисных столбцов по базисным.

Пусть F — фундаментальная матрица системы Aboldsymbol=boldsymbol . Рассмотрим произвольный столбец с высоты n-r . Произведение Fboldsymbol — столбец высоты n , и из равенства AFboldsymbol =boldsymbol следует, что при любом с столбец Fboldsymbol — решение системы. Оказывается, имеет место

Столбец boldsymbol — решение системы Aboldsymbol=boldsymbol тогда и только тогда, когда существует такой столбец boldsymbol , что tag boldsymbol=Fboldsymbol.

Остается доказать необходимость условия. Пусть boldsymbol — решение. Присоединив его к F , получим матрицу F^=begin F | boldsymbol end . Эта матрица удовлетворяет условию AF^=O , так как каждый ее столбец — решение. Значит, mathbf,F^=n-r . По теореме Кронекера-Капелли мы заключаем отсюда, что существует столбец boldsymbol , удовлетворяющий системе Fboldsymbol=boldsymbol .

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Общее решение системы линейных уравнений.

Теперь мы можем собрать воедино наши результаты — утверждения 2 и 6.

Выражение, стоящее в правой части формулы (10) , называется общим решением системы линейных уравнений. Если boldsymbol_. boldsymbol_ — фундаментальная система решений, а c_. c_ — произвольные постоянные, то формула (10) может быть написана так: tag boldsymbol=boldsymbol_+c_boldsymbol_+. +c_boldsymbol_.

Теорема 3 верна, в частности, и для однородных систем. Если boldsymbol_ — тривиальное решение, то (10) совпадает с (9) .

Одна из ранее доказанных нами теорем гласит, что для существования единственного решения системы из n линейных уравнений с n неизвестными достаточно, чтобы матрица системы имела детерминант, отличный от нуля. Сейчас легко получить и необходимость этого условия.

Пусть A — матрица системы из n линейных уравнений с n неизвестными. Если det A=0 , то система либо не имеет решения, либо имеет бесконечно много решений.

Равенство det A=0 означает, что mathbf,A и, следовательно, приведенная система имеет бесконечно много решений. Если данная система совместна, то из теоремы 3 следует, что и она имеет бесконечно много решений.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Пример.

Рассмотрим уравнение плоскости как систему tagAx+By+Cz+D=0 из одного уравнения. Пусть A neq 0 и потому является базисным минором матрицы системы. Ранг расширенной матрицы 1, значит, система совместна. Одно ее решение можно найти, положив параметрические неизвестные равными нулю: y=z=0 . Мы получим x=-D/A . Так как n=3 , r=1 , фундаментальная матрица имеет два столбца. Мы найдем их, придав параметрическим неизвестным два набора значений: y=1 , z=0 и y=0 , z=1 . Соответствующие значения базисной неизвестной x , найденные из приведенной системы, будут -B/A и -C/A . Итак, общее решение системы (12) tag begin x\ y\ z end=begin -D/A\ 0\ 0 end+c_ begin -B/A\ 1\ 0 end+c_ begin -C/A\ 0\ 1 end.

Выясним геометрический смысл полученного решения. Очевидно, прежде всего, что решение begin -D/A& 0& 0 end^ состоит из координат некоторой (начальной) точки плоскости, или, что то же, из компонент ее радиус-вектора. В формуле (10) решение x_0 можно выбирать произвольно. Это соответствует произволу выбора начальной точки плоскости. Мы уже знаем, что компоненты лежащих в плоскости векторов удовлетворяют уравнению Aalpha_+Balpha_+Calpha_=0 , то есть приведенной системе. Два линейно независимых решения этой системы (фундаментальная система решений) могут быть приняты за направляющие векторы плоскости. Таким образом, формула (13) — не что иное, как параметрические уравнения плоскости.

Видео:Решение системы уравнений методом Крамера.Скачать

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Видео:Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

🌟 Видео

Теорема о количестве решений системы линейных уравненийСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Теорема Кронекера-КапеллиСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Математика это не ИсламСкачать

Теорема о структуре общего решения однородной системы линейных уравненийСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Фундаментальная система решений для однородной системы линейных уравненийСкачать

Видеоурок "Однородные системы линейных уравнений"Скачать