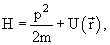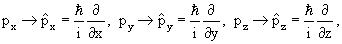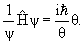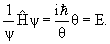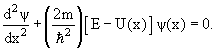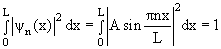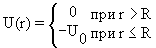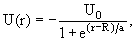Свободная частица, движущаяся вдоль оси х
Потенциальная энергия равна нулю: 
Введем волновой вектор 
и перепишем уравнение в виде
Существуют, как известно, два линейно независимых решения уравнения (4.22), так что общее решение есть суперпозиция двух волн — или стоячих:
или бегущих:
(первый член — волна бежит направо, второй — налево; постоянные 




При решении большинства задач квантовой механики следует обратить внимание на то, что волновая функция всегда должна быть непрерывной — вероятность пребывания частицы не может меняться скачком от точки к точке. Кроме того, если потенциальная энергия непрерывна или имеет скачки, но только первого рода (конечные скачки) и не имеет бесконечных скачков (скачков второго рода), то из уравнения Шредингера следует, что и первая производная волновой функции также непрерывна.
Частица в бесконечно глубокой потенциальной яме
Потенциальная энергия в этой задаче имеет вид
Такая система соответствует частице, движущейся вдоль прямой линии и отскакивающей от абсолютно отражающих препятствий в точках 






Общее решение имеет вид
Используем сначала первое граничное условие
Мы получили, что решение уравнения Шредингера должно иметь вид
Если продолжить нашу аналогию, то можно сказать, что на струне, закрепленной в одной точке, бегущих волн не бывает: отражение от неподвижной точки обязательно порождает стоячую волну. Однако на длину волны никаких ограничений не накладывается.
Теперь наложим второе из граничных условий:
Здесь есть два типа решений. При 
что означает отсутствие частицы в яме (вероятность найти ее всюду равна нулю). Поэтому нас интересует второе – нетривиальное – решение, когда
Это возможно лишь при некоторых значениях волнового вектора:
Так как энергия частицы связана с волновым вектором, то
Мы получили квантование энергии, то есть наша «струна», закрепленная с обеих сторон, зазвучала, так как появились выделенные частоты.
Подставляя найденные разрешенные значения волнового вектора в выражение для волновой функции, получаем ее в виде
Смысл квантового числа: оно на единицу больше числа нулей волновой функции. Значение постоянной
определяется из условия нормировки.
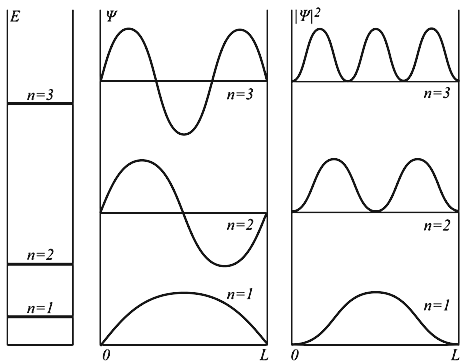
Рис. 4.8. Уровни энергии, волновые функции и распределение плотности вероятностей по координате x
Отметим, что значения 



Откуда же берется дискретность уровней энергии, характерная и для атома? Сравним со свободной частицей: уравнения те же, но с иными граничными условиями! Здесь возможны две постановки задачи. В первом случае исследуется состояние, которому в классической механике соответствовало бы инфинитное движение (задача рассеяния). Обычно в таких случаях решения возможны при любых значениях энергии (как говорят, спектр непрерывен). Во втором случае исследуется состояние, которому в классике соответствует финитное движение в ограниченной области пространства (задача на связанные состояния). Требование конечности волновой функции во всем пространстве ведет к квантованию энергии. Подчеркнем: в этом случае стационарное уравнение имеет физически приемлемые решения не всегда, а лишь при некоторых значениях энергии 
Пример. Определим разность соседних уровней энергии 



Используя выражение (4.24) для уровней энергии частицы в потенциальной яме, находим разность энергий соседних уровней
при больших значениях 
Приравнивая 
Уже само по себе это число говорит о том, что в области крайне высоких возбуждений работают классические формулы. Разность энергий соседних уровней получается, подстановкой в формулу для 
В электрон-вольтах те же характеристики имеют значения
Относительная разность энергий соседних уровней ничтожно мала:
и потому в классическом пределе квантовой дискретностью пренебрегают.
Частица в трехмерной потенциальной яме
Это обобщение предыдущей задачи. Частица может двигаться в кубическом объеме с длиной ребра 
Такая волновая функция соответствует очевидному факту, что движения вдоль трех осей не зависят друг от друга, и каждое описывается прежними одномерными волновыми функциями. Энергия, как легко догадаться, будет равна сумме энергий движения по осям x, y, z:
Рис. 4.9. Трёхмерная потенциальная яма
Состояние системы теперь определяется тремя квантовыми числами 





и ей соответствует одна волновая функция 
Но такую энергию имеют теперь три состояния с волновыми функциями 





и вырождение могло бы иметь место лишь при определенных соотношениях между длиной, шириной и высотой потенциального ящика.
Одномерный осциллятор
В классической физике пружинный маятник (одномерный осциллятор) представляет собой точечное тело массой m, прикрепленное к пружине и колеблющееся с круговой частотой 
так что уравнение Шредингера записывается в виде
Отсюда можно найти решение для волновой функции основного состояния
Подставляя это выражение в уравнение Шредингера, легко убедиться, что энергия основного состояния равна
Мы не выписываем волновые функции возбужденных состояний осциллятора, но выражение для разрешенных значений энергии имеет вид ( 
Здесь воспроизводится формула Планка и нулевые колебания

полученные ранее из соотношения неопределенностей (см. разд. 3.3).
Рис. 4.10. Уровни энергии и распределения плотности вероятностей по координате x для разных значений колебательного квантового числа. График потенциальной энергии осциллятора показан синей линией
Рис. 4.11. Распределения вероятностей для классического (пунктир) и квантового (сплошная линия) осцилляторов.
a) n = 1; б) большие значения n
Трехмерный осциллятор
Эта задача является обобщением предыдущей. Как и для трехмерной потенциальной ямы с бесконечно высокими стенками, волновая функция представляется в виде произведения волновых функций одномерных осцилляторов, колеблющихся независимо вдоль осей 


а уровни энергии трехмерного осциллятора описываются формулой
В отличие от одномерного осциллятора состояние определяется значениями трех квантовых чисел 


- Свободная частица уравнение шредингера и его решение для свободной частицы
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- РЕШЕНИЯ УРАВНЕНИЯ ШРЁДИНГЕРА ДЛЯ ПРОСТЕЙШИХ ЗАДАЧ
- Одномерная модель свободной частицы
- 🎥 Видео
Видео:Урок 455. Уравнение ШрёдингераСкачать

Свободная частица уравнение шредингера и его решение для свободной частицы
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
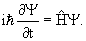 | (4.1) |
где 
в которой 







х → 


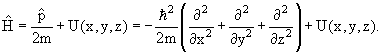 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


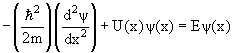
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
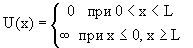 | (4.5) |
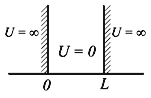
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
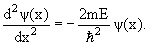 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
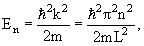 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
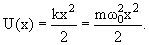 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
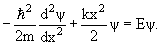 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
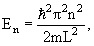

Одномерный гармонический осциллятор:
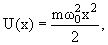
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
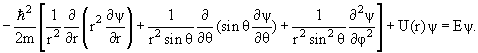 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
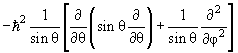 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 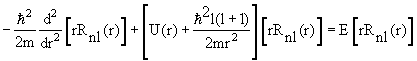 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
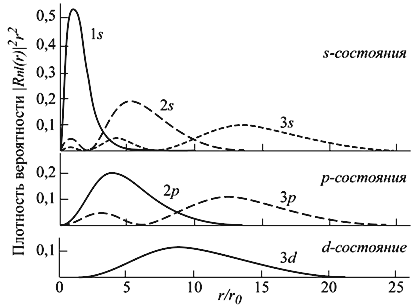
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
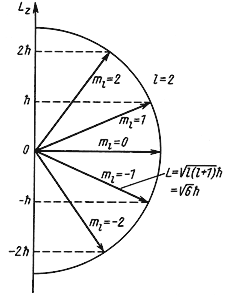
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
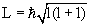 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
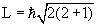
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Видео:97. Микрочастица в потенциальной ямеСкачать

РЕШЕНИЯ УРАВНЕНИЯ ШРЁДИНГЕРА ДЛЯ ПРОСТЕЙШИХ ЗАДАЧ
Рассмотрим простейшие примеры решения уравнения Шрёдингера для стационарных состояний, имеющие прямое отношение к химическим задачам. Существенное влияние на характер получаемых решений уравнения оказывают граничные условия задач. В частности, они определяют, будет ли спектр собственных значений гамильтониана дискретным или непрерывным.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Одномерная модель свободной частицы
Свободной называется частица, потенциальная энергия которой в любой точке пространства одинакова. Свободные электроны, например, образуются в процессах ионизации молекул. Они участвуют на первом этапе в реакциях захвата электронов.
Для удобства обычно считают, что U = 0. В этом случае одномерное уравнение Шрёдингера для стационарного состояния частицы, движущейся вдоль оси х, имеет вид
Введя обозначение k 2 = 2тЕ, получаем
Общее решение такого уравнения следующее:
где Cj и с2 — произвольные постоянные.
Общее решение есть линейная комбинация двух волн де Бройля, соответствующих импульсам рх и -рх.
Ограничимся рассмотрением одной волны, бегущей в положительном направлении оси х:
Условие нормировки данной функции стандартным образом получить не удается, так как интеграл
расходится. Чтобы осуществить нормирование функции, можно в качестве ограничения на свойства функции наложить условие ее периодичности:
где L — длина периодичности.
В принципе данное ограничение не является существенным, так значение L может быть выбрано сколь угодно большим. Теперь благодаря периодичности функции на отрезке L условие ее нормировки приобретает вид
Из условия периодичности находим 
Теперь благодаря использованной подстановке k 1 = 2тЕ выражение для энергии частицы и ее волновая функция приобретают более конкретный вид
Условие периодичности делает энергетический спектр частицы дискретным, однако при /,—>о спектр получается непрерывным.
🎥 Видео
Урок 456. Движение микрообъекта в одномерной бесконечно глубокой потенциальной ямеСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

свободная частица | одномерные задачи | задачи по квантовой механикеСкачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

10. Уравнение ШрёдингераСкачать

Урок 454. Понятие о волновой функцииСкачать

Петров С.В. - Квантовая механика - 7. Особенности решения уравнения ШредингераСкачать

Частица в одномерной потенциальной ямеСкачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Лекция №04 "Уравнение Шредингера"Скачать

QM_03 (Операторы импульса и энергии, уравнение Шредингера)Скачать

Петров С.В. - Квантовая механика - 6. Вырожденный спектр и уравнение ШредингераСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Лекции 5-6. Уравнение Шредингера и его приближенные решения. Межатомные.Скачать

Елютин П. В. - Квантовая теория I - Свойства решений стационарного уравнения ШредингераСкачать

Ишханов Б. С. - Физика атомного ядра и частиц - Уравнение Шредингера (Лекция 4)Скачать