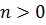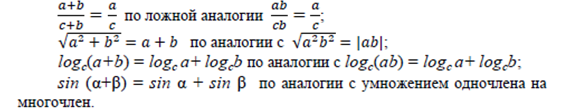Индукция и дедукция.
2.1. Определение индукции и дедукции.
Различают два вида рассуждений: индукцию и дедукцию.
Дедукция (от лат. deduction – выведение) или дедуктивный метод – способ рассуждения от общего к частному, от общих положений к частным заключениям. Например, применение любого из признаков делимости.
Индукция (от лат. induction – наведение) – способ рассуждения от частного к общему, от фактов к обобщениям. Например, установление признаков делимости на 10, 5, 3 и 2 в VI классе (индукция используется при выводе признаков: признаки делимости устанавливаются, исходя из наблюдения за таблицей умножения).
Индукция и дедукция не изолированы друг от друга, а находятся в диалектическом единстве. Всякая научная дедукция является результатом предварительного индуктивного изучения материала и применением индуктивно полученных результатов.
Индукция и ее виды.
Индуктивное умозаключение сложилось в процессе многовековой общественно-исторической и производственной практики и обязано своим происхождением наблюдению и опыту. Как разновидность вывода, индукция упомянута впервые в трудах древнегреческого философа Сократа (469 – 399 гг. до н. э.)
Термин «индукция» имеет три основных значения:
1) это один из видов рассуждений, при котором из двух или нескольких единичных (это S есть р) или частных (некоторое S есть p) высказываний получают новое общее высказывание (все S есть р).
2) это метод исследования, при котором желая изучить некоторое множество объектов (некоторых явлений), изучают отдельные объемы (обстоятельства), устанавливая в них те свойства, которые присущи всему рассматриваемому множеству объектов (или те обстоятельства, от которых зависит данное явление);
3) это форма изложения (беседа, процесс обучения), когда от менее общих положений приходят к общим положениям (заключениям, выводам).
Рассмотрим следующие примеры:
Пример 1.Единичные суждения: если дискриминант D квадратного уравнения с действительными коэффициентами больше нуля, то квадратное уравнение имеет два действительных корня; если D=0, то уравнение имеет один действительный корень; если D 0, D=0, D
Знакомя учащихся с высотой треугольника, учитель чертит на доске треугольники разных видов и в каждом из них ученики проводят по три высоты; из рассмотрения этих чертежей учащиеся приходят к выводу, что три высоты в остроугольном и прямоугольном треугольниках пересекаются в одной точке (она лежит внутри треугольника или совпадает с вершиной). А в тупоугольном треугольнике проходят через одну точку прямые, которым принадлежат высоты. Здесь индукция выступает в роли метода обучения.
Различают два основных вида индукции: неполную и полную. Неполная индукция (как метод исследования) – индукция, при которой не исчерпываются все частные случаи, относящиеся к данной ситуации.
Как отмечает Д. Пойа [3, с. 111], Л. Эйлер – мастер индуктивного исследования в математике, он сделал важные открытия с помощью индукции (о бесконечных рядах, в теории чисел и др. областях), т.е. с помощью наблюдения, дерзкой догадки и проницательных подтверждений. Однако Л. Эйлер в этом отношении не является единственным: другие математики, известные и менее известные, в своей работе также пользуются индукцией. Все же в одном отношении Л. Эйлер кажется почти единственным: он старается изложить относящиеся к вопросу индуктивные доводы заботливо, в деталях, в хорошем порядке. Он излагает их убедительно, но честно, как это подобает настоящему ученому. Его изложение является чистосердечным изложением идей, приведших его к этим открытиям, и имеет особую прелесть.
С точки зрения логики, неполной индукцией называется вывод, основанный на рассмотрении одного или нескольких (но не всех) единичных или частных суждений, относящихся к рассматриваемому понятию (или системе понятий). Например, законы арифметических действий в школе (переместительный, сочетательный и т.д.) изучаются с помощью неполной индукции.
Вывод, основанный на неполной индукции, может быть ошибочным, поэтому индукция в качестве метода исследования применяется весьма осторожно. Значение неполной индукции состоит в том, что рассмотрение частных случаев позволяет выявить закономерность, помогает высказать гипотезу о характере этой закономерности; доказательство же должно быть осуществлено другим путем (обычно дедукцией). Неполная индукция позволяет догадаться об идее доказательства перед тем, как проведете его в деталях.
В процессе обучения школьников к неполной индукции нужно относиться осторожно, учащиеся должны знать, что заключения по индукции могут быть и ложными, и истинными, они нуждаются в доказательстве. Но пренебрегать неполной индукцией нельзя, в этом методе реализуется принцип обучения «от простого к сложному», изучение новых абстрактных понятий и высказываний проходит естественным путем через опыт и наблюдение, через восприятие и представление и т.д. Кроме того, используя индуктивный метод обучения, мы обучаем учащихся математической деятельности, «наводим» самих учащихся на новое понятие, теорему или формулу. Но вывод надо делать на рассмотрении не одного, а нескольких частных случаев.
Полной индукцией называется вывод, основанный на рассмотрении всех единичных или частных суждений (случаев), относящихся к рассматриваемой ситуации. Если число этих случаев конечно и все они рассмотрены, то вывод, сделанный путем полной индукции, можно считать обоснованным.
Например, теорема об измерении вписанного угла, теорема косинусов.
Пример 4.В треугольнике ABC проведена высота СD. Какая из трех точек А, B и D лежит между двумя другими, если углы А и В треугольника острые. (Решение: точка В не может лежать между А и D, если бы она лежала между ними, то угол АВС был бы равен сумме углов ВСD и СDВ по теореме о внешнем угле треугольника, а значит острый угол В (по условию) был бы больше прямого. Точно так же точка А не может лежать между точками В и D. Значит, точка D лежит между точками А и В).
Дедукция и ее виды.
Дедукция есть форма вывода, при которой из одного общего или одного частного высказывания получают новое, менее общее или частное суждение. Дедуктивные процессы на строгом уровне описываются в исчислениях математической логики, а впервые теорию дедукции разработал Аристотель. Р. Декарт считал, что к познанию вещей человек приходит двумя путями: через опыт и с помощью дедукции, которую он называл умозаключением; опыт часто вводит нас в заблуждение, а дедукция избавляет нас от этого недостатка.
Дедуктивные выводы могут быть представлены следующими видами:
· Переход от более общего положения к менее общему или единичному.
· Переход от более общего положения к общему положению, ему подчиненному.
Сумма углов треугольника равна 180°, значит, сумма углов прямоугольного треугольника также равна 180°, поэтому сумма острых углов прямоугольного треугольника равна 90°.
· Переход утверждения одной общности к утверждению той же общности.
Пример 7.Область определения четной (нечетной) функции симметрична относительно точки 0. Множество всех точек, соответствующих натуральным числам, не симметрично относительно никакой точки. Вывод: никакая функция с областью определения N не является четной (нечетной).
· Переход от единичного положения к частному.
Число е – трансцендентное.
Число π – трансцендентное.
Некоторые иррациональные числа трансцендентны.
Математика является дедуктивной наукой. При строгом изложении любой математической дисциплины устанавливается система основных понятий и отношений (которые не определяются), затем конструируется система аксиом, связывающая эти понятия и отношения. На основе системы основных понятий, отношений и аксиом образуются новые понятия (которые определяются через известные понятия и отношения), и посредством правил вывода строятся новые теоремы и следствия из них, излагаемые в логической последовательности. Дедуктивное доказательство теорем характеризуется не только логической последовательностью шагов, но и обязательностью обоснования каждого шага ссылками на известные математические предложения, предшествующие рассматриваемым.
Как метод исследования дедукция характеризуется тем, что для получения нового знания о некотором объекте (понятии, свойстве) находят ближайший к данному объекту класс объектов (ближайшее родовое понятие) и применяют к этому объекту (понятию) существенные свойства этого класса объектов (признаки рода).
Например, изучая свойства прямоугольника, мы устанавливаем, что он есть параллелограмм, поэтому обладает всеми свойствами параллелограмма.
Дедукция может выступать в виде особой формы изложения материала в учебнике, как один из методов обучения, при котором от общих правил и положений приходят к менее общим или частным правилам или положениям. Например, применяя признаки подобия треугольника к рассмотрению конкретных задач, мы используем дедукцию.
В процессе развития математики индукция и дедукция не выступают изолированно: они тесно переплетаются между собой, часто бывают просто неразличимы. (Выводя из наблюдений признак делимости на 2, учащиеся пользуются индукцией, применяя его – дедукцией).
Метод математической индукции.
Особенно ярко взаимосвязь индукции и дедукции выступает при изучении математических предложений, доказываемых методом математической индукции.
Например, при выводе формулы бинома Ньютона.
1) Наблюдение и опыт:
2) гипотеза: очевидно, коэффициенты (a + b) n равны числам n-ой строки треугольника Паскаля.
3) обоснование (доказательство) – методом математической индукции.
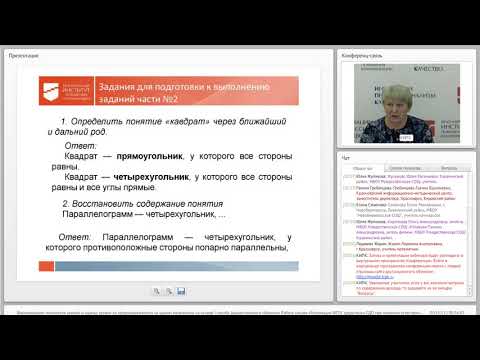
Метод математической индукции основан на так называемом принципе математической индукции: если какое-нибудь утверждение, сформулированное для натурального числа n, проверено для n=1 и из допущения его истинности для некоторого значения n = k следует его истинность для значения n = k + 1, то утверждение верно для любого натурального числа n.
Таким образом, метод математической индукции, применяемый к доказательству некоторой теоремы (формулы) обычно выглядит так:
1-й шаг. Проверяем истинность для п =1.
2-й шаг. Допускаем, что теорема верна для некоторого n = k и, исходя из этого допущения, доказываем истинность теоремы для n = k + 1
3-й шаг. На основании первых двух шагов доказательства и принципа математической индукции, заключаем, что теорема верна для любого натурального n.
1-й шаг. Проверяем истинность для n=1:
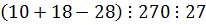
2-й шаг. Допускаем, что утверждение верно для некоторого n = k
и исходя из этого допущения, доказываем истинность утверждения для

= 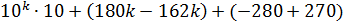
= 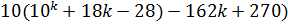
Так как первое слагаемое делится на 27 по предположению индукции, а второе и третье слагаемые делятся нацело на 27, то и вся сумма делится на 27.
3-й шаг. На основании того, что данное утверждение верно для n=1 и из предположения того, что оно верно для некоторого значения n = k, доказана его истинность для значения n = k + 1, данное утверждение верно для любого натурального числа n.
В математике доминируют дедуктивные умозаключения, хотя индуктивные методы играют существенную роль. В школьном обучении математике по сравнению с математической наукой удельный вес индуктивных методов значительно возрастает. Это определяется психологическим факторами педагогического процесса, невысоким начальным уровнем познавательных возможностей детей, постепенным и длительным процессом формирования их интеллекта. Соотношение между этими методами зависит от возраста школьников. Если в начальных классах преобладают индуктивные методы, то в старших классах – дедуктивные.
Еще в начале XX века опытные педагоги указывали, что только к 14-летнему возрасту школьники достигают той логической зрелости, которая позволяет понимать необходимость и сущность дедуктивных доказательств и оправдывает систематическое применение этого метода. Сейчас с дедуктивным методом учащиеся знакомятся примерно в 12 лет. Методисты считают, что трудности значительно уменьшились хотя бы потому, что в предыдущих классах теоретический уровень обучения и уровень математической подготовки школьников значительно повысился.
Аналогия.
Аналогия примыкает к неполной индукции. Если две вещи связаны одна с другой в одном или более признаках, и если некоторое высказывание истинно относительно одной из них, то оно, возможно, истинно и относительно другой. Схема заключения по аналогии: А обладает признаками с1, с2, …, сn. В обладает теми же признаками с1, с2, …, сn. А обладает признаком d, вероятно, и В обладает признаком d.
В планиметрии мы изучаем параллелограмм, в стереометрии аналогичной фигурой является параллелепипед. Противоположные стороны параллелограмма равны и параллельны, противоположные грани параллелограмма равны и параллельны. Диагонали параллелограмма, пересекаясь, делятся пополам, диагонали параллелепипеда – тоже. Наличие таких аналогичных свойств позволяет предположить, что эта аналогия распространяется и дальше. Так, сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Пробуя проверять аналогичное утверждение для параллелепипеда, убеждаемся, что у него сумма квадратов диагоналей равна сумме квадратов всех его ребер и т.д.
Но заключение по аналогии, как и неполной индукции, нуждается в доказательстве. Учащимся надо показать ряд примеров, когда аналогия может привести к грубым ошибкам.
В планиметрии можно построить бесконечное множество правильных многоугольников с каким угодно числом сторон, в стереометрии существует всего лишь 5 правильных многогранников. В планиметрии из всех многоугольников жестким является только треугольник (многоугольник называется жестким, если, будучи сделан из твердых негнущихся стержней, подвижно скрепленных в вершинах, он не может подвергнуться деформации). В стереометрии жестким является любой выпуклый многогранник (теорема Коши) (многогранник будет жестким, если, будучи сделан из твердых негнущихся пластинок, подвижно скрепленных в ребрах, он не может подвергнуться деформации).
В планиметрии один из двух равновеликих многоугольников всегда можно разрезать на такие треугольники, из которых можно сложить другой. В стереометрии один их двух равновеликих многогранников вообще нельзя разрезать на такие тетраэдры, из которых можно сложить другой (теорема Дена – Кагана).
Разница между аналогией и индукцией состоит в том, что в индукции происходит заключение от отдельных объектов к роду, в аналогии же – от объекта к объекту, от одного класса к другому классу. Вероятность заключения по аналогии зависит от того, насколько признаки с1, с2, …, сn, принадлежащие А и В, преобладают над различиями между А и В: чем больше общих свойств, чем меньше различий, тем больше вероятность правильного заключения. При этом признаки, являющиеся следствием некоторого признака, не принимаются во внимание. Если В обладает признаком, несовместимым с теми признаками, на основании которых делается заключение по аналогии, то общие признаки А и В не имеют значения, и вероятность заключения по аналогии равна нулю. Если d – следствие с1, с2, …, сn, то нет надобности заключения по аналогии.
Наиболее глубоко идущей аналогией, позволяющей делать безошибочные заключения, является изоморфизм. В случае изоморфизма каждое предложение, справедливое для одного множества объектов, можно полностью и без доказательства переносить на изоморфное множество объектов. Это обстоятельство дает возможность при наличии нескольких взаимно изоморфных множеств ограничиваться детальным рассмотрением только одного из них. Так в аналитической геометрии изучение свойств фигур сводится к изучению отношений между определенными уравнениями.
Аналогия является одним из эвристических методов в процессе математического развития: может подсказать существование нового предложения, способ доказательства или решения задачи. Понятие о функции комплексного переменного создано по аналогии с функцией действительного переменного, геометрия n-мерного пространства – по аналогии с 2-мерным или 3-мерным.
Но многие математические ошибки и заблуждения учащихся объясняются неверными аналогиями:
Учитель должен искоренять такие ошибки и предупреждать их появление (главное – добиваться ясного понимания основных понятий, знания содержания и объема понятия).
Контрольные вопросы и задания
1. Какие три основные значения имеет термин «индукция»?
2. Какие три основные значения имеет термин «дедукция»?
3. Разъясните суть метода неполной индукции, его преимущества и недостатки. Приведите пример (не из лекции).
4. Опишите схему применения метода математической индукции. Приведите пример (не из лекции).
5. Опишите схему рассуждения по аналогии. Приведите пример (не из лекции).
Видео:Теория вероятностей | Математика TutorOnlineСкачать

Дедуктивные и индуктивные умозаключения на уроке математики в начальной школе
студент факультета дошкольного, начального и специального образования, НИУ «БелГУ», г. Белгород, Россия
ДЕДУКТИВНЫЕ И ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ НА УРОКЕ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
Аннотация. В статье дается характеристика понятиям «дедуктивное умозаключение» и «индуктивное умозаключение», приводятся в пример задания, для решения которых необходимо использовать дедуктивные и индуктивные умозаключения, раскрываются возможности обучения младших школьников различным способам доказательств высказанных суждений.
В настоящее время актуальность умения строить дедуктивные и индуктивные умозаключения возросла. Оказывается, что осуществляемый процесс способствует развитию личности, а именно развитию определенных мыслительных процессов. Следовательно, обучение построению дедуктивных и индуктивных умозаключений должно быть одной из целей математического образования.
Всякое умозаключение представляет собой логическое следование одних знаний из других, в зависимости от характера этого следования, от направленности хода мысли. В умозаключении различают посылки — высказывания, представляющие исходное знание, и заключение — высказывание, к которому мы приходим в результате умозаключения [5, с. 85].
Дедуктивные умозаключения нам необходимы при изучении математики, методики ее преподавания и дидактики. В них мысль движется от общего к частному. В узком смысле слова, принятом в традиционной логике, под термином «дедукция» понимают дедуктивное умозаключение, то есть такое умозаключение, в результате которого получается новое знание о предмете или группе предметов на основании уже имеющегося некоторого знания о них, и применения к ним некоторого правила логики [5, с. 88].
На первый взгляд кажется, что использование дедуктивных умозаключений при обучении в начальных классах математике исключительно, так как не к каждой задаче можно применить этот метод. Но лишь благодаря дедуктивным умозаключениям воспитываются строгость, четкость и лаконичность мышления, поэтому без них при изучении начального курса математики нам никак не обойтись.
Для того чтобы учащиеся усвоили понятие «дедуктивные умозаключения» и легко могли использовать их при решении задач, необходимо на примерах объяснить процесс построения таких умозаключений, тем самым уделить больше времени этой теме и провести как можно больше подготовительных занятий. Начинать надо с самых элементарных заданий, при решении которых трудности могут возникнуть лишь у малой части класса. Как только у учащихся повысится скорость и правильность решения таких заданий, нужно приступать к более сложным заданиям, а именно к решению нестандартных математических задач.
Практика показывает, что для усвоения общих положений, правил, выводов учащимся требуется большое количество конкретных упражнений. Только в результате целенаправленной длительной работы в этом направлении появится возможность для благотворного развития логического мышления младших школьников [3, с. 38].
Математическая логика сложна для понимания учащихся, но им было бы легче ее усвоить благодаря интересным и занимательным заданиям, которые дети с удовольствием выполняли бы и которые послужили бы подготовительными занятиями для решения нестандартных задач. Приведем некоторые задания для примера:
Ответьте, верно ли составлено данное рассуждение (умозаключение), если нет, то почему?
Гитара – это музыкальный инструмент. У Андрея дома музыкальный инструмент. Значит, у него дома гитара. Классные комнаты надо проветривать. Квартира – это не классная комната. Значит, ее не надо проветривать. Умножение – это сложение одинаковых слагаемых. В примере 10+10+10+10+10 все слагаемые одинаковые. Значит сумма 10+10+10+10+10 – это произведение 10*5.
Можно использовать также задания на продолжение рассуждений, например:
Закончи следующие рассуждения:
Домашние животные полезны. Корова и коза – домашние животные. Все деревья растения. Дуб и осины растения. Если одно число при счете называют раньше, чем другое, то это число меньше. При счете 4 называют раньше 6.
При решении простых задач на разностное сравнение имеет смысл тоже обращаться к дедуктивным рассуждениям, используя наглядность только на этапе проверки решения задачи. Например: У Димы было 7 марок, у Антона 3 марки. На сколько марок больше у Димы, чем у Антона? Учащиеся рассуждают так: «Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее (общая посылка). В задаче нужно узнать, на сколько марок больше у Димы, чем у Антона (частная посылка). Умозаключение: значит, нужно из марок Димы вычесть марки Антона.
Благодаря этим заданиям у детей происходит обобщение учебного материала, понимание общих принципов и законов, лежащих в основе изучаемых математических фактов, и осознание тех связей, которые существуют между рассматриваемыми явлениями [1, с. 28].
Также учителя обязательно должны формировать у учащихся умение рассуждать. Это умение развивается с годами: чем старше ребенок и чем лучше была организована учителем его специальная учебная деятельность, тем правильнее и увереннее ученик будет рассуждать, делать вывод, исходя из каких-либо данных положений.
Особенность дедуктивных рассуждений в начальных классах заключается прежде всего в их тесной взаимосвязи с индуктивными. Так, методы и приемы обучения младших школьников на этапе усвоения новых знаний в большинстве случаев связаны с индуктивными рассуждениями. Поэтому учителю начальных классов необходимо, во-первых, иметь четкое представление о том, что такое индуктивные рассуждения (умозаключения), во-вторых, осознавать значение данного вида рассуждений для организации познавательной деятельности школьников, в-третьих, методически грамотно осуществлять руководство этой деятельностью [2, с. 145].
Слово «индукция» в переводе на русский язык означает – «наведение». Уже сам перевод этого слова говорит о дидактических возможностях данного метода: выводы, получаемые индуктивным путем, связаны с наблюдением, анализом, сравнением, с выявлением общих закономерностей и их последующим обобщением. Используя этот метод, учитель как бы ведет учащихся к цели, «наводит» их на нее.
Индуктивное умозаключение — это такое, в результате которого на основании знания об отдельных предметах данного множества (или об отдельных подмножествах данного множества) получается общий вывод, содержащий какое-либо знание обо всех предметах данного множества [5, с. 91].
Учить подмечать закономерности, сходное и различное следует начинать с простых упражнений, постепенно усложняя их с этой целью целесообразно предлагать серии упражнений с постепенным повышением уровня трудности [2, с. 175]. Способность подмечать закономерности развивается у учащихся в том случае, если подобранные упражнения доступны ребенку, и он может самостоятельно их выполнить. В этом случае развивается математическая наблюдательность, создаются условия для самостоятельной поисковой деятельности.
Уже в 1 классе можно предлагать учащимся задания, направленные на развитие наблюдательности, которая тесно связана с такими приемами логического мышления, как анализ, сравнение, синтез обобщение [4, с. 60].
Например: Продолжите данный ряд чисел 3, 5, 7, 9, 11, …
Во 2 и 3 классе предложить можно ученикам различные задания для самостоятельного выявления ими закономерностей связей и зависимостей и формулировки обобщения. Для этой цели используют задания вида сравнить примеры, найти общее и сформулировать новое правило [4, с. 62].
0+1, 2+3, 3+4, 4+5, 5+6, 6+7, 7+8, 8+9
Вывод: «Сумма двух последовательных чисел есть число нечетное».
7+2−2, 21+5−5, 34+6−6, 42−8+8 и т. д.
Вывод: «Если к любому числу прибавить и затем вычесть из него одно и то же число, то получится первоначальное число».
16:4∙4, 21:7∙7, 25:5∙5, 42:6∙6, 56:8∙8 и т. д.
Вывод: «Если любое число разделить и умножить на одно и то же число, то получится первоначальное число».
В процессе обучения индуктивным рассуждениям полезно побуждать учащихся к поискам новых примеров, подтверждающих правильность сделанного вывода и, с другой стороны, учить их сопоставлять вывод с теми фактами, на основе которых он сделан, искать и такие факты, которые могут опровергнуть сделанный вывод. В этих целях может оказаться полезным и прием специального столкновения учащихся с такими случаями, когда получаемый вывод оказывается неверным. Например, можно предлагать задания, в которых индуктивные рассуждения приводят к неправильному выводу:
Слагаемое 1 2 3 4 5 6
Слагаемое 5 5 5 5 5 5
Сумма 6 7 8 9 10 11
Получаемый вывод: «Сумма всегда больше каждого из слагаемых» − опровергается подбором таких фактов:
1+0=1, 2+0=2, и т. д., где сумма равна другому слагаемому, если одно из слагаемых равно 0 [4, с. 64].
Исходя из этого, можно сделать вывод, что использование индуктивного метода обучения при изучении курса математики в начальной школе способствует активному и сознательному усвоению знаний и положительно влияет на развитие учащихся.
Таким образом, мы выяснили, что, используя дедуктивные и индуктивные умозаключения при решении задач, мы тем самым развиваем логическое мышление школьников, учим детей правильно мыслить, аргументировать и доказывать, что важно и необходимо. Необходимо с помощью различных методов обучения активизировать творческую деятельность школьников на уроках математики. Поэтому использование учителем начальной школы дедукции и индукции при решении математических задач, является не только желательным, но даже обязательным элементом обучения математике. Мы показали, что существует много возможностей использовать дедуктивные и индуктивные умозаключения в начальных классах, это необходимо, так как именно они воспитывают строгость, четкость и лаконичность мышления.
Формирование приемов умственной деятельности у младших школьников / . — Ялта: КГГИ, 2001. — 34 с. Методика обучения математике в начальных классах / . — М.: Академия, 2001. — 288 с. Липина И. Развитие логического мышления на уроках математики / И. Липина // Начальная школа. — 1999. — № 8. — С. 37-39. Математика. Развитие логического мышления / . — Волгоград: Учитель, 2009. — 131 с. Логика. Учебно-методическое пособие / . — М.: МФЮА, 2006. — 121 с.
Видео:Педагогические ситуации в деятельности учителя, их виды и способы разрешенияСкачать

«Индуктивные и дедуктивные рассуждения, способы доказательства утверждений при решении задач как способ развития мышления младших школьников»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Антоненкова Е.Ю. 19 декабря 2014г.
«Индуктивные и дедуктивные рассуждения, способы доказательства утверждений при решении задач как способ развития мышления младших школьников»
“ Знание только тогда знание, когда оно
приобретено усилиями твоей мысли, а не памяти”.
В методической литературе можно встретить различные классификации способов решения задач. Но большинство выделяют следующие способы решения задач:
Арифметический. Результат решения задачи находится путем выполнения арифметических действий.
Алгебраический. Ответ находится путем составления и решения уравнения.
Графический. Позволяет найти ответ без выполнения арифметических действий, опираясь только на чертеж.
Практический (предметный). Ответ находится с помощью непосредственных действий с предметами.
При индуктивных рассуждениях мы собираем факты и используем их для подтверждения или опровержения своих заключений или гипотез.
При дедуктивных рассуждениях мы начинаем с утверждений, которые являются или считаются истинными.
Примером одного из первых дедуктивных умозаключений в начальном обучении математике является рассуждение: «2
Процесс решения задач оказывает положительное влияние на умственное развитие детей.
Поэтому важно, чтобы учитель имел глубокое представление о текстовой задаче, о ее структуре, умел решать задачи различными способами.
Аналитический метод решения задачи представляет собой стройную логическую цепь заключений, органически связанных между собой. Аналитический метод характеризуется тем, что рассуждения начинаются с вопроса задачи.
Таким образом, в основе данного метода решения задачи лежит умении строить дедуктивные рассуждения (от общего к частному). В дедуктивных рассуждениях нельзя получить ложное заключение из истинных посылок. Именно поэтому дедуктивные рассуждения используются в математических доказательствах.
Дедуктивные рассуждения используются, как правило, при решении задач на активный подбор вариантов отношений.
Анализ задачи состоит в том, что мы предполагаем её уже решенной и находим различные следствия этого решения, а затем, в зависимости от вида этих предположений, пытаемся найти путь отыскания решения поставленной задачи.
Процесс обучения младших школьников способам указанных математических доказательств и развития математической речи имеет большой потенциал для развития коммуникативных универсальных учебных действий младших школьников. Литература. А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская, О. А. Карабанова, Н. Г. Салмина, С. В. Молчанов. Как проектировать универсальные учебные действия в начальной школе: от действия к мысли: пособие для учителя / [А.Г. Асмолов, Г.В. Бурменская, И.А. Воло¬дарская и др.]; под ред. А.Г. Асмолова. — М. : Просвещение, 2008. — 151 с.
Краткое описание документа:
Антоненкова Е.Ю. 19 декабря 2014г.
«Индуктивные и дедуктивные рассуждения, способы доказательства утверждений при решении задач как способ развития мышления младших школьников»
“ Знание только тогда знание, когда оно
приобретено усилиями твоей мысли, а не памяти”.
В методической литературе можно встретить различные классификации способов решения задач. Но большинство выделяют следующие способы решения задач:
Арифметический. Результат решения задачи находится путем выполнения арифметических действий.
Алгебраический. Ответ находится путем составления и решения уравнения.
Графический. Позволяет найти ответ без выполнения арифметических действий, опираясь только на чертеж.
Практический (предметный). Ответ находится с помощью непосредственных действий с предметами.
При индуктивных рассуждениях мы собираем факты и используем их для подтверждения или опровержения своих заключений или гипотез.
При дедуктивных рассуждениях мы начинаем с утверждений, которые являются или считаются истинными.
Примером одного из первых дедуктивных умозаключений в начальном обучении математике является рассуждение: «2
Процесс решения задач оказывает положительное влияние на умственное развитие детей.
Поэтому важно, чтобы учитель имел глубокое представление о текстовой задаче, о ее структуре, умел решать задачи различными способами.
Аналитический метод решения задачи представляет собой стройную логическую цепь заключений, органически связанных между собой. Аналитический метод характеризуется тем, что рассуждения начинаются с вопроса задачи.
Таким образом, в основе данного метода решения задачи лежит умении строить дедуктивные рассуждения (от общего к частному). В дедуктивных рассуждениях нельзя получить ложное заключение из истинных посылок. Именно поэтому дедуктивные рассуждения используются в математических доказательствах.
Дедуктивные рассуждения используются, как правило, при решении задач на активный подбор вариантов отношений.
Анализ задачи состоит в том, что мы предполагаем её уже решенной и находим различные следствия этого решения, а затем, в зависимости от вида этих предположений, пытаемся найти путь отыскания решения поставленной задачи.
Процесс обучения младших школьников способам указанных математических доказательств и развития математической речи имеет большой потенциал для развития коммуникативных универсальных учебных действий младших школьников. Литература. А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская, О. А. Карабанова, Н. Г. Салмина, С. В. Молчанов. Как проектировать универсальные учебные действия в начальной школе: от действия к мысли: пособие для учителя / [А.Г. Асмолов, Г.В. Бурменская, И.А. Воло¬дарская и др.]; под ред. А.Г. Асмолова. — М. : Просвещение, 2008. — 151 с.
💥 Видео
Как научить ребенка решать задачи по математике. Почему не получается решать задачи по математике?Скачать

Краткая запись задачи. Как сделать краткую запись к задаче?Скачать

Нестандартные способы решения уравнений, неравенств, систем в 10-11 классахСкачать

Методы решения текстовых задач в школьном курсе математики. 5-9 классыСкачать

Эффективность урока – стимул к успеху учителя и ученика | Видеолекции | ИнфоурокСкачать

Как научить вашего ребенка решать задачи. Методика обучения решению задач. Методика ШаталоваСкачать

Дифф. уравнения. Консультация перед письменным экзаменом, Голубев М.О.Скачать

Основы методики обучения математике (Шилинг Г.С.)Скачать

Методика обучения решенипю текстовых задач, основанная на УУД моделирования, позволяющаяСкачать

Решение текстовых задач по математикеСкачать

Паршина Е.С. Моделирование на уроках математики в начальной школеСкачать

Как сделать урок математики интересным? Урок математики в начальной школе. Школа молодого учителяСкачать

Математика - консультация перед вступительным испытаниемСкачать

Алгебраическая составляющая ОГЭСкачать

Как построить новый способ? (структура II этапа учебной деятельности)Скачать

Олимпиадная математика в начальной школеСкачать

Метапредметный подход в проведении учебных занятий по математике | Видеолекции | ИнфоурокСкачать

Формирование логических умений и оценка уровня их сформированности на уроках мСкачать