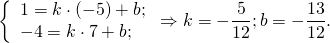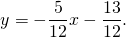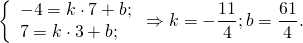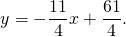Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Видео:Уравнения стороны треугольника и медианыСкачать
Задача 41259 Найти уравнение сторон треугольника.
Условие
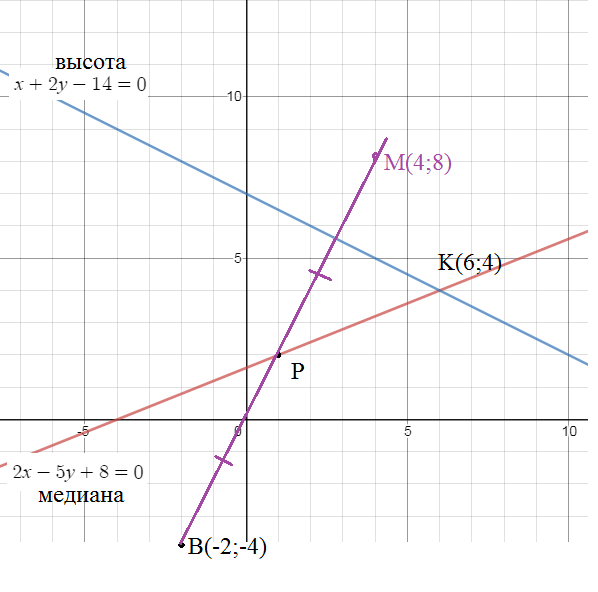
Найти уравнение сторон треугольника, если известны одна из вершин В(-2;-4) и уравнение медианы 2х-5у+8=0 и высоты х+2у-14=0 проведеденных из этой вершины
Все решения
Найдем координаты точки пересечения медианы и высоты:
<2x-5y+8=0
<x+2y-14=0
Назовем ее точка К
Скорее всего дана точка В и два уравнения медианы и высоты,
проведенных из других вершин треугольника
Составим уравнение прямой ВК, как прямой проходящей через две точки:
х+2=y+4
[b]x-y-2=0 [/b]- уравнение ВК
высота x+2y-14=0 и ВК не перпендикулярны,так как произведение угловых коэффициентов взаимно перпендикулярных прямых должно быть равно (-1).
Значит высота перпендикулярна стороне ВМ.
Координату точки М требуется найти
Уравнение стороны ВМ, как прямой, перпендикулярной x+2y-14=0
и проходящей через точку В легко написать.
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
Значит, угловой коэффициент стороны ВМ
k_(BM)=2
Общий вид такой прямой
y=2x+b
Так как ВМ проходит через точку В, подставим ее координаты в уравнение
y=2x+b
и найдем b
уравнение BM: [b]y=2x[/b]
Найдем координаты точки пересечения ВМ и медианы.
Решаем систему уравнений:
<2х–5у+8=0
<y=2x
Пусть это точка Р(1;2)
Уравнение КМ, как уравнение прямой проходящей через две точки:
[m]frac<x-x_><x_-x_>=frac<y-y_><y_-y_>[/m]
[b]2х+у-8=0[/b] — уравнение МК
О т в е т. x-y-2=0; y=2x; 2х+у-8=0 
Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Видео:Вычисляем высоту через координаты вершин 1Скачать
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
🎥 Видео
найти уравнение высоты треугольникаСкачать
Уравнение прямой и треугольник. Задача про высотуСкачать
№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать
Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
Высота, биссектриса, медиана. 7 класс.Скачать
Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать
Построение высоты в треугольникеСкачать
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Как найти медиану, зная стороны треугольника? Удвоение медианы.Скачать
Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать
Как находить медианы и высоты треугольника || ЕГЭ-2022 || ОГЭ - 2022Скачать
Длина медианы треугольникаСкачать
Аналитическая геометрия на плоскости. Решение задачСкачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
Построение медианы в треугольникеСкачать
