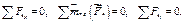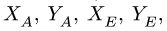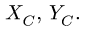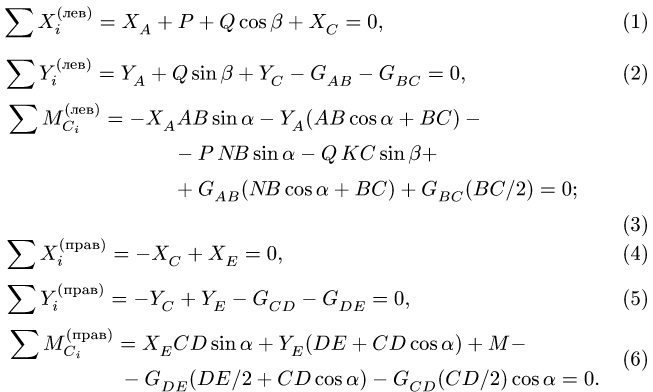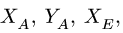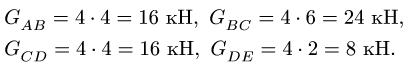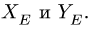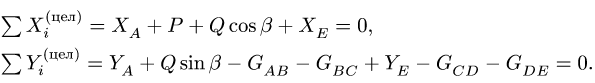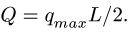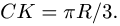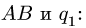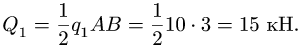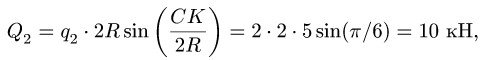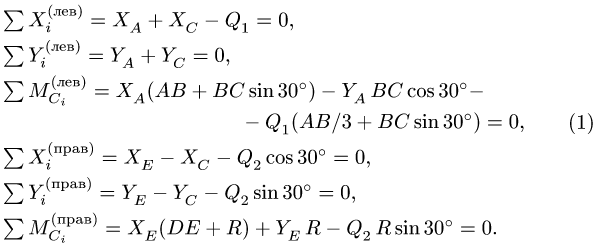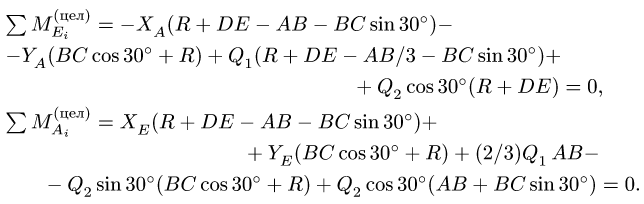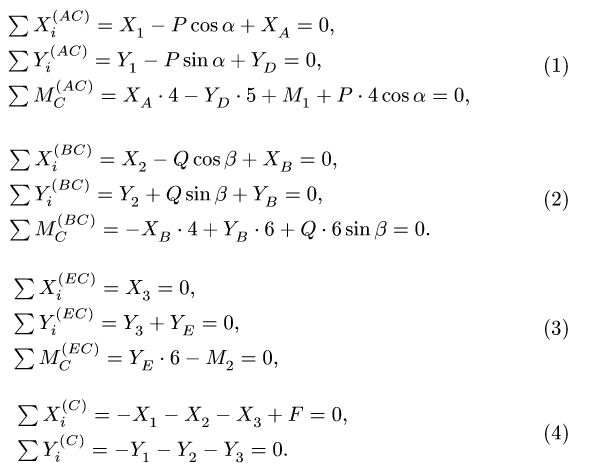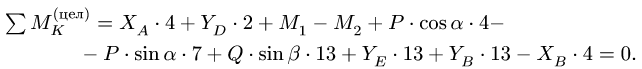Составить уравнение равновесия составной конструкции (7 видео)

Определение реакций опор составной конструкции – решение задачи

Содержание

Как определить реакции опор составной конструкции
Пример решения задачи на определение реакций опор составной конструкции
Решение задачи
Равновесие стержня CB
Равновесие конструкции в целом
Решение уравнений равновесия
Проверка правильности решения
Равновесие составной конструкции
Расчет составной конструкции в теоретической механике
Конструкция с распределенными нагрузками
Расчет системы трех тел, соединенных шарниром
🎦 Видео

Видео:Определение реакций опор простой рамыСкачать

Как определить реакции опор составной конструкции

Для определения реакций опор составной конструкции, мы выполняем следующие шаги.

Мысленно разбиваем конструкцию на отдельные элементы, каждый из которых является твердым телом или материальной точкой.
Вместо связей в опорах и точках соединений составных элементов прикладываем силы реакций. Вид сил реакций зависит от крепления опоры или точки соединения тел.
Для каждого тела, входящего в конструкцию, составляем уравнения равновесия.
В результате получаем систему уравнений. Если задача является статически определимой, то эта система имеет единственное решение. Решаем ее, и получаем искомые значения реакций опор и сил реакций, действующих между отдельными элементами конструкции.
Если задача не является статически определимой, то система уравнений имеет бесконечно много решений. Выбрать единственное решение, методами статики, нельзя. Это можно сделать методами сопротивления материалов.

При составлении уравнений стоит заметить, что иногда целесообразно составлять уравнения равновесия для всей конструкции в целом, или к группе ее элементов, рассматривая их как единое целое.

Силы, возникающие в точках соприкосновения частей конструкции, связаны между собой законом равенства действия и противодействия:
Сила, с которой первое тело действует на второе, равна по абсолютной величине и противоположна по направлению силе, с которой второе тело действует на первое.

Методы определения реакций опор твердых тел рассмотрены на странице
«Определение реакций опор твердого тела».

Далее рассмотрен пример решения задачи на определение реакций опор составной конструкции.

Видео:Определение реакций опор простой рамыСкачать

Пример решения задачи на определение реакций опор составной конструкции

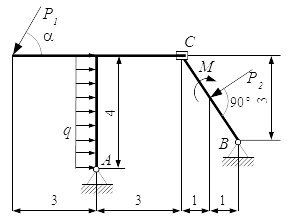
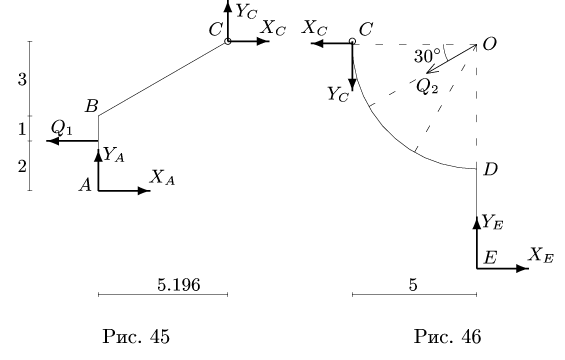
Для составной конструкции, изображенной на рисунке, определить реакции опор в шарнирах A и B , а также реакции в скользящей заделке C . Расстояния указаны в метрах.

Дано:
P ₁ = 5 kН ; P ₂ = 7 kН ; M = 22 kН·м ; q = 2 kН/м ; α = 60° .

Решение задачи

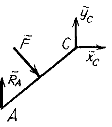
Равновесие стержня CB

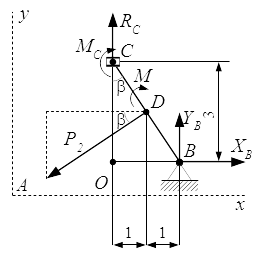
Мысленно разъединим конструкцию. Рассмотрим равновесие стержня CB . Проводим систему координат Axyz с началом в точке A . Ось Az перпендикулярна плоскости рисунка и направлена на нас.

Соединение в точке C является скользящей заделкой. Заменим это соединение силами реакций. Разложим их на две составляющие: на силу , параллельную оси y ; и на момент (пару сил) M_C . Их направления выбираем произвольно. Если мы не угадаем с направлением, то значение соответствующей реакции будет иметь отрицательное значение.

Шарнирную опору в точке B заменим силами реакций и , параллельными осям координат.

Рассмотрим геометрию системы. Из прямоугольного треугольника OBC имеем:
м ;
м ;
;
.
Здесь β – угол между стержнем CB и вертикалью CO . Поскольку , то угол между направлением силы и горизонталью также равен β .

Составляем уравнения равновесия. Сумма проекций сил на ось x равна нулю.
;
;
;
(П1) .

Сумма проекций сил на ось y равна нулю.
;
;
;
(П2) .

Составляем уравнение для моментов. Возьмем ось Bz′ , проходящую через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой оси равна нулю:
;
(П3.1) .

Вычисляем моменты сил. Ось Bz′ направлена на нас. По правилу правого винта, положительным направлением моментов сил является направление против часовой стрелки.
Силы реакций пересекают ось Bz′ . Поэтому их моменты равны нулю.
Плечом силы является отрезок OB . Тогда
.
Поскольку , то отрезок DB является плечом силы . Момент этой силы:
.

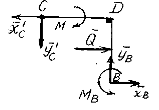
Равновесие конструкции в целом

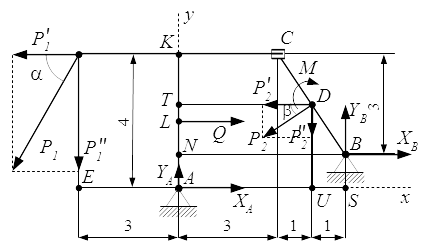
Рассмотрим равновесие всей конструкции в целом. Шарнирную опору в точке A заменим силами реакций и , параллельными осям координат.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
kН .
Точка приложения равнодействующей находится в центре тяжести эпюры – в точке L , посередине отрезка KA :
|KL| = |LA| = 2 м .

Силы и разложим на составляющие вдоль осей координат:
; ;
; ;
; .

Составляем уравнения равновесия. Сумма проекций сил, действующих на всю конструкцию, на ось x равна нулю.
;
;
;
(П4) .

Сумма проекций сил на ось y равна нулю.
;
;
;
(П5) .

Сумма моментов сил относительно оси z , проходящей через точку A перпендикулярно плоскости рисунка, равна нулю:
;
(П6.1)
.

Вычисляем моменты сил. Силы реакций и пересекают ось Az . Поэтому их моменты равны нулю.
Момент от некоторой силы относительно оси Az равен произведению плеча силы на абсолютное значение этой силы, взятое с соответствующим знаком. Если сила направлена в положительном направлении (против часовой стрелки), то знак момента положительный. В противном случае – отрицательный. Чтобы найти плечо, через вектор силы проводим прямую. Длина перпендикуляра, опущенного из точки A на эту прямую равна плечу силы относительно оси Az .

В результате уравнение (П6.1) принимает вид:

;
(П6)
.

Решение уравнений равновесия

Итак, мы получили следующую систему линейных уравнений:
(П1) ;
(П2) ;
(П3) ;
(П4) ;
(П5) ;
(П6)
.
В ней шесть уравнений и шесть неизвестных. Решаем систему.

Из уравнения (П1): kН .
Из уравнения (П4) имеем:

kН .
Из уравнения (П6) находим:

kН .
Далее из уравнений (П2), (П3) и (П5) последовательно находим:
kН .
kН .
kН .

Решение системы уравнений оказалось простым во многом благодаря тому, что мы подходящим образом выбрали оси, относительно которых вычисляли моменты. А также за счет того, что мы удачно выбрали части конструкции, для которых составляли уравнения (правую часть и всю конструкцию в целом). Можно составить уравнения равновесия и другими способами. Например, можно составить уравнения равновесия для левой и правой частей конструкции и выбрать другие оси для вычисления моментов. Если бы мы сделали это неудачно, то нам пришлось бы решать систему из шести линейных уравнений с шестью неизвестными другим способом, например, методом Крамера. Количество вычислений было бы больше, но в результате мы все равно получили бы одни и те же значения сил реакций.

Проверка правильности решения

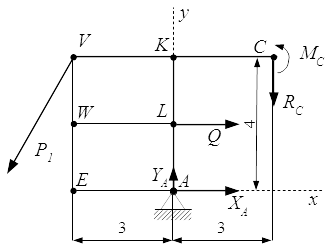
Сделаем проверку правильности решения задачи. Для этого рассмотрим равновесие левой части конструкции.

По закону равенства действия и противодействия, в скользящей заделке C , на раму действуют сила и момент M_C . Их направления противоположны силе и моменту, действующих в точке C на правую часть конструкции, а абсолютные значения равны.

Через точку V проведем ось Vz′′ , перпендикулярно плоскости рисунка. Если мы определили значения реакций правильно, то сумма моментов сил относительно этой оси должна равняться нулю:

kН ; kН ; kН ; kН ; kН ; kН·м .

Отрицательные значения реакций и указывают на то, что они направлены в сторону, противоположную той, которая изображена на рисунке.

Использованная литература:
Сборник заданий для курсовых работ по теоретической механике, под редакцией проф. А.А. Яблонского, Москва «Интеграл-пресс», 2006.

Автор: Олег Одинцов . Опубликовано: 08-11-2017 Изменено: 22-12-2021

Видео:Задача о составной конструкцииСкачать

Равновесие составной конструкции

Рассмотрим равновесие системы сил, которые приложены к системе тел, соединенных между собой с помощью шарниров, гибких звеньев (тросов), или таких, которые свободно опираются друг на друга. Силы, действующие на такую систему тел, можно разделить на внешние и внутренние.

Внутренние – силы взаимодействия между телами конструкции.

Внешние – силы, с которыми взаимодействуют тела данной конструкции с другими телами.

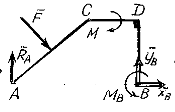
Пример. Конструкция состоит из двух твердых тел АС и СДВ, связанных между собой шарниром С (рис. 5.4 а). На конструкцию действует сила , пара сил с моментом М и равномерно распределенная нагрузка интенсивностью q. Для этой конструкции шарнир С – внутренняя связь, а связи, которые присоединяют конструкцию к земле – внешние (шарнир подвижный в точке А и жесткое защемление в точке В).

Определить реакции связей в точках А и В и усилие в шарнире С.


а	б

в	г
Рисунок 5.4

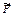
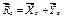
Если объектом изучения взять всю составную конструкцию как абсолютно твердое тело, воспользовавшись аксиомой затвердения (Дополнение А.2) – имеем схему сил, изображенную на рис. 5.4 б. Кроме заданных внешних силовых факторов: силы , момента М, силы , изображаем реакцию подвижного шарнира А- , направленную вверх (табл. 1.1, п. 4), реакцию жесткого защемления неизвестного направления разложим на две составляющие и добавим момент пары силы М_В (табл.1.1, п. 5). Таким образом, имеем четыре неизвестных. На конструкцию действует произвольная плоская система сил. На первый взгляд может показаться, что задача статически неопределенная, потому что уравнений равновесия – три; условие (5.10) не выполнено (4>3).

Но из-за того, что конструкция в шарнире С собрана из двух твердых тел АС и СДВ, за объекты изучения можно взять каждую из частей АС и СДВ. Тогда внутреннюю силу реакции шарнира С мы «переведем» в класс внешних сил. При этом воспользуемся аксиомой действия и противодействия (Дополнение А.2) (III-й закон Ньютона). На рисунках 5.4 в и 5.4 г показаны схемы сил, которые действуют на тела АС и СДВ. Это – произвольные плоские системы сил.

Дальше, для схем сил, изображенных на рисунках 5.4 в и 5.4 г, составляем по три уравнения равновесия. Начать лучше из уравнений для схемы 5.4 в, потому что три неизвестные 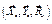легко определить из трех уравнений равновесия (5.5):

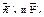
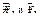
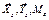
Потом, учитывая, что алгебраические значения равняются алгебраическим значениям , соответственно, составляем уравнения равновесия для схемы сил, которая действует на тело СДВ. Теперь имеем три новых неизвестных . Удачными для их определения будут уравнения равновесия (5.5)

Таким образом, в случае, когда конструкция составлена из нескольких, например n тел, статическую определенность задачи, вместо формулы (5.10) определяем формуле

где S – общее количество неизвестных;

lі – количество уравнений равновесия для і – го тела;

n – количество тел, из которых состоит конструкция.

Вывод: задачи на равновесие системы тел можно решать двумя методами.

Первый метод. Сначала рассматривается равновесие конструкции составленной из системы тел, считая, что внутренние связи затвердели (аксиома затвердения, Дополнение А.2). Позже рассматривается равновесие n –1 тел, из которых составлена конструкция. Составляется необходимое для определения неизвестных сил количество уравнений равновесия, руководствуясь условием статической определенности задачи (формула (5.11)).

Второй метод. Применяя метод разбиения конструкции на части, рассматривается равновесие каждого тела, из которых составлена конструкция. Для каждого тела составляется соответствующее количество уравнений равновесия. Этот метод применен в вышеприведенном примере.

Каким методом пользоваться? Оба методы – равноправные. Можно порекомендовать пользоваться вторым методом, если нужно определить усилия в соединительных элементах. Если спрашивают реакции только внешних связей – пользуются первым методом.

План решения задач вторым методом.

1. На рисунке изображают все заданные силы, которые действует на составную конструкцию. Согласно аксиоме связей (п. 1.4), «отбрасывают» внешние связи, заменяя их соответствующими реакциями связей (табл. 1.1).

2. Выяснив, что количество неизвестных больше количества уравнений равновесия, (которые можно составить для изображенной на рисунке системы сил) конструкцию разбивают на части, из которых она составлена. На следующих рисунках изображают схемы сил, действующие на отдельные свободные тела, заменяя внутренние и внешние связи соответствующими реакциями (табл. 1.1).

3. Проверяем, удовлетворяет ли общее количество неизвестных S и количество уравнений равновесия l₁ + l₂ + … + l_n условию, которое отображает формула (5.11). Если да – задача статически определенная. Приступаем к её решению.

4. Составляем уравнения равновесия для каждого тела, начиная (если это возможно) с тела, для которого количество неизвестных не превышает количества уравнений равновесия.

5. Проверку рационально сделать для всей составной конструкции, считая, что гибкие связи и шарниры затвердели, то есть воспользоваться схемой сил, которую изобразили в первом пункте Плана.

Видео:Составная рама с распределенной нагрузкойСкачать

Расчет составной конструкции в теоретической механике

Расчет составной конструкции:

Постановка задачи. Плоская рама состоит из двух частей, соединенных одним шарниром. На раму действует момент и силы. Учитывая погонный вес, найти реакции опор.

Составная конструкция, состоящая из двух тел, соединенных шарниром содержит четыре неизвестные реакции опор. Так как для одного тела под действием плоской системы сил можно составить только три независимых уравнения равновесия, то для определения реакций необходимо рассматривать равновесие каждой части составной конструкции в отдельности.

1. Разбиваем систему на два тела по сочленяющему шарниру. В месте разбиения прикладываем реакции отброшенной части. Внешние связи заменяем их реакциями.

2. Для каждого тела, образованного при разбиении, составляем по три уравнения равновесия.

3. Решаем систему шести уравнений. Определяем реакции опор.

4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы.

2. Для каждого тела, образованного при разбиении, составляем уравнения моментов относительно точки сочленения. Полученные уравнения дополняем двумя уравнениями равновесия для всей конструкции в целом.

3. Решаем систему четырех уравнений. Определяем реакции опор.

4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы.

Задача №1

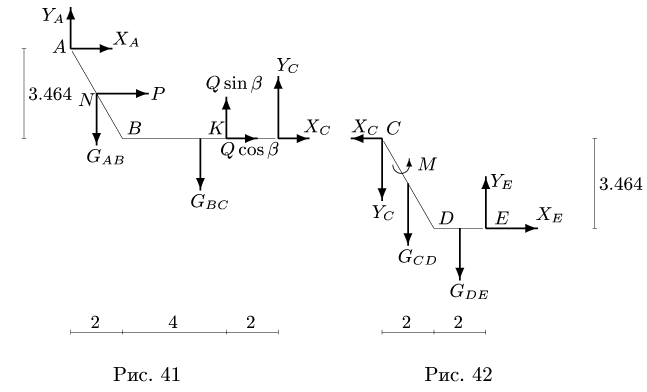
Плоская рама состоит из двух частей, соединенных в точке С шарниром. На раму действует момент М = 100 кНм, горизонтальная сила Р = 20 кН и наклонная сила Q = 10 кН. Учитывая погонный вес р = 4 кН/м, найти реакции опор (рис. 40). Дано:

2.4. Расчет составной конструкции

1. Разбиваем конструкцию на два тела по сочленяющему шарниру С. Получаем две части (рис. 41-42). Внешние связи конструкции заменяем реакциями.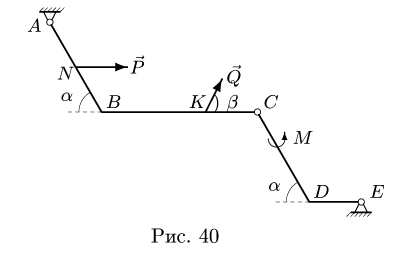

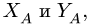
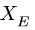
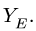
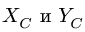
В точке А прикладываем реакции в точке Е — реакции и К каждому телу в точке С прикладываем реакции отброшенной части. Согласно 3-му закону Ньютона, реакции для разных частей равны по величине и направлены в противоположные стороны.

Система уравнений равновесия двух тел, образованных при разбиении, замыкается — имеем шесть уравнений равновесия (по три уравнения на каждую часть) и шесть неизвестных

2. Для каждой отдельной части составляем по три уравнения равновесия:

3. Решаем систему (1-6) относительно неизвестных 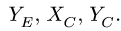Можно использовать любой способ решения системы линейных уравнений Рекомендуем наиболее эффективный для таких систем метод исключения Гаусса.

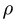
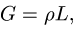
Если для решения использовать компьютер, систему лучше записать в матричном виде, предварительно вычислив правые части системы (1-6) и коэффициенты при неизвестных. Величины сил тяжести участков вычисляем через погонный вес по формуле где L — длина соответствующего участка. В нашем случае

Система (1-6) имеет следующий матричный вид:

2.4.Расчет составной конструкции

Результаты расчетов в кН заносим в таблицу:

4. Делаем проверку решения, составляя уравнения равновесия для целой (нерасчлененной) системы (рис. 43):

1. Разбиваем конструкцию на два тела по сочленяющему шарниру С. Получаем две части (рис. 41-42). Внешние связи конструкции заменяем реакциями.

2. Относительно шарнира С для каждой части конструкции составляем уравнения моментов (3) и (6). Для всей системы в целом составляем уравнения моментов (7,8) относительно опор А и Е.

3. Решаем систему четырех уравнений (3,6,7,8) относительно четырех неизвестных, замечая, что система распадается на две: уравнения (3) и (7) для 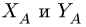и уравнения (6) и (8) для

4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы (рис. 43):

2.5. Конструкция с распределенными нагрузками

Видео:Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Конструкция с распределенными нагрузками

постановка задачи. Найти реакции опор плоской составной рамы, находящейся под действием линейно распределенной нагрузки и нагрузки, равномерно распределенной по дуге окружности.

1. Внешние связи заменяем реакциями. Разбиваем систему на два тела по сочленяющему шарниру. К каждой из образовавшихся частей прикладываем реакции шарнира, помня о том, что части взаимодействуют с силами равными по величине и противоположными по направлению.

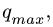
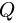
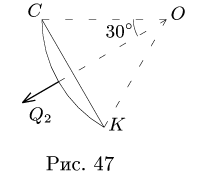
2. Линейную нагрузку с максимальным значением распределенную по треугольнику, заменяем на сосредоточенную в центре тяжести треугольника (1/3 длины участка L нагрузки, считая от прямого угла). Значение нагрузки вычисляем по формуле площади треугольника

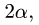
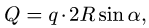
3. Нагрузку q, равномерно распределенную по дуге окружности радиусом R с центральным углом заменим ее равнодействующейнаправленной по биссектрисе центрального угла ([19], §21).

4. Для каждого тела составляем по три уравнения равновесия.

5. Решаем систему шести уравнений. Определяем реакции опор.

6. Делаем проверку решения, составляя уравнения равновесия для целой (нерасчлененной) системы.

Задача №2

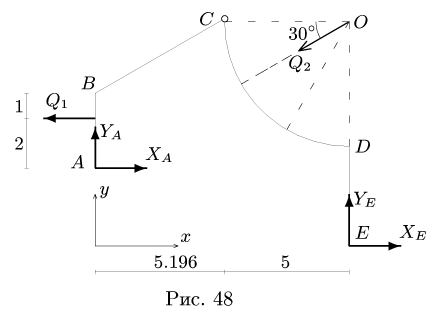
Найти реакции опор плоской составной рамы, находящейся под действием линейно распределенной нагрузки с максимальной интенсивностью на вертикальном участке рамы АВ

и нагрузки с интенсивностью равномерно распределенной по дуге СК окружности с центром в точке О (рис. 44). АВ = 3 м, ВС = 6 м, DE = 4 м, R = 5 м,

Решение

1. Внешние связи заменяем реакциями 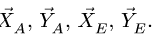Число неизвестных реакций больше трех. Следовательно, для решения задачи необходимо разбить конструкцию на две и рассмотреть равновесие каждой образовавшейся части(рис.45-46)

При разбиении по шарниру к каждой из частей прикладываем реакции шарнира, помня о том, что части взаимодействуют с силами, равными по величине и противоположными по направлению.

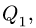
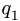
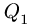
2. Нагрузку, распределенную по линейному закону, заменяем сосредоточенной приложенной к раме на расстоянии АВ/3 от максимального значения в том же направлении (рис. 45). Величина равнодействующей вычисляется по формуле площади прямоугольного треугольника с катетами

3. Нагрузку с интенсивностью 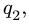равномерно распределенную по дуге СК, заменяем ее равнодействующей

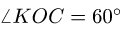
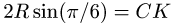
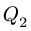
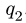
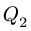
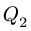
направленной по биссектрисе угла (рис. 47). Так как , то величина совпадает со значением равнодействующей нагрузки, равномерно распределенной по хорде СК, той же интенсивности . Воспользуемся тем, что вектор силы в теоретической механике является скользящим. Для удобства вычисления момента силы переносим точку ее приложения вдоль линии действия силы в центр окружности О. То, что точка О не принадлежит раме, и сила как-бы «зависает» в воздухе, не должно смущать. Твердое тело CDE можно мысленно расширить до точки О, давая, таким образом, силе реальную точку приложения.

4. Составляем уравнения равновесия частей рамы:

5. Решаем систему (1) шести уравнений с шестью неизвестными. Результаты расчетов в кН заносим в таблицу:

Гл.2.Произвольная плоская система сил

6. Выполняем проверку решения — составляем уравнения моментов для всей системы в целом (рис. 48):

Замечание. Можно предложить второй способ решения задачи, рассмотренный в предыдущем параграфе (с. 54). Для каждого тела, образованного при разбиении, составляем уравнения моментов относительно точки сочленения С. Полученные уравнения дополняем двумя уравнениями равновесия для всей конструкции в целом (рис. 48).

Для данного примера это уравнения моментов относительно опорных шарниров А и Е.

Расчет системы трех тел, соединенных шарниром

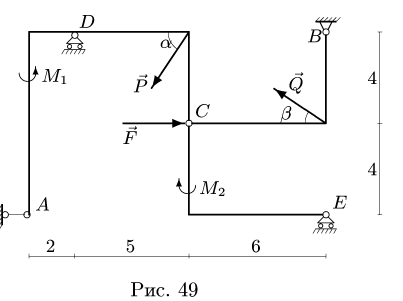
Постановка задачи. Определить реакции опор конструкции, состоящей из трех тел, соединенных в одной точке шарниром.

1. Расчленяем конструкцию на три отдельных тела и сочленяющий шарнир в качестве четвертого тела. Считая, что каждое из трех тел в точке сочленения взаимодействует только с осью шарнира, действие оси шарнира на тело заменяем ее реакциями.

2. Записываем по три уравнения равновесия для каждого из тел и два уравнения равновесия в проекциях для системы сил, приложенных к оси шарнира.

3. Решаем систему 11 уравнений с 11 неизвестными.

4. Выполняем проверку решения, составляя дополнительное уравнение равновесия для нерасчлененной конструкции.

Задача №3

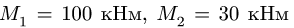
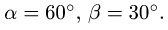
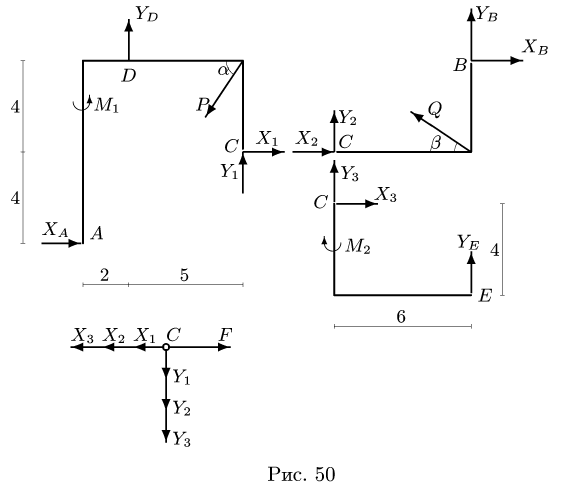
Определить реакции опор конструкции, состоящей из трех тел, соединенных в точке С шарниром. В точке В конструкция опирается на неподвижный шарнир, в точках D и Е — подвижные шарниры, в точке А — горизонтальный опорный стержень. На конструкцию действуют силы F — 40 кН, Р — 20 кН, Q — 10 кН и сосредоточенные моменты (рис. 49); Размеры на рисунке указаны в метрах.

1. Расчленяем конструкцию на три отдельных тела ADC, СВ, СЕ и сочленяющий шарнир С в качестве четвертого тела. Считая, что каждое из трех тел в точке сочленения взаимодействует только с осью шарнира С, действие оси шарнира на тело заменяем ее реакциями (рис. 50).

2. Для каждого из тел (АС, ВС, ЕС) записываем по три уравнения равновесия — два уравнения проекций и уравнение моментов относительно точки С 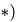. Для системы сил, сходящихся в шарнире С, составляем два уравнения равновесия в проекциях (рис. 50). Получаем следующую систему уравнений:

4. Решаем систему 11 уравнений с 11 неизвестными четов в кН записываем в таблицу:

5. Выполняем проверку решения, составляя дополнительное уравнение равновесия для нерасчлененной системы (рис. 51). Моментную точку К выбираем так, чтобы в уравнения вошли все проверяемые величины

В качестве моментной точки можно выбирать любую, в том числе и не принадлежащую телу.

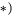
Замечание. Предложенный способ расчета не является единственным. Например, если из трех частей, соединенных в одном шарнире, можно отделить одну, имеющую в качестве опоры подвижный шарнир (часть СЕ, рис. 50), то получится система двух тел, одно из которых (СЕ) имеет три неизвестные реакции. Определить эти реакции можно из системы трех уравнений равновесия этой части.

Затем следует рассмотреть оставшуюся часть, состоящую их двух еще нерасчлененных тел. В качестве дополнительной нагрузки к ним будет приложены (в противоположную сторону) две реакции отброшенной третьей части.

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

Момент силы относительно оси
Равновесие вала
Определение усилий в стержнях, поддерживающих плиту
Тело на сферической и стержневых опорах
Определение передаточных отношений различных передач
Задачи на поступательное движение тела
Задачи на вращательное движение тела
Равновесие тяжелой рамы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.