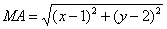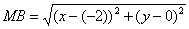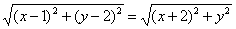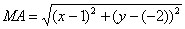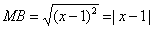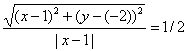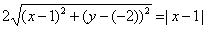Составить уравнение множества точек равноудаленных от двух параллельных плоскостей

Прямые y = -4x + 12 и y = -4x + 20 параллельны, т.к. их угловые коэффициенты равны.
Значит, точки, равноудаленные от этих прямых, лежат на прямой, параллельной данным.
Т.е. её уравнение будет выглядеть так: y = -4x + b.

Найдем точки пересечения функций с осью Ox: y = 0
для y = -4x + 12: x = 3
для y = -4x + 20: x = 5
Получаем (3; 0) и (5; 0).
Точка, которая лежит ровно между ними: (4; 0).
Точка (4; 0) принадлежит прямой y = -4x + b, значит, мы можем подставить её координаты в уравнение.
0 = -4*4 + b
b = 16

Таким образом, y = -4x + 16.

Если ответ по предмету Алгебра отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.

Множество точек на плоскости

Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как


то

После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.

Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /₂.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /₂. Так как:


то

или

Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.

Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.

Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.

Лекция 5. Метод геометрических множеств

Геометрическим множеством (ГМ) называется множество геометрических элементов (ГЭ), обладающих каким-либо общим геометрическим свойством.

5.1. Геометрические множества

Геометрические множества некоторых геометрических элементов

ГМ точек	ГМ прямых	ГМ плоскостей
1. Удаленных от заданной точки О на расстояние l
Сфера радиусом l с центром в точке О.	Совокупность прямых, касательных к сфере радиусом l с центром в точке О.	Совокупность плоскостей, касательных к сфере радиусом l с центром в точке О.
2. Удаленных от данной прямой m на расстояние l
Цилиндрическая поверхность радиусом l и осью m.	Совокупность прямых, касательных к поверхности цилиндра радиусом l и осью m, а также все образующие этой цилиндрической поверхности.	Совокупность плоскостей, касательных к поверхности цилиндра радиусом l и осью m.
3. Удаленных от данной плоскости σ на расстояние l
Две плоскости τ 1 и τ 2 //σ, расположенные по разные стороны от неё на расстоянии l
4. Равноудаленных от точек А и В
Все точки плоскости σ⊥АВ, проходящей через середину отрезка АВ.	Совокупность прямых, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.	Совокупность плоскостей, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.
5. Равноудаленных от двух параллельных прямых
Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему.	Совокупность прямых, лежащих в плоскости, проходящей через сере-дину отрезка (расстояния между данными прямыми) и перпендикулярной ему.	Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему, а также две плоскости, касательные к двум цилиндрическим поверхностям с осями – данными прямыми и равного диаметра.

5.2. Алгоритм решения задач методом геометрических множеств

1. 1. Условие задачи разбиваем на ряд простейших условий, каждому из которых должно отвечать определенное свойство искомого элемента (или элементов).

1. 1. Для каждого простейшего условия определяем удовлетворяющее ему геометрическое множество элементов.

1. 1. Находим общее решение задачи как некое геометрическое множество элементов, удовлетворяющих одновременно всем простейшим условиям. Оно представляет собой пересечение выбранных элементарных геометрических множеств.

1. Проводим анализ возможных решений, цель которого выявить когда, сколько и каких решений может быть в данной задаче в зависимости от взаимного положения заданных геометрических элементов, а, следовательно, связанных с ним геометрических множеств.

Упражнение

1. На заданной прямой m построить точку, удаленную от точки О на расстояние l (Рисунок 5.1).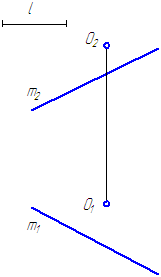

Рисунок 5.1
I. Геометрическое решение в пространстве

1. Искомые точки должны принадлежать прямой m, следовательно, решение по первому условию – любая точка на прямой.
2. Множество точек, удаленных от точки О на расстояние l образуют в пространстве сферу, с центром в точке О и радиусом равным l.
3. Общее решение задачи – точки, одновременно принадлежащие прямой m и сфере, то есть точки пересечения прямой m со сферой.

II. Графическое решение задачи (Рисунок 5.2).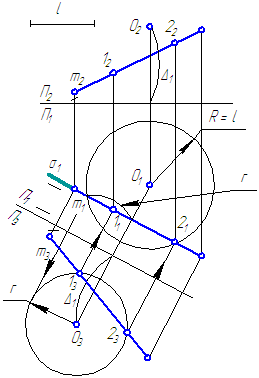

Рисунок 5.2
III. Анализ возможных решений (Рисунок 5.3).

Рисунок 5.3

Обозначим Δ – расстояние от точки О до прямой m:

• l > Δ – прямая пересечет сферу в двух точках;
• l = Δ – m – касательная к сфере → одна точка;
• l Краткая запись построения

1. 1. Строим проекцию сферы с центром в точке О и радиусом l.

1. 1. Через прямую m проводим секущую плоскость, например, σ⊥π₁. Плоскость σ пересекает сферу, в сечении – окружность.
   2. Вводим ДПП π₃⊥π₁ и π₃//σ.

1. Строим на π₃ проекции прямой m и окружности сечения, определяем точки пересечения прямой с окружностью, которые являются искомыми.

Упражнение

2. В плоскости σ=ΔАВС через точку А провести прямую AD, удаленную от точки О на расстояние l (О∈σ) (Рисунок 5.4). Геометрическое решение в пространстве

1. Прямая AD, удаленная от точки О на расстояние l, является касательной к сфере радиусом R_сф = l с центром в точке О.
2. Прямая AD∈σ.

Плоскость σ пересекает сферу по окружности.
Искомая прямая AD – касательная к окружности сечения плоскости σ и сферы.
II. Графическое решение задачи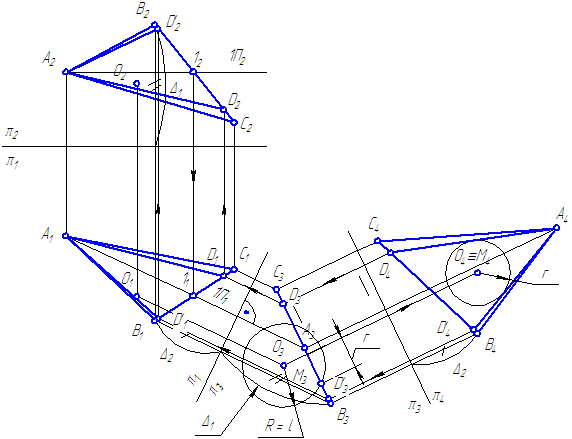

Рисунок 5.4
III. Анализ возможных решений
Обозначим Δ – расстояние от точки О до плоскости σ:

• l > Δ – плоскость пересечет сферу по окружности, → две прямые, проходящие через точку А и касательные к окружности сечения (если точка А вне окружности); если точка А на окружности сечения – одна прямая;если точка А внутри окружности сечения – решения нет;
• l = Δ – плоскость касается сферы → одна прямая, проходящая через точку А и точку касания; если точка А совпала с точкой касания → бесконечное множество прямых принадлежащих плоскости σ;
• l Краткая запись построения
  Находим истинную величину треугольника АВС, например, с помощью введения ДПП:

1. π₃⊥π₁ и π₃⊥σ.
2. π₄⊥π₃ и π₄//σ.
3. Строим окружность сечения σ со сферой. Строим касательные к этой окружности, проходящие через точку А.

5.3. Задачи для самостоятельной работы

1. Задана плоскость α=∆АВС и прямая m – общего положения. Определить угол между прямой m и плоскостью α. 2. Задана плоскость α=∆АВС и точка D вне плоскости. Повернуть точку D так, чтобы она совпала с плоскостью α. Ось вращения i⊥π₁.

🎦 Видео