С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
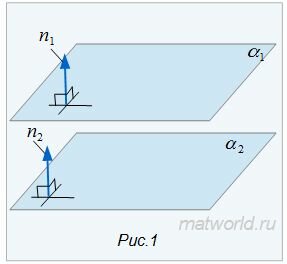 |
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
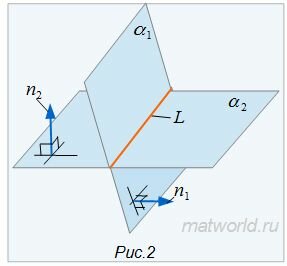 |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
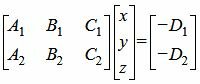 | (4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
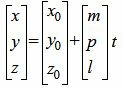 , , | (5) |
Равенство (5) можно записать в следующем виде:
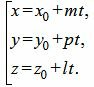 . . | (6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
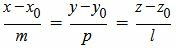 . . |
Пример 1. Найти линию пересечения плоскостей α1 и α2:
| α1: x+2y+z+54=0. | (7) |
| α2: 2x+9y−5z+32=0. | (8) |
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . . | (9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . . | (10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
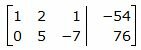 . . |
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
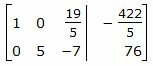 . . |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 . . |
 . . | (11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . . | (12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
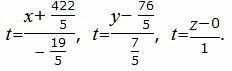 | (13) |
Из равентсв выше получим каноническое уравнение прямой:
 |
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
 |
Пример 2. Найти линию пересечения плоскостей α1 и α2:
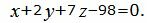 | (14) |
 | (15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
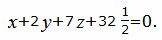 | (16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 | (17) |
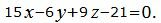 | (18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
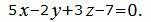 | (19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Составить уравнение линий пересечения конуса x2 y2 z2 0 с плоскостями y 3
1.Пример последовательности, у которой счётное множество предельных точек. Обосновать пример.
2.Составить уравнение прямой,образованной пересечением плоскости 3x-y-7z+9=0 с плоскотью,проходящей через ось Ox и точку E(3;2;-5).
3.Осевым сечением конусы является прямоугольный треугольник с катетом 32 см. Найдите объем конуса.
Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Составить уравнение линий пересечения конуса x2 y2 z2 0 с плоскостями y 3
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Пересечение поверхностей. Построение линии пересечения.Скачать

Где учитесь?
Для правильного составления решения, укажите:
Видео:Линия пересечения двух поверхностей конус и призма (Метод секущих плоскостей)Скачать

Задача 52584 составить уравнение плоскости.
Условие
составить уравнение плоскости, проходящей через линию пересечения двух сфер
2x^2+2y^2+2z^2+3x-2y+z-5=0
x^2+y^2+z^2-x+3y-2z+1=0
ответ: 5x-8y+5z-7=0
Решение
Находим точки пересечения сфер:
подставляем в первое:
Получаем множество точек(x;y;z), удовлетворяющих уравнению:
🎦 Видео
Пересечение конуса и сферы. Пошаговое видео. Инженерная графикаСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Поверхности второго порядкаСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)Скачать

Построение линии пересечения поверхностей методом СЕКУЩИХ ПЛОСКОСТЕЙСкачать

Задание 42. УСЕЧЕННЫЙ КОНУС. Часть 1Скачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Пересечение конуса и полусферыСкачать

Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Пересечение конуса и сферыСкачать

Пересечение конуса и призмыСкачать



