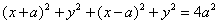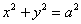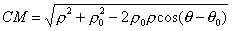Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Глава 10. Вывод уравнений заранее данных линий
В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера; в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.
ПРИМЕР 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек 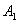
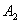
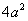
РЕШЕНИЕ. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М может занимать на линии любое положение то х и у являются переменными величинами; их называют текущими координатами.
Запишем геометрическое свойство линии символически:
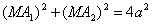
В этом отношении при движении точки М могут меняться длины 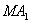
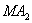
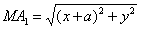
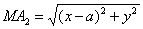
Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты х, у точки М:
Это и есть уравнение данной линии.
Действительно, для каждой точки М, лежающей на этой инии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).
Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде:
Теперь легко понять, что данная линия есть окружность с центром в начале координат и радиусом, равным а.
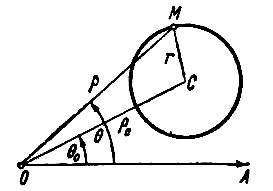
ПРИМЕР 2. В полярной системе координат вывести уравнение окружности, которая имеет центр С( 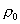
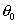
РЕШЕНИЕ. Олозначим буквой М произвольную точку окружности, буквами 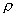
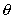
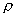
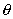
Все точки окружности отстоят от центра на расстоянии r ; запишем это условие символически:
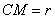
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов):
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты 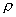
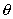
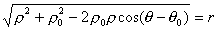
Это и есть уравнение данной окружности.
Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и , следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).
Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободным от радикала:
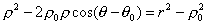
Видео:Задача на геометрическое место точек. Подготовка к зачету по геометрии 9 класс.Скачать

Найдите геометрическое место точек, сумма квадратов расстояний от каждой из которых до двух данных точек равна данному числу.
Пусть A и B — данные точки и AB = 2a, M — точка, для которой MA 2 + MB 2 = 2c 2 — данное число. Выберем на плоскости систему координат следующим образом. Начало координат — середина O отрезка AB, ось OX содержит отрезок OB, ось OY перпендикулярна ему. Выпишем координаты данных точек:A(- a;0) и B(a;0).
Для того, чтобы точка M(x;y) принадлежала искомому геометрическому месту точек, необходимо и достаточно, чтобы
После упрощения получим уравнение x 2 + y 2 = c 2 — a 2 .
Если c > a, то имеем окружность с центром в точке O и радиусом 
Пусть A и B — данные точки и AB = 2a, M — точка, для которой MA 2 + MB 2 = 2c 2 — данное число. Выберем на плоскости систему координат следующим образом. Начало координат — середина O отрезка AB, ось OX содержит отрезок OB, ось OY перпендикулярна ему. Выпишем координаты данных точек:A(- a;0) и B(a;0).
Для того, чтобы точка M(x;y) принадлежала искомому геометрическому месту точек, необходимо и достаточно, чтобы
После упрощения получим уравнение x 2 + y 2 = c 2 — a 2 .
Если c > a, то имеем окружность с центром в точке O и радиусом 
Пусть A и B — данные точки и AB = 2a, M — точка, для которой MA 2 + MB 2 = 2c 2 — данное число. Выберем на плоскости систему координат следующим образом. Начало координат — середина O отрезка AB, ось OX содержит отрезок OB, ось OY перпендикулярна ему. Выпишем координаты данных точек:A(- a;0) и B(a;0).
Для того, чтобы точка M(x;y) принадлежала искомому геометрическому месту точек, необходимо и достаточно, чтобы
После упрощения получим уравнение x 2 + y 2 = c 2 — a 2 .
Если c > a, то имеем окружность с центром в точке O и радиусом 

Ответ
Видео:PRO геометрические места точекСкачать

Задача 43842 Составить уравнение множества точек, для.
Условие
Составить уравнение множества точек, для каждой из которых выполняется следующее условие: сумма квадратов расстояний до точек A(1,1) и B (-3,3) равна 20
Все решения
Упрощаем, раскрываем скобки:
Выделим полные квадраты:
(x+1)^2+(y-2)^2=5 — уравнение окружности с центром в точке (-1;2)
R=sqrt(5)
💥 Видео
Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Метод выделения полного квадрата. 8 класс.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

#67. Сумма квадратов корней в уравнении с параметром!Скачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Уравнения стороны треугольника и медианыСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Длина отрезкаСкачать

Уравнение окружности (1)Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика| Разложение квадратного трехчлена на множители.Скачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Метод наименьших квадратов. ТемаСкачать

47. ГМТ ЭллипсСкачать