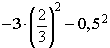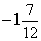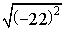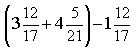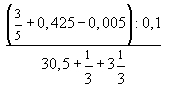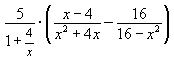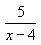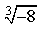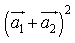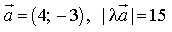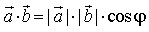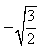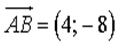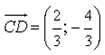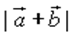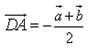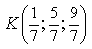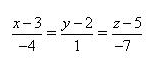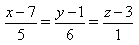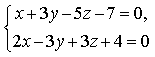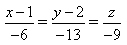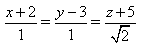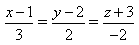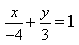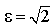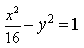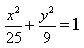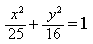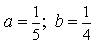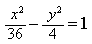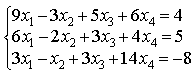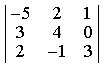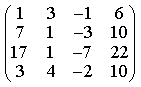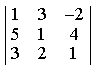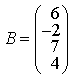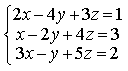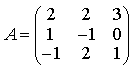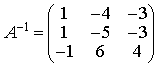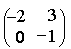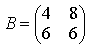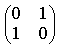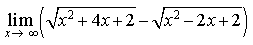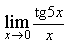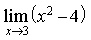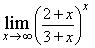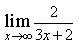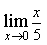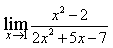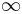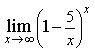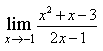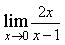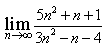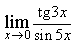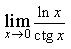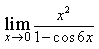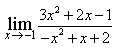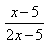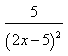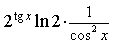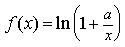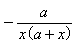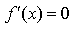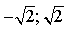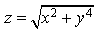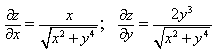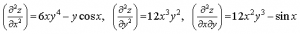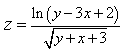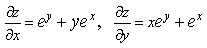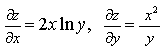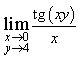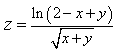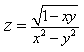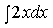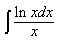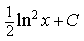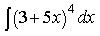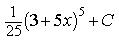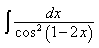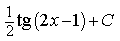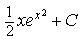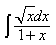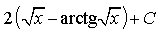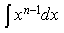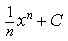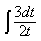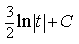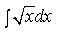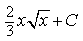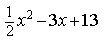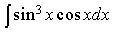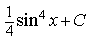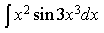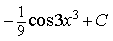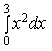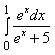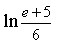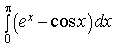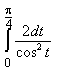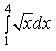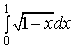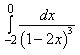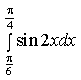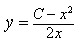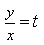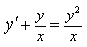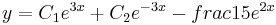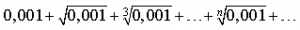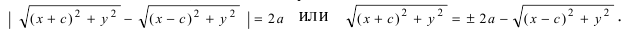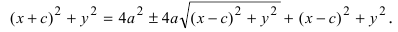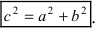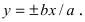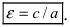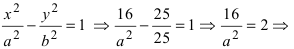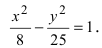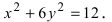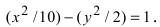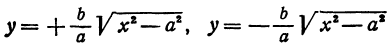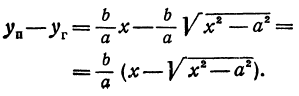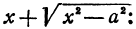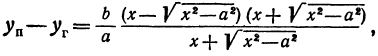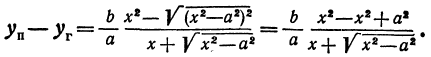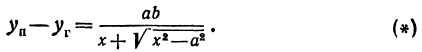- Определение гиперболы, решаем задачи вместе
- Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
- Ответы на все модули (для контрольного теста) по предмету математика
- Гипербола — определение и вычисление с примерами решения
- Гипербола в высшей математике
- Составить каноническое уравнение гиперболы фокусы которой лежат на оси oy
- 📺 Видео
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.
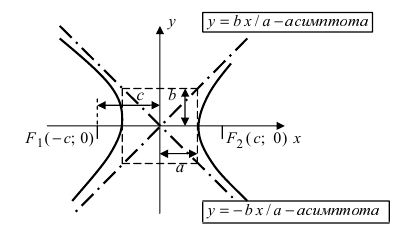
На чертеже ниже фокусы обозначены как 

На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:
Если 




Если 




На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Видео:Фокусы гиперболыСкачать

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Ответы на все модули (для контрольного теста) по предмету математика
Ответы на все модули (для контрольного теста) по предмету математика.
Ответы на модуль 1 (ЧИСЛА) по предмету математика.
1) Найдите значение выражения
2) Упростите иррациональное выражение
22
10000
6) Какое из перечисленных чисел является иррациональным?
3,141592…
7) Вычислите
6*5/21
8) Какая из перечисленных дробей является смешанной периодической дробью?
2,75(12)
9) Вычислите с точностью до десятых
0,3
10) Найдите значение выражения 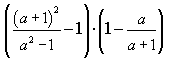
2/3
11) Упростите
12) Найдите
-2
13) Какие числа называются целыми?
натуральные числа, числа противоположные натуральным, и число 0
Ответы на модуль 2 (ВЕКТОРНАЯ АЛГЕБРА) по предмету математика.
1) Дано: 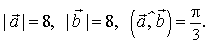
32
2) Дано: 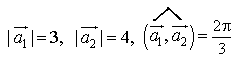
13
3) Найдите l , если
3 или -3
4) Что называется скалярным произведением двух векторов?
число, определяемое по формуле
5) Найдите l , если
2,5 или -2,5
6) Даны векторы 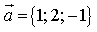

7) Даны точки M(-5; 7; -6), N(7; -9; 9). Вычислите проекцию вектора 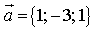
3
8) При каком значении l векторы MP и KD коллинеарны, если M(-3; 2), P(-1; -2), K(2; 1), D(5;l)?
-5
9) Какие векторы называются коллинеарными?
лежащие на одной прямой или параллельных прямых
10) Векторы называются компланарными, если
они лежат в одной плоскости или параллельных плоскостях
11) Какой из перечисленных векторов коллинеарен вектору
12) Векторы a и b взаимно перпендикулярны (ортогональны), причем |a|=5 и |b|=12 . Определите
13
13) Векторы AC=a и BD=d служат диагоналями параллелограмма ABCD. Выразите вектор DA через векторы a и b
Ответы на модуль 3 (АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ) по предмету математика.
1) Найдите координаты точки K пересечения прямой 
2) Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M1(-2; 3)
5x+ 13y— 29 = 0
3) Укажите канонические уравнения прямой, проходящей через точки M1(3; 2; 5) и M2(-1; 3; -2)
4) Даны прямые 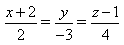
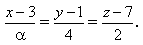
a= 2
5) Установите взаимное расположение прямых 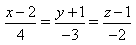
прямые перпендикулярны
6) Укажите канонические уравнения прямой
7) Найдите острый угол между прямыми 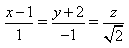
60°
8) Составьте уравнение плоскости, проходящей через параллельные прямые 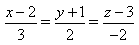
9) Даны вершины треугольника ABC: A(3; -1),B(4; 2) и C(-2; 0). Напишите уравнения его сторон
10) Уравнение 3x— 4y+ 12 = 0 преобразуйте к уравнению в отрезках
11) Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол j= 45°
12) Найдите координаты точки пересечения прямых 2x—y— 3 = 0 и 4x+ 3y— 11 = 0
(2; 1)
13) Найдите уравнение прямой, проходящей через точки M1(3; 2), M2(4;-1)
Ответы на модуль 4 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.
1) Определите эксцентриситет равносторонней гиперболы
2) Укажите уравнение окружности, которая проходит через точки А(3;1) и В(-1; 3), а ее центр лежит на прямой 3x—y— 2 = 0
(x— 2) 2 + (y— 4) 2 = 10
3) Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5)
(x— 2) 2 + (y+ 5) 2 = 8 2
4) Определите полуоси гиперболы
5) Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x— 4y+ 20 = 0 является касательной к окружности
x 2 +y 2 = 16
6) Укажите уравнение окружности, которая проходит через точку А(2;6) и ее центр совпадает с точкой C(-1; 2)
(x+ 1) 2 + (y— 2) 2 = 25
7) Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b= 3
8) Напишите уравнение эллипса, если даны его полуоси a= 5 и b= 4
9) Укажите уравнение окружности, проходящей через точку (4; 5) с центром в точке (1; -3)
(x— 1) 2 + (y+ 3) 2 = 73
10) Определите полуоси гиперболы 25x 2 — 16y 2 =1
11) Напишите уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a= 6 и b= 2
12) Укажите уравнение параболы, с вершиной в точке O и фокусом F(4; 0)
13) Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров
(x— 1) 2 + (y— 4) 2 = 8
Ответы на модуль 5 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.
1) Найдите общее решение системы
2) Вычислите определитель
-89
3) Найдите ранг и базисные строки матрицы
2. 1-я строка, 2-я строка
4) Вычислите определитель
0
5) Найдите А × В, где 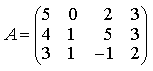
6) Решите систему уравнений методом Крамера
7) Найдите обратную матрицу для матрицы
8) Найдите ранг матрицы
4
9) Определитель системы трех линейных уравнений с тремя неизвестными равен 5. Это означает, что
система имеет единственное решений
11) Метод Гаусса решения системы линейных уравнений предполагает использование
последовательного исключения неизвестных
12) Система линейных уравнений называется совместной, если
она имеет хотя бы одно решение
13) Решите матричное уравнение AX + AXA = B, где 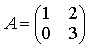
Ответы на модуль 6 (МАТЕМАТИЧЕСКИЙ АНАЛИЗ) по предмету математика.
1) Найдите предел
3
2) Найдите предел
5
3) Найдите предел
5
4) Найдите предел
1/e
5) Найдите предел
0
6) Найдите предел
0
7) Найдите предел
8) Найдите предел
1/2
9) Найдите предел
e — 5
10) Найдите предел
1
11) Найдите предел
0
12) Найдите предел
5/3
13) Найдите предел
3/5
Ответы на модуль 7 (ДИФФЕРЕНЦИРОВАНИЕ) по предмету математика.
1) Вычислите предел по правилу Лопиталя
0
2) Найдите производную функции f(x)=(1+ cos x)sin x
cos x+ cos 2x
3) Вычислите предел по правилу Лопиталя
1/18
4) Вычислите предел по правилу Лопиталя
-4/3
5) Найдите производную функции y= sin(2x 2 + 3)
4xcos(2x 2 + 3)
6) Найдите производную функции y=(3e x +x)× cos x
(3e x + 1) × cos x— (3e x +x) × sin x
7) Для функции 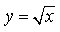
1/14
8) Найдите производную функции
9) Найдите производную функции y=2 tg x
10) Найдите производную функции
11) Найдите скорость тела, движущего по закону S=3t-5
3
12) Дана функция 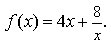
13) Найдите производную функции y=xe x —e x
xe x
Ответы на модуль 8 (ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ) по предмету математика.
1) Число f(x0) называется наибольшим значением функции на отрезке [a;b], если
для всех x из этого отрезка выполняется неравенство f(x) 2 — 3x+ 1
убывает при x 3/2
3) Найдите точки максимума (минимума) функции y=- 5x 2 — 2x+ 2
(-0,2;2,2) точка максимума
4) Каково необходимое условие возрастания функции?
если функция y=f(x) дифференцируема и возрастает на интервале (a;b), то f(x)>=0 для всех xиз этого интервала
5) Определите поведение функции y= 2x 2 при x= 1
возрастает
6) В каких точках выпукла или вогнута кривая y=x 2 — 3x+ 6
вогнута во всех точках
7) Найдите промежутки возрастания или убывания функции y=- 2x 2 + 8x— 1
(0; 0)
9) Найдите точки перегиба кривой y=x 4 — 12x 3 + 48x 2 — 50
(2; 62) и (4; 206)
10) Найдите точки максимума (минимума) функции y=x 2 — 2x
(1;-1) точка минимума
11) Вертикальные асимптоты к графику функции 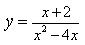
12) Найдите наибольшее и наименьшее значения функции y=x 2 на промежутке [-1; 3]
13) В каких точках выпукла или вогнута кривая y= 2 — 3x—x 2
выпукла во всех точках
Ответы на модуль 9 (ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ) по предмету математика.
1) Найдите частные производные функции двух переменных
2) Найдите частные производные второго порядка функции z=x 3 y 4 +ycos x
3) Найдите предел функции 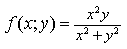
0
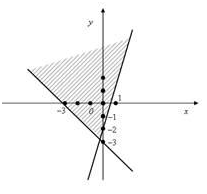
4) На каком из рисунков изображена область определения функции
5) Найдите частные производные функции двух переменных z=xe y +ye x
6) Найдите частные производные функции z=x 2 × ln y
7) Найдите полный дифференциал функции z=x 2 y+xy 2
8) Какая поверхность называется графиком функции n переменных?
9) Укажите полное приращение функции f(x;y)
10) Найдите
4
11) Укажите частное приращение функции f(x;y)по переменной у
12) На каком из рисунков изображена область определения функции
13) Найдите область определения функции
xy 2 не =y 2
Ответы на модуль 10 (НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ) по предмету математика.
1) Найдите
2) Найдите
3) Найдите
4) Найдите
5) Найдите
6) Найдите
7) Найдите
8) Найдите
9) Найдите
10) Найдите 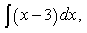
11) Найдите
12) Найдите 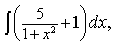
13) Найдите
Ответы на модуль 11 (ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ) по предмету математика.
1) Скорость точки, движущейся прямолинейно, задана уравнением v=9t 2 -2t-8. Вычислите путь, пройденный точкой за 3 с от начала движения
48 м
2) Вычислите определенный интеграл
9
3) Сила в 6 кГ растягивает пружину на 8 см. Какую работу она производит?
0,24 кГм
4) Вычислите определенный интеграл
5) Вычислите определенный интеграл
e p -1
6) Найдите площадь фигуры, заключенной между прямыми y=4x— 5, x=-3, x=-2 и осью Ox
15
7) Скорость падающего в пустоте тела определяется по формуле v= 9,8t м/сек. Какой путь пройдет тело за первые 10 секунд падения?
490 м
8) Найдите площадь фигуры, ограниченной прямыми y=5x, x=2 и осью Ox
10
9) Вычислите определенный интеграл
2
10) Вычислите определенный интеграл
4*2/3
11) Вычислите определенный интеграл
2/3
12) Вычислите определенный интеграл
0,24
13) Вычислите определенный интеграл
0,25
Ответы на модуль 12 (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ) по предмету математика.
1) Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?
частным решением
2) Найдите общее решение уравнения (x+y)dx+xdy=0
3) При решении каких уравнений используют подстановку
при решении однородных уравнений
4) Найдите общее решение уравнения xy 2 dy=(x 3 +y 3 )dx
5) Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли
6) Найдите общее решение уравнения y — 9y = e 2 x
7) Найдите общее решение уравнения
8) Найдите частное решение уравнения ds=(4t-3)dt, если при t= 0 s= 0
9) Найдите общее решение уравнения y—y= 0
10) Найдите общее решение уравнения
11) Среди перечисленных дифференциальных уравнений укажите однородное уравнение
12) Найдите общее решение уравнения y— 4y+ 3y= 0
13) Найдите общее решение уравнения y = cos x
Ответы на модуль 13 (РЯДЫ) по предмету математика.
1) Исследуйте сходимость ряда
сходится
2) Найдите интервал сходимости ряда x+2x 2 +3x 3 +4x 4 +…+nx n +…, не исследуя концов интервала
(-1; 1)
3) Найдите радиус сходимости ряда
4) Разложите в степенной ряд f(x)= arctg 3x
5) Исследуйте сходимость ряда
расходится
6) Исследуйте сходимость ряда
сходится
7) Найдите интервал сходимости ряда
8) Исследуйте сходимость ряда
расходится
9) Исследуйте сходимость ряда
расходится
10) Исследуйте сходимость ряда
сходится
11) Разложите в степенной ряд f(x)= sin 2x
12) Исследуйте сходимость ряда
расходится
13) Исследуйте сходимость ряда
сходится
Ответы на задачник по предмету математика.
1) Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
x — y + 3z — 11 = 0
2) Вычислить определитель D, разложив его по элементам второго столбца.
-20
3) Вычислить J= ∫cos(lnx) dx/x
sin(lnx)+ C
4) Найти lim x—>0 (5 x — cos x)
0
5) Вычислить площадь фигуры, ограниченной линиями 4y = x 2 , y 2 = 4x.
16/3
6) Найти производную функции y =ln sinx
ctg x
7) Найдите угол между векторами a = 2m+4n и b = m-n, где m и n — единичные векторы и угол между m и n равен 120 о
120
8) Найти наименьшее значение функции y = x 2 – 6x + 5 на отрезке (1,2).
-3
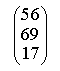
X1=2, X2=3, X3=-2.
10) При каком положительном значении параметра t прямые, заданные уравнениями
3tx — 8y + 1 = 0 и (1+t)x — 2ty = 0, параллельны?
Видео:§23 Построение гиперболыСкачать

Гипербола — определение и вычисление с примерами решения
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 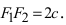
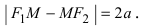
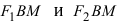
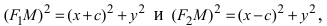
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 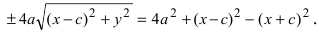
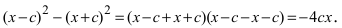
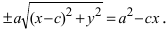
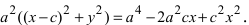
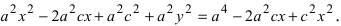
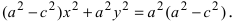
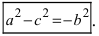
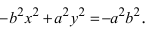
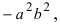
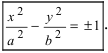
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 
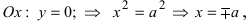
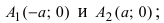
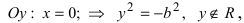
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 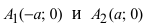
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 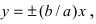
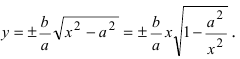
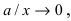
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 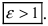
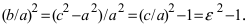
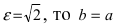
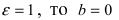
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
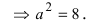
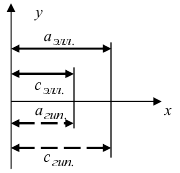
Пример:
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 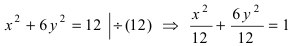
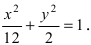
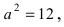
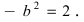
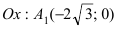
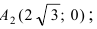
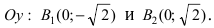
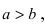
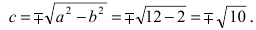
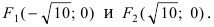
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 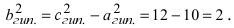
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Гипербола в высшей математике
Решая его относительно 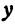
или одну двузначную функцию
Функция 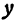

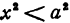
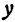
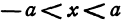
При 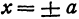
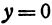
При 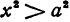
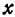
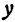
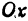
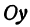
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
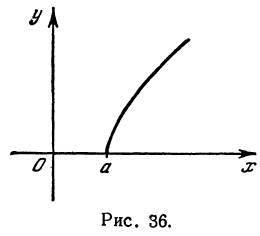
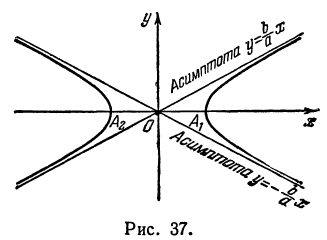
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 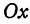
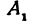
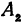
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 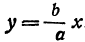
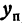
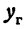
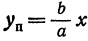
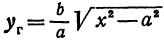
Умножим и разделим правую часть на
Будем придавать 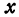
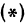

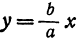
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 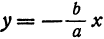
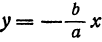
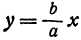
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:§21 Каноническое уравнение гиперболыСкачать

Составить каноническое уравнение гиперболы фокусы которой лежат на оси oy
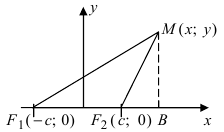
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, равная 2 a .
Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2 c , а сумму расстояний от произвольной точки эллипса до фокусов – через 2 a . По определению 2 a > 2 c , то есть a > c .
Выберем систему координат так, чтобы фокусы F 1 и F 2 лежали на оси 0 x , а начало координат совпадало с серединой отрезка F 1 F 2 . Тогда фокусы имют координаты: F 1 (– c ;0) и F 2 ( c ;0) . Пусть M ( x ; y ) – произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Это уравнение равносильно первоначальному. Оно называется каноническим уравнением эллипса – кривой второго порядка .
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (2.17) содержит x и y только в четных степенях, поэтому если точка ( x ; y ) принадлежит эллипсу, то ему также принадлежат точки (– x ; y ), ( x ;– y ), (– x ;– y ) . Отсюда: эллипс симметричен относительно осей 0 x и 0 y , а также относительно точки O (0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив y = 0, найдем точки A 1 ( a ; 0) и A 2 (– a ; 0), в которых ось 0 x пересекает эллипс. Положив в уравнении (2.17) x = 0, находим точки пересечения эллипса с осью 0 y : B 1 (0; b ) и B 2 (0;– b ). Точки A 1 , A 2 , B 1 , B 2 называются вершинами эллипса. Отрезки А1А2, В1В2, а также их длины 2 a и 2 b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в левой части не превосходит единицы, т.е.:
Следовательно, все точки эллипса лежат внутри прямоугольника, ограниченного прямыми x = ± a и y = ± b .
4. В уравнении (2.17) левая часть – сумма неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет уменьшаться, если | x | возрастает, | y | уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму овальной замкнутой кривой. Форма эллипса зависит от отношения 


Отсюда видно, что чем меньше эксцентриситет эллипса, тем будет менее эллипс сплющенным; при ε = 0 эллипс превращается в окружность.
Прямые 
Если r – расстояние от произвольной точки до какого–нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение 

Из равенства a 2 – c 2 = b 2 следует, что a > b . Если же наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2 b лежит на оси 0 y , а малая ось 2 a – на оси 0 x . Фокусы такого эллипса находятся в точках F 1 (0; c ) и F 2 (0;– c ) , где 
Пример 2.5. Составить уравнение линии, для каждой точки которой отношение расстояний от нее до точки A (3;0) и до прямой x = 12, равно числу ε =0,5 . Полученное уравнение привести к простейшему виду .
Решение . Пусть M ( x ; y ) – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр MB на прямую . Тогда точка B( 12;y) . По условию задачи 
По формуле расстояния 
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения (сферой) 
Пример 2.6. В геодезии используется система географических координат, основанная на понятии геоида. Геоид – поверхность Земли, ограниченная уровенной поверхностью, продолженной под континенты. Поверхность геоида отличается от физической поверхности Земли, на которой резко выражены горы и океанические впадины.
Тело, поверхность которого более всего соответствует поверхности геоида, имеет определенные размеры и ориентирована соответственно в теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех геодезических работ принят референц–эллипсоид Красовского с параметрами a = 6 378 245 м, b = 6 356 863 м, α = 1: 298,3.
Линия, проходящая вертикально через центр эллипсоида является полярной осью. Линия, проходящая через центр эллипсоида, перпендикулярно к полярной оси, – экваториальной осью. При пересечении поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно к полярной оси, образуется окружность, называемая экватором. Окружность, полученная от пересечения поверхности эллипсоида плоскостью, параллельной плоскости экватора, называется параллелью. Линия пересечения поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную ось, называется меридианом данной точки. Положение точки на земной поверхности определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной линией называется географической широтой. Для определения долгот точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол λ, составленный плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана, называется географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости – фокусов, есть величина постоянная, равная 2 a .
Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2 c , а модуль разности расстояний от каждой точки гиперболы до фокусов через 2 a . По определению 2 a 2 c , то есть a c .
Выберем систему координат x 0 y так, чтобы фокусы F 1 и F 2 лежали на оси 0 x , а начало координат совпало с серединой отрезка F 1 F 2 . Тогда фокусы будут иметь координаты F 1( c ;0 ) и F 2 (– c ;0 ). На этой основе выведем уравнение гиперболы. Пусть M ( x ; y ) – ее произвольная точка . Тогда по определению | MF 1 – MF 2 |= 2 a , то есть 
где b 2 = a 2 – c 2 . Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического уравнения.
1. Уравнение (2.18) содержит x и y только в четных степенях. Следовательно, гипербола симметрична относительно осей координат 0 x и 0 y , и относительно точки O (0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (2.18) y =0 , находим две точки пересечения гиперболы с осью 0 x : A 1 ( a ; 0) и A 2 (– a ; 0).
Положив в (2.18) x = 0, получаем y 2 = – b 2 , чего быть не может. Т.е. гипербола ось 0 y не пересекает.
3. Из уравнения (2.18) следует, что уменьшаемое 
4. Из уравнения (2.18) гиперболы видно, что когда | x | возрастает, то | y | также возрастает . Это следует из того, что разность 
Прямая L называется асимптотой некоторой неограниченной кривой , если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном удалении т очки M вдоль кривой от начала координат.
Покажем, что гипербола 

Возьмем на прямой 

Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка | MN | стремится к нулю. Так как | MN | больше расстояния d от точки M до прямой L, то d стремится к нулю тем более ( и подавно) . Следовательно, прямые 
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы .
Эксцентриситет гиперболы – отношение расстояния между фокусами к величине её действительной оси, обозначается ε : 


Эксцентриситет равносторонней гиперболы равен 

Прямые 


Уравнение 
Значит , гиперболы 
Примечание. Если у кривой 2–го порядка смещен центр в некоторую точку O ’ ( x 0 ; y 0 ) , то она называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме: «Исследование общего уравнения 2–ой степени» (смотри схему 10), частными случаями которого являются данные формулы.
📺 Видео
§31.1 Приведение уравнения кривой к каноническому видуСкачать

Видеоурок "Гипербола"Скачать

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертежСкачать

Эту задачу ГРИГОРИЙ ПЕРЕЛЬМАН решил в 10-м классеСкачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

213. Фокус и директриса параболы.Скачать

165. Найти фокусы и эксцентриситет эллипса.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

§29 Эксцентриситет гиперболыСкачать

§18 Каноническое уравнение эллипсаСкачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать