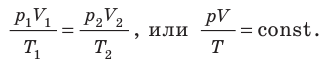Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.
ν — количество вещества [моль]
R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]
T – температура [K]
Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.
- Вывод уравнения Менделеева-Клапейрона
- Закон Бойля-Мариотта — изотермический процесс
- Закон Гей-Люссака — изобарный процесс
- Закон Шарля — изобарный процесс
- Законы идеального газа
- Конспект лекции с демонстрациями
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- 📺 Видео
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Вывод уравнения Менделеева-Клапейрона
Давление идеального газа зависит от концентрации частиц и температуры тела:
n — концентрация частиц [м -3 ]
k – константа Больцмана k = 1,38 · 10 -23 [Дж/К]
Т – абсолютная температура, в кельвинах [К]
Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:
Подставим nkT вместо давления и выразим кинетическую энергию:
Концентрация частиц газа n равна:
N – число молекул газа в емкости объемом V [м 3 ]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:
Подставим эти величины в уравнение давления идеального газа (p=nkT):
Произведение числа Авогадро NA и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:
Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:
можно привести уравнение к следующему виду:
Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.
Закон Бойля-Мариотта — изотермический процесс
Проходит при постоянной температуре: T= const.
P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:
Закон Гей-Люссака — изобарный процесс
Проходит при постоянном давлении: P = const.
V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:
Закон Шарля — изобарный процесс
Проходит при постоянном объеме: V = const.
P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:
Понравилась статья, расскажите о ней друзьям:
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Законы идеального газа
Конспект лекции с демонстрациями
Аннотация: традиционное изложение темы, дополненное демонстрацией на компьютерной модели.
Из трех агрегатных состояний вещества наиболее простым является газообразное состояние. В газах силы, действующие между молекулами, малы и при определенных условиях ими можно пренебречь.
Газ называется идеальным, если:
— можно пренебречь размерами молекул, т.е. можно считать молекулы материальными точками;
— можно пренебречь силами взаимодействия между молекулами (потенциальная энергия взаимодействия молекул много меньше их кинетической энергии);
— удары молекул друг с другом и со стенками сосуда можно считать абсолютно упругими.
Реальные газы близки по свойствам к идеальному при:
— условиях, близких к нормальным условиям (t = 0 0 C, p = 1.013·10 5 Па);
— при высоких температурах.
Законы, которым подчиняется поведение идеальных газов, были открыты опытным путем достаточно давно. Так, закон Бойля — Мариотта установлен еще в 17 веке. Дадим формулировки этих законов.
Закон Бойля — Мариотта. Пусть газ находится в условиях, когда его температура поддерживается постоянной (такие условия называются изотермическими).Тогда для данной массы газа произведение давления на объем есть величина постоянная:
Эту формулу называют уравнением изотермы. Графически зависимость p от V для различных температур изображена на рисунке.
Свойство тела изменять давление при изменении объема называется сжимаемостью. Если изменение объема происходит при T=const, то сжимаемость характеризуется изотермическим коэффициентом сжимаемости 
Для идеального газа легко вычислить его значение. Из уравнения изотермы получаем:
Знак минус указывает на то, что при увеличении объема давление уменьшается. Т.о., изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления. С ростом давления он уменьшается, т.к. чем больше давление, тем меньше у газа возможностей для дальнейшего сжатия.
Закон Гей — Люссака. Пусть газ находится в условиях, когда постоянным поддерживается его давление (такие условия называются изобарическими). Их можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем. Тогда изменение температуры газа приведет к перемещению поршня и изменению объема. Давление же газа останется постоянным. При этом для данной массы газа его объем будет пропорционален температуре:
где V0 — объем при температуре t = 0 0 C, 
Графически зависимость V от T для различных давлений изображена на рисунке.
Перейдя от температуры в шкале Цельсия к абсолютной температуре 
Закон Шарля. Если газ находится в условиях, когда постоянным остается его объем (изохорические условия), то для данной массы газа давление будет пропорционально температуре:
где р0 — давление при температуре t = 0 0 C, 
Закон Шарля также можно записать в виде:
Закон Авогадро: один моль любого идеального газа при одинаковых температуре и давлении занимает одинаковый объем. При нормальных условиях (t = 0 0 C, p = 1.03·10 5 Па) этот объем равен 
Число частиц, содержащихся в 1 моле различных веществ, наз. постоянная Авогадро:
Легко вычислить и число n0 частиц в 1 м 3 при нормальных условиях:
Это число называется числом Лошмидта.
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов, т.е.
где 
Уравнение Клапейрона — Менделеева. Из законов идеального газа можно получить уравнение состояния, связывающее Т, р и V идеального газа в состоянии равновесия. Это уравнение впервые было получено французским физиком и инженером Б. Клапейроном и российским учеными Д.И. Менделеевым, поэтому носит их имя.
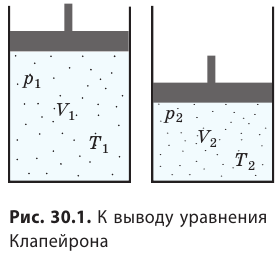
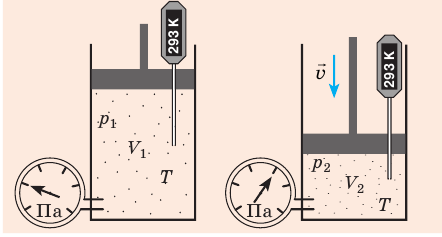
Пусть некоторая масса газа занимает объем V1, имеет давление p1 и находится при температуре Т1. Эта же масса газа в другом состоянии характеризуется параметрами V2, p2, Т2 (см. рисунок). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: изотермического (1 — 1′) и изохорического (1′ — 2).
Для данных процессов можно записать законы Бойля — Мариотта и Гей — Люссака:
Исключив из уравнений p1 ‘ , получим
Так как состояния 1 и 2 были выбраны произвольно, то последнее уравнение можно записать в виде:
Это уравнение называется уравнением Клапейрона, в котором В — постоянная, различная для различных масс газов.
Менделеев объединил уравнение Клапейрона с законом Авогадро. Согласно закону Авогадро, 1 моль любого идеального газа при одинаковых p и T занимает один и тот же объем Vm, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется универсальной газовой постоянной. Тогда
Это уравнение и является уравнением состояния идеального газа, которое также носит название уравнение Клапейрона — Менделеева.
Числовое значение универсальной газовой постоянной можно определить, подставив в уравнение Клапейрона — Менделеева значения p, T и Vm при нормальных условиях:
Уравнение Клапейрона — Менделеева можно записать для любой массы газа. Для этого вспомним, что объем газа массы m связан с объемом одного моля формулой V=(m/M)Vm, где М — молярная масса газа. Тогда уравнение Клапейрона — Менделеева для газа массой m будет иметь вид:
где 
Часто уравнение состояния идеального газа записывают через постоянную Больцмана:
Исходя из этого, уравнение состояния можно представить как
где 
Небольшая демонстрация законов идеального газа. После нажатие кнопки «Начнем» Вы увидите комментарии ведущего к происходящему на экране (черный цвет) и описание действий компьютера после нажатия Вами кнопки «Далее» (коричневый цвет). Когда компьютер «занят» (т.е. идет опыт) эта кнопка не активна. Переходите к следующему кадру, лишь осмыслив результат, полученный в текущем опыте. (Если Ваше восприятие не совпадает с комментариями ведущего, напишите!)
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Уравнение состояния идеального газаСкачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 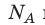
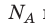
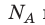
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (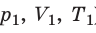
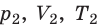
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 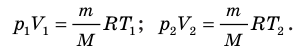
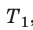
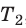
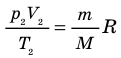
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (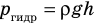
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (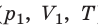
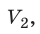
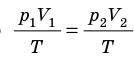
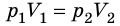
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 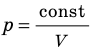
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (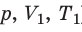
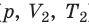
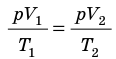
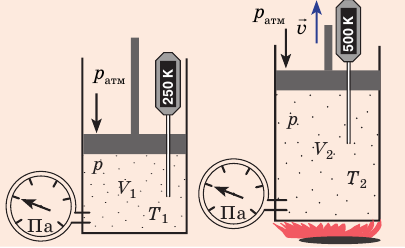
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
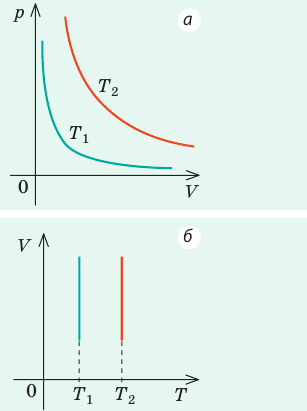
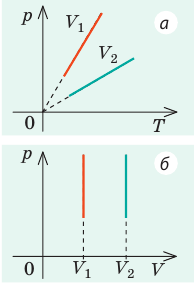
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (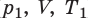
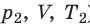
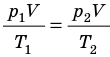
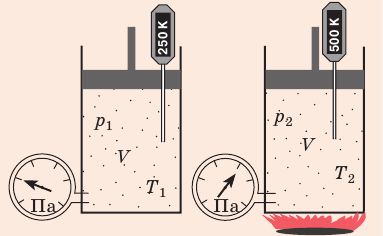
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 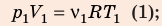
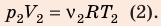

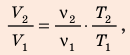
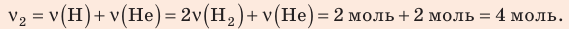
Ответ: примерно в 2,7 раза.
Пример №2
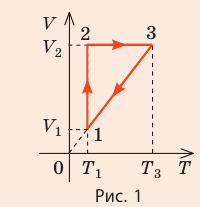
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
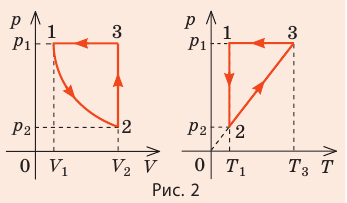
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📺 Видео
Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Уравнение состояния идеального газа. Газовые законыСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение состояния идеального газаСкачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать

ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

Вывод уравнения состояния Клапейрона—МенделееваСкачать

Решение графических задач на тему Газовые законыСкачать

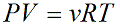
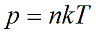
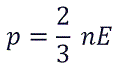
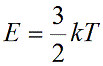
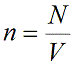
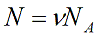
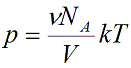
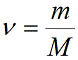
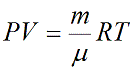


























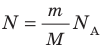
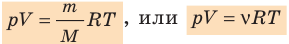
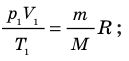
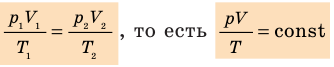
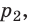
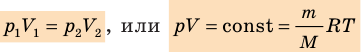

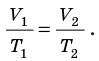
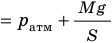
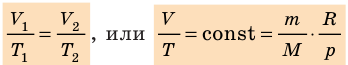
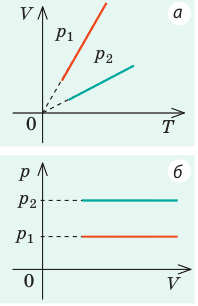

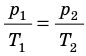
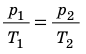
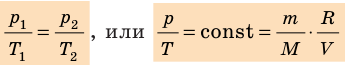

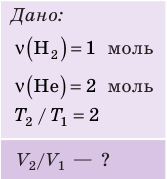
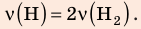

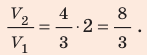
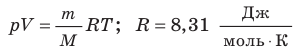 — универсальная газовая постоянная.
— универсальная газовая постоянная.