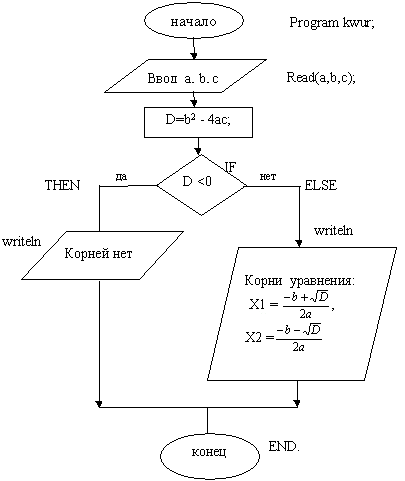
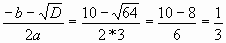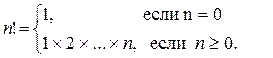Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.
Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами Visual Basic
Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?
Поместим на форму две кнопки: CommandButton1 и CommandButton2.
Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.
Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:
- ввод коэффициентов исходного уравнения a, b, c;
- расчет дискриминанта d=b 2 — 4ac;
- анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
- вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.
Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.
В окне InputBox вводим значение первого коэффициента уравнения a=10.
Ввод первого коэффициента a завершается нажатием кнопки Ok.
Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.
Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.
Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.
Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.
После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.
И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.
Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.
Далее вводим второй коэффициент уравнения b= –8.
Третий коэффициент уравнения c=16 вводим в последнюю очередь.
В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.
Видео:Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать
Составить блок схему алгоритма решения квадратного уравнения
Задача 1. Составить блок-схему и программу, находящие корни квадратного уравнения
ПРОГРАММА на БЕЙСИК
PRINT “Решение квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
d = b * b – 4 * a * c
THEN Х 1=(-b-sqr(d))/(2*a) : Х 2=(-b+sqr(d))/(2*a) : PRINT “Х1=“, Х1, “ Х2=“, Х2
ELSE PRINT “Действительных корней нет “
Запустите программу на выполнение и решите следующие квадратные уравнения:
а) 1125 х 2 – 45 х – 324 = 0
б) 502 х 2 – 38,5 х + 12,125 = 0
в) 16 х 2 – 256 х + 1024 = 0
Задача 2. Составить блок-схему и программу, определяющие количество корней квадратного уравнения
ПРОГРАММА на БЕЙСИК
PRINT “Количество корней квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
d = b * b – 4 * a * c
IF d > 0 THEN PRINT “2 разных корня“ ELSE PRINT “2 одинаковых корня“
ELSE PRINT “Действительных корней нет“
Запустите программу на выполнение и определите количество корней в следующих квадратных уравнениях:
а) 1125 х 2 – 45 х – 324 = 0
б) 502 х 2 – 38,5 х + 12,125 = 0
в) 16 х 2 – 256 х + 1024 = 0
Задача 3*. Составить блок-схему и программу, определяющие имеет ли квадратное уравнение ax 2 + bx + c = 0 хотя бы один корень, больший числа m .
Запустите программу на выполнение и определите имеется ли корень в следующих квадратных уравнениях:
а) 1125 х 2 – 45 х – 324 = 0 при m = 0
б) 502 х 2 – 38,5 х + 12,125 = 0 при m = 15
в) 16 х 2 – 256 х + 1024 = 0 при m = 7
Домашнее задание – Составить блок-схемы и программы для следующих задач:
Задача 1. Определить является ли введенное с клавиатуры число корнем квадратного уравнения ax 2 + bx + c = 0 .
До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование – это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D 0, то два корня)
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D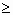
0, то что я получу в случае D=0?
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 – 4ac.
Сравнить его с нулём
D=b 2 -4ac=10 2 -4*3*3=100 – 36 =64
Х1=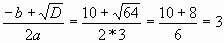
,
X2 = 
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок – схемы применительно к языку программирования.
4. Составление программы по блок – схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Var a,b,c,d,x1,x1: real;
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы – ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
1,5х 2 -0,6х – 4,8 = 0
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File – Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка “3”
2. За проверку работы программы на примерах, представленных учителем оценка “4”
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка “5”
4. Закрыть программу.
Подсказка: Меню File – Exit или ALT+X.
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль – некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет – сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами – Циклическими.
На сегодня наш урок закончен. До свидания.
 |
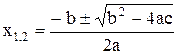Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты a, b, c. Решением в общем случае являются два корня x1 и x2, которые вычисляются по формулам:
Все величины, используемые в этой программе, имеют вещественный тип.
алг корни квадратного уравнения
вещ a, b, c, x1, x2, d
начввод a, b, c
Кон
Слабость такого алгоритма видна «невооруженным глазом». Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам: универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и выходить на конец. Результатом может быть числовой ответ, но может быть и сообщение о том, что при таких данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Это же свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов a, b, c. Вот анализ этой задачи (ограничиваемся только поиском вещественных корней):
если a=0, b=0, c=0, то любое х – решение уравнения;
если a=0, b=0, c¹0, то уравнение решений не имеет;
если a=0, b¹0, то это линейное уравнение, которое имеет одно решение: x=–c/b;
если a¹0 и d=b 2 -4ac³0, то уравнение имеет два вещественных корня (формулы приведены выше);
кв
кв
Кон
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий:
 |
Вначале проверяется «условие» (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется «серия 1» – последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется «серия 2» (отрицательная ветвь). В АЯ условие записывается после служебного слова «если», положительная ветвь – после слова «то», отрицательная – после слова «иначе». Буквы «кв» обозначают конец ветвления.
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «корни квадратного уравнения». В нем для краткости вместо слов «да» и «нет» использованы соответственно «+» и «–».
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала.
Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n – аргумент; i – промежуточная переменная; F – результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n=3.
 |
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.
алгФакториал
целn, i, F
нач ввод n
F:=1; i:=1
пока i£n, повторять
нц F:=F´i
кц
Кон
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда «цикл-пока», или «цикл с предусловием». Общий вид команды «цикл-пока» в блок-схемах и в АЯ следующий:
 |
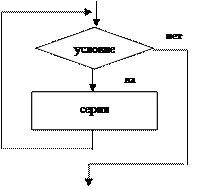Повторяется выполнение серии команд (тела цикла), пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова «нц» и «кц» обозначают соответственно начало цикла и конец цикла.
Цикл с предусловием – это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если a=0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля – еще один признак хорошего качества программы.
 | алгквадратное уравнение вещa, b, c, d, x1, x2 нач повторять ввод a, b, c до a¹0 d:=b 2 –4ac если d³0 тоx1:=(–b+Öd)/(2a) x2:=(–b–Öd)/(2a) вывод x1, x2 иначе вывод “нет вещественных корней” кв кон |
В общем виде структурная команда «цикл с постусловием» или «цикл-до» представляется так:
 |
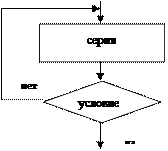Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.
Составим алгоритм решения следующей задачи: даны два натуральных числа M и N. Требуется вычислить их наибольший общий делитель – НОД(M,N).
Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(M N то M:=M–N иначе N:=N–M кв кц кон
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая M=18, N=12. В результате получится НОД=6, что, очевидно, верно.
Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать
Составить алгоритм решения квадратного уравнения ax2 bx c 0 с помощью блок схемы
Copy raw contents
Основные алгоритмические конструкции
Алгоритм применительно к вычислительной машине — точное предписание, т.е. набор операций и правил их чередования, при помощи которого, начиная с некоторых исходных данных, можно решить любую задачу фиксированного типа.
Алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:
Линейный алгоритм — набор команд (указаний), выполняемых последовательно друг за другом.
Основным элементарным действием в линейных алгоритмах является присваивание значения переменной величине. Если значение константы определено видом ее записи, то переменная величина получает конкретное значение только в результате присваивания. Присваивание может осуществляться двумя способами: с помощью команды присваивания и с помощью команды ввода.
Рассмотрим пример. В школьном учебнике математики правила деления обыкновенных дробей описаны так:
- Числитель первой дроби умножить на знаменатель второй дроби.
- Знаменатель первой дроби умножить на числитель второй дроби.
- Записать дробь, числитель которой есть результат выполнения пункта 1, а знаменатель — результат выполнения пункта 2.
В алгебраической форме это выглядит следующим образом:
Построим алгоритм деления дробей для ЭВМ. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, Ь, с, d. Результатом — также целые величины m и n. Блок-схема и текст алгоритма на языке программирования (ЯП) Kotlin приведены ниже.
Формат команды присваивания следующий:
Знак «=» нужно читать как «присвоить».
Команда присваивания обозначает следующие действия, выполняемые компьютером:
- Вычисляется выражение.
- Полученное значение присваивается переменной.
В приведенном выше алгоритме присутствуют две команды присваивания. В блок-схемах команда присваивания записывается в прямоугольнике. Такой блок называется вычислительным блоком.
В описаниях алгоритмов необязательно соблюдать строгие правила в записи выражений. Их можно писать в обычной математической форме. Это еще не язык программирования со строгим синтаксисом.
В приведенном алгоритме присутствуют команды ввода:
В блок-схеме команда ввода записывается в параллелограмме — блоке ввода-вывода. При выполнении данной команды процессор прерывает работу и ожидает действий пользователя. Пользователь должен набрать на устройстве ввода (клавиатуре) значения вводимых переменных и нажать на клавишу ввода Enter. Обычно с помощью команды ввода присваиваются значения исходных данных, а команда присваивания используется для получения промежуточных и конечных величин.
Полученные компьютером результаты решения задачи должны быть сообщены пользователю. Для этих целей предназначена команда вывода:
С помощью этой команды результаты выводятся на экран или на устройство печати на бумагу.
Поскольку присваивание является важнейшей операцией в вычислительных алгоритмах, обсудим ее более подробно.
Рассмотрим последовательное выполнение четырех команд присваивания, в которых участвуют две переменные величины a и b.
В приведенной ниже таблице напротив каждой команды присваивания указываются значения переменных, которые устанавливаются после ее выполнения.
| Команда | a | b |
|---|---|---|
| a=1 | 1 | — |
| b=a*2 | 1 | 2 |
| a=b | 2 | 2 |
| b=a+b | 2 | 4 |
Этот пример иллюстрирует три основных свойства команды присваивания:
- пока переменной не присвоено значение, она остается неопределенной;
- значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующей команды присваивания этой переменной;
- новое значение, присваиваемое переменной, заменяет ее предыдущее значение.
Рассмотрим один очень полезный алгоритм, который приходится часто использовать при программировании. Даны две величины: Х и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было Х=1, Y=2, то после обмена должно стать: Х=2, Y=1.
Хорошей моделью для решения этой задачи является следующая ситуация: имеются два стакана — один с молоком, другой с водой. Требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей: 1) перелить из первого стакана в третий; 2) перелить из второго в первый; 3) перелить из третьего во второй. Цель достигнута!
По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная. Назовем ее Z. Тогда задача обмена решается последовательным выполнением трех команд присваивания:
| Команда | X | Y | Z |
|---|---|---|---|
| ввод X, Y | 1 | 2 | — |
| Z = X | 1 | 2 | 1 |
| X = Y | 2 | 2 | 1 |
| Y = Z | 2 | 1 | 1 |
Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (Х = Y) переменная, стоящая справа (Y), сохраняет свое значение.
Алгоритм для деления дробей имеет линейную структуру. В нем все команды выполняются в строго однозначной последовательности, каждая по одному разу. Линейный алгоритм составляется из команд присваивания, ввода, вывода и обращения к вспомогательным алгоритмам (об этом позже).
При описании алгоритмов в блок-схемах типы, как правило, не указываются (но подразумеваются). В алгоритмах для всех переменных типы указываются явно. В них используются следующие обозначения типов: Int — целый тип, Float — вещественный тип, String — символьный (литерный) тип, Boolean — логический тип. В алгоритме для деления дробей для всех переменных указан тип Int.
Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.
Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторому условию.
Составим алгоритм решения квадратного уравнения: ax 2 +bx+c=0
Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты а, b, с. Решением в общем случае будут два корня х1 и х2, которые вычисляются по формуле:
Слабость такого алгоритма видна невооруженным глазом. Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам, — универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и завершать работу. Результатом может быть число, но может быть и сообщение о том, что при определенных данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Упомянутое свойство называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов а, b, с. Вот анализ рассмотренной выше задачи (ограничиваемся только поиском вещественных корней):
если а = 0, b = 0, с = 0, то любое х — решение уравнения;
если а = 0, b = 0, с О, то уравнение действительных решений не имеет;
если а = 0, b О, то это линейное уравнение, которое имеет одно решение х = -c/b;
если а0 и d=b 2 -4ac >= 0, то уравнение имеет два вещественных корня (формулы приведены выше);
если a0 и d N, то НОД(М, N) = НОД(М-N,N). Другой факт, лежащий в основе алгоритма, тривиален — НОД(М, М) = М. Для «ручного» выполнения этот алгоритм можно описать в форме следующей инструкции:
- Если числа равны, то взять их общее значение в качестве ответа; в противном случае продолжить выполнение алгоритма
- Определить большее из чисел
- Заменить большее число разностью большего и меньшего значений
- Вернуться к выполнению пункта 1
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая М = 18, N = 12. В результате получится НОД = 6, что, очевидно, верно.
Вспомогательные алгоритмы и процедуры
В теории алгоритмов известно понятие вспомогательного алгоритма. Вспомогательным называется алгоритм решения некоторой подзадачи из основной решаемой задачи. В таком случае алгоритм решения исходной задачи называется основным алгоритмом.
В качестве примера рассмотрим следующую задачу: требуется составить алгоритм вычисления степенной функции с целым показателем у = х к , где к — целое число, х0. В алгебре такая функция определена следующим образом:
Для данной задачи в качестве подзадачи можно рассматривать возведение числа в целую положительную степень.
Учитывая, что 1/х -n = (1/х) -n , запишем основной алгоритм решения этой задачи.
Здесь дважды присутствует команда обращения к вспомогательному алгоритму с именем stepen. Это алгоритм возведения вещественного основания в целую положительную степень путем его многократного перемножения. Величины, стоящие в скобках в команде обращения к вспомогательному алгоритму, называются фактическими параметрами.
В котлине вспомогательные алгоритмы оформляются в виде функций. Запишем функцию stepen.
Заголовок вспомогательного алгоритма начинается с ключевого слова fun, после которого следует имя функции, в скобках — список формальных параметров и после скобок тип результата (не обязателен). В списке параметров перечисляются переменные-аргументы с указанием их типов. Здесь x и n — формальные параметры-аргументы. Следовательно, процедура stepen производит вычисления по формуле а к . В основном алгоритме «Степенная функция» обращение к процедуре производится путем указания ее имени с последующим в скобках списком фактических параметров. Между формальными и фактическими параметрами процедуры должны выполняться следующие правила соответствия:
- по количеству (сколько формальных, столько и фактических параметров)
- по последовательности (первому формальному соответствует первый фактический параметр, второму — второй и т.д.)
- по типам (типы соответствующих формальных и фактических параметров должны совпадать)
Фактические параметры-аргументы могут быть выражениями соответствующего типа.
Обращение к процедуре инициирует следующие действия:
- Значения параметров-аргументов присваиваются соответствующим формальным параметрам.
- Выполняется тело процедуры (команды внутри процедуры).
- Значение результата возвращается командой return, и происходит переход к выполнению следующей команды основного алгоритма.
В функции stepen нет команд ввода исходных данных и вывода результатов. Здесь присваивание начальных значений аргументам (x, n) производится через передачу параметров-аргументов. А получение результата происходит командой return. Таким образом, передача значений параметров процедур — это третий способ присваивания (наряду с командой присваивания и командой ввода).
Использование процедур позволяет строить сложные алгоритмы методом последовательной детализации.
Программы для графического отображения алгоритмов
💥 Видео
0.Блок схема. 8 классСкачать
34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать
Решение квадратного уравнения на PythonСкачать
Быстрый способ решения квадратного уравненияСкачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Решение квадратного уравнения ax^2+bx+c=0 с помощью дискриминанта.Скачать
Алгоритм в виде блок схемыСкачать
Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать
Программа, определяющая корни квадратного уравнения. Язык программирования Python.Скачать
Алгоритм решения квадратного уравненияСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать
основы программирования 6 алгоритмы и блок схемыСкачать
Алгоритм решения квадратного уравнения | Алгебра 8 класс #35 | ИнфоурокСкачать
Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Как решать квадратные уравнения без дискриминантаСкачать
