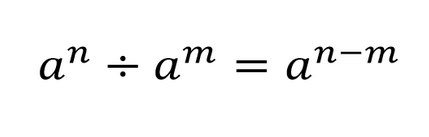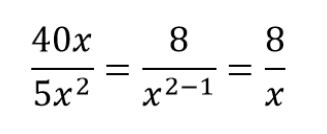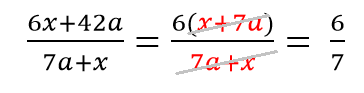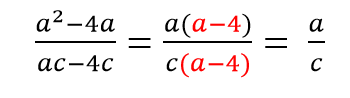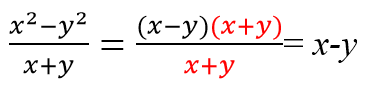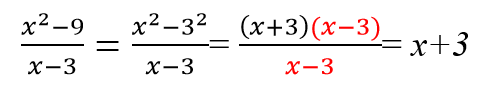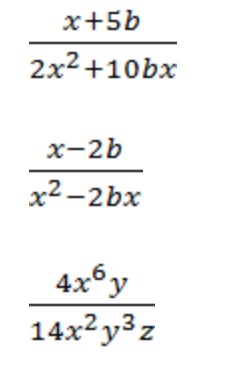О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Определение
- Сокращение алгебраических дробей
- Сокращение алгебраических дробей с многочленами
- Вынесение общего множителя при сокращении дробей
- Сокращение дробей. Формулы сокращенного умножения
- Сокращение алгебраических дробей: правило, примеры.
- Смысл сокращения алгебраической дроби
- Все ли алгебраические дроби подлежат сокращению?
- Правило сокращения алгебраических дробей
- Характерные примеры
- Урок на тему «Разложение квадратного трехчлена на множители. Сокращение дробей» 9 класс
- Выберите документ из архива для просмотра:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📹 Видео
Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Видео:Алгебра 8. Урок 2 - Сокращение дробейСкачать

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
- Определите общий множитель.
- Сократите коэффициенты.
- Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
- Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
- Всегда делим на наименьшее значение в степени
- Вычитаем: 3 — 1
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
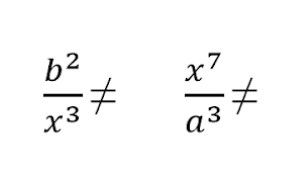 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
- Общий множитель для числителя и знаменателя — 8.
- Х и x 2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
- Общий множитель для числителя и знаменателя — 7.
- b 3 и b делим на b.
- Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Квадратный трехчлен . Сократить дробь.Скачать

Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
- сокращайте многочлен в скобках только с таким же многочленом в скобках;
- сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
| ❌ Так нельзя | ✅ Так можно |
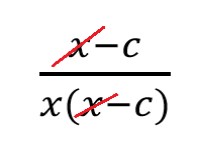 | 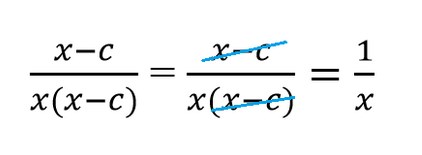 |
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
- Найдите число, на которое делятся числа каждого одночлена.
- Найдите повторяющиеся буквенные множители в каждом одночлене.
- Вынесите найденные буквенные множители за скобку.
- Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
- Выносим общий множитель 6
- Делим 42/6
- Сокращаем получившиеся одинаковые многочлены.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b) 2 = a 2 + 2ab + b 2 |
| Квадрат разности | (a-b) 2 = a 2 — 2ab — b 2 |
| Разность квадратов | a 2 – b 2 = (a – b)(a+b) |
| Куб суммы | (a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 |
| Куб разности | (a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 |
| Сумма кубов | a 3 + b 3 = (a + b)(a 2 — ab+b 2 ) |
| Разность кубов | a 3 — b 3 = (a — b)(a 2 + ab+b 2 ) |
Примеры сокращения дробей с помощью формул сокращенного умножения:
Применяем формулу квадрата разности (a-b) 2 = a 2 — 2ab — b 2 и сокращаем одинаковые многочлены.
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
- Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
- Поделите числитель и знаменатель на общий множитель.
- Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
- Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
- Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
- Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
- Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)
Видео:Преобразование выражений, содержащих кв. корни. Сокращение дробей. Практическая часть. 8 класс.Скачать

Сокращение алгебраических дробей: правило, примеры.
Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.
Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Смысл сокращения алгебраической дроби
В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
Сокращение алгебраической дроби представляет собой аналогичное действие.
Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.
К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х , и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y .
Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Все ли алгебраические дроби подлежат сокращению?
Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 .
С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.
В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 .
В дроби — x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х , или y , или на х · y . И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.
Например, дробь x 3 — 1 x 2 — 1 мы можем сократить на х — 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.
Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Правило сокращения алгебраических дробей
Правило сокращения алгебраических дробей состоит из двух последовательных действий:
- нахождение общих множителей числителя и знаменателя;
- в случае нахождения таковых осуществление непосредственно действия сокращения дроби.
Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.
Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .
Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Характерные примеры
Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:
5 5 = 1 ; — 2 3 — 2 3 = 1 ; x x = 1 ; — 3 , 2 · x 3 — 3 , 2 · x 3 = 1 ; 1 2 · x — x 2 · y 1 2 · x — x 2 · y ;
Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).
К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105
Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105
(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105
По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.
Задана алгебраическая дробь — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необходимо произвести ее сокращение.
Решение
Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:
— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6
Однако, более рациональным способом будет запись решения в виде выражения со степенями:
— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 .
Ответ: — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6
Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).
Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение.
Решение
Возможно сократить дробь таким образом:
2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2
Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК ( 5 , 10 ) = 10 . Тогда получим:
2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .
Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2
Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.
Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Необходимо ее сократить.
Решение
Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:
2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · ( a 2 + 14 · a + 49 ) b 3 · ( a 2 — 49 )
Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:
2 · b 2 · ( a 2 + 14 · a + 49 ) b 3 · ( a 2 — 49 ) = 2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 )
Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · ( a + 7 ) . Произведем сокращение:
2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 ) = 2 · ( a + 7 ) b · ( a — 7 ) = 2 · a + 14 a · b — 7 · b
Краткое решение без пояснений запишем как цепочку равенств:
2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · ( a 2 + 14 a + 49 ) b 3 · ( a 2 — 49 ) = = 2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 ) = 2 · ( a + 7 ) b · ( a — 7 ) = 2 · a + 14 a · b — 7 · b
Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b .
Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.
Дана алгебраическая дробь 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необходимо осуществить ее сокращение, если это возможно.
Решение
На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:
1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2
Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:
x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10
Теперь становится виден общий множитель, осуществляем сокращение:
— 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x
Ответ: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x .
Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Урок на тему «Разложение квадратного трехчлена на множители. Сокращение дробей» 9 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
презентация к уроку.notebook
Выбранный для просмотра документ Чугунова Т. А. — сценарий.doc
Открытый урок для учителей математики Кошкинского района
по алгебре в 9 « В » классе
по теме: « Разложение квадратного трехчлена на множители.
ГБОУ СОШ с. Кошки
Чугуновой Тамары Анатольевны.
Дата проведения 20 октября 2016г.
Тип урока: комбинированный
отработка умения раскладывать квадратный трехчлен на
— формировать умение пользоваться формулами;
— отработать правила сокращения дробей;
— систематизировать знания по теме;
— формировать у учащихся самостоятельность мышления ;
-развивать внимание и логическое мышление;
— прививать интерес к изучению предмета;
— воспитывать уверенность в себе и своих знаниях;
— формировать эстетические навыки при оформлении
записей в тетради;
I . Этап « Организационный » ( слайд 1) (приложение 1)
Учитель: Здравствуйте, ребята! Я рада приветствовать Вас сегодня на нашем уроке. Основная задача урока повторить формулы для решения квадратного уравнения, научиться раскладывать квадратный трехчлен на множители и применять разложение при сокращении дробей, построение графика функции .
Учитель : Математика – это инструмент для решения различных задач. Тому, кто в совершенстве владеет этим инструментом, — под силу справиться с любой проблемой.
II . Этап « Разминка » ( устно )
Для того чтобы нам ничего не упустить давайте повторим все о квадратном
Учитель: 1. Дайте определение квадратного уравнения. (слайд 2)
А в это время один из вас заполнит пропуски у доски.
2. Назовите общий вид квадратного уравнения и его
Занесите коэффициенты квадратного уравнения в таблицу.
3. Какие виды уравнений вы знаете? (слайд 4)
Сгруппируйте уравнения по видам.
4. Как решить полное квадратное уравнение? (слайд 5) (писать )
5. Как вычисляется дискриминант для решения квадратного уравнения?
6. Каким может быть дискриминант? (слайд 6)
Сопоставьте значение дискриминанта и число корней квадратного
7. Запишите формулы вычисления корней квадратного уравнения.(слайд 7)
8. Что называется сокращением дробей ?
9. Что нужно сделать, чтобы сократить дробь ?
( трое работают у доски )
Решить уравнения: 4х 2 – 12х + 9 =0; 5х 2 – 8 х + 4 = 0 ; х 2 + 2 х – 15 = 0
III . Этап « Проверялка »
( самостоятельная работа с комментарием ( слайд 8 )
Решите квадратные уравнения

х 2 + 3 х – 4 = 0 х 2 — 5х – 6 = 0
2х 2 + 4х + 7 = 0 3х 2 + х + 3 = 0
IV . Этап « Вспомнить все »
Учитель: Мы повторили решение квадратных уравнений. Применим полученные знания для разложения квадратного трехчлена на множители с помощью специальной формулы. Если х 1 и х 2 корни квадратного трехчлена ax ² + bx + c , то
ax² + bx + c = a(x – x 1 ) (x – x 2 )
Для того, чтобы разложить квадратный трехчлен на множители, необходимо:
1) найти корни квадратного уравнения;
2) использовать формулу разложения квадратного трехчлена на множители.
Разложение на линейные множители: ( слайд 9 )
Если у квадратного трехчлена ах 2 + bx + c
Нельзя разложить на линейные множители
каждый ученик перед собой имеет таблицу, и во время обсуждения проводит сопоставление
VI . Этап « Научи себя сам »
Учитель: Разложите на линейные множители :
работают у доски два ученика, свое решение проверяют самостоятельно
а) х 2 — 12х+36 = 0 б) 2х 2 — х — 6 = 0
V . Этап « Физкультминутка »
Поднимает руки класс — это « раз »,
Повернулась голова – это « два »,
Руки вниз, вперед смотри – это « три »,
Руки в стороны по шире развернули на « четыре »,
С силой их к плечам прижать – это « пять »,
Всем ребятам надо сесть – это « шесть ».
На конкретном примере вспомним сокращение дробей. Что нужно сделать, чтобы сократить дробь?
Решите № 83 ( а,б) с последующей самопроверкой ( слайд 12 )
Умение сокращать дроби и раскладывать квадратный трехчлен на множители поможем вам при выполнении следующего задания, которое встречается в текстах ОГЭ
Найдите область определения функции и постройте ее график.
У = 
Приравнять трёхчлен к нулю;
Использовать теорему Виета;
Получить выражение сократимое со знаменателем;
Построить график функции;
Выколоть точку на графике
Самостоятельная работа ( слайд 13)
Вариант I Вариант II
1. Разложите на множители квадратный трехчлен :
а) х 2 -2х – 63; а) х 2 + х – 72;
б) 5х 2 -30х + 35; б) 3х 2 — 12х + 3;
в) 17х 2 — 425; в) 12х 2 — 588;
2. Сократите дробь:
у 2 + 5у – 14 а 2 — — 81
5 + 34а – 7а 2 3у – у 2
VIII . Этап « Итоговый »
Учитель: 1. С какой формулой мы сегодня познакомились ?
2. Сформулируйте теорему разложения квадратного трехчлена
3. Каков алгоритм разложения на линейные множители
IX . Этап « Любителям домашнего задания »
П 4, № 87 (а,б) № 84(а,б) №85 (а,б)

Учитель: Ребята, оцените сегодняшний урок.
чувствовал себя комфортно, уроком доволен
Спасибо за урок .
1, Ю. Н. Макарычев, Н. Г. Миндюк, Л.М. Короткова « Дидактические материалы по алгебре 9 класс»
2.М. Б. Миндюк, Н. Г. Миндюк « Разноуровневые дидактические материалы по алгебре 9 класс»
Л. В. Кузнецова, С. Б. Суворова и др. « Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе »
http : // festival @ 1 september.ru
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 952 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 683 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Сократить дробь алгебра 8 классСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 565 448 материалов в базе
Другие материалы
- 25.10.2016
- 635
- 3
- 25.10.2016
- 422
- 0
- 25.10.2016
- 573
- 2
- 25.10.2016
- 297
- 0
- 25.10.2016
- 309
- 0
- 25.10.2016
- 428
- 1
- 25.10.2016
- 359
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 25.10.2016 4459
- RAR 5 мбайт
- 50 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Чугунова Тамара Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 5471
- Всего материалов: 5
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
В России могут объявить Десятилетие науки и технологий
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📹 Видео
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Сокращение дробей. 9 класс.Скачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Преобразование выражений, содержащих квадратные корни, сокращение дробей. Практ. часть. 8 класс.Скачать

Решение биквадратных уравнений. 8 класс.Скачать