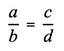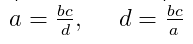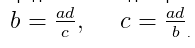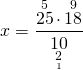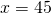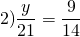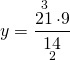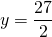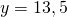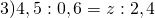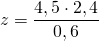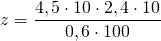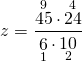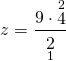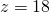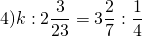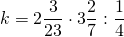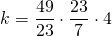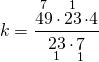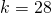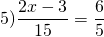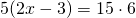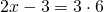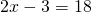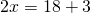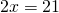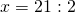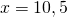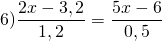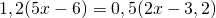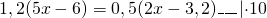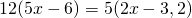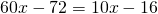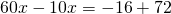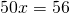Сложные уравнения на пропорции 6 класс (7 видео)

Задачи на пропорции

О чем эта статья:

5 класс, 7 класс, 8 класс

Содержание

Понятие пропорции
Задачи на пропорции с решением и ответами
Составление и решение пропорций в математике
Пропорции — что это в математике
Основное свойство пропорции, правило
Составление и решение пропорций
Примеры уравнений с решением для 6 класса
Решение пропорций
💡 Видео

Видео:Решение уравнений, 6 классСкачать

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Главное свойство пропорции:

Произведение крайних членов равно произведению средних.

где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.

Вывод из главного свойства пропорции:

Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Видео:Пропорция. Основное свойство пропорции. 6 класс.Скачать

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

В этом примере неизвестен крайний член, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

Задание 2. Найти неизвестный член: 1/3 = 5/y

Задача 3. Решить пропорцию: 30/x = 5/8

Задание 4. Решить: 7/5 = y/10

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.

После сокращения отношений получилось: x/y = 2/3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Составим пропорцию: 300/108 = 100/x.

Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

Составим пропорцию: 5/2 = x/450.
Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13

t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

Значит, 30 человек раскрутят канал за 4 дня.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Составление и решение пропорций в математике

Видео:КАК РЕШАТЬ ПРОПОРЦИИ?Скачать

Пропорции — что это в математике

Валя съела 3 яблока из пяти. Какую часть яблок съела Валя?

Вначале узнаем, какую часть яблок составляет 1 яблоко. Всего у Вали было 5 яблок, значит, одно из них — это 1 5 часть всех яблок. Тогда 3 съеденных яблока составляют 3 5 всех яблок.

Тот же ответ получим, если 3 разделим на пять.

Получается, что 3 яблока соотносятся с пятью яблоками как 3 к 5.

Другой вариант записи ответа отмечают в виде десятичной дроби и процентов: 3 5 = 0 , 6 или 60%.

Отношением двух чисел называют частное этих чисел.

Отношение показывает, во сколько раз одно число больше другого. Или какую часть первое число составляет от второго.

Термин «отношение» применяют в случаях, когда нужно выразить одну величину в долях другой. Например, одну площадь в долях другой площади. Это операцию выполняют с помощью деления.

Делимое в выражении отношения называют предыдущим членом. Делитель называют последующим членом.

В задаче 1 предыдущий член — это 3, последующий — 5.

Если есть два равных отношения, то они образуют пропорцию.

Пропорцией называют равенство двух отношений.

Даны два отношения: 3,8:2 и 5,7:3.

Можно ли составить из этих выражений пропорцию?

Найдем значения каждого из отношений:

3 , 8 : 2 = 1 , 9 ; 5 , 7 : 3 = 1 , 9 .

Значения выражений оказались равными, значит, эти отношения равны.

Тогда можно записать равенство: 3,8:2=5,7:3.

Такое равенство называется пропорцией.

Ответ: да, можно составить из этих отношений чисел пропорцию.

С помощью буквенных символов пропорцию можно записать так: a : b = c : d или a b = c d .

Полученное равенство читают: «Отношение a к b равно отношению c к d» или «a относится к b, как c относится к d».

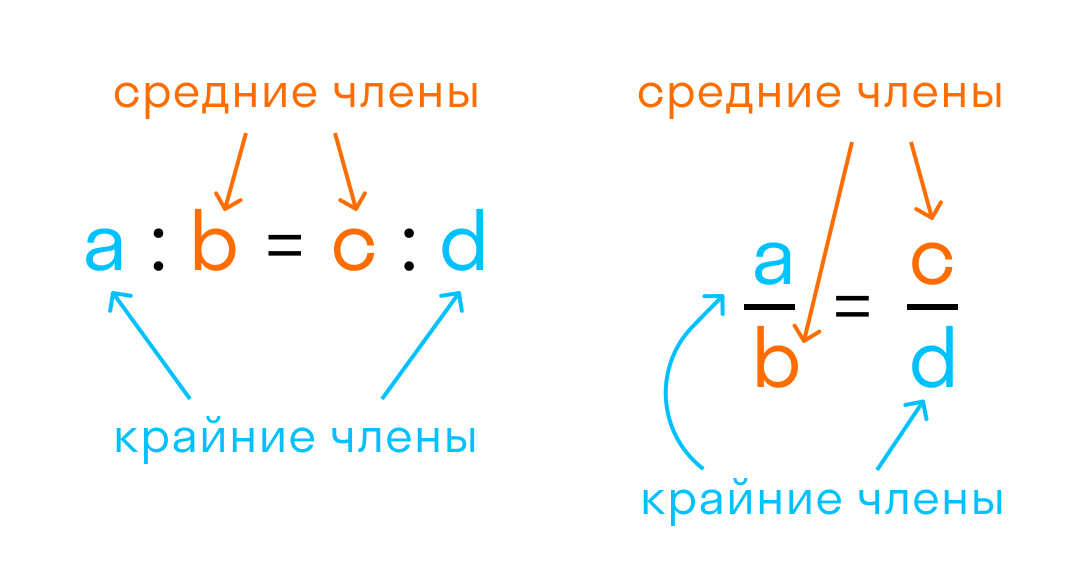
Числа a и d в пропорции называют крайними членами пропорции.

Числа b и c — средними членами пропорции.

Назовите крайние и средние члены пропорции 42:6=49:7.

Крайние члены пропорции — 42 и 7.

Средние члены пропорции — 6 и 49.

Определите средние члены пропорции 25 5 = 35 7 .

Средние члены пропорции — 5 и 35.

Понятие «пропорция» пришло из латинского языка. Слово в переводе означает соразмерность, определенное соотношение частей между собой.

Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 1 часть. 6 класс.Скачать

Основное свойство пропорции, правило

Основное свойство пропорции

В верной пропорции произведение крайних членов равно произведению средних членов:

Определите, верна ли пропорция 6:2=9:3.

В верной пропорции произведение крайних членов равно произведению средних членов.

Произведение крайних членов равно произведению 6 и 3. Получим 6 * 3 = 18 .

Произведение средних членов равно произведению 2 и 9. Получим 2 * 9 = 18 .

Значит, 6:2=9:3. Пропорция верна.

Обратное утверждение тоже верно:

Если произведение средних членов равно произведению крайних членов, то пропорция верна.

Пропорция 60:12=10:2 верна, потому что 60 * 2 = 12 * 10 = 120 .

Если поменять в это пропорции местами средние члены, получим 60:10=12:2. Эта пропорция тоже верна. При перестановке произведение крайних и средних членов не изменилось.

Если в пропорции поменять крайние члены — 2:10=12:60, то произведение тоже не изменится.

Пропорция будет верной, если поменять местами средние члены или крайние члены.

Если какой-то из членов пропорции неизвестен, то его можно найти.

По основному свойству пропорции можно найти ее неизвестный член, если все остальные компоненты известны.

Найдите неизвестный член пропорции: 4,8:b=8:2,5.

Используем основное свойство пропорции: произведение крайних членов = произведению средних членов.

Получим 4 , 8 * 2 , 5 = b * 8 .

b = 4 , 8 * 2 , 5 : 8 ;

Видео:Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

Составление и решение пропорций

Запишите пропорцию: 6 так относится к 18, как 9 относится к 27.

Слово «относится» заменяем на знак деления.

Получаем два отношения: 6:18 и 9:27.

Если эти два отношения равны, то получаем верную пропорцию.

6 : 18 = 9 : 27 ; 1 3 = 1 3 , получили верную пропорцию.

Запишите пропорцию и проверьте ее: отношение 2 к 1 4 равно отношению 3 к 1 15 .

Записываем отношения: 2 1 4 и 3 1 15 .

Составляем пропорцию: 2 1 4 = 3 1 15 .

Проверяем, верна ли пропорция.

Для этого воспользуемся основным свойством пропорции: произведение крайних членов = произведению средних членов.

2 * 1 15 ≠ 1 4 * 3 ; 2 15 ≠ 3 4 . Условие равенства произведений не выполнилось, значит, пропорция не верна.

Определите, верна ли пропорция: 1 , 4 0 , 7 = 3 , 4 1 , 7 .

Чтобы проверить, верна ли пропорция, воспользуемся основным свойством пропорции.

Запишем произведения крайних и средних членов пропорции:

1 , 4 * 1 , 7 = 2 , 38 ; 0 , 7 * 3 , 4 = 2 , 38 .

Значит, произведение крайних членов равно произведению средних членов.

1 , 4 * 1 , 7 = 0 , 7 * 3 , 4 ; 2 , 38 = 2 , 38 .

Вывод: пропорция верна.

Видео:Решение сложных пропорций. Математика 6 класс #пропорция #математика6 #МащенкоНадеждаМихайловнаСкачать

Примеры уравнений с решением для 6 класса

Решите уравнение: 8 , 8 4 2 5 = n 0 , 12 .

Чтобы найти неизвестный член пропорции, используем основное свойство пропорции. Находим произведение крайних и средних членов. Выражаем неизвестный компонент.

8 , 8 4 2 5 = n 0 , 12 ; 8 , 8 * 0 , 12 = 4 2 5 * n . Из равенства выражаем n : n = 8 , 8 * 0 , 12 4 2 5 Представим смешанное число 4 2 5 в виде десятичной дроби. Для этого приведем дробную часть смешанного числа к дроби со знаменателем 10 : домножим числитель и знаменатель 2 . 4 2 5 = 4 2 * 2 н а 5 * 2 = 4 4 10 . Такое смешанное число записываем в виде десятичной дроби, отделяя целую часть запятой: 4 4 10 = 4 , 4 . Тогда n = 8 , 8 * 0 , 12 4 , 4 . Сокращаем получившуюся дробь: 0 , 12 и 4 , 4 делятся на 4 . n = 8 , 8 * 0 , 03 1 , 1 ; 8 , 8 и 1 , 1 делятся на 1 , 1 . n = 8 * 0 , 03 1 ; n = 0 , 24 .

Найдите неизвестный член пропорции: 1 1 2 : 2 1 4 = 6 : m .

Используем основное свойство пропорций. Записываем равенства произведений крайних и средних членов.

1 1 2 * m = 2 1 4 * 6 . И выражаем m : m = 2 1 4 * 6 : 1 1 2 . Переводим смешанные числа в неправильные дроби: m = 2 * 4 + 1 4 * 6 : 1 * 2 + 1 2 ; m = 9 4 * 6 : 3 2 . Натуральное число переводим в обыкновенную дробь со знаменателем 1 и умножаем на первую дробь: m = 9 4 * 6 1 : 3 2 ; m = 9 * 6 4 * 1 : 3 2 . Чтобы разделить обыкновенные дроби, нужно домножить дробь на взаимно обратную данной: m = 9 * 6 4 * 1 * 2 3 ; m = 9 * 6 * 2 4 * 1 * 3 . Сокращаем получившееся выражение. 4 и 2 делятся нацело на 2 . 9 и 3 делятся нацело на 3 . m = 3 * 6 * 1 2 * 1 * 1 . Для чисел 6 и 2 общий делитель 2 : m = 3 * 3 * 1 1 * 1 * 1 ; m = 9 .

Решите уравнение: 0,25:x=3,75:3.

По основному свойству пропорции получим: 0 , 25 * 3 = x * 3 , 75 .

x = 0 , 25 * 3 : 3 , 75 ; x = 0 , 75 : 3 , 75 . Делить на десятичную дробь нельзя. Преобразуем ее в натуральное число.

После запятой в дроби 3 , 75 два знака, значит, нужно домножить ее на единицу с таким оличеством нулей. Это сто.

Но чтобы выражение осталось неизменным, нужно домножить на сто и делимое.

x = 0 , 75 * 100 : 3 , 75 * 100 ; x = 75 : 375 ; x = 0 , 2 .

Найдите неизвестное: k : 3 1 2 = 0 , 4 : 2 4 5

Чтобы найти неизвестный компонент пропорции, нужно воспользоваться основным свойством дроби.

По основному свойству дроби произведение крайних членов равно произведению средних членов.

Получим: k * 2 4 5 = 3 1 2 * 0 , 4 .

Выразим k : k = 3 1 2 * 0 , 4 : 2 4 5 .

Переведем 0,4 в обыкновенную дробь: 0 , 4 = 4 10 . Эта дробь сократима: числитель и знаменатель делятся на 2 нацело: 4 10 = 4 : 2 10 : 2 = 2 5 .

Записываем полученное выражение:

k = 3 1 2 * 2 5 : 2 4 5 .

1 действие — умножение.

Переводим смешанное число в неправильную дробь и умножаем на вторую: числитель на числитель, знаменатель на знаменатель.

3 1 2 * 2 5 = 3 * 2 + 1 2 * 2 5 = 7 2 * 2 5 = 7 * 2 2 * 5 .

Сокращаем дробь: есть одинаковые числа в числителе и знаменателе.

2 действие — деление.

Теперь делим полученное число на 2 4 5 .

Смешанное число переводим в неправильную дробь.

Умножаем 7 5 на взаимно обратную дробь.

7 5 : 2 4 5 = 7 5 : 2 * 5 + 4 5 = 7 5 : 14 5 = 7 5 * 5 14 = 7 * 5 5 * 14 = 7 * 5 5 * 14 = 7 14 = 1 2 = 0 , 5 .

Видео:Метод пропорции ⚖️Скачать

Решение пропорций

Рассмотрим решение пропорций на конкретных примерах.

Решить уравнения с пропорцией:

1) 25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции , произведение крайних членов разделим на известный средний член:

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:

При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.

Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:

В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10: