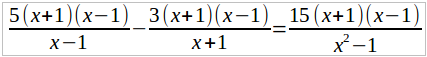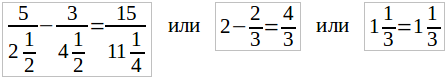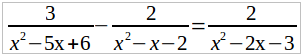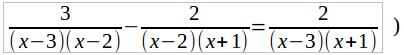Сложное уравнение с ответом 40 (8 видео)

Решение сложных уравнений. 3 класс.

Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.

Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.

Дети уже умеют решать простые уравнения, читай об этом здесь.

А эта статья будет посвящена решению сложных уравнений в 2-3 действия.

Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.

В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.

Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?

Рассмотрим уравнение в 2 действия:

х + 56 = 98 — 2 — оно достаточно легкое.

Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.

х + 56 = 98 — 2

х + 56 = 96 – это простое уравнение. А его решаем очень быстро!

Сейчас мы рассмотрим уравнение:

Такое уравнение можно решить несколькими способами.

У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.

А когда к х + 5 – это число тоже известно.

Закроем его и пусть это будет другое число, например b .

Мы видим, что у нас получилось самое простое уравнение в 1 действие.

2 • b = 30

А чтобы найти а, нам нужно 30 : на 2.

А b не что иное, как х + 5.

х + 5 = 30 : 2

х + 5 = 15

х = 15 – 5

х = 10

Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.

30 – переписываем, а левую часть считаем — будет 30.

30 = 30, значит, уравнение решили правильно.

При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.

Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.

Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.

48 : (16 – а) = 4.

Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.

Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.

16 — а = 48 : 4

16 — а = 12 – это простое уравнение.

а = 16 — 12

а = 4

Проверка: 48 : (16 — 4) = 4

Давайте посмотрим еще одно:

Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.

Проверка: 96 — (16 — 14) = 94

А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.

Рассмотрим уравнение: 36 – (8 • у + 5) = 7

Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.

И вот то, которое вы будете делать третьим, с него и начнем, т.е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.

Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.

По правилам математики в данной записи скобки – не ставим.

8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.

8 • у = 24 – это уравнение простое.

Проверка: 36 — (8 • у + 5) = 7 . Правую часть – 7 — переписываем, а левую считаем.

Итак: 7 = 7. Значит, уравнение решили правильно.

(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8

(36 + d) : 4 = 18 — 8

(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит

36 + d = 40 – уравнение простое и его мы решаем легко!

Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой

Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки. Обязательно напишите в комментариях, какой способ вам более удобен.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 58

Содержание

Математика
Решение задач по математике онлайн
Калькулятор онлайн. Решение показательных уравнений.
Немного теории.
Показательная функция, её свойства и график
Показательные уравнения
🔥 Видео

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

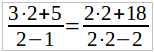
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Видео:Как решить сложные уравненияСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Видео:Проверь мозгСкачать

Немного теории.

Видео:УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, ( a neq 1)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, ( a neq 1), не имеет корней, если ( b leqslant 0), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, ( a neq 1), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2

Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3 х = 7 х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac = 1 ), откуда ( left( frac right) ^x = 1 ), х = 0
Ответ х = 0

Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
( left( frac right) ^ = 1 )
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1