Сколько различных решений имеет уравнение a или b или с 1

Сколько различных решений имеет уравнение

где A, B, C, D – логические переменные?

В ответе не нужно перечислять все различные наборы значений A, B, C, D, при которых выполнено данное равенство. В качестве ответа вам нужно указать количество таких наборов.

Логическое «ИЛИ» истинно , когда истинно хотя бы одно из утверждений.

(D ∧ ¬D)= 0 при любых D.

(A → B)∧ C) = 1 => C = 1; A → B = 1 => ¬ A ∨ B = 1, что дает нам 3 варианта решений при каждом D.

(D ∧ ¬ D)= 0 при любых D, что дает нам два варианта решений (при D = 1, D = 0).

Видео:Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Сколько различных решений имеет уравнение a или b или с 1

РАЗОБРАННЫЕ ПРИМЕРЫ ЗАДАЧ:

Решение. Все “сомножители”2 имеют форму xf=xi+1, они должны быть равны 1. Это значит, что любые два соседних бита должны быть равны. Существует всего две таких цепочки:

Ответ: два решения.

Задача 2. Сколько различных решений имеет система уравнений
(x1 ˅ x2) ˄ ((x1 ˄ x2) → x3) = 1
(x2 ˅ x3) ˄ ((x2 ˄ x3) → x4) = 1
(x3 ˅ x4) ˄ ((x3 ˄ x4) → x5) = 1
(x4 ˅ x5) ˄ ((x4 ˄ x5) → x6) = 1
(x5 ˅ x6) ˄ ((x5 ˄ x6) → x7) = 1
(x6 ˅ x7) ˄ ((x6 ˄ x7) → x8) = 1
(x7 ˅ x8) = 1
где x1,x2,…,x8 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение:
Решим систему с помощью битовых цепочек. Битовая цепочка — это набор единиц и нулей для переменных x1. x8, при которых система будет истинна.

Цепочки строятся по определенным правилам, которые можно вывести из системы. Рассмотрим первое уравнение:

(x1 ˅ x2) ˄ ((x1 ˄ x2) → x3) = 1

Для получения истины выражение (x1 ˅ x2) обязательно должно быть истинно, то есть в уравнении не может быть двух подряд идущих нулей.

Кроме этого, выражение ((x1 ˄ x2) → x3) тоже должно быть истинно. Ложным оно будет в том случае, если x1 и x2 будет равны 1, а x3 — 0. То есть после двух подряд идущих единиц не может быть нуля.

Каждое следующее уравнение связано с предыдущим:

(x1 ˅ x2) ˄ ((x1 ˄ x2) → x3) = 1
(x2 ˅ x3) ˄ ((x2 ˄ x3) → x4) = 1

То есть два правила, которые мы вывели, применяются не только к каждому уравнению, но и ко всей цепочке.

Первая очевидная цепочка для набора иксов — все единицы:

Рассмотрим цепочки, в которых может быть только один нуль. По правилу нуля не может быть после двух единиц:

x1 1 0 1
x2 1 1 0
x3 1 1 1
x4 1 1 1
x5 1 1 1
x6 1 1 1
x7 1 1 1
x8 1 1 1

Рассмотрим цепочки с двумя нулями. По правилу два нуля не могут находиться рядом:

x1 1 0 1 0 1
x2 1 1 0 1 0
x3 1 1 1 0 1
x4 1 1 1 1 0
x5 1 1 1 1 1
x6 1 1 1 1 1
x7 1 1 1 1 1
x8 1 1 1 1 1

Построим оставшиеся цепочки:

x1 1 0 1 0 1 0 1 0 1
x2 1 1 0 1 0 1 0 1 0
x3 1 1 1 0 1 0 1 0 1
x4 1 1 1 1 0 1 0 1 0
x5 1 1 1 1 1 0 1 0 1
x6 1 1 1 1 1 1 0 1 0
x7 1 1 1 1 1 1 1 0 1
x8 1 1 1 1 1 1 1 1 0

Получается, что для данной системы существует 9 различных решений.

Задание: Сколько различных решений имеет система уравнений
((x1 ˄ x2) ˅ (¬x1 ˄ ¬x2)) → ((x3 ˄ x4) ˅ (¬x3 ˄ ¬x4)) = 1
((x3 ˄ x4) ˅ (¬x3 ˄ ¬x4)) → ((x5 ˄ x6) ˅ (¬x5 ˄ ¬x6)) = 1
((x5 ˄ x6) ˅ (¬x5 ˄ ¬x6)) → ((x7 ˄ x8) ˅ (¬x7 ˄ ¬x8)) = 1
((x7 ˄ x8) ˅ (¬x7 ˄ ¬x8)) → ((x9 ˄ x10) ˅ (¬x9 ˄ ¬x10)) = 1
где x1,x2,…,x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Для начала давайте рассмотрим одну из частей нашей системы:

Данное выражение будет истинно, если переменные x1 и x2 будут одновременно равны либо единице, либо нулю, что, фактически, совпадает с таблицей истинности для эквиваленции (тождества). То есть мы его можем записать так:

Упростим так всю нашу систему:
(x1 ≡ x2) → (x3 ≡ x4) = 1
(x3 ≡ x4) → (x5 ≡ x6) = 1
(x5 ≡ x6) → (x7 ≡ x8) = 1
(x7 ≡ x8) → (x9 ≡ x10) = 1

Теперь все стало проще. Обратите внимание, что каждая часть следования вполне самостоятельна, например (x1 ≡ x2) никак не связана переменными с (x3 ≡ x4). То есть мы можем упростить нашу систему еще раз:

A → B = 1
B → C = 1
C → D = 1
D → E = 1

Теперь давайте найдем все возможные комбинации переменных А-Е для этой системы. В импликации (следовании) ложь может быть только в одном случае, если первое выражение истинно, а второе — ложно. То есть при построении цепочек мы должны избежать комбинации 1,0:

A | 1 | 0 | 0 | 0 | 0 | 0
B | 1 | 1 | 0 | 0 | 0 | 0
C | 1 | 1 | 1 | 0 | 0 | 0
D | 1 | 1 | 1 | 1 | 0 | 0
E | 1 | 1 | 1 | 1 | 1 | 0

Переменные A-E в основной системе являются эквиваленцией, то есть на каждую истину или ложь принимают по два различных варианта. То есть для каждого столбца в нашей таблице предусмотрено 25 = 32 варианта.

Например, первый столбец — 1 1 1 1 1, то есть в каждое тождество системы должно давать 1, а это возможно в двух вариантах иксов: 0 ≡ 0 или 1 ≡ 1, то есть на каждую единицу таблицы приходится два варианта. То же самое и с нулями.

Всего в таблице у нас получилось 6 различных цепочек, каждая принимает по 32 варианта, то есть общее количество комбинаций: 6*32=192 комбинации.

Видео:Сколько решений имеет логическое уравнение: (A импликация В) ИЛИ (C импликация D). ЕГЭ(информатика)Скачать

(не A Или B →C) &amp ; (⌐A→⌐C) = 1Сколько решений имеет уравнение?

Информатика | 5 — 9 классы

(не A Или B →C) &amp ; (⌐A→⌐C) = 1

Сколько решений имеет уравнение?

По таблице истинности полуается 4 решения.

Видео:Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать

Упростить выражения : 1?

Упростить выражения : 1.

(A + B)&amp ; (неB + A)&amp ; (неC + B) 3.

(1 + (A + B)) + ((A + C)&amp ; 1) 4.

(A&amp ; B&amp ; неC) + (A&amp ; B&amp ; C) + не(A + B) Повышенный уровень (A + B + C)&amp ; не(A + неB + C).

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Сколько решений имеет уравнение (АВ)↔(АС) = А(А→С), где А, В, С – логические переменные?

Сколько решений имеет уравнение (АВ)↔(АС) = А(А→С), где А, В, С – логические переменные?

Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Найдите значения выражений :1) (1или1)или(1или0)2) ((1или0)или1)или1)3) (0&amp ; 1)&amp ; 14) 1&amp ; (1&amp ; 1)&amp ; 15) ((1или0)&amp ; (1&amp ; 1))&amp ; (0или1)?

Найдите значения выражений :

ЗА ПОДРОБНОЕ РЕШЕНИЕ ДАЮ 25 БАЛЛОВ Используя законы логики упростите выражения : A) (С l ( А &amp ; В) l(не А &amp ; В ) Б) не ((А l В) &amp ; (не С)) B) (А l В &amp ; С ) l ( А lВ &amp ; (не С).

Видео:Урок 27. Логические уравнения. ИКТ 10 класс по ПоляковуСкачать

Помогите решить задачи?

Помогите решить задачи.

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета :

1) Попугай&amp ; (Антилопа | Тапир) 340 Попугай&amp ; Антилопа 220 Попугай&amp ; Тапир 190

Сколько страниц будет найдено по запросу Попугай &amp ; Антилопа &amp ; Тапир

2) Москва&amp ; Лондон 255

Москва&amp ; Париж 222

Москва&amp ; Париж &amp ; Лондон 50

Сколько страниц будет найдено по запросу Москва &amp ; (Париж | Лондон)

3) Пекин&amp ; (Москва | Токио) 338

Пекин&amp ; Москва 204

Пекин&amp ; Токио 184

Сколько страниц будет найдено по запросу Пекин &amp ; Москва &amp ; Токио

4) Лебедь&amp ; (Рак | Щука) 320

Лебедь&amp ; Рак &amp ; Щука 50

5) Пушкин | Лермонтов 5200

Пушкин&amp ; Лермонтов 1200

Сколько страниц будет найдено по запросу Пушкин

6) Фрегат | Эсминец 3400

Фрегат &amp ; Эсминец 900

Сколько страниц будет найдено по запросу Эсминец

7) март &amp ; май 472

май &amp ; апрель 425

май &amp ; (март | апрель) 620

Сколько страниц будет найдено по запросу март &amp ; апрель &amp ; май

8) март &amp ; май &amp ; июнь 150

март &amp ; (май | июнь) 520

Сколько страниц будет найдено по запросу март &amp ; июнь

9) декабрь &amp ; январь &amp ; февраль 113

декабрь &amp ; январь 225

декабрь &amp ; (январь | февраль) 645

Сколько страниц будет найдено по запросу декабрь &amp ; февраль

10) васильки &amp ; ландыши 650

ландыши &amp ; лютики 230

ландыши &amp ; (васильки | лютики) 740

Сколько страниц будет найдено по запросу ландыши &amp ; васильки &amp ; лютики.

Видео:9 класс, 26 урок, Комбинаторные задачиСкачать

Сколько различных решений имеет логическое уравнение?

Сколько различных решений имеет логическое уравнение?

X1 → X2 → X3 → X4 → X5 → X6 = 1.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Найдите значения выражения :1) ((1&amp ; 1)или0)&amp ; (0или1)2) ((0&amp ; 0)или0)&amp ; (1или1)3) (Аили1)или(Вили0)4) ((1&amp ; А)или(В&amp ; 0))или15) 1илиА&amp ; 0?

Найдите значения выражения :

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Сколько различных решений имеет уравнение?

Сколько различных решений имеет уравнение?

Bv! A&amp ; BvA&amp ; B нужно упростить.

Видео:Исследование систем линейных уравнений на совместностьСкачать

Найди значение выражения 1&amp ; 1&amp ; 1&amp ; 1&amp ; 1&amp ; 1?

Найди значение выражения 1&amp ; 1&amp ; 1&amp ; 1&amp ; 1&amp ; 1.

Перед вами страница с вопросом (не A Или B →C) &amp ; (⌐A→⌐C) = 1Сколько решений имеет уравнение?, который относится к категории Информатика. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Учитель информатики

Видео:✓ Сколько же решений? | Опять кто-то неправ #019 | Борис Трушин, Valery Volkov & MindYourDecisionsСкачать

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Видео:Построение таблиц истинностиСкачать

§ 18 Алгебра логики

Информатика. 10 класса. Босова Л.Л. Оглавление

§ 18. Алгебра логики

Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.

Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.

18.1. Логические высказывания и переменные

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно.

Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.

Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?

Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и др.

Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).

Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».

Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем В, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и В». Здесь А, В — логические переменные, «и» — логическая связка.

Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».

Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:

Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

18.2. Логические операции

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Из курса информатики основной школы вам известны логические операции отрицание, конъюнкция и дизъюнкция. Их таблицы истинности представлены ниже.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны, называется конъюнкцией или логическим умножением.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, называется дизъюнкцией или логическим сложением.

Логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному, называется отрицанием или инверсией.

При построении отрицания простого высказывания:

• используется оборот «неверно, что» или к сказуемому добавляется частица «не»;
• в высказывании, содержащем слово «все», это слово заменяется на «некоторые» и наоборот.

Рассмотрим несколько новых логических операций.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией или логическим следованием.

Операция импликации обозначается символом ? и задаётся следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если …, то». Эту связку мы используем тогда, когда хотим показать наличие причинно-следственной связи, иначе говоря, зависимость одного события от другого. Например, пусть некоторый человек сказал: «Если завтра будет хорошая погода, то я пойду гулять». Ясно, что человек окажется лжецом лишь в том случае, если погода действительно будет хорошей, а гулять он не пойдёт. Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.

Результат операции импликации, как и других логических операций, определяется истинностью или ложностью логических переменных, а не наличием причинно-следственных связей между высказываниями. Например, абсурдное с житейской точки зрения высказывание «Если 2 > 3, то существуют ведьмы» является истинным с точки зрения алгебры логики.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.

Строгая дизъюнкция обозначается символом ? и задаётся следующей таблицей истинности:

В русском языке строгой (разделительной) дизъюнкции соответствует связка «либо». В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.

Например, высказывая утверждение «На сегодняшнем матче Петя сидит на трибуне А либо на трибуне Б», мы считаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б, и что сидеть одновременно на двух трибунах Петя не может.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.

В логике эквиваленция обозначается символом и задаётся следующей таблицей истинности:

В разговорной речи для выражения взаимной обусловленности используется связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».

Рассмотрим высказывание «Денис пойдёт в бассейн тогда и только тогда, когда он выучит уроки».

Это высказывание истинно (договорённость соблюдается), если истинны оба элементарных высказывания («Денис пойдёт в бассейн», «Денис выучит уроки»). Высказывание истинно (договорённость не нарушается) и в том случае, если оба элементарных высказывания ложны («Денис не пойдёт в бассейн», «Денис не выучит уроки»). Если же одно из двух высказываний ложно («Денис пойдёт в бассейн, хотя и не выучит уроки», «Денис выучит уроки, но не пойдёт в бассейн»), то договорённость нарушается, и составное высказывание становится ложным.

А сейчас посмотрите внимательно на таблицы истинности строгой дизъюнкции и эквиваленции: если на некотором наборе логических переменных результатом строгой дизъюнкции является истина, то на этом же наборе результатом эквиваленции всегда будет ложь, и наоборот.

Можно сделать выводы:

• операция эквиваленции есть отрицание операции строгой дизъюнкции

• операция строгой дизъюнкции есть отрицание операции эквиваленции

На сегодняшний день в алгебре логики не существует унифицированной символики для обозначения логических операций. В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.

Таблица 4.1

Логические операции и их обозначения

Операция отрицания выполняется над одним операндом. Такие операции называются одноместными или унарными. Все остальные логические операции, представленные в таблице 4.1, выполняются над двумя операндами и называются двуместными или бинарными.

18.3. Логические выражения

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (О, 1), логических переменных, знаков логических операций и скобок.

Для логического выражения справедливо:

1) всякая логическая переменная, а также логические константы (О, 1) есть логическое выражение;
2) если А — логическое выражение, то и 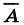— логическое выражение;
3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.

При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.

Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная ? вторая буква согласная) & (последняя буква гласная ? предпоследняя буква гласная):

1) ОЗОН;
2) ИГРА;
3) МАФИЯ;
4) ТРЕНАЖ.

Вычислим значение логического выражения для каждого из данных слов:

Итак, заданному условию удовлетворяют первое и четвёртое слова.

Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.

Пример 2. Решим логическое уравнение

Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:

Таким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0.

Подставим найденные значения переменных в уравнение

Ответ: А = 1, В = 1, С = 0, D = 0.

Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.

Пример 3. Выясним, сколько различных решений имеет логическое уравнение

Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний. Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:

Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.

Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).

Сколько решений имеет исходное уравнение?

Пример 4. Выясним, сколько решений имеет очень простое с виду логическое уравнение х₁ & х₂ ? х₃ & х₄ = 1.

Введём замену переменных. Пусть t₁ = х₁ & х₂, t₂ = х₃ & х₄. Тогда исходное уравнение примет вид: t₁ ? t₂ = 1.

На t₁ никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t₁ и t₂ при которых t₁ ? t₂ = 1.

Получаем для t₁ и t₂ три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х₁ & х₂, вторая — х₃ & х₄. Рассмотрим первый набор: существует три набора х₁ и х₂ таких, что х₁ & х₂ = 0, другими словами, первый 0 мы можем получить тремя способами. Второй О в этом наборе мы также можем получить тремя способами.

Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами.

Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами.

Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (х₃ & х₄ = 1 при х₃ = 1 и х₄ = 1). Следовательно, есть ещё три набора переменных х₁, х₂, х₃, х₄, являющихся решением исходного уравнения.

Самостоятельно доведите решение этой задачи до конца.

18.4. Предикаты и их множества истинности

Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х 2 + у 2 = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x 2 — 3x + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (x 2 — 3x + 2 = 0).

Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката А(х) ? В(х).

Пример 5. Найдём все целые числа 2, превращающие предикат

P(z) = (z > 5) & (z — 2 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката В(z) = (z — 2

Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:

Его мощность |Р| = 11.

Пример 6. Рассмотрим предикат (50 2 ) ? (50 > (х + 1) 2 ), определённый на множестве целых чисел. Найдём множество истинности этого предиката.

Зачастую задания такого рода формулируют несколько иначе.

Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 (х + 1)2)».

Проанализируем отдельно каждый из элементарных предикатов (50 2 ) и (50 > (x + 1) 2 ), решив соответствующие неравенства:

Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):

Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.

САМОЕ ГЛАВНОЕ

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Логические операции имеют следующий приоритет:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.

Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Вопросы и задания

1. Из данных предложений выберите те, которые являются высказываниями. Обоснуйте свой выбор.

1) Как пройти в библиотеку?
2) Коля спросил: «Который час?»
3) Картины Пикассо слишком абстрактны.
4) Компьютеры могут быть построены только на основе двоичной системы счисления.

2. Из каждых трёх выберите два высказывания, являющихся отрицаниями друг друга:

1) «1999 2000», «1999 ? 2000»;
2) «Петя решил все задания контрольной работы», «Петя не решил все задания контрольной работы», «Петя решил не все задания контрольной работы»;
3) «Луна — спутник Земли», «Неверно, что Луна — спутник Земли», «Неверно, что Луна не является спутником Земли »;
4) «Прямая а не параллельна прямой с», «Прямая а перпендикулярна прямой с», «Прямые а и с не пересекаются» (считаем, что прямые а и с лежат в одной плоскости);
5) «Мишень поражена первым выстрелом», «Мишень поражена не первым выстрелом», «Неверно, что мишень поражена не первым выстрелом».

3. Рассмотрите следующие элементарные высказывания: А = «Река Днепр впадает в Чёрное море», В = «45 — простое число», С = «Вена — столица Австрии», D = «0 — натуральное число».

Определите, какие из них истинные, а какие ложные. Составьте сложные высказывания, применяя каждый раз только одну из пяти логических операций

к высказываниям А, В, С и D. Сколько новых высказываний можно получить с помощью отрицания (инверсии)? Конъюнкции? Дизъюнкции? Импликации? Эквиваленции? Сколько всего новых высказываний можно получить? Сколько среди них будет истинных?

4. Представьте каждую пословицу в виде сложного логического высказывания, построенного на основе простых высказываний. Ответ обоснуйте при помощи таблиц истинности.

1) На вкус и цвет товарищей нет.
2) Если долго мучиться, что-нибудь получится.
3) Не зная броду, не суйся в воду.
4) Тяжело в ученье, легко в бою.
5) То не беда, что во ржи лебеда, то беда, что ни ржи, ни лебеды.
6) Где тонко, там и рвётся.
7) Или грудь в крестах, или голова в кустах.
8) За двумя зайцами погонишься — ни одного не поймаешь.
9) И волки сыты, и овцы целы.

5. Подберите вместо А, В, С, D такие высказывания, чтобы полученные сложные высказывания имели смысл:

1) если (А или В и С), то D;
2) если (не А и не В), то (С или D);
3) (А или В) тогда и только тогда, когда (С и не D).

7. Сколько из приведённых чисел Z удовлетворяют логическому условию: ((Z кратно 4) v (Z кратно 5)) ? (Z кратно 6)?
1) 4; 2) 6; 3) 7; 4) 12.

8. Найдите все целые числа Z, для которых истинно высказывание:

9. Какие из высказываний А, В, С должны быть истинны и ка кие ложны, чтобы были ложны следующие высказывания?

10. Даны три числа в различных системах счисления:

Переведите А, В и С в двоичную систему счисления и вы полните поразрядно логические операции (A v В) & С. Отвеп дайте в десятичной системе счисления.

11. Логическое отрицание восьмиразрядного двоичного числа записанное в десятичной системе счисления, равно 217 Определите исходное число в десятичной системе счисления,

12. Определите логическое произведение и логическую сумм> всех двоичных чисел в диапазоне от 16₁₀ до 22₁₀, включая границы. Ответ запишите в восьмеричной системе счисления.

13. Сколько различных решений имеет логическое уравнение?

14. Сколько решений имеет логическое уравнение х₁ & х₂ v х₃ & x₄ = 1?

15. Изобразите в декартовой прямоугольной системе координат множества истинности для следующих предикатов:

16. Предикат ((8x — 6) 65) определён на множестве целых чисел. Найдите его множество истинности. Укажите наибольшее целое число х, при котором предикат превращается в ложное высказывание.

💥 Видео

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

КАК РЕШАТЬ СИСТЕМЫ ЛОГИЧЕСКИХ УРАВНЕНИЙ. ЕГЭ по информатике. Задание 23Скачать

Алфавитный подход к определению количества информацииСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать