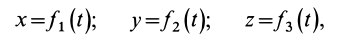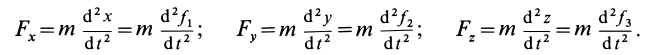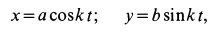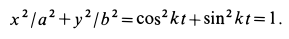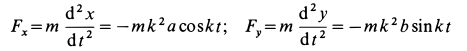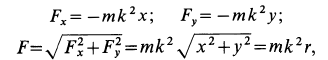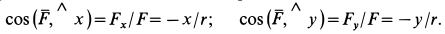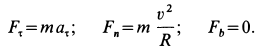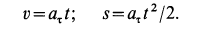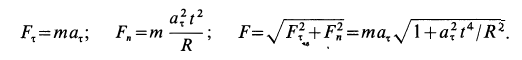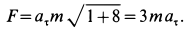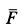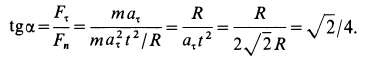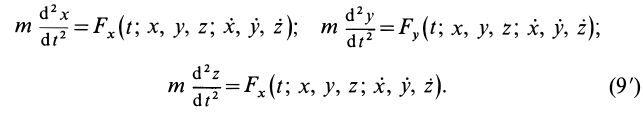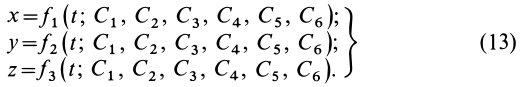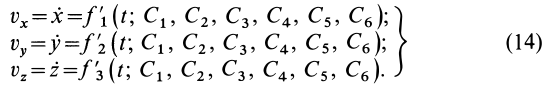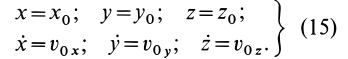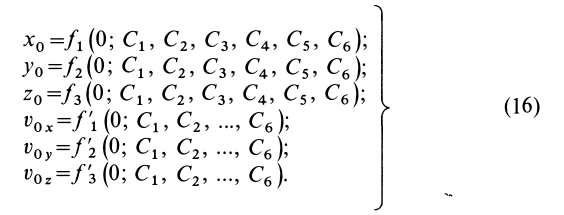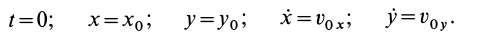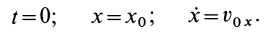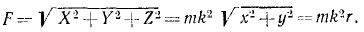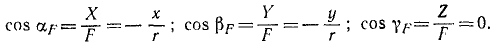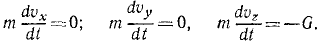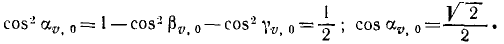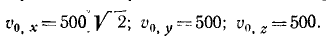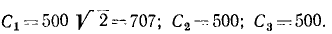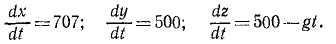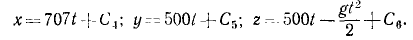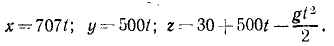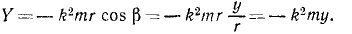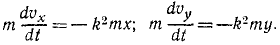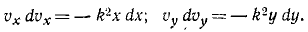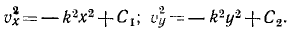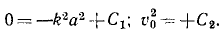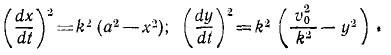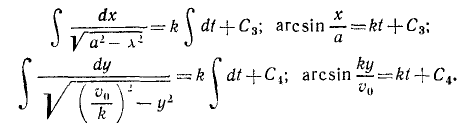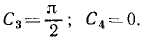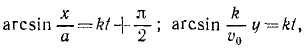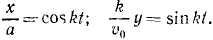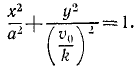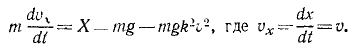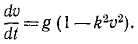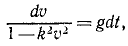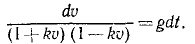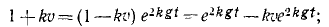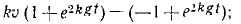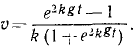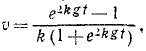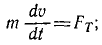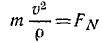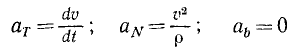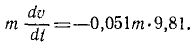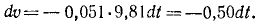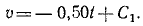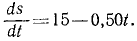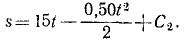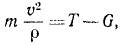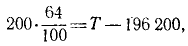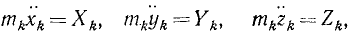Система уравнений движения второго порядка

Содержание:

Две основные задачи динамики точки:

Используя дифференциальные уравнения движения материальной точки в. той или другой системе координат, можно решать две основные задачи динамики точки.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Первая задача

Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, например, заданы уравнения движения точки в декартовой системе координат

то проекции силы на оси координат определяются из дифференциальных уравнений движения точки (9), т. е.

Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.

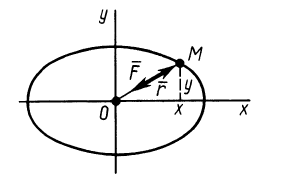
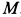
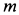
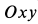
Пример 1. Точка , имеющая массу (рис. 5), движется в плоскости так, что уравнениями ее движения являются

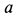
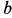
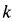
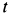
где , , — постоянные положительные величины; — время.

Определить силу, под действием которой точка совершает это движение.

Решение. Найдем уравнение траектории точки в координатной форме, исключая время из уравнений движения:

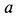
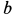
Траекторией точки является эллипс с полуосями и .

Рис. 5

На основании дифференциальных уравнений движения точки (10)

или, если ввести координаты движущейся точки,

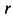
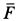
где —радиус-вектор движущейся точки. Косинусы углов силы с осями координат

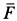
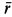
Отсюда можно заключить, что сила имеет направление, противоположное радиусу-вектору . Окончательно

Рис. 6

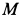
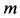
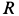
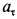
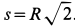
Пример 2. Точка , имеющая массу (рис. 6), движется из состояния покоя по окружности радиусом с постоянным касательным ускорением . Определить действующую на точку силу в момент, соответствующий пройденному точкой по траектории расстоянию .

Решение. Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

Так как движение происходит с постоянным касательным ускорением 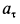без начальной скорости, то

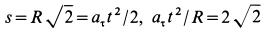
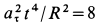
В момент, когда и, следовательно, ,

Тангенс угла 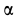между радиусом окружности и силой

Из рассмотрения первой задачи динамики точки видно, что по заданной массе точки и уравнениям ее движения сила полностью определяется как по величине, так и по направлению.

Видео:Решение систем уравнений второго порядка. Практическая часть. 8 класс.Скачать

Вторая задача

По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим решение этой задачи в прямоугольной декартовой системе координат. В общем случае сила 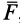, а следовательно, и ее проекции на координатные оси могут зависеть от времени, координат движущейся точки, ее скорости, ускорения и т. д. Для простоты ограничимся случаем зависимости силы и ее проекций на оси координат от времени, координат и скорости. Дифференциальные уравнения движения точки (9) имеют вид

Для нахождения уравнений движения точки в декартовых координатах необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: .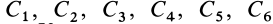

Каждая из координат 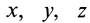движущейся точки после интегрирования системы уравнений (9) зависит от времени t и всех шести произвольных постоянных, т. е.

Если продифференцировать уравнения (13) по времени, то определяются проекции скорости точки на координатные оси:

Таким образом, задание силы не определяет конкретного движения материальной точки, а выделяет целый класс движений, характеризующийся шестью произвольными постоянными. Действующая сила определяет только ускорение движущейся точки, а скорость и положение точки на траектории могут зависеть еще от скорости, которая сообщена точке в начальный момент, и от начального положения точки. Так, например, материальная точка, двигаясь вблизи поверхности Земли под действием силы тяжести, имеет ускорение , если не учитывать сопротивление воздуха. Но точка будет иметь различные скорости и положение в пространстве в один и тот же момент времени и различную форму траектории в зависимости от того, из какой точки пространства началось движение и с какой по величине и направлению начальной скоростью.

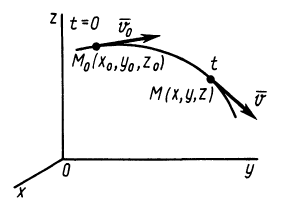
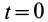
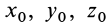
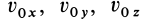
Для выделения конкретного вида движения материальной точки надо дополнительно задать условия, позволяющие определить произвольные постоянные, которых в общем случае будет шесть. В качестве таких условий обычно задают так называемые начальные условия, т.е. в какой-то определенный момент времени, например при (рис. 7), задают координаты движущейся точки и проекции ее скорости :

Рис. 7

Используя эти начальные условия и формулы (13) и (14), получаем шесть следующих уравнений для определения шести произвольных постоянных:

Если система уравнений (16) удовлетворяет условиям разрешимости, то из нее можно определить все шесть произвольных постоянных.

Начальные условия в форме (15) определяют единственное решение системы дифференциальных уравнений (9) при соблюдении соответствующих условий теории дифференциальных уравнений. Условия в других формах, как например, задание двух точек, через которые должна проходить траектория движущейся точки, могут дать или несколько решений, удовлетворяющих этих условиям, или не дать ни одного решения.

При движении точки в плоскости 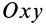имеется два дифференциальных уравнения движения. В решения этих уравнений входят четыре произвольные постоянные. Постоянные определяются из начальных условий

В случае прямолинейного движения точки имеется только одно дифференциальное уравнение и в его решение входят две произвольные постоянные. Для их определения необходимо задать начальные условия:

Задача интегрирования системы дифференциальных уравнений (9′) при заданных начальных условиях в общем случае является довольно трудной. Даже в простейшем случае прямолинейного движения, когда имеется только одно дифференциальное уравнение, его решение удается выразить точно в квадратурах лишь при определенной зависимости силы от времени , координаты и скорости . Поэтому важно определение таких соотношений из системы уравнений (9′), которые являются следствиями этой системы и в которые входят производные от координат точки только первого порядка. Такие соотношения, например, в виде называют первыми интегралами системы дифференциальных уравнений (9′).

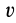
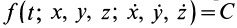
Если из системы (9′) удается найти три независимых первых интеграла, то задача интегрирования упрощается, так как вместо интегрирования системы дифференциальных уравнений второго порядка достаточно проинтегрировать систему трех дифференциальных уравнений первого порядка, которую представляют эти первые интегралы.

В дальнейшем будет рассмотрен способ получения первых интегралов дифференциальных уравнений движения точки из так называемых общих теорем динамики в некоторых частных случаях движения точки.

Для выяснения особенностей решения второй основной задачи динамики, имеющей прикладное значение, рассмотрим ее решение для случая как прямолинейного, так и криволинейного движения материальной точки.

Две основные задачи динамики

Динамика имеет две основные задачи:

1. по заданному движению определить действующие силы
2. по заданным силам определить движение

Прямая и обратная задачи динамики

В динамике изучают механическое движение в связи с силами, приложенными к движущимся объектам. Следовательно, перед динамикой стоят две основные задачи:

1. по движению материального объекта (точки, твердого тела или системы точек) определить силы, производящие, данное движение. Эту задачу называют прямой, или первой основной задачей динамики;
2. вторая задача — обратная по отношению к первой, поэтому ее называют обратной, или второй основной задачей динамики: даны силы, действующие на данный материальный объект; требуется определить движение этого объекта под действием данных сил.

Наиболее просты с механической стороны эти задачи для одной материальной точки, хотя и здесь встречаются большие трудности математического характера.

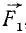
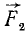
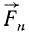
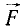
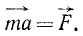
Пусть точка M массы m находится под действием сил, представленных в мгновение t векторами ,, . , или их равнодействующей . Согласно основному закону динамики ускорение, получаемое точкой M от действия сил, направлено по силе и пропорционально ей:

(123)

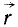
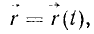
Если решают первую основную задачу динамики точки и движение точки определено в векторной форме, т. е. дан радиус-вектор как некоторая векторная функция времени t:

(54)

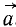
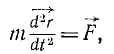
то надо определить по (57) ускорение , выражающееся второй производной от радиуса-вектора точки по времени t, и умножить его на массу т точки. Тогда мы получим следующее выражение основного закона динамики:

(125)

где правая часть даст нам искомую силу.
Если же решают вторую основную задачу динамики точки и задан вектор силы, но требуется определить радиус-вектор как функцию (54) от времени, то для решения задачи нужно интегрировать уравнение (125).

Значительно проще решать такие задачи не в векторной, а в координатной форме.

Все основные теоремы динамики точки могут быть выведены из трех дифференциальных уравнений движения материальной точки в прямоугольных координатах: mx = X; mу = Y; mz =Z

Дифференциальные уравнения движения точки в прямоугольных координатах

Пусть движение точки M задано в прямоугольных координатах кинематическими уравнениями

x = x (t), y = y (t), z = z (t). (58)

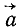
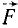
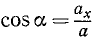
Преобразуем выражение (123) основного закона динамики; для этого определим проекции на оси координат ускорения и силы . Направляющие косинусы (67) ускорения являются вместе с тем и направляющими косинусами силы, так как направление ускорения совпадает с направлением силы. Умножая величины (123) на , получим: ma_x = F cos α.

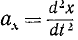
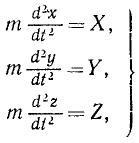
Но согласно (65) . Подставляем это значение и, пользуясь для проекции силы на ось абсцисс (и аналогично для проекций на оси у и z) знакомым нам по статике обозначением, получим

(126)

или, если обозначать вторые производные по времени двумя точками,

mx = X; mу = Y; mz =Z (126 / )

Система трех дифференциальных уравнений (126) второго порядка эквивалентна системе шести дифференциальных уравнений первого порядка:

(127)

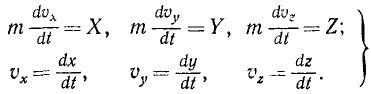
Уравнения (126) или (127) называют дифференциальными уравнениями движения материальной точки в прямоугольных координатах.

Из уравнений движения мы выведем все теоремы динамики. Они дают возможность решить и обе основные задачи динамики точки. В прямой задаче, когда кинематические уравнения движения (58) даны, решение сводится к дифференцированию этих уравнений: умножив на массу вторую производную от координаты но времени, получим проекцию силы. В обратной задаче, когда заданы проекции силы X, Y и Z, а нужно определить координаты точки х, у и z как функции времени (58), решение сводится к интегрированию трех совместных дифференциальных уравнений, где независимым переменным является время.

Три совместных дифференциальных уравнения (126) второго порядка определяют координаты х, у и z в функции времени t. Если движущаяся точка M совершенно свободна, то приложенные к ней силы могут быть функциями ее координат х, у и z, проекций ее скорости х, у и z и времени t:

Проинтегрировать их в общем виде невозможно, но при некоторых видах функции F эти интегралы могут быть получены. В очень многих случаях вычисления возможно проводить на интегрирующих машинах.

При интегрировании дифференциальных уравнений движения материальной точки появляется шесть постоянных интеграции, которые при решении каждой задачи должны быть определены из начальных условий

Постоянные интегрирования

Общие интегралы дифференциальных уравнений движения материальной точки содержат шесть постоянных интеграции: C₁, C₂, C_3, C₄, C₅, C₆. Эти постоянные величины отнюдь не являются произвольными, и в каждой частной задаче, при решении которой приходится интегрировать дифференциальные уравнения движения, постоянные интеграции должны быть определены из начальных условий. Если заданы положение и скорость движущейся точки для какого-либо мгновения t=t₀ (t₀ может быть равным или не равным нулю), то нужно определить постоянные C₁, C₂, C_3, C₄, C₅ и C₆ таким образом, чтобы при t=t₀ координаты х, у и z получили заданные значения х₀, у₀ и z₀ и производные
х, у и z — заданные значения υ_0x, υ_0y, и υ_0z.

Допускают, что данным начальным условиям соответствует только одно движение, конечно, при заданной массе m и силе F. В справедливости этого положения мы -убедимся на всех примерах, которые будем рассматривать, хотя это положение имеет и математическое доказательство. Поэтому, если мы нашли какое-либо движение точки M, удовлетворяющее уравнениям (126) и начальным данным, то, следовательно, мы определили именно то движение, которое искали.

Задача №1

Точка массы т кг движется по винтовой линии согласно кинематическим уравнениям движения: х=r cos kt, у =r sin kt, z=ut, где x, у, z и r выражены в метрах, а t — в секундах; известно, что r, k и и постоянны. Определить величину и направление силы в функции расстояния.

Решение. Задача заключается в определении силы по заданному движению, т. е. является прямой задачей динамики. Условие выражено в физической системе единиц (СИ). При решении будем выражать длину в метрах, мaccy- в килограммах и время — в секундах.

Определим по (126) проекции силы на координатные оси, для чего сначала дважды продифференцируем заданные текущие координаты точек:

х=rk 2 cos kt, у =rk 2 sin kt, z=0

Умножая на т полученные значения проекций ускорения, определим в ньютонах проекции силы:

X= — mk 2 x, Y = — mk 2 y, Z=0

Направляющие косинусы силы найдем по (6):

Ответ. Сила постоянна по величине и перпендикулярна к оси Oz.

Задача №2

Из орудия, стоящего на берегу на высоте 30 ,и над уровнем моря (рис. 160), выпущен снаряд массы m кг со скоростью 1000 м/сек под углом 30° к плоскости горизонта и под углом 60° к линии берега. Пренебрегая сопротивлением воздуха, определить точку, в которой упадет снаряд.

Решение. Единственной силой, действующей па снаряд во время полета, является его вес G = mg. Пo данной силе и по начальным данным (местоположение орудия и начальная скорость снаряда) надо определить движение снаряда и место его падения в морс. Задача относится к обратным задачам динамики. Для ее решения надо составить и проинтегрировать дифференциальные уравнения движения снаряда. Задачу будем решать в единицах СИ. Построим систему координат, взяв за начало точку О, находящуюся под орудием на уровне моря. Ось Ox направим горизонтально, перпендикулярно к берегу в сторону моря, ось Oy— вдоль берега, а ось Oz—вертикально вверх.

Для составления дифференциальных уравнений движения надо знать проекции действующей силы на оси координат. На снаряд после вылета его из орудия действовала только одна сила тяжести G = mg, направленная по вертикали вниз. Проекции действующей силы:

Дифференциальные уравнения движения снаряда напишем в виде (127):

Сокращаем на m, разделяем переменные:

откуда, интегрируя, находим:

Чтобы определить постоянные интеграции, подставим вместо t нуль, а вместо проекций скорости-их начальные значения υ_ox, υ_oy, и υ_oz, соответствующие мгновению t = 0. Получим

Таким образом, три первые постоянные интеграции в нашей задаче равны проекциям начальной скорости снаряда. Чтобы определить числовые значения этих проекций, надо знать направляющие косинусы начальной скорости. Снаряд был выпущен под углом 30° к плоскости горизонта, следовательно, угол ур> 0 начальной скорости с вертикалью равен 60°. Угол β_υ,₀, по условию задачи, тоже равен 60 o , cos _υ,₀ определим из равенства единице Суммы квадратов направляющих косинусов:

Теперь нетрудно определить и проекции начальной скорости:

Мы получили числовые значения постоянных интеграции:

Подставляя эти значения постоянных в уравнения и выражая проекции скоростей по (63), получим три новых дифференциальных уравнения:

Разделив переменные и проинтегрировав, получим

Для определения C₄, C₅ и C₆ подставим и в эти уравнения вместо t его частное значение 0, а вместо х, у и z —их частные значения x₀, у₀ и z₀:

При выбранной нами системе координат имеем x₀ =0; y_{0 =} 0; z₀ = + 30м, следовательно, C₄ = 0; C₅=0; C₆=+30.
Подставляя эти значения в уравнения, полученные после второго интегрирования, найдем кинематические уравнения движения снаряда:

Чтобы определить положение точки, в которой снаряд упадет в море, надо знать продолжительность полета снаряда. Для этого приравняем нулю аппликату z, так как в мгновение, когда снаряд коснется моря, он будет находиться в плоскости хОу. Из уравнения

4,905t 2 — 500t-30 = 0

находим два значения: t=101,6 сек и t=—0,06 сек. Второе значение отбрасываем а первое подставляем в кинематические уравнения движения. Находим ответ.
Ответ. x = 71 831 м — 71,8 км; у = 50 800 м — 50,8 км; z = 0.

Из этого примера видно, что движение точки зависит не только от действующих сил, но и от начальных данных. Если бы начальная скорость или начальные координаты были иными, то и движение снаряда отличалось бы от полученного. Оно по-прежнему было бы равномерным но горизонтали и равнопеременным по вертикали; траекторией снаряда оставалась бы парабола, но она была бы иной и иначе расположенной; иной была бы и точка попадания. Полученные значения постоянных C₁, C₂, . C₆ определены для данной задачи, и при этих значениях постоянных может быть только одно найденное нами решение. Эти постоянные величины вовсе не являются произвольными. Постоянные интеграции, являясь первоначальными значениями переменных, придают решению какой-либо задачи механики всю ту общность, какую она способна иметь.

Вариации постоянных интеграции. Пусть движение какой-либо точки M массы m происходит под действием силы 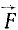. Составив и проинтегрировав дифференциальные уравнения движения точки, определим постоянные интеграции C₁, C₂, . C₆. Тогда, подставляя в полученные уравнения частные значения времени t, мы можем определить положение точки M во всякое данное мгновение. Пусть, например, в мгновение t₁ координаты точки M равны x₁, y₁, z₁. Если мы дадим постоянным интеграции бесконечно малые приращения δC₁, δC₂, . произвольного знака и произвольной величины, называемые вариациями, то положение точки M в то же мгновение t₁, но при измененных постоянных интеграции C₁ + δC₁, C₂ + δC₂, . будет иным. Точка M при неизменившемся времени получит бесконечно малое отклонение, координаты ее получат некоторые бесконечно малые приращения δx₁, δy₁, δz₁, называемые вариациями координат точки, при движении, определяемом величинами C₁, C₂, . постоянных интеграции.

Задача №3

Движение точки весом 2 Г выражается уравнениями x= 3cos2πt см; y=4sinπt см, где t выражено в секундах. Определить проекции силы, действующей на точку, в зависимости от ее координат.

Решение. Задача относится к прямым задачам динамики: по данному движению точки надо определить действующую силу. Для ее решения продифференцируем дважды кинематические уравнения движения точки и, умножив на m найденные х и у, получим X и Y.

Условие дано в технической системе единиц, и в этой задаче примем L в см, F в Г и T сек. Кинематические уравнения движения известны. Дифференцируя дважды, находим

х — 4π 2 3 cos 2πt = — 4π 2 x;
у = —4π 2 sin πt = — π 2 у.

Умножая массу 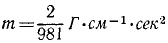на проекции ускорения, найдем проекции силы в граммах. Чтсбы перевести их в ньютоны, надо умножить число граммов на 0,00981.

Решим теперь эту же задачу в физической системе единиц. Принимать за основные единицы метр, килограмм и секунду в этой задаче нецелесообразно. Выразим L в см, M в г и T в сек.

В условии задачи дан вес точки G = 2 Г. Следовательно, ее масса m = 2 г. Умножая проекции ускорения на массу, выраженную в граммах, получим проекции силы в динах:

X = — 8π 2 x = — 78,88x [дин];
Y = — 2π 2 y = — 19,72y [дин].

Чтобы выразить их в ньютонах, надо число дин поделить на 100000.

Ответ. X =— 0,08χ Г = —78,88x дин = —0.0007888x н;
Y = —0,02x Г =— 19,72y дин = —0,0001972y н.

Обратим внимание на одно обстоятельство, которое легко усмотреть в только что решенной задаче. Определяя силу по заданному движению материальной точки, мы нашли, что движение произведено силой, являющейся функцией координат точки. Но мы могли бы выразить силу и как функцию времени. В самом деле, продифференцировав дважды кинематические уравнения движения и умножив вторые производные на m, найдем

X = — 12rnπ 2 cos 2πt; Y = —4rnπ 2 sin πt.

Так одно и то же движение может совершаться под действием различно выраженной силы.

Из этого же примера видно, что если точка движется в одной плоскости, то, приняв эту плоскость за плоскость хОу, можно описать движение точки системой первых двух дифференциальных уравнений движения (126′); третье же дифференциальное уравнение становится лишним.

Задача №4

Найти плоскую траекторию точки M массы m, притягиваемой к неподвижному центру О с силой, пропорциональной расстоянию r и равной k 2 mr, при следующих начальных данных:

Решение. Задача относится к обратным задачам динамики: по заданной силе определить движение. Точка M описывает плоскую траекторию, и нам понадобятся только два уравнения движения.

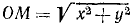
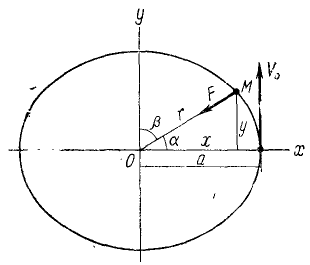
Если в какое-либо мгновение t точка M имела координаты х и у и находилась от центра на расстоянии (рис. 161), то проекции силы на оси координат:

Рис. 161

Дифференциальными уравнениями движения точки являются:

Сократим на т и умножим первое из уравнений на υ_xdt=dx, а второе—на υ_ydt = dy:

Интегрируем и умножаем на 2:

Для определения постоянных интеграции C₁ и C₂ подставляем в эти уравнения вместо переменных величин их начальные значения:

Значения постоянных вносим в уравнения, одновременно выражая υx и υy по (63):

Извлекаем квадратные корни, разделяем переменные н интегрируем:

Для определения постоянных интеграции C₃ и C₄ подставляем в эти уравнения вместо переменных величин t, х и у их начальные значения:

Эти значения постоянных интеграции вносим в уравнения:

Мы получили кинематические уравнения движения (58) точки в декартовых координатах. Чтобы определить траекторию, надо из них исключить время. Возводя в квадрат и складывая, получаем уравнение траектории

Ответ. Эллипс с полуосями a и .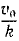

В еще более частном случае, когда сила имеет постоянное направление, а начальная скорость направлена по силе или равна нулю, движение точки прямолинейно. Направив ось Ox по этой траектории, мы обойдемся первым из уравнений (126), которое и нужно интегрировать, чтобы получить закон (58 , ) искомого движения точки. При этом нельзя забывать, что под X мы понимаем не силу, а ее проекцию F cos a, которая в данном случае по величине равна модулю силы. Если α = 0, то сила направлена в сторону положительной оси Ох, и тогда Х>0. Если же α = π, то сила направлена в сторону отрицательного направления оси Ох, тогда X 2 υ 2 .

Решение. Предположим, что тело начинает падать из начального положения О, и направим вниз из точки О ось Ох. Так как движение прямолинейное, то для его определения достаточно первого уравнения (126). На падающее тело действуют две силы: 1) постоянная сила G = mg, направленная в положительную сторону оси Ох, и 2) переменная сила R = mgk 2 υ 2 , являющаяся функцией скорости; она возрастает пропорционально квадрату скорости и направлена против скорости, а следовательно, против положительного направления оси Ох. Имеем

Перепишем это уравнение, сократив его на m:

Из этого уравнения видно, что падение не может быть равноускоренным, что по мере возрастания скорости сила сопротивления увеличивается, правая часть уравнения уменьшается и ускорение стремится к нулю.

Чтобы взять интеграл, перемножим соответственно левые и правые части этого уравнения и следующего выражения:

Это уравнение позволяет определить скорость падающего тела во всякое данное мгновение t. Оно уточняет известную формулу υ=gt, так как здесь учтено и сопротивление воздуха.

Ответ.

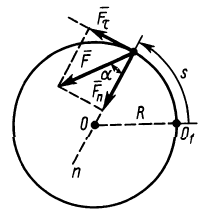
Движение точки можно описать в проекциях на оси естественного трехгранника двумя уравнениями:

Дифференциальные уравнения движения материальной точки в форме Эйлера. В кинематике мы изучали три способа определения движения точки: 1) векторный, 2) в прямоугольных координатах, 3) естественный. Соответственно и в динамике мы можем определить движение точки по заданным силам (или силы по заданному движению) векторным уравнением (125), в проекциях на прямоугольные оси — уравнениями (126), а также естественными уравнениями движения. Из многих форм уравнений движения эти три применяют наиболее часто.

Проецируя ускорение на оси естественного трехгранника, мы нашли (см. § 23), что проекции ускорения на касательную а_N, на главную нормаль αv и на бинормаль a_b выражаются следующими формулами:

и вместо трех составляющих полное ускорение имеет только две. Но сила всегда направлена по ускорению точки, а следовательно, проецируя силу на оси естественного трехгранника, мы и здесь получим только две составляющие (F_T — на касательную и F_N— на главную нормаль) и определим движение точки только двумя уравнениями:
(128)

Задача №6

Горнолыжник в конце склона развил скорость 54 км/ч, после чего свободно скользил по горизонтальному прямолинейному участку пути. Определить длину и время свободного скольжения, если коэффициент трения лыж по снегу f’ = 0,051.

Решение. В задаче примем единицы СИ; тогда вес лыжника, выраженный в ньютонах, G = 9,81 ∙m, где m — его .масса в кг. Задача является обратной задачей динамики, так как требуется определить движение по заданной силе F_гp— f’G. Достаточно одного первого из уравнений (128), потому что движение прямолинейное. Проекция силы имеет отрицательный знак, так как сила трения направлена против скорости, а скорость направлена в положительном направлении (в сторону возрастания расстояния): .

Сокращаем на m и разделяем переменные:

Чтобы определить постоянную C₁, подставим вместо t нуль, а вместо υ—начальное значение скорости —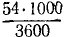= 15 м/сек:

Подставляя это значение C₁ в уравнение, полученное после интегрирования, и заменяя υ по (53), получим новое дифференциальное уравнение:

Разделим переменные и проинтегрируем:

В начальное мгновение лыжник не прошел еще никакого расстояния по горизонтальному участку, а потому C₂ = 0. Время скольжения до остановки определим, положив в уравнении, полученном для скорости,

15 — 0,50t=0, откуда t = 30.

Подставляя это значение t в последнее уравнение, найдем длину свободного скольжения.

Ответ. Время скольжения 30 сек, длина 225 м.

Задача №7

Маятник Борда для определения ускорения свободно падающих тел представляет собой латунный шарик массой 200 г, подвешенный на очень тонкой проволоке длиной 100 см. При качании шарик в наинизшем положении имеет скорость 8 см/сек. Определить натяжение проволоки в ее нижнем конце при наинизшем положении маятника.

Решение. В задаче применена физическая система единиц. Примем L в см, M в г, T в сек.

Задача относится к прямым задачам динамики. Чтобы по данному движению латунного шарика, принимаемого за материальную точку, определить действующую силу, напишем второе из естественных уравнений движения материальной точки (128). В наинизшем положении на шарик действует сила натяжения проволоки, проекцию которой T будем считать положительной, так как она направлена внутрь траектории, и сила тяжести G = 200 . 981 дин, проекцию которой будем считать отрицательной:

или, подставляя числовые значения,

откуда получаем ответ.
Ответ. T = 196 328 дин = 1,96328 н.

Движение точки в плоскости можно описать двумя уравнениями в полярных координатах.

Уравнения движения точки в полярных координатах

В ряде задач бывает удобно исследовать движение точки в полярных координатах. Примем без доказательства, что проекция ускорения точки на полярный радиус-вектор равна (r — rφ 2 ), а на перпендикулярное направление равна (rφ + 2rφ). Помножив на массу эти проекции ускорения точки и приравняв проекциям силы, напишем дифференциальные уравнения движения точки в полярных координатах:

(129)

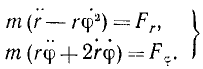
где m_k—масса k-й точки, x_k, y_k и z_k-проекции ее ускорения, a X_k, Y_k и Z_k—проекции равнодействующей всех сил, приложенных к этой точке (k = 1, 2, 3, . n).

Далеко не всегда действующие силы бывают известны. Обычно остаются неизвестными внутренние силы. Для вывода некоторых общих теорем динамики и при решении некоторых частных задач бывает удобным выделить внутренние силы уже при написании дифференциальных уравнений движения.

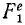
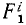
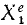
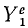
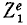
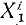
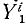
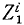
Рассмотрим сначала одну из материальных точек системы, например точку с индексом 1 <k= 1), и распределим все силы, приложенные к этой точке, на две группы: внешние и внутренние. Сложив все внешние силы, действующие на эту точку, получим их равнодействующую , а сложив все внутренние, получим равнодействующую внутренних сил . Проекции этих сил обозначим ,, и ,, .

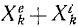
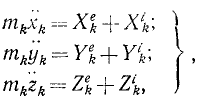
Аналогично поступим с силами, приложенными к остальным точкам, и заменим в написанных выше уравнениях проекции равнодействующей X_k суммой , то же сделаем по двум другим осям. Тогда дифференциальные уравнения примут вид:

(130)

Следовательно, движение свободной механической системы, состоящей из n материальных точек, определяется системой 3n дифференциальных уравнений второго порядка.

Если система не свободна, а на нее наложены связи, выражающие некоторую зависимость между координатами точек механической системы, то бывает возможным сократить число дифференциальных уравнений движения, о чем будет подробнее сказано в § 52 и § 53.

В ряде случаев оказывается целесообразным разделить все силы, действующие на материальные точки механической системы на две категории по иному признаку, а именно на активные силы и реакции связей. Как уже было сказано, реакции связей часто зависят от движения системы и не могут быть найдены, пока не определено движение системы. 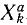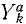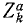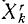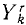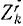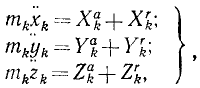Обозначая проекции равнодействующей всех активных сил, действующих на k-ю точку, , и , а проекции равнодействующей всех реакций связей, приложенных к k-й точке, , и , получим:

(130′)

Во всем вашем курсе (если это специально не оговорено) рассмотрены только свободные механические системы и механические системы с идеальными связями. Понятие идеальных связей нам уже встречалось в статике (см. § 4) и будет уточнено в динамике (см. § 51).

В дальнейшем из дифференциальных уравнений (130) и (130′) мы выведем общие теоремы динамики таких материальных систем.

Решение многих проблем по динамике механических систем сопряжено с большими трудностями математического характера. Интегрирующие машины в очень многих случаях дают возможность преодолеть эти трудности.

• Прямолинейное движение точки
• Криволинейное движение материальной точки
• Движение несвободной материальной точки
• Относительное движение материальной точки
• Сложение движение твердого тела
• Кинематика сплошной среды
• Аксиомы классической механики
• Дифференциальные уравнения движения материальной точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Система уравнений движения второго порядка

Системой дифференциальных уравнений называется система вида

где x — независимый аргумент,

y_i — зависимая функция, ,

Функции y_i(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.

Численные методы решения систем дифференциальных уравнений.

Модифицированный метод Эйлера.

Метод Рунге-Кутта четвертого порядка.

Дифференциальным уравнением второго порядка называется уравнение вида

Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Численно ищется частное решение уравнения (2), которое удовлетворяет заданным начальным условиям, то есть решается задача Коши.

Для численного решения дифференциальное уравнение второго порядка преобразуется в систему двух дифференциальных уравнений первого порядка и приводится к машинному виду (3). Для этого вводится новая неизвестная функция , слева в каждом уравнении системы оставляют только первые производные неизвестных функций, а в правых частях производных быть не должно

.

(3)

Функция f₂(x, y₁, y) в систему (3) введена формально для того, чтобы методы, которые будут показаны ниже, могли быть использованы для решения произвольной системы дифференциальных уравнений первого порядка. Рассмотрим несколько численных методов решения системы (3). Расчетные зависимости для i+1 шага интегрирования имеют следующий вид. Для решения системы из n уравнений расчетные формулы приведены выше. Для решения системы из двух уравнений расчетные формулы удобно записать без двойных индексов в следующем виде:

Метод Рунге-Кутта четвертого порядка.

где h — шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: i=0, x=x₀, y₁=y₁₀, y=y₀.

Контрольное задание по зачетной работе.

Колебания с одной степенью свободы

Цель. Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.

Задание. Численно и аналитически найти:

1. закон движения материальной точки на пружинке х(t),
2. закон изменения силы тока I(t) в колебательном контуре (RLC — цепи) для заданных в табл.1,2 режимов. Построить графики искомых функций.

Свободные незатухающие колебания

Затухающее колебательное движение

Предельное апериодическое движение

Вынужденное колебание без сопротивления

Вынужденное колебание без сопротивления, явление резонанса

Вынужденное колебание с линейным сопротивлением

Вынужденное колебание с линейным сопротивлением, явление резонанса

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Системы дифференциальных уравнений

Этот раздел мы решили посвятить решению систем дифференциальных уравнений простейшего вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2 , в которых a 1 , b 1 , c 1 , a 2 , b 2 , c 2 — некоторые действительные числа. Наиболее эффективным для решения таких систем уравнений является метод интегрирования. Также рассмотрим решение примера по теме.

Решением системы дифференциальных уравнений будет являться пара функций x ( t ) и y ( t ) , которая способна обратить в тождество оба уравнения системы.

Рассмотрим метод интегрирования системы ДУ d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2 . Выразим х из 2 -го уравнения системы для того, чтобы исключить неизвестную функцию x ( t ) из 1 -го уравнения:

d y d t = a 2 x + b 2 y + c 2 ⇒ x = 1 a 2 d y d t — b 2 y — c 2

Выполним дифференцирование 2 -го уравнения по t и разрешим его уравнение относительно d x d t :

d 2 y d t 2 = a 2 d x d t + b 2 d y d t ⇒ d x d t = 1 a 2 d 2 y d t 2 — b 2 d y d t

Теперь подставим результат предыдущих вычислений в 1 -е уравнение системы:

d x d t = a 1 x + b 1 y + c 1 ⇒ 1 a 2 d 2 y d t 2 — b 2 d y d t = a 1 a 2 d y d t — b 2 y — c 2 + b 1 y + c 1 ⇔ d 2 y d t 2 — ( a 1 + b 2 ) · d y d t + ( a 1 · b 2 — a 2 · b 1 ) · y = a 2 · c 1 — a 1 · c 2

Так мы исключили неизвестную функцию x ( t ) и получили линейное неоднородное ДУ 2 -го порядка с постоянными коэффициентами. Найдем решение этого уравнения y ( t ) и подставим его во 2 -е уравнение системы. Найдем x ( t ) . Будем считать, что на этом решение системы уравнений будет закончено.

Найдите решение системы дифференциальных уравнений d x d t = x — 1 d y d t = x + 2 y — 3

Начнем с первого уравнения системы. Разрешим его относительно x :

x = d y d t — 2 y + 3

Теперь выполним дифференцирование 2 -го уравнения системы, после чего разрешим его относительно d x d t : d 2 y d t 2 = d x d t + 2 d y d t ⇒ d x d t = d 2 y d t 2 — 2 d y d t

Полученный в ходе вычислений результат мы можем подставить в 1 -е уравнение системы ДУ:

d x d t = x — 1 d 2 y d t 2 — 2 d y d t = d y d t — 2 y + 3 — 1 d 2 y d t 2 — 3 d y d t + 2 y = 2

В результате преобразований мы получили линейное неоднородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами d 2 y d t 2 — 3 d y d t + 2 y = 2 . Если мы найдем его общее решение, то получим функцию y ( t ) .

Общее решение соответствующего ЛОДУ y 0 мы можем найти путем вычислений корней характеристического уравнения k 2 — 3 k + 2 = 0 :

D = 3 2 — 4 · 2 = 1 k 1 = 3 — 1 2 = 1 k 2 = 3 + 1 2 = 2

Корни, которые мы получили, являются действительными и различными. В связи с этим общее решение ЛОДУ будет иметь вид y 0 = C 1 · e t + C 2 · e 2 t .

Теперь найдем частное решение линейного неоднородного ДУ y

d 2 y d t 2 — 3 d y d t + 2 y = 2

Правая часть записи уравнения представляет собой многочлен нулевой степени. Это значит, что частное решение будем искать в виде y

= A , где А – это неопределенный коэффициент.

Определить неопределенный коэффициент мы можем из равенства d 2 y

= 2 :
d 2 ( A ) d t 2 — 3 d ( A ) d t + 2 A = 2 ⇒ 2 A = 2 ⇒ A = 1

Таким образом, y

= 1 и y ( t ) = y 0 + y

= C 1 · e t + C 2 · e 2 t + 1 . Одну неизвестную функцию мы нашли.

Теперь подставим найденную функцию во 2 -е уравнение системы ДУ и разрешим новое уравнение относительно x ( t ) :
d ( C 1 · e t + C 2 · e 2 t + 1 ) d t = x + 2 · ( C 1 · e t + C 2 · e 2 t + 1 ) — 3 C 1 · e t + 2 C 2 · e 2 t = x + 2 C 1 · e t + 2 C 2 · e 2 t — 1 x = — C 1 · e t + 1

Так мы вычислили вторую неизвестную функцию x ( t ) = — C 1 · e t + 1 .

Ответ: x ( t ) = — C 1 · e t + 1 y ( t ) = C 1 · e t + C 2 · e 2 t + 1

🌟 Видео

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение систем уравнений методом подстановкиСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Как решают уравнения в России и СШАСкачать