Выше (6.5, случай 6) было установлено, что
| Геометрической формой условия равновесия произвольной пространственной системы сил является равенство нулю ее главного вектора и главного момента |
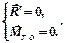
Учитывая, что 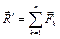



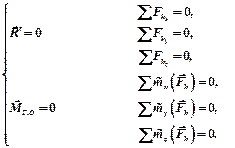
Последние три уравнения имеют место из-за того, что проекция момента силы относительно точки на ось, которая проходит через эту точку, равна моменту силы относительно оси (формула (6.9)).
| Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на три координатные оси и суммы моментов всех сил системы относительно этих координатных осей равнялись нулю. |
Вывод. При решении задач на равновесие произвольной пространственной системы сил, которая приложена к твердому телу, мы должны составить шесть уравнений равновесия (6.19), потому имеем возможность с помощью этих уравнений определить шесть неизвестных величин.
Рассмотрим случай пространственной системы параллельных сил. Систему координат выберем так, чтобы ось Оz была параллельна линиям действия сил (рис. 6.11).
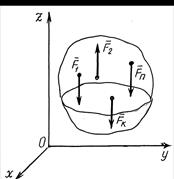 Рисунок 6.11 Рисунок 6.11 | Если система сил находится в равновесии, то имеют место уравнения (6.19). Система сил, показана на рис. 6.11, является упрощенным вариантом произвольной пространственной системы сил, потому и уравнения (6.19) должны упроститься. Выясним, какие из уравнений (6.19) в данном случае выполняются тождественно, то есть является лишними. Такими является: – суммы проекций сил на оси Оx и Оy, потому что силы 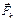 им перпендикулярны; – сумма моментов сил относительно оси Оz, потому что силы им перпендикулярны; – сумма моментов сил относительно оси Оz, потому что силы 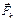 параллельны ей (п. 6.3. Рекомендации для практического занятия). параллельны ей (п. 6.3. Рекомендации для практического занятия). |
Таким образом, остались три уравнения:
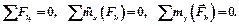
| Для равновесия параллельной пространственной системы сил необходимо и достаточно, чтобы: – сумма проекций сил системы на ось параллельную силам равнялась нулю; – суммы моментов сил системы относительно двух других осей равнялись нулю. |
Вывод. При решении задач на равновесие параллельной пространственной системы сил, которая приложена к твердому телу, мы должны составить три уравнения равновесия и имеем возможность с помощью этих уравнений определить три неизвестных величины.
На первой лекции по разделу «Статика» мы выяснили, что имеют место шесть разновидностей систем сил, которые могут встретиться в Вашей практике инженерных расчетов. Кроме того есть две возможности расположения пар сил : в пространстве и в плоскости. Сведем все уравнения равновесия для сил и для пар сил в одну таблицу (табл. 6.2), в которой в последней колонке отметим количество неизвестных величин, которые позволит определить система уравнений равновесия.
Таблица 6.2 – Уравнения равновесия разных систем сил
| Вид системы сил | Уравнения равновесия | Количество определяемых неизвестных |
Сходящаяся плоская 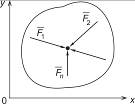 |  | |
Параллельная плоская (  оси 0у) оси 0у)  | 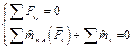 т. А – произвольная, принадлежащая плоскости 0ху т. А – произвольная, принадлежащая плоскости 0ху | |
Произвольная плоская (в плоскости 0ху)  | 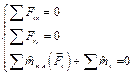 т. А – произвольная, принадлежащая плоскости 0ху т. А – произвольная, принадлежащая плоскости 0ху |
Продолжение таблицы 6.2
Система пар в плоскости 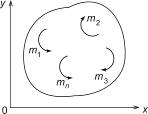 | 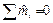 |
Сходящаяся пространственная 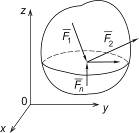 | 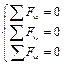 |
Параллельная пространственная ( 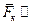 оси 0z) оси 0z) 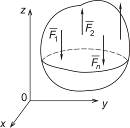 | 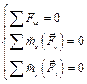 |
Продолжение таблицы 6.2
Произвольная пространственная 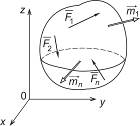 | 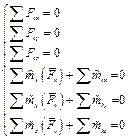 |
Система пар в пространстве 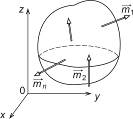 | 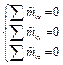 |
Вопросы для самоконтроля по теме 6
1. Как найти момент силы относительно оси?
2. Какая зависимость существует между моментом силы относительно точки и моментом этой же силы относительно оси, которая проходит через эту точку?
3. В каких случаях момент силы относительно оси равен нулю? А когда он наибольший?
4. В каких случаях система сил приводится к равнодействующей?
5. В каком случае пространственная система сил приводится:
– к динамическому винту?
6. Что называется инвариантом статики? Какие Вы знаете инварианты статики?
7. Запишите уравнения равновесия произвольной пространственной системы сил.
8. Сформулируйте необходимое и достаточное условие равновесия параллельной пространственной системы сил.
9. Изменится ли главный вектор системы сил при изменении центра приведения? А главный момент?
Тема 7. ФЕРМЫ. ОПРЕДЕЛЕНИЕ УСИЛИЙ
- Техническая механика
- Пространственная система сил
- Пространственная система сходящихся сил
- Разложение силы по трем осям координат
- Аналитический способ определения равнодействующей пространственной системы сходящихся сил
- Аналитические условия равновесия пространственной системы сходящихся сил
- Момент силы относительно оси
- Аналитические условия равновесия пространственной системы произвольно расположенных сил
- Теорема о моменте равнодействующей относительно оси (теорема Вариньона)
- iSopromat.ru
- Формы условий равновесия
- Первая форма
- Вторая форма
- Третья форма
- Другие условия равновесия
- 🌟 Видео
Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Техническая механика
Видео:5.6. Равновесие произвольной пространственной системы силСкачать

Пространственная система сил
Пространственная система сходящихся сил
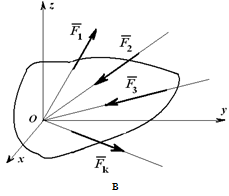
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .
Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.
Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Пусть дана пространственная система n сходящихся сил (F1, F2, F3. Fn) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .
Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.
Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.
Разложение силы по трем осям координат
Пусть дана сила F (см. рисунок 1) .

Достроим полученное изображение до параллелепипеда, у которого составляющие Fx , Fy и Fz являются ребрами, а сила F – диагональю.
Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .
Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие Fx , Fy и Fz равны по модулю проекциям силы F на эти оси.
Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы: F = √(Fx 2 + Fy 2 + Fz 2 ) (здесь и далее √ — знак корня) ;
направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .
Аналитический способ определения равнодействующей пространственной системы сходящихся сил
Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.
Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:
Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.
Аналитические условия равновесия пространственной системы сходящихся сил
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
ΣX = 0; ΣY = 0; ΣZ = 0 .
Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.
Момент силы относительно оси
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.
Разложим силу F на три взаимно-перпендикулярные составляющие F1 , F2 и F3 .
Составляющую F1 назовем окружной силой , составляющую F2 – осевой силой , а составляющую F3 – радиальной силой .
Из рисунка видно, что составляющая F1 вызывает вращательное действие, которое измеряется произведением силы F1 на радиус колеса r ; составляющая F2 стремится сдвинуть червячное колесо вдоль оси, а составляющая F3 стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F2 и F3 относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F1 , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).
Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:
Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.
Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.
Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):
- если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила FZ) ;
- если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F3 на рисунке 2) .
Аналитические условия равновесия пространственной системы произвольно расположенных сил
Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.
Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.
Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.
Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:
- ΣX = 0; ΣMx(Fi) = 0;
- ΣY = 0; ΣMy(Fi) = 0;
- ΣZ = 0; ΣMz(Fi) = 0.
Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.
Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.
Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.
Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)
Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил FΣ (см. рисунок 4) :
Приложим к телу другую систему сил, равнодействующая которой F’Σ по модулю равна FΣ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:
Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например
Запишем это условие для обеих систем:
Так как правые части этих равенств равны, то будут равны и левые :
Сократив общее слагаемое Mx(F’Σ) , получим:
Видео:Термех. Статика. Равновесие пространственной системы силСкачать

iSopromat.ru
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
Видео:Определение опорных реакции в пространственной конструкции. ТермехСкачать

Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Видео:5.7. Равновесие системы тел под действием пространственной системы сил (2 из 2)Скачать

Другие условия равновесия
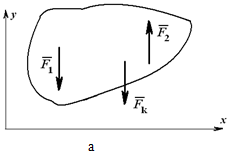
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
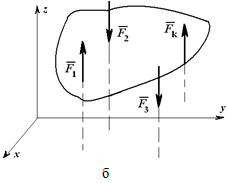
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
и два уравнения для плоской системы:
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
🌟 Видео
Условия равновесия систем силСкачать

Термех. Статика. Равновесие плоской произвольной системы силСкачать

Термех. Статика. Решение задач на равновесие пространственной системы телСкачать

5.7. Равновесие системы тел под действием пространственной системы сил (1 из 2)Скачать

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Статика #2Скачать

Пространственная система силСкачать

Математика это не ИсламСкачать

Равновесие полкиСкачать

Пространственная система сил. Решение задачи 6.4 из МещерскогоСкачать
1.4. Равновесие пространственной системы сходящихся силСкачать

Равновесие вала. Реакции опорСкачать

Система сходящихся силСкачать