Схема уравнения векторная и временная диаграммы для тока и напряжения

Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Определение

Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.

Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.

Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.

Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.

Видео:Векторная диаграмма токов и топографическая диаграмма напряженийСкачать

Разновидности

Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:

1. Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
2. Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.

Векторную диаграмму токов можно построить 2 разными способами:

1. Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
2. Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.

Видео:Векторная диаграмма - как она строится без чисел по схемеСкачать

Построение

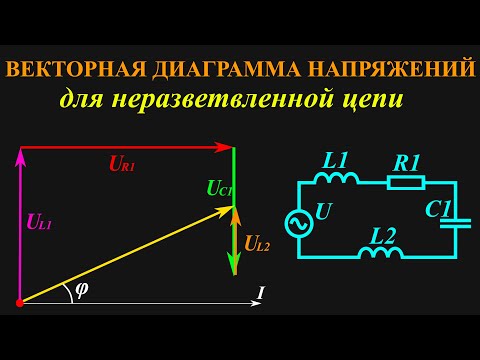
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.

1. Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
2. Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
3. Напряжение резистора UR 10 вольт, его направление совпадает с током I.
4. Сила тока в цепи I равняется 3 ампера.

Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.

1. Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
2. Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
3. Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
4. Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
5. Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.

Видео:Как построить векторную диаграмму напряжений?Скачать

Способ 2

Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:

• Резистора UR;
• Конденсатора UC;
• Катушки UL.

1. На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
2. От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
3. От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.

1. Показать результат сложения вектора UL и UC.
2. При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
3. Кроме того можно определить угол сдвига фазы φ в цепи.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.

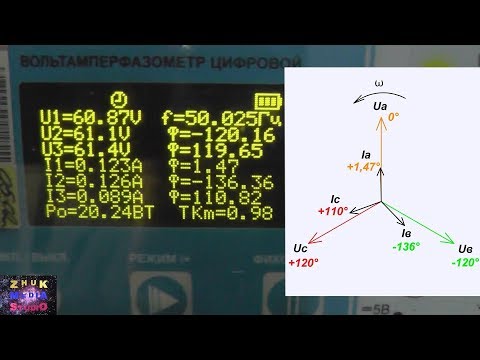
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:

1. На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
2. Угловая величина обозначается как W.
3. Также присутствует сам вектор Im и угол сдвига фаз φ.

Далее нужно сделать:

1. На плоскости выбрать точку отсчета.
2. От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
3. Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.

Видео:Построение векторной диаграммы. Цепь RLCСкачать

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Видео по теме

Видео:Векторная диаграммаСкачать

Векторная диаграмма токов и напряжений

Цифровое представление динамических процессов затрудняет восприятие, усложняет расчет выходных параметров после изменения условий на входе или в результате выполненной обработки. Векторная диаграмма токов и напряжений помогает успешно решать обозначенные задачи. Ознакомление с теорией и практическими примерами поможет освоить данную технологию.

Видео:Зачем нужны векторные диаграммы?Скачать

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Видео:Векторные диаграммы Токов и Напряжений в программе VisioСкачать

Векторные диаграммы и комплексное представление

Такой инструментарий помогает строить наглядные графические схемы колебательных процессов. Аналогичный результат обеспечивает применение комплексных числовых выражений. В этом варианте, кроме оси с действительными, применяют дополнительный координатный отрезок с мнимыми значениями. Для представления вектора пользуются формулой A*ei(wt+f0), где:

• А – длина;
• W – угловая скорость;
• f0 – начальный угол.

Значение действительной части равно A*cos*(w*t+f0). Это выражение описывает типичное гармоническое колебание с базовыми характеристиками.

Видео:Векторная диаграмма токов на комплексной плоскости вручнуюСкачать

Примеры применения

В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.

Механика, гармонический осциллятор

Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k

К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.

Свободные гармонические колебания без затухания

Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.

Гармонический осциллятор с затуханием и внешней вынуждающей силой

В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.

Расчет электрических цепей

Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.

Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).

Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.

Преобразование Фурье

Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.

Сложение двух синусоидальных колебаний

В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.

Фурье-образ прямоугольного сигнала

В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.

Дифракция

Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.

Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Построение векторной диаграммы напряжений и токов

Для изучения технологии выберем однофазный источник синусоидального напряжения (U). Ток изменяется по формуле I=Im*cos w*t. Подключенная цепь содержит последовательно подключенные компоненты со следующими значениями:

• резистор: Ur=Im*R*cos w*t;
• конденсатор: Uc=Im*Rc*cos (w*t-π/2), Rc=1/w*C;
• катушка: UL= Im*RL*cos(w*t+π/2), RL=w*L.

При прохождении по цепи переменного тока на реактивных элементах будет соответствующий сдвиг фаз. Чтобы построить вектора правильно, рассчитывают амплитуды и учитывают изменение направлений. Ниже приведена последовательность создания графики вручную.

Далее с применением элементарных правил геометрии проверяют взаимное влияние векторов.

На первом рисунке приведен результат сложения двух векторов при условии, когда Uc меньше UL. Добавив значение на сопротивление, получим результирующее напряжение Um. На третьей иллюстрации отмечен общий фазовый сдвиг.

В топографической диаграмме начало координат совмещают с так называемой точкой «нулевого потенциала». Такое решение упрощает изучение отдельных участков сложных схем.

В интернете можно найти программу для построения векторных диаграмм в режиме online.

Видео:Ошибка при подключении трансформаторов напряжения ЗНОЛ.06-10. Векторная диаграммаСкачать

Видео

Видео:Как снять векторную диаграммуСкачать

Векторные диаграммы

Видео:ТОЭ│Задача на переменный ток. Определить сопротивления элементов. Векторная диаграммаСкачать

Векторные диаграммы и комплексное представление

Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел . При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy – оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица ).

Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ₀ запишется как комплексное число

а его действительная часть

-есть гармоническое колебание с циклической частотой ω и начальной фазой φ₀.

Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.

• Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.

• Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.

• Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) – более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.

Видео:Урок 362. Анализ вынужденных электромагнитных колебаний методом векторных диаграммСкачать

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Механика; гармонический осциллятор

• Гармонический осциллятор в механике и гармонический осциллятор любой природы формально представляют точную аналогию, поэтому рассмотрим их в одном параграфе на примере механического гармонического осциллятора.
• Применение векторных диаграмм в механике сводится в основном к случаю гармонического осциллятора (в том числе имеется в виду и случай осциллятора с линейной по скорости силой трения); впрочем, векторные диаграммы могут быть до некоторой степени полезны и для исследования нескольких осцилляторов в том числе и в пределе бесконечного их количества (для колебаний или волн в распределенных системах).
• С современной точки зрения применение векторных диаграмм к гармоническому осциллятору представляет скорее только исторический и педагогический интерес, однако тем не менее в принципе они здесь вполне применимы.
• В механике применение векторных диаграмм (обычно подразумевается их применение к одномерному осциллятору) имеет ту особенность, что добавляющаяся вторая координата для превращения колебаний во вращение может иметь не только чисто формальный абстрактный смысл, но для одномерной механической системы такого сорта может быть указана механическая же двумерная система, для которой векторная диаграмма первой реализуется как вполне реальное двумерное механическое движение, и все векторы реально двумерны (а после проецирования всех их и движения точки двумерной системы на одну ось, мы получаем мгновенные значения соответствующих величин – в том числе положения – для соответствующей одномерной системы); таким образом, для механической одномерной системы возможна не только формальная математическая, но и реальная механическая модель, переводящая колебательное одномерное движение во вращательное движение в двумерном пространстве, реализующая в себе векторную диаграмму для одномерной системы.

Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.

Представление синусоидальных функций в виде комплексных чисел

Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.

Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции

Данный синусоидальный сигнал можно представить в виде комплексной величины

Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.

Векторная диаграмма при последовательном соединении элементов

Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.

Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.

Рис. 1. Последовательное соединение элементов цепи

Составим уравнение для данной цепи по второму закону Кирхгофа :

По закону Ома падение напряжений на элементах определяется по следующим выражениям:

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.

Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.

При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.

Падение напряжения на резисторе U_R совпадает по направлению с током I (т.к. U_R = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. U_L = I ∙ jX_L, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. U_C = −I ∙ jX_C, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи

Векторная диаграмма при параллельном соединении элементов

Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

Рис. 3. Параллельное соединение элементов цепи

Составим уравнение для данной цепи по первому закону Кирхгофа :

Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.

При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.

Ток в резисторе I_R совпадает по направлению с ЭДС E (т.к. I_R = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. I_L = −j ∙ E / X_L, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. I_C = j ∙ E / X_C, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи

Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.

Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.

Видео:Векторные диаграммы ЭДС, токов и напряженийСкачать

Алгоритм создания лучевой векторной диаграммы в Excel

Чтобы упростить наш урок, давайте предположим, что мы говорим об отношениях не между четырнадцатью как на графике, а пока только с 4-ма людьми по имени Антон, Алиса, Борис и Белла.

Наша матрица уровня отношений и связей между ними выглядит следующим образом:

• 0 значит отсутствие отношений;
• 1 означает слабые отношения (например: Антон и Алиса просто знают друг друга);
• 2 означает крепкие отношения (например, Борис и Алиса друзья).

Как можно геометрически смоделировать визуализацию этих исходных данных? Если бы мы нарисовали отношения между этими четырьмя людьми (Антон, Алиса, Борис и Белла), это схематически выглядело бы так:

2 критерия, которые нам нужно определить:

1. Расположение точек (где печатаются имена людей).
2. Линии (начальная и конечная точка соединения линий).

Определение и построение точек

Сначала нам нужно построить наши точки таким образом, чтобы промежуток между каждой точкой был одинаковым. Это создаст сбалансированный график.

Какая геометрическая фигура максимально удовлетворяет нашу потребность в таких равных промежутках? Конечно же круг!

Вы можете возразить, что на готовой модели диаграммы нет фигуры круга. Да действительно нет –вот так. Нам не нужно рисовать круг. Нам просто нужно построить точки вокруг него.

Таким образом, у нас есть 4 заинтересованные стороны, нам нужно 4 точки:

1. Если у нас 12 заинтересованных сторон, нам нужно 12 точек.
2. Если у нас есть 20, нам нужно 20 точек.

Предполагая, что источником нашего круга является (x, y), радиус – это r, а тета – 360, деленная на количество нужных нам точек. Первая точка (x1, y1) на окружности будет в этой позиции:

• x1 = x + r * COS (тета);
• y1 = y + r * SIN (тета).

Как только все точки рассчитаны и подключены к XY-диаграмме (точечная диаграмма), давайте двигаться дальше.

Построение линий на лучевой диаграмме

Допустим, у нас в сети есть n человек. Это означает, что каждый человек может иметь максимум n -1 отношений.

Таким образом, общее количество возможных линий на нашем графике равно n * ( n -1) / 2.

Нам нужно разделить его на 2, как будто A знает B, тогда B тоже знает A. Но нам нужно нарисовать только 1 линию.

Шаблон лучевой диаграммы для анализа сетевого графика настроен для работы с 20 людьми. Его можно скачать в конце статьи и использовать как готовый аналитический инструмент визуализации данных связей. Это означает, что максимальное количество строк, которое мы можем иметь, будет равно 190.

Каждая строка требует добавления отдельной серии на график. Это означает, что нам нужно добавить 190 серий данных только для 20 человек. И это удовлетворяет только одному типу линии (пунктирная или толстая). Если нам нужны разные линии в зависимости от типа отношений, нам нужно добавить еще 190 серий.

Это больно и смешно одновременно. К счастью, выход есть!

Мы можем использовать гораздо меньшее количество серий и по-прежнему строить один и тот же график.

Допустим, у нас есть 4 человека – A,B,C и D. Ради простоты, давайте предположим, что координаты этих 4-х участников следующие:

И скажем, A имеет отношения с B, C и D.

Это означает, что нам нужно нарисовать 3 линии, от A до B, от A до C и A до D.

Теперь, вместо того, чтобы поставить 3 серии для диаграммы, что если мы поставим одну длинную серию, которая выглядит следующим образом:

Это означает, что мы просто рисуем одну длинную линию от A до B, от A до C, от A до D. Договорились, что это не прямая линия, но точечные диаграммы Excel могут нарисовать любую линию, если вы предоставите ей набор координат.

Смотрите эту иллюстрацию, чтобы понять технику:

Таким образом, вместо 190 рядов данных для диаграммы нам просто нужно 20 рядов.

На последнем графике мы имеем 40 + 2 + 1 ряд данных. Это потому что:

• 20 линий для слабых отношений (пунктирные линии);
• 20 линий для прочных отношений (толстые линии);
• 1 строка для выделения синим цветом слабых отношений выделенного участника;
• 1 строка для выделения зеленым цветом сильных отношений выделенного участника;
• 1 комплект без линий, а просто точек для подписей данных на графике.

Как сгенерировать все 20 серий данных:

Это требует следующей логики:

Для каждого четного ряда:

• разделите номер строки на 2, чтобы получить номер человека (скажем, m );
• ( Xn, Yn ), если нет отношений между n и m ;
• ( Xm, Ym ), если есть отношения.

Нам нужны формулы MOD и INDEX для выражения этой логики в Excel.

Как только все координаты линии будут рассчитаны, добавьте их к нашему точечному графику как новые ряды используя инструмент из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления всех 43-х рядов.

Реализовывать создание такой лучевой диаграммы связей будем в 3 этапа:

1. Подготовка исходных данных.
2. Обработка данных.
3. Визуализация.

Видео:Переменный ток. По векторной диаграмме представить схему цепи. Найти входное напряжение и мощностиСкачать

Подготовка данных для лучевой диаграммы

Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:

На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:

С подготовкой данных мы закончили переходим к обработке.

Как вычислить сумму векторов?

Вектора и матрицы в электронной таблице хранятся в виде массивов.

Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:

Для вычисления суммы векторов нужно выполнить следующую последовательность действий:

– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.

– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.

– Ввести в выделенный диапазон формулу перемножения диапазонов

– Нажать комбинацию клавиш [Ctrl] + [Shift] +[Enter].

Даны два вектора:

Требуется вычислить сумму этих векторов.

– В ячейки диапазона А2:A4 введем значения координат вектора a1, а в ячейки диапазона С2:С4 – координаты вектора a2.

– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С ( E2:E4 ) и введем в выделенный диапазон формулу:

– Нажмем комбинацию клавиш [Ctrl] + [Shift] +[Enter]. В ячейках диапазона E2:E4 будут вычислены соответствующие координаты результирующего вектора.

Видео:Двухфазное КЗ на векторных диаграммахСкачать

Сложение и вычитание векторов

Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:

Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.

Вектор I_m, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).

Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.

🎬 Видео

метод векторных диаграммСкачать

Резонанс напряжений в электрической цепиСкачать